一类含有p-Laplacian算子的半正分数阶微分方程脉冲边值问题正解的存在性
褚丽敏, 胡卫敏, 苏有慧
(1.伊犁师范大学 数学与统计学院,新疆 伊犁 835000; 2.徐州工程学院 数学与统计学院,江苏 徐州 221018;3.伊犁师范大学 应用数学研究所,新疆 伊犁 835000)
分数阶微分方程边值问题是微分方程理论的重要分支. 脉冲微分方程能够充分考虑到突变对状态的影响, 所以具有脉冲条件的分数阶微分方程解的存在性引起了许多学者的关注[1-2]. 特别是最近几年,有学者致力于研究具有p-Laplacian算子的分数阶微分方程的脉冲边值解的存在性, 并取得了一些研究成果[3-7].例如,文献[7]中研究了一类具有p-Laplacian算子的分数阶微分方程积分边值问题多重正解的存在性:
其中1 然而,文献[7]中没有研究带有脉冲边值条件的半正分数阶微分方程,文献[8]中没有研究具有p-Laplacian算子的半正分数阶微分方程. 当方程的非线性项可以取负值时, 研究的边值问题称为半正问题[9]. 半正问题在应用数学和物理等领域具有广泛的应用, 如机械系统的屈曲、悬索桥的设计、 化学反应和自然资源管理等[10]. 近十几年, 很多文献研究了半正问题正解的存在性,而研究具有p-Laplacian算子且带有脉冲边值条件的半正分数阶微分方程具有一定难度. 受文献[7-8]启发, 本文研究具p-Laplacian算子的半正分数阶微分方程脉冲边值问题正解的存在性: 在这一节, 我们给出一些定义、相关引理及边值问题(1)的Green函数. PC(J,R)= {u:J→R|u∈C(Jk),k=0,1,…,m}, PC1(J,R)= {u:J→R|u∈C1(Jk),k=0,1,…,m}, 其范数定义为 定义1[11]令α>0, 函数f:[0,+∞)→R的分数阶积分定义为 其中右边是在[0,+∞)逐点定义的. 定义2[11]令α>0, 函数f:[0,+∞)→R的分数阶微分定义为 引理2[13]设E是Banach空间,T:E→E是全连续算子,且V={u∈E|u=μTu,0<μ<1}有界,则T在E有一个不动点. 引理4若1<α≤2,则分数阶微分方程边值问题 (2) 的解是 其中 G(t,s)= 证明由引理1知, 当t∈J0时, 存在常数c0,c1∈R, 使得 c0+c1t, (3) (4) 当t∈J1时,存在常数d0,d1∈R,使得 d0+d1(t-t1), 从而 c0+c1t1, c0+c1t1+I1(u(t1)), c1+Q1(u(t1)). 因此 (t-t1)Q1(u(t1))+c0+c1(2t-t1),t∈J1. 同理可知, 当t∈Jk,k=1,2,…,m时, 有 (5) 由边值条件u(0)=u′(1)=0, 得 c0=0, 将c0,c1代入(3)式和(5)式可得(6)式(见附录),其中k=1,2,…,m. 在这一节, 我们利用不动点定理得到边值问题(1)正解的存在性结论. 定义算子T:PC(J,R)→PC(J,R)如下: 把研究问题(1)解的存在性转化成研究算子T不动点的存在性. 引理5算子T:PC(J,R)→PC(J,R)是全连续的. |(Tu)(t2)-(Tu)(t1)|≤ 故T在Jk上是等度连续的, 其中k=1,2,…,m.由Arzela-Ascoli定理知算子T是全连续的. 定理1假设存在正数Li>0(i=1,2,3), 使得|φq(f(t,u,u′))|≤L1,|Ik(u)|≤L2,|Qk(u)|≤L3,k=1,2,…,m,则对于任意u∈Ω,t∈J,问题(1)至少存在一个正解. (10) 定理3设存在正数Ki>0(i=1,2,3),使得 |φq(f(t,u(t),u′(t)))-φq(f(t,v(t),v′(t)))|≤ K1|u-v|,|Ik(u)-Ik(v)|≤K2|u-v|,|Qk(u)-Qk(v)|≤K3|u-v|, 其中t∈J,u,v∈C([0,1],R),k=1,2,…,m.若 则问题(1)有唯一解. 在这一节, 举例验证本文得到的结论. 例1考虑非线性分数阶微分方程边值问题: (12) 证明 再取δi(i=1,2,3)满足(10)式,即 由定理2可知问题(12)至少有一个正解. 附录: (6) (7) (8) (9) (11)
1 预备知识
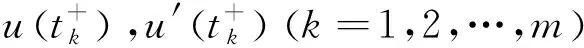
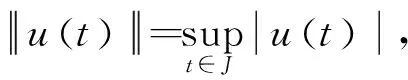
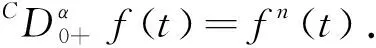
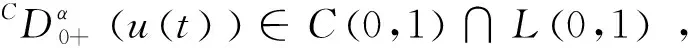
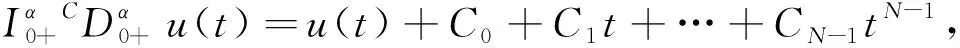




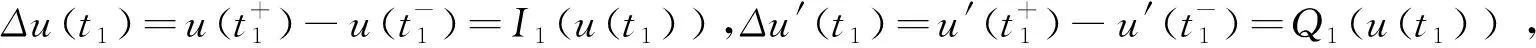
2 主要结果
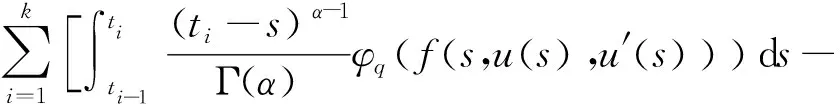
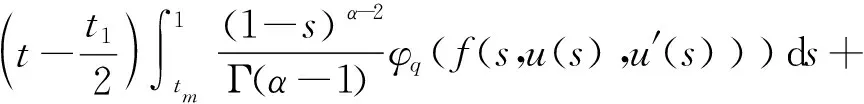
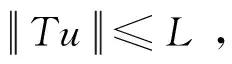
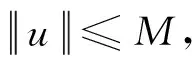


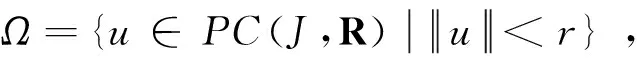


3 应用举例