制造业企业参与工业互联网平台行为策略的演化博弈分析
郭俊一, 吴丽娜, 张雪飞
(1.广州华商学院 管理学院, 广州 511300; 2.广州商学院 管理学院, 广州 510700)
当前,中国制造业正处于转型升级的关键时期,所面临的机遇和挑战并存。大多数制造业企业尚未实现云端化,生产、研发、财务、管理等环节的信息系统尚未打通。很多制造业企业发展观念落后,对企业生产运营数据的平台化尚存在着“是否能为企业带来好处”的疑虑和“企业商业数据是否安全”的担忧。
国内外学者对制造业企业参与工业互联网平台行为方面的研究主要集中在3个方面。一是工业互联网平台在发展过程中面临的问题与挑战研究,如Ma等[1]、Yin等[2]、李君等[3]、张梦琳[4]的研究;二是工业互联网对制造业的影响机制研究,如Wang等[5];三是用户参与平台组织的动力机制以及吸引用户参与行为意愿的影响因素研究,如Hsieh等[6]。本文基于动态演化的博弈理论,从系统的角度分析制造业企业接入工业互联网平台情况的行为策略选择,即研究在第三方政府扶持的视角下,工业互联网平台以及制造业企业在整个博弈过程中的竞合关系,深入分析工业互联网平台与制造业企业博弈过程中的损益关系及其行为策略趋于稳定的条件,利用MATLAB软件仿真分析重要的决策变量对三方交互行为的影响,分析多主体参与博弈过程的演化策略,据此提出激励制造业企业参与平台行为的政策建议,着眼于现有研究缺乏的领域。
1 多主体参与下的制造业企业参与平台行为的博弈模型构建
1.1 模型构建
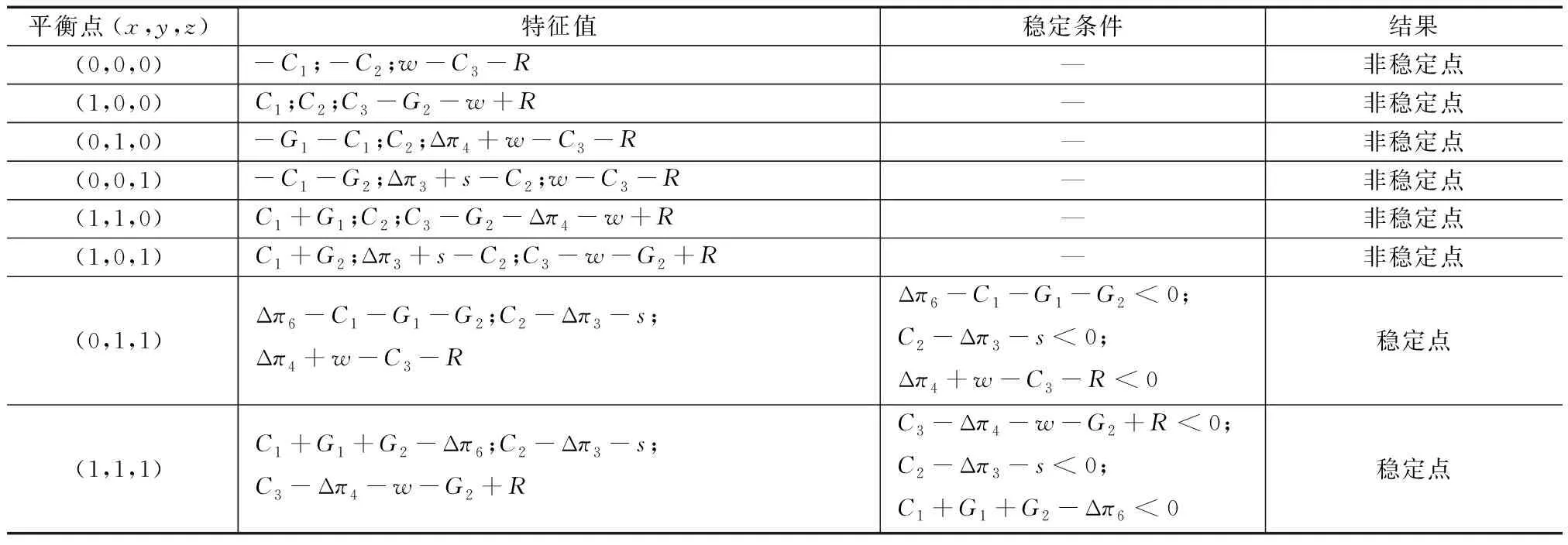
假设政府、工业互联网平台及制造业企业分别是博弈方1、博弈方2以及博弈方3。三方均为有限理性且具有学习模仿能力的主体,能通过对比其他主体收益策略来调整自身策略以达到最优。博弈方1即政府,政府对于工业互联网平台和制造业企业实行的策略有两种,即采取“扶持”策略和“不扶持”策略。博弈方2即工业互联网平台。在博弈过程中,工业互联网平台可以作出决策有两种,即采取“赞助”策略和采取“不赞助”策略。对于博弈方3即制造业企业而言,其作出的决策有两种,即采取“接入”策略和采取“不接入”策略。根据表1中设置的变量和模型假设,并且设定0 表1 变量符号及定义 根据三方主体博弈树模型,得出政府、工业互联网平台和制造业企业的收益矩阵,见表2。在表2中,三方主体之间共有8种策略组合,分别是:(扶持、赞助、接入)、(不扶持、赞助、接入)、(扶持、赞助、不接入)、(不扶持、赞助、不接入)、(扶持、不赞助、接入)、(不扶持、不赞助、接入)、(扶持、不赞助、不接入)、(不扶持、不赞助、不接入)。收益矩阵的排序从上到下分别是政府、工业互联网、制造业企业。 表2 政府、工业互联网平台和制造业企业的收益矩阵 根据表2的收益矩阵,可得政府、互联网平台服务商以及制造业企业三方主体的期望收益。 2.1.1 政府的期望收益 E11=yz(π5+Δπ6-G1-G2-C1)+ y(1-z)(-G1-C1)+(1-y)z(π5-G2-C1)+ (1-y)(1-z)(-C1)=yzΔπ6+zπ5-zG2- yG1-C1 (1) E12=yzπ5+(1-y)zπ5=zπ5 (2) (3) 2.1.2 工业互联网平台的期望收益 E21=xz(π1+Δπ3+Δπ′3+G1-C2-C′2)+ (1-x)z(π1-C2-C′2)+x(1-z)(Δπ′3+G1- C′2-C2)+(1-x)(1-z)(-C′2-C2)= zπ1+zΔπ3+xΔπ′3+xG1-C2-C′2 (4) E22=xz(π1+Δπ′3+G1-C′2-S)+ (1-x)z(π1-C′2-S)+x(1-z)(Δπ′3+ G1-C′2)+(1-x)(1-z)(-C′2)= zπ1+xΔπ′3-C′2-zS+xG1 (5) (6) 2.1.3 制造业企业的期望收益 E31=xy(π2+Δπ4+G2-C3-C′3-R)+ (1-x)y(π2+Δπ4-C3-C′3-R)+ x(1-y)(π2+G2-C3-C′3-R)+ (1-x)(1-y)(π2-C3-C′3-R)= yΔπ4+xG2+π2-C3-C′3-R (7) E32=xy(π2-C′3-w)+(1-x)y(π2- C′3-w)+x(1-y)(π2-C′3-w)+ (1-x)(1-y)(π2-C′3-w)= π2-w-C′3 (8) (9) 由此可得出描述两主体之间博弈过程的微分方程F(x)、F(y)、F(z): x(1-x)(yzΔπ6-zG2-yG1-C1) (10) E22)=y(1-y)(zΔπ3-C2+zS) (11) E32)=z(1-z)(yΔπ4+xG2+w-C3-R) (12) (13) 解之可得 (14) 2.2.1 政府的复制动态分析 政府在不同情况下的演化博弈动态趋势如图1所示。 图1 政府在不同情况下的演化博弈动态趋势 从以上分析可看出,当政府采取“扶持”策略所获得的收益小于其扶持成本时,政府选择“不扶持”策略,而当政府采取“扶持”策略所获得的收益大于其扶持成本,且工业互联网平台选择“赞助”策略的概率大于某一值时,政府则选择“扶持”策略。该结果表明政府对“扶持”策略的选择与否,与其获得的利益息息相关,并且工业互联网平台的决策对于整个系统的稳定起着重要的作用。 2.2.2 工业互联网平台的复制动态分析 工业互联网平台在不同情况下的演化博弈动态趋势如图2所示。 图2 工业互联网平台在不同情况下的演化博弈动态趋势 从以上的分析可知,当工业互联网平台选择“赞助”策略时的收益大于工业互联网平台所投入的成本和机会损失之和时,工业互联网平台将选择“赞助”策略,而其选择“赞助”策略时的收益小于工业互联网平台所投入的成本和机会损失之和时,工业互联网平台将选择“不赞助”策略。 2.2.3 制造业企业的复制动态分析 制造业企业在不同情况下的演化博弈动态趋势如图3所示。 图3 制造业企业在不同情况下的演化博弈动态趋势 从以上分析可知,当制造业企业接入工业互联网平台所获得的收益大于接入的成本和机会损失之和时,制造业企业将选择“接入”策略。然而,当制造业企业接入平台所获收益小于接入的成本与机会损失之和,且政府选择“扶持”策略的概率大于某一值时,制造业企业仍然会选择“接入”策略,表明制造业企业选择接入工业互联网与否,和政府与工业互联网平台采取策略的选择密切相关。 2.2.4 演化博弈均衡的演化稳定策略分析 采用雅克比矩阵的局部稳定性分析法可以求解出政府、工业互联网平台以及制造业企业三方演化的平衡点。分别对F(x)、F(y)和F(z)求x、y和z的偏导,即可得雅克比矩阵Q,即 (15) 该矩阵的稳定性将通过对雅克比矩阵行列式的值是否大于0和矩阵的迹是否小于0,即detQ>0且trQ<0这两个原则来判定。其中,稳定性条件表示为 detQ=a11(a22a33-a23a32)+a12(a23-a21)+ a13(a21a32-a22a31)=a11(a22a33-a23a32)+ a31(a12a23-a13a22)>0 (16) trQ=a11+a22+a33<0 (17) 从以上分析可知,该系统演化博弈均衡的渐进稳定性将遵从8个定理,见表3。 表3 政府、工业互联网平台、制造业企业演化均衡点的稳定性定理 由表3分析易知,在政府、工业互联网平台、制造业企业演化博弈系统中,存在(0,1,1)和(1,1,1)两种演化的稳定策略。①满足Δπ6-C1-G1-G2<0,C2-Δπ3-s<0以及Δπ4+w-C3-R<0时,均衡点(0,1,1)是演化均衡策略。即制造业企业接入工业互联网平台的风险损失与制造业企业接入工业互联网平台的成本小于其选择“接入”策略时的收益与不接入时的机会损失、互联网平台服务商采取赞助的收益大于其采取赞助措施的成本与其选择不赞助策略时机会损失之和。双方将选择赞助、“接入”策略,而此时由于政府采取“扶持”策略的收益小于其扶持所付出的成本,政府选择 “不扶持”策略。在此均衡稳定状态下,政府未采取“扶持”策略,但理性的制造业企业仍然选择“接入”策略。虽然此时整个供应链系统的可以获得暂时的稳定与发展,但是当前的均衡在实际运行过程中很难达到。②满足C3-Δπ4-w-G2+R<0,C2-Δπ3-s<0以及C1+G1+G2-Δπ6<0时,均衡点(1,1,1)为演化均衡策略。即政府的扶持成本小于其扶持所获收益,工业互联网平台选择“赞助”策略的收益大于所付出的成本,制造业企业选择“接入”工业互联网平台所获得收益大于其所附出的成本和风险损失时,政府趋于选择“扶持”策略、工业互联网平台趋于选择“赞助”策略、制造业企业趋于选择“接入”策略。该策略为理想的稳定性策略,有利于供应链系统的健康发展。 根据复制动态方程及约束条件,运用MATLAB软件模拟仿真“政府-工业互联网平台-制造业企业”在上述8种情形下趋于(1,1,1)最优均衡时,重要参数变化对三方演化结果的影响。设初始时间为0,演化结束时间为50,Δπ6=0.9,G1=0.2,G2=0.2,Δπ3=0.5,Δπ4=0.8,C1=0.12,C2=0.2,C3=0.15,s=0.2,R=0.15,w=0.25。进一步分析附加收益、机会损失和风险损失对系统稳定性的影响。 2.3.1 附加收益对制造业企业策略选择的影响 在其他参数不变的情况下,调整制造业企业选择“接入”策略的附加收益Δπ4的取值,分析该因素对制造业企业策略选择的影响,如图4所示。在Δπ4=0.1时,制造业企业的演化策略逐渐趋向于0,逐渐增大Δπ4的取值后,制造业企业将选择“接入”策略。由此可知,附加收益Δπ4对制造业企业的策略选择的影响显著,并且Δπ4的值越大,制造业企业选择“接入”策略的收敛速度越大。 图4 附加收益对制造业企业选择策略的影响趋势 2.3.2 机会损失对制造业企业策略选择的影响 在其他参数不变的情况下,调整制造业企业选择“不接入”策略的机会损失w的取值,分析该因素对制造业企业策略选择的影响,如图5所示。随着w取值的不断增大,制造业企业的演化策略趋向于1的收敛速度逐渐加快。可见,机会损失w对制造业企业的策略选择有影响作用,表明当制造业企业的策略选择与其“不接入”工业互联网平台的机会损失密切相关。 图5 机会损失w对制造业企业策略选择的影响趋势 2.3.3 风险损失对制造业企业策略选择的影响 在其他参数不变的情况下,调整制造业企业选择“接入”策略的风险损失R的取值,分析该因素对制造业企业策略选择的影响,如图6所示。在R=0.1时,制造业企业的演化策略逐渐趋向于0,逐渐增大R的取值后,制造业企业将选择“接入”策略。由此可知,风险损失R对制造业企业的策略选择的影响显著,并且R的值越小,制造业企业选择“接入”策略的收敛速度越大,表明当制造业企业是否选择“接入”策略,与其获得承担的风险损失密切相关。 图6 风险损失R对制造业企业策略选择的影响趋势 基于演化博弈理论构建政府、工业互联网平台以及制造业企业的三方博弈模型,分析多主体之间的博弈行为策略。通过讨论复制动态系统中存在的稳定点以及在该点处博弈系统的演化稳定条件,最后通过MATLAB软件仿真分析主要决策变量对系统稳定性的影响。研究结果表明:“政府-工业互联网平台-制造业企业”演化系统中各主体之间相互牵制、相互影响;选择“接入”策略的附加收益、风险损失,以及选择“不接入策略”的机会损失是影响制造业企业行为策略的影响因素。 基于以上研究结论,针对制造业企业“接入”工业互联网平台的行为策略选择问题,提出以下建议: 1)政府部门作为最广泛利益的代表,应及时明确在市场中的“阶段性托管”角色,确立在市场中的“主人翁”地位,改变管理思维、创新管理手段,以最大程度实现公共利益。 2)在上述中演化博弈模型中,工业互联网平台选择“赞助”策略所获得的收益对博弈系统的稳定尤为重要。因此,工业互联网平台注重提高新技术的投资,提高系统的反应速度,建立公开透明的历史评价体系,使得线上单次交易变成重复多次博弈,激发制造业企业参与的主动性积极性的同时,提高持续参与的热情,工业互联网平台应切实建立有效的用户关系管理机制。 3)开放、分享的组织文化才具有更大的包容性和创造性,制造业企业应树立“上平台”意识,加深对工业互联网的认识,建立“共享、共创”的组织文化,增强知识学习的能力,提升运用工业互联网新技术、新工具、新模式的能力和信心,加大参与的力度,共享数据资源,积极参与并建设平台经济,以提高价值创造的能力。
1.2 收益矩阵的构建

2 多主体参与下的制造业企业参与平台行为策略演化均衡分析
2.1 收益期望函数构建









2.2 三方演化均衡策略分析





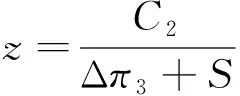
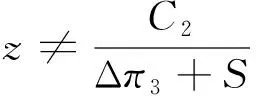


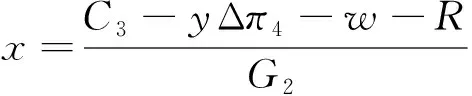
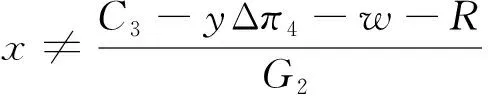

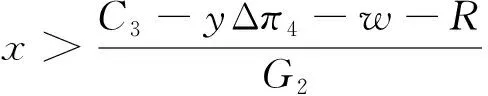



2.3 模拟仿真分析



3 结论与建议

