一道有关积分中值定理的全国大学生数学竞赛试题的探讨

刘鑫旺， 沈 艳

(哈尔滨工程大学 数学科学学院，哈尔滨 150001)

1 引 言

关于中值定理的证明问题，无论是借助微分中值定理，还是积分中值定理[1-5]，其辅助函数或者相关积分恒等式的构造，对于学生而言都是较为头疼的问题.对于全国大学生数学竞赛而言，近年来也出现了一些中值定理相关问题，命题组给出的参考答案虽然构造巧妙，但学生很难想到.学生面对类似的问题时，很难把握答案的精髓和切入点，难以灵活运用相应的构造技巧，无法做到举一反三.本文从一道全国大学生数学竞赛决赛试题引入，给出证明该类问题的一般做法，并对题目做一定的推广，体现了大学数学课堂教学中传授数学思想与数学方法的重要性[6].

2020年第11届全国大学生数学竞赛决赛(非数学类)的第四道试题为

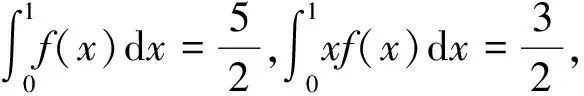
该试题的参考答案如下：

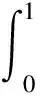
根据积分中值定理[7]，存在ξ∈(0,1)，使得ξ(1-ξ)[3-f′(ξ)]=0，即f′(ξ)=3.

2 分析与思考

2.1 引言问题的分析

从题设条件来看，由于题目已知两个定积分值，且要证明的结论含有导数，因此整体基调应当借助积分中值定理.为了出现导数值，首先采用分部积分的办法，进行等价变形，即

即

(1)

即

(2)

将两个含f′(x)的定积分，即式(1)，(2)进行线性组合，为具有一般性，有

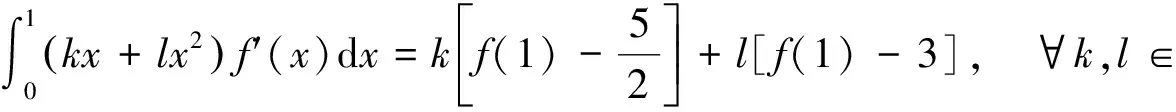
由积分第一中值定理[8]，若满足

(i)f′(x)在[0,1]上连续，

(ii)kx+lx2在[0,1]上不变号且可积，

则存在ξ∈(0,1)，使得

(3)

这里需要说明的是，原始定理内容要求ξ∈[0,1]，但借助变上限积分函数与拉格朗日中值定理，可以证明，这样的中值可以在ξ∈(0,1)取得.

此时，若给定一组(k,l)及f(1)的值，即可确定一个等式关系，在满足积分中值定理的条件下，可利用积分中值定理确定一个中值.然而，本题未给出f(1)的具体值，因此，笔者可以合理猜测，对于此题而言，需要确定一组(k,l)，使得式(3)的f(1)消失，因此，本题必有k=-l.

更一般地，当kx+lx2在[0,1]内不变号时，即x(k+lx)在[0,1]内不变号，只需满足即(k+lx)在[0,1]内不变号，即要求(k+l·0)(k+l·1)≥0，此时(k,l)的可行域如图1的阴影区域所示.

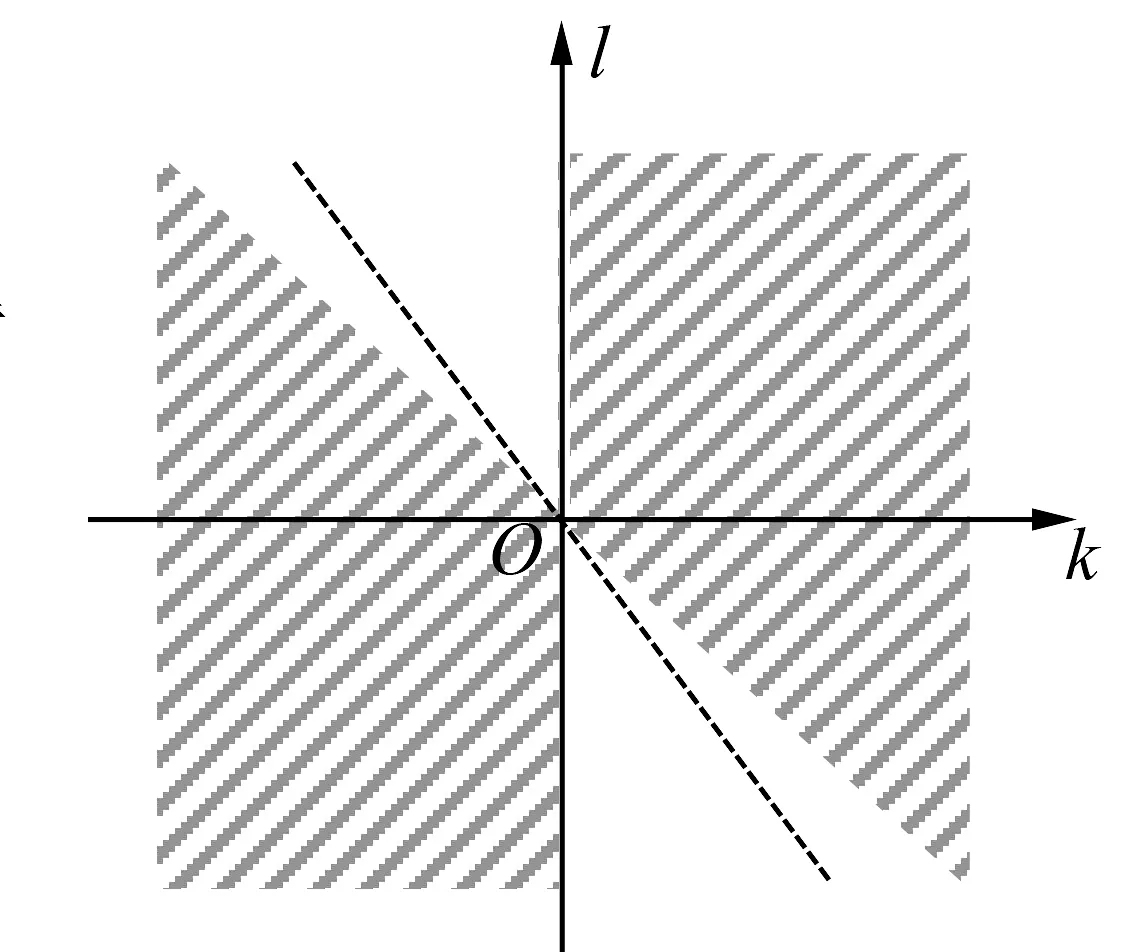
图1 (k,l)的可行域

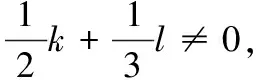
由积分中值定理，在可行域内，有

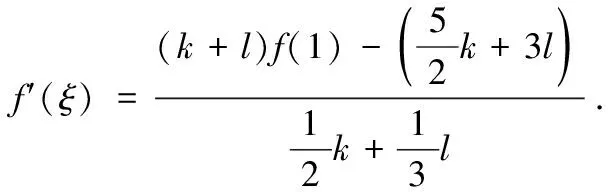
(4)

例如，题中若给出f(1)=2021，并令k=2l≠0，则从式(4)可以得到的含中值的导数值为

反之，若题目给出f(1)的值，以及要证的含中值的导数值，通过上面的方法，可以构造出一组相应的(k,l)值.

2.2 类题的推广

下面，给出另外一个例子，来说明实际命制此类问题时的过程.

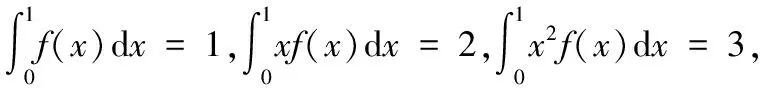
采用与上例类似的办法，首先容易得到

因此，有

进而，对于∀A,B,C∈，有

为了能够使用积分第一中值定理，需满足

(i)f′(x)在[0,1]上连续，该条显然，

(ii)x(A+Bx+Cx2)在[0,1]上不变号且可积，由于其为不超过三次的多项式，只需证g(x)=Cx2+Bx+A在[0,1]上不变号.

首先，由于题中未给出f(1)的值，因此，需要A+B+C=0，即A=-B-C.

此时，若同时满足g(x)=Cx2+Bx+A在[0,1]内不变号，则由积分中值定理，存在ξ∈(0,1)，使得

(5)

下面讨论g(x)=Cx2+Bx+A在[0,1]内不变号时，A,B,C应满足的条件：

由A=-B-C，有g(x)=Cx2+Bx+A=Cx2+Bx-(B+C).

(i)C=0.

此时，g(x)=B(x-1)为一次函数，且B≠0.

若不然，则A=B=C=0，将无法得到一个确切的含中值的导数值，因此，本文不考虑这种平凡情况.

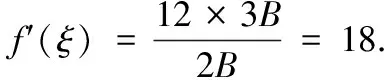
(ii)C≠0.

由二次函数的图像性质可以知道，从二次函数开口方向、截距、对称轴位置等方面考虑，为使g(x)=Cx2+Bx+A在[0,1]上不变号，有下面四种可能的情况，分别如图2所示.

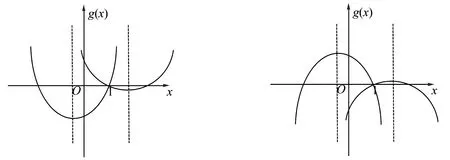
图2 二次函数的可能形状

由图2的图像可知，有下列不等式成立

即

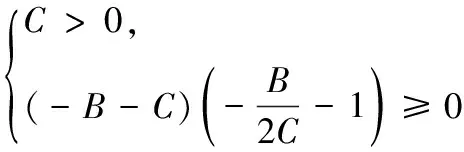
总之

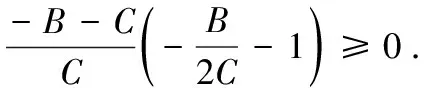
(6)

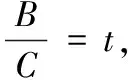
因此，当t∈(-∞,-2]∪[-1,+∞)时，使用积分中值定理，由式(5)，存在ξ∈(0,1)，使得

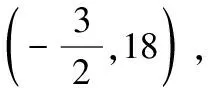
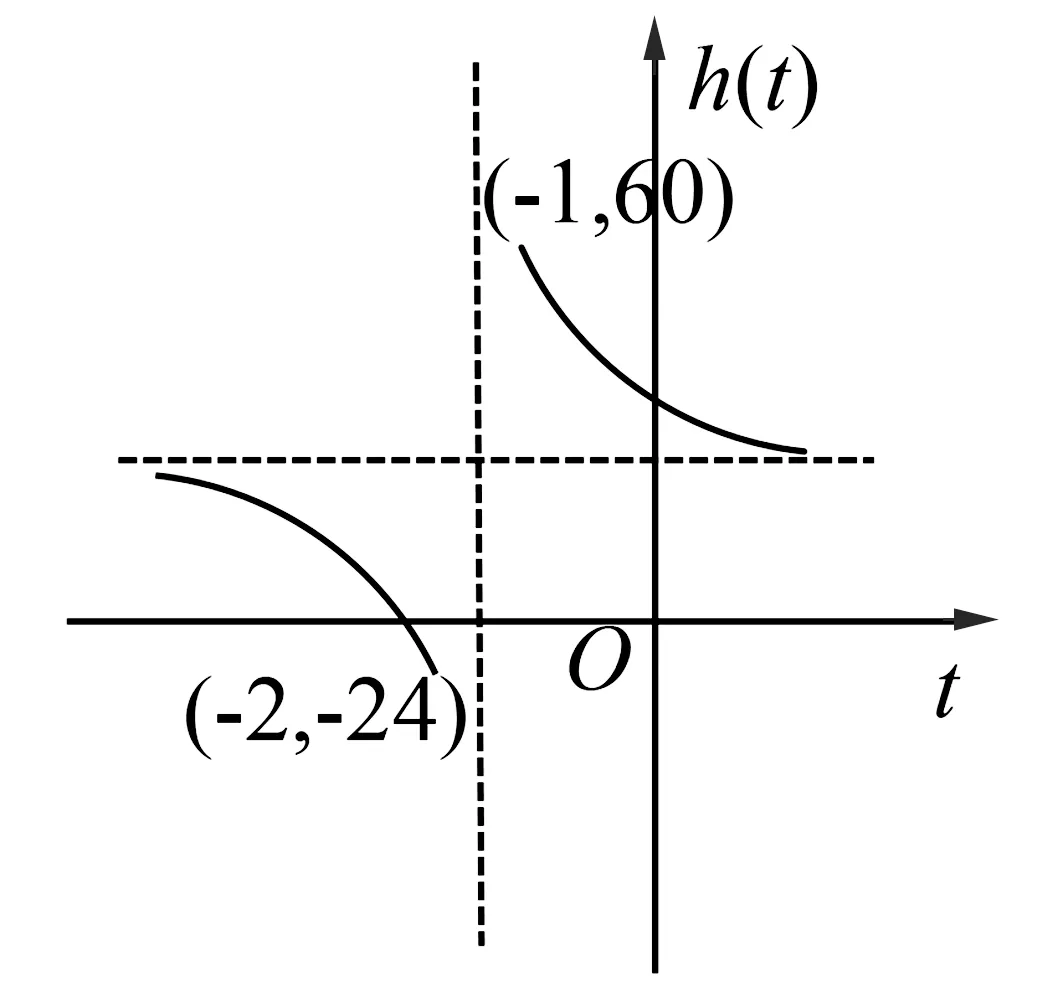
图3 函数h(t)的图像

综上，由已知条件，可以利用积分中值定理证得的f′(ξ)可能取值范围为[-24,60].

进一步，若题目给定f(1)的值，可通过上述方法，类似得到可利用积分中值定理证得的f′(ξ)的可能取值范围，留给读者思考.

3 结 论

本文给出了利用待定系数法，通过数形结合的办法分别对不等式、多项式函数等进行可行域、值域等分析，解决一类利用积分第一中值定理证明的含中值的导数问题，阐明对这类问题进行证明时的构造技巧，并进一步讨论了通过添加额外的已知条件，如函数在区间端点处的函数值时的处理思路.对于教学科研一线的教师而言，本文提供了一类问题的命制思路，实际上可以推广到含更高阶导数的问题；对于学习数学分析、高等数学，或有志于参加全国大学生数学竞赛的学生而言，遇到该类问题进行解答时，只需要根据题目中要证的导数中值，反推出一组待定系数，即可完成解答，而无需进行上述的待定系数可行域的复杂讨论.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.