基于效益耦合和时序关联特性的配电网规划项目优选模型

李文龙，张华东，于宝鑫

(国网冀北电力有限公司承德供电公司，河北 承德 067000)

随着中国经济和城市能源互联网的发展，配电网的发展逐渐复杂化，为避免生产用电和居民日常生活用电质量下降，需要对配电网进行合理的规划[1]。此外，在“城市能源互联网”这一概念提出的背景下，一定程度上电网接入电源多元化改变了配电网运行方式以及配电网运行负荷变化[2]。因此，需要重新评估电力企业供电的可靠性。基于此，配电网规划项目逐渐成为电力企业研究重点，每年国家电网公司都会花费大量支出立项研究配电网规划项目[3]。然而，配电网规划项目数量庞大，且存在一些规划范围重复的配电网规划项目，浪费电力企业资源。为此，需要优选配电网规划项目，实现配电网规划的有序性和精准性。

国内外电力企业十分重视配电网规划项目优选，可以帮助企业实现配电网规划的经济性与可靠性。目前，国内外将配电网规划项目优选分为评价排序和模型求解两类。配电网规划项目评价排序优选方法主要有层次分析法、AHP法、灰色关联度法、熵值组合法、投资效益评价法等，这类方法具有较强的主观性，评价结果不够客观[4]；模型求解类的配电网规划项目优化方法则考虑了可靠性水平、馈线迫切度、全寿命周期经济性、收益/成本分析等因素，此类方法的客观性更强，规划方案更为科学[5]。文献[6]提出了一种电网侧储能项目管理模式选择方式，结合矢量投影、灰色关联、TOPSIS这3种评价排序方法，计算项目权重，建立项目选择模型；文献[7]提出了不确定性下柔性分布式多能源发电系统扩展规划，在评估长期不确定性下运行和投资阶段的灵活性，并将其转化为随机混合整数线性规划，实现分布式多能源发电系统扩展规划；文献[8]设计了一种基于贪婪算法的城区配电网智能规划模型，采用最短路径寻优方法构建城区配电网的分布式电源接入模型，利用贪婪算法全局寻优输电路径，根据寻优结果选取更优的电网规划方案；文献[9]提出基于多策略改进的遗传算法在配电网规划中的应用，以配电网年运行费用模糊期望值最小为目标函数，融合配电网模糊潮流算法，计算配网潮流值，利用遗传算法改进整数编码方式求解配网规划模型。

以上方法对于配电网规划项目优选有一定的帮助，但均没有考虑效益耦合和时序关联特性，无法提取出项目效益耦合特性，效益参数获取不全面，使得规划投入成本高、效益不高。基于此，本文提出一种基于效益耦合和时序关联特性的配电网规划项目优选模型，建立项目效益耦合方程，提取项目效益耦合特性，设计配电网规划项目优化约束，以项目最大投资效益为目标建立优选模型。通过对现有2种方法进行对比验证，为有限预算下配电网多区域项目优选提供依据。

1 考虑效益耦合和时序关联特性的配电网规划项目优选模型

1.1 提取配电网规划项目效益耦合特性

配电网规划的单个与综合项目之间、单个与单个项目之间都存在效益耦合关系，即当配电网规划的2个或多个项目一同投入使用时，其存在效益重叠的部分，可以综合提高配电网运行可靠性；当配电网规划的2个或多个项目间存在范围重叠和功能重复时，其存在的重叠部分会降低单一项目运行效益[10]。特别是电网接入电源出现多元化的情况，各种分布式电源的接入，会导致配电网运行负荷的变化。基于此，将配电网规划项目效益耦合分为相容和扶持2种，而这2种效益耦合可以通过计算项目耦合度，确定项目效益耦合特性。

为此，将配电网规划项目记为xi(i=1,2,…,I)，其中，I表示优选配电网规划项目数量，假设配电网规划项目的序参量为ζi，配电网规划建设后的功效参数为Gi，则其效益耦合的有序功效函数为

(1)

式中f(ζi)为配电网规划项目的有序程度，当f(ζi)无线趋近于0时，配电网规划项目有序程度极低；当f(ζi)无线趋近于1时，配电网规划项目有序程度极高；+表示ζi取值为正，-表示ζi取值为负；Gmax、Gmin分别为配电网规划项目稳定临界的上限、下限。

采用线性加权的方式，集成式(1)计算得到的配电网项目序参量ζ，则有

wI≥0,∑wI=1

(2)

式中wI为配电网规划第i个项目xi相对于第j个项目xj的权重。

由式(1)、(2)可知，配电网规划项目耦合与磁链中的电感效益耦合较为相似，为此，仿照电感矩阵建立配电网规划项目效益耦合方程：

(3)

其中，O为配电网规划项目效益耦合度。O的阈值为(0,1)，则配电网规划项目效益耦合度值越接近于1，配电网规划项目效益耦合度越高。

1.2 确定配电网规划项目时序关联特性

在建设过程中，由于配电网规划项目需要按照一定的时间顺序实现配电网规划项目建设以及项目的正常运行[11]，为此，根据时序关联规则定义，确定配电网规划项目的时序关联特性。假设配电网规划项目集合I的时间序列为τ={τ1,τ2,…,τI}，将L作为项目时间序列滑动窗口长度，将I的时间序列τ离散成配电网规划项目xi和xj的时间序列τ1(xi)和τ2(xj)：

(4)

根据式(4)，给定常数a，则配电网规划项目xi和xj的时间序列τ1(xi)和τ2(xj)存在如下3种条件[12]：

(5)

式中M(τ1(xi),τ2(xj))为τ1(xi)、τ2(xj)中元素重叠次数。

当式(5)中的第1式成立时，则xi中的部分配电网规划项目包含xj中的部分配电网规划项目，因此，xi、xj具有依赖时间序列特性；当式(5)中的第2式成立时，则xi中的配电网规划项目不包含xj中的部分配电网规划项目，但是两者之间还存在紧密联系，因此，xi与xj具有互补时间序列特性；当式(5)中的第3式成立时，则xi中的配电网规划项目不包含xj中的配电网规划项目，且还相互影响，因此，xi、xj具有互斥时间序列特性。

1.3 考虑效益耦合和时序关联特性优选配电网规划项目

根据上述对配电网规划项目耦合效益和时序关联特性分析结果，设计配电网规划项目建设时间和资源、资源转移、工期、逻辑、项目依赖以及互斥和互补等约束条件，考虑电网接入电源多元化因素，约束配电网规划项目优选条件。

建设时间及建设资源：在建设过程中，配电网规划项目投入时间一定，因此需要设定项目完工时间，也称建设时间约束，即从项目建设开始，在设定的完工时间内，完成配电网规划项目建设，以此来保证配电网规划项目收益和使用。此外，配电网规划项目在建设过程中，存在多个建设阶段，每个阶段所需要的人工、设备等都存在一定的差异[13]。所以，其每个阶段所需要的建设资源都属于配电网规划项目优选的约束条件。基于此，设计配电网第i个规划项目时间约束和资源约束，其表达式为

(6)

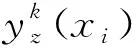
此外在规划过程中，配电网规划项目资源还存在上一阶段的资源未用完而移交到下一阶段继续使用的现象。为此，在式(6)的资源约束基础上，设计配电网规划项目建设资源转移约束：

(7)

建设工期：当xi为优选的配电网规划项目时，需要根据xi建设配电网，此时的施工周期必须处于连续施工状态。而配电网规划项目在建设过程中，优选的配电网规划项目必须符合项目实际建设步骤、建设状态，这种符合条件可以称为逻辑约束[14]。为此，设计配电网规划项目施工工期和逻辑约束，其表达式为

(8)

根据配电网规划项目所具有的时序关联特性，设计配电网规划项目的依赖、互斥、互补之间的约束关系，其约束表达式为

(9)

根据约束条件式(9)，当t时间内配电网规划项目xt,j和xt,i之间为依赖关系，且xt,i依赖xt,j，则xt,i的建设完工时间必然比xt,j的建设完工时间晚，因此，xt,i的工期大于等于xt,j的工期；当t时间内配电网规划项目xt,j和xt,i之间为互斥关系，则配电网规划项目优选只能选出一个，因此，2个项目相乘将小于等于0；当t时间内配电网规划项目xt,j和xt,i之间为互补关系，需要2个项目同时运行才能让配电网产生效益，则xt,j和xt,i的建设投入时间必须一致，因此，xt,i的工期必须等于xt,j的工期。

根据式(6)～(9)，依据配电网规划项目效益耦合和时序关联特性，以配电网规划项目最大投资效益为目标，建立优选模型：

F=max$=

(10)

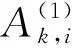
依据约束条件式(6)～(9)、优选模型式(10)得到的最大投资效益值，优选配电网规划项目。

2 算例分析

选择文献[8]中基于贪婪算法和文献[9]中基于遗传算法的项目优选模型作为此次实验对比方法，将存在多电源接入的某地区配电网规划项目作为此次实验算例，比较本文方法与文献[8]、[9]方法对该配电网规划项目的优化结果，验证本文方法研究模型的优越性。

2.1 配电网规划项目数据

实验选择的配电网规划项目规划年限均为5 a，每个项目的经济寿命周期为20 a，其规划的项目基本数据如表1所示，16个配电网规划项目的建设位置均处于该区域63 km2的市中心，16个项目在市中心需要承担30 MW/km2的负荷密度，供电质量需要达到A+。因此，3组方法优选的配电网规划项目产电比系数需要达到23.28元/(kW/h)。

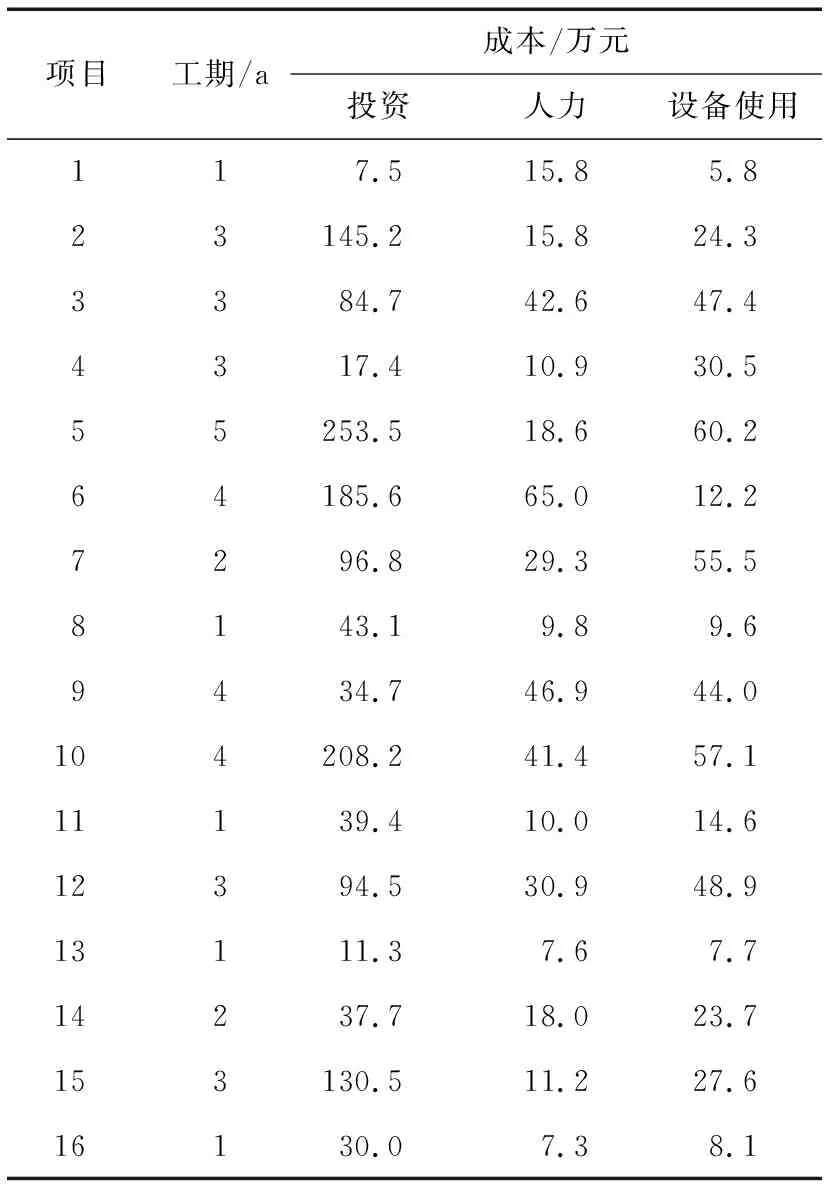
表1 配电网规划项目基本数据Table 1 Basic data of distribution network planning project

2.2 计算项目成本和效益

实验的总成本￥和效益￥l,i计算公式为

(11)

式中 ￥1为投资成本；￥2为人力成本；￥3为设备使用成本；εl为第l个供电区域产电比系数；δ为电价系数；ΔEl,i为配电网规划项目建设完成后年均减少的电量损失。

根据式(11)，计算3组项目优选模型，优选的配电网规划项目成本和效益。

2.3 算例结果

实验选择的配电网规划区域建设项目的投资成本为1 800万元，人力成本为350万元，设备使用成本为350万元。3组配电网规划项目优选模型优选的配电网规划项目成本不能超过区域设置的投资总成本。

2.3.1 配电网规划项目优选结果对比

3组配电网规划优选模型根据实验设置的项目优选条件，从表1中优选的配电网规划项目以及项目建设年份如图1所示(0表示该配电网规划项目未入选)，可以看出，基于贪婪算法的项目优选模型16项配电网规划项目均入选，且项目入选时间均为配电网规划建设的第1年；基于遗传算法的项目优选模型与本文研究模型优选配电网规划项目较为接近，但是，仅配电网规划1～7项目优选建设年份不一致。根据图1，依据表1中配电网规划项目基本数据，采用式(11)分别计算优选项目成本和效益。

图1 3组模型优选配电网规划项目对比Figure 1 Comparison of distribution network planning under three types of models

2.3.2 优选配电网规划项目成本对比

3组配电网规划项目优选模型优选项目成本对比结果如图2所示，可以看出，基于贪婪算法的项目优选模型优选的配电网规划项目，在建设配电网规划项目的5 a内，所需要的配电网规划建设成本为2 400万元；基于遗传算法的项目优选模型优选的配电网规划项目，在建设配电网规划项目的5 a内，所需要的配电网规划建设成本为1 744万元；本文研究模型优选的配电网规划项目，在建设配电网规划项目的5 a内，所需要的配电网规划建设成本为1 280万元。

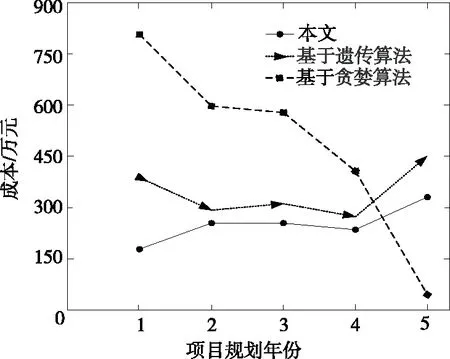
图2 优选项目成本对比Figure 2 Cost comparison of preferred projects

由此可见，3组配电网规划项目优选模型优选的配电网规划项目，均在此次建设配电网规划项目总投入成本内。但是，本文研究模型相较基于贪婪算法的项目优选模型和基于遗传算法的项目优选模型优选的配电网规划项目，所需要的配电网规划建设成本分别降低了1 120、464万元。因此，本文研究模型优选的配电网规划项目成本低。

2.3.3 优选配电网规划项目效益对比

3组配电网规划项目优选模型优选项目效益对比结果如图3所示，可以看出，基于贪婪算法的项目优选模型优选的配电网规划项目，5 a内的项目收益为4.2×104万元；基于遗传算法的项目优选模型优选的配电网规划项目，5 a内的项目收益为4.5×104万元；本文研究模型的项目优选模型优选的配电网规划项目，5 a内的项目收益为4.8×104万元，相较基于贪婪算法和基于遗传算法的项目优选模型优选的配电网规划项目，本文研究模型5 a内的项目收益分别高0.6×104、0.3×104万元。由此可见，本文研究模型优选的配电网规划项目效益高。

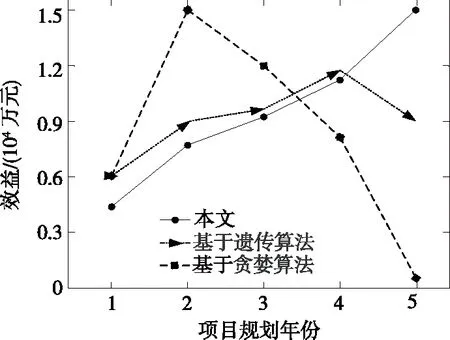
图3 优选项目效益对比Figure 3 Benefit comparison of optimized projects

3 结语

为了解决传统配电网规划方法无法得到更高效益的问题，本研究设计一种新的配电网规划项目优选模型。充分考虑配电网规划项目效益耦合和时序关联特性，并将其作为项目优选依据，设计项目优选约束条件。仿真实验测试结果显示与文献方法相比，本文提出的配电网规划项目优选方案成本更低，项目效益较高，有效降低了优选项目建设成本。但是此次研究模型，未曾考虑配电网建设潮流、负荷等因素对项目建设影响，在今后的研究中，还需考虑配电网建设潮流、负荷等影响因素，进一步提高配电网规划项目建设效益。