多AGV和机器集成的多目标柔性作业车间调度研究

马千慧，梁晓磊，刘星雨，张孟镝，黄 凯

武汉科技大学 汽车与交通工程学院，武汉 430065

柔性作业车间调度问题（flexible job-shop scheduling problem，FJSP）包含工序排序和机器选择两个子问题，是典型的NP-hard问题，也一直是国内外学者研究的热点。目前对FJSP的研究主要集中在考虑加工时间且以最小化最大完工时间为目标[1-3]，求解方法也多以智能优化算法为主，如遗传算法[4]、狼群算法[5]、混合遗传杂草算法[6]等。大多数研究中考虑了工件在机器上的加工过程，却忽略了工件的搬运过程。而现代制造业正向智能化方向升级，工件在机器之间的装卸件大多通过自动导引小车（automatic guided vehicle，AGV）进行搬运，AGV在加工设备和运输资源的集成调度及协同优化中发挥的作用成为智能制造系统高效运作的重要支撑，因此考虑AGV调度与FJSP问题的结合有重要的实用价值。

目前对于AGV参与下的FJSP的研究主要集中在机器分配、工序调度、AGV调度分配、AGV路径选择等四个方面，如杨立熙等[7]、张国辉等[8]考虑了工序间的运输时间，但没有考虑运输设备的调度；贺长征等[9]、Zheng等[10]考虑了机器和AGV的集成调度，但都以单目标优化为主，对AGV数量和调度目标两者之间的关系分析不足；在多目标优化问题上，有学者考虑以车间总能量消耗最小和最大完工时间最小为目标[11]、以最小化综合能耗成本和完工时间为目标[12]、以最大完工时间最小和AGV利用率最大为目标[13]构建模型，但较少考虑AGV因素下的优化指标。AGV作为运输设备和约束条件，在加工过程中将其作为调度目标的考虑因素是必要的。在求解算法中，近年研究多采用多目标优化算法进行求解，如鞠录岩等[14]提出改进NSGA算法求解多目标柔性作业车间调度问题，景志强等[15]提出NSGA-Ⅱ和模拟退火算法的混合算法，董海等[16]将入侵肿瘤生长优化算法和NSGA-Ⅲ算法进行混合，但算法对问题的求解效率还需进一步提升。

在实际制造过程中，由于加工任务的到达是随机的，每个工件设置不同的到达时间，有些工件的完工限制在一定时间范围内，需满足客户要求在交货期前完工，因此本文在考虑加工时间的同时，结合考虑工件的到达时间、交货期等多时间因素，集成AGV调度和机器调度，建立多目标柔性作业车间调度模型，研究AGV数量变化与调度目标的关系。在求解方面，针对NSGA-Ⅱ算法运算复杂和精英策略不足的缺点，提出一种改进的NSGA-Ⅱ优化算法对本文模型进行有效求解。

1 机器/AGV双约束的FJSP调度问题描述与建模

1.1 问题描述

假设包含多道工序的n个工件可以在不同的m台机器上进行加工，且有V台相同的AGV在车间运送工件，所有工序按照规定的加工工艺路线在可加工机器集中的机器上加工，一道工序操作完成后，其下一道工序加工前要考虑AGV的运输情况。本文提出在柔性作业车间调度问题中同时调度机器和AGV，充分考虑到达时间、加工时间、运输时间、交货期等多时间因素，建立机器/AGV双约束的FJSP模型，调度以最小化最大完工时间、最小化总延期、最小化设备总负荷为目标。模型假设：零时刻AGV在入库区准备就绪；AGV一次只能运载一个工件，且沿着预定的双向单通道最短路径行驶，且规定某一时刻一条路径上只允许行驶一台AGV；AGV执行完当前运输任务后直接前往下一运输任务加工机器旁，不返回入库区；考虑工件从入库区到各机器和最后一道工序加工完后到出库区的运输时间；任意时刻每台机器只能加工一个工件；不同工件间没有优先级，同一工件各工序存在先后顺序；假定全部工件由AGV运送至出库区即为加工完成；不考虑机器故障、AGV路径冲突和碰撞等因素。

1.2 参数定义

模型参数定义如表1所示。

表1 参数定义Table 1 Parameters definition

其中：

1.3 模型建立

模型约束构建如下：

式（7）表示某时刻某工件只能被一台机器加工；式（8）表示每台AGV每次只接受一个运送任务；式（9）表示AGV需在工件工序加工完成后接受运送任务；式（10）表示AGV零时刻在入库区等待；式（11）表示工件Ji加工完后被送至出库区；式（12）表示同一工件两个相邻工序的加工约束；式（13）表示同一机器上紧前工序的加工约束；式（14）表示工件的第一道工序开始加工前需由AGV从入库区搬运至第一台机器；式（15）表示工件最后一道工序加工完后需由AGV搬运至出库区；式（16）表示AGV完成运送任务Wi,j的结束运输时间为开始运输时间加上运输时间；式（17）表示机器的加工能力限制；式（18）表示AGV的能力限制；式（19）表示交货期限制；式（20）表示当前机器空闲时才能加工工件。

由于考虑了工件的到达时间，且假设AGV运送任务状态分为装卸件两种，则需要探究是否为第一道工序、AGV搬运运送任务到达某一机器时该机器的工作情况：

（1）当AGV执行装件运送任务时，若为第一道工序，AGV工作时间即运输时间；若非第一道工序，AGV工作时间为AGV所在机器、装件点和加工机器三点间的运输时间之和，计算如式（21）所示：

（2）当AGV执行卸件运送任务时，若待接受运送工序已加工完，AGV工作时间为AGV所在机器、待接受运送工序加工完成机器与卸件点三点间的运输时间之和；若未加工完，需判断该工序完工时间与AGV运输时间的大小，AGV工作时间取最大值与该机器到卸件点的运输时间之和。计算公式为：

相应地，考虑AGV运输时间约束和机器可用时间段时，需要探究是否为第一道工序以及机器是否空闲的工作情况：

（1）当机器空闲时，若为第一道工序，工件开始加工时间为到达时间与Tv,Wi,j之和；若非第一道工序，工件开始加工时间为该工序上一道工序的完工时间与Tv,Wi,j之和。计算公式为：

（2）当机器不可用时，若为第一道工序，工件开始加工时间由到达时间与Tv,Wi,j两者之和、机器开始空闲时间中的最大值决定；若非第一道工序，工件开始加工时间由该工序上一道工序的完工时间与Tv,Wi,j之和、机器开始空闲时间中的最大值决定。计算公式为：

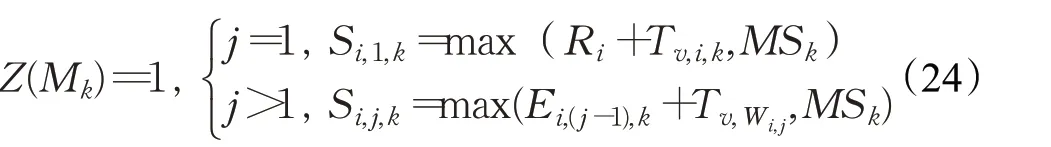
综上，工件的结束加工时间的计算方式为：

根据以上约束模型，考虑到车间效率、客户满意度和设备使用情况，设置最大完工时间、总延期和设备总负荷最小三个目标，目标函数构建如下：

（1）最小化最大完工时间：

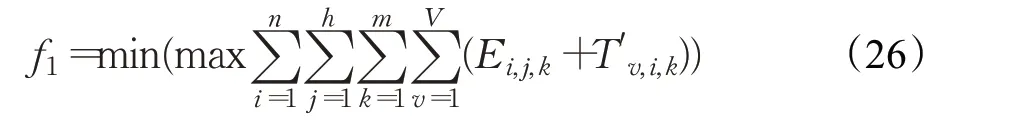
工件从入库到出库整个流程结束表示其加工完成，则工件最大完工时间为结束加工时间与加工完后从最后一台机器到出库区的运输时间之和。

（2）最小化总延期：

为满足交货期限制，减少总延期时间以提高客户满意度。

（3）最小化设备总负荷：

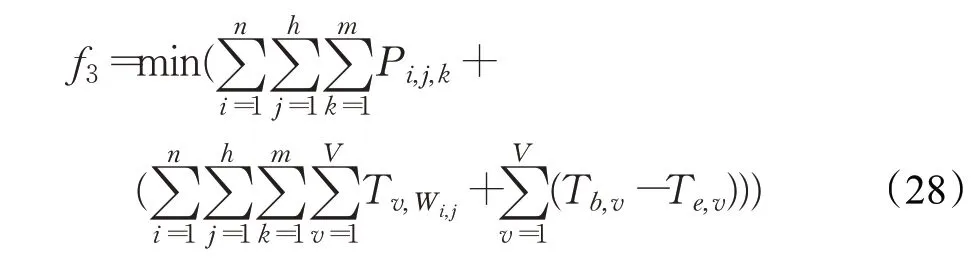
将AGV作为考虑因素加入设备总负荷优化指标中，其中包含机器负荷和AGV负荷（负载和空载），以提高设备利用率。

2 求解算法设计

2.1 AGV调度规则

为了合理分配车间调度资源和提高系统效率，提出新的AGV调度规则以确定加工工件和AGV的分配关系。针对本文FJSP模型特点，AGV调度规则分为单AGV和多AGV两种情况，如图1所示：（1）单AGV时，AGV完成上一运送任务后立即进行下一运送任务运输；（2）多AGV时，如果每台AGV在完成下一工序运输任务的时间节点都大于下一工序能开始加工的时间，则选择最早能完成运输任务的AGV；如果仅有一台AGV在完成下一工序运输任务的时间节点在该工序能开始加工的时间之前，则选择此AGV；如果有多台AGV在完成下一工序运输任务的时间节点在该工序能开始加工的时间之前，则选择其中完成运输任务时AGV运行距离最短的AGV。新的AGV调度规则在工件加工过程中根据不同情况考虑AGV最早到达和距离最短，使得工件在加工时获得一个最早的开始加工时间。

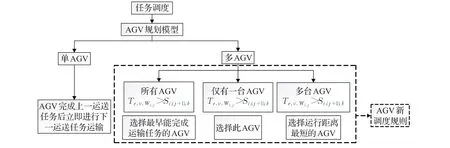
图1 AGV调度规则Fig.1 AGV scheduling rules

2.2 算法编码及解码策略设计

为提高NSGA-Ⅱ算法求解效率，本文设计了基于工序和启发策略的编码和解码策略。以一个3×5（3个工件、5台机器）FJSP问题为例，工件加工及AGV信息如表2所示。

表2 3×5 FJSP问题实例Table 2 Example of 3×5 FJSP problem

针对本文构建模型，采用基于工序的扩展染色体编码，染色体结构如图2所示。该染色体由两部分组成，第一部分采用基于工序的编码，基因位上工件号出现的次数代表该工件的第几道工序，如第一个基因位上的数值2表示工件2的第一道工序，第二个基因位上的数值1表示工件1的第一道工序，以此类推；第二部分采用基于机器的编码，基因位上的数值代表相应工序的可选机器号，如第一个基因位上的数值2代表工件2的第一道工序选择机器2加工，第二个基因位上的数值3代表工件1的第一道工序选择机器3加工，以此类推。

图2 FJSP染色体编码Fig.2 FJSP chromosome coding

上述编码操作可以解决工序顺序和机器分配问题，而AGV的调度体现在解码中。本文构建了一种基于AGV分配的贪婪式解码策略。以图1染色体为例，具体步骤如下：

（1）根据染色体编码可以获得相应基因位的信息，包括工序基因P，加工机器Mk，进行运送任务的AGV号Pv以及AGV接受运送任务时所在的机器M′v,Wi,j，将获取的信息作为解码的输入条件。

（2）从左到右读取染色体基因，转换成相应工序Oi,j和机器Mk，通过选择的加工机器确定加工时间Pi,j,k，得到前置工序Oi,(j－1)的结束加工时间Ei,(j－1),k，前置工序所在机器位置Mv,Wi,j。

（3）确定工序开始加工时间Si,j,k。解码计算时需考虑工件和加工机器的约束，见公式（23）、（24）。

（4）确定AGV运输时间Tv,Wi,j。解码计算时需考虑机器和AGV的双约束，见公式（21）、（22）。

（5）确定AGV号Pv。通过AGV调度规则根据不同情况判断选择最早到达还是距离最短，即判断AGV完成下一工序运输任务的时间节点Te,v,Wi,j与该工序能开始加工的时间节点Si,(j+1),k的大小关系。

（6）确定工序结束加工时间Ei,j,k和完工时间。见公式（23）、（24）、（25）。

（7）重复步骤（2）～（6），直到所有的工件加工完成为止，得到每个工件每道工序的开始加工时间、加工机器、AGV和完工时间，即生成调度方案。

2.3 算法操作算子设计

（1）选择算子

首先对初始种群进行排序并分级，找到种群中所有不被其他个体支配的个体作为第一级非支配个体集合，不断分级操作，直到所有的个体分级完成，再进行拥挤度估计。经过非支配排序和拥挤度计算，本文采用二元锦标赛选择方法，每次随机选择两个个体，优先选择排序等级高的个体，如果排序等级一样，优先选择拥挤度大的个体，如果拥挤度相同则选择序号小的个体。

（2）交叉变异算子

针对染色体编码以及机器可选的特点，在保证可行解的前提下，设计分段交叉和变异操作。

工序交叉：将所有工件随机分成两组J1、J2，随机选择两个不同的父代工序染色体，将F1中属于J1的工序位置保留到Z1，将F2中属于J2的工序位置保留到Z2；将F2中属于J2的工序复制到Z1的剩余位置，将F1中属于J1的工序复制到Z2的剩余位置。其交叉过程见图3（a）所示。

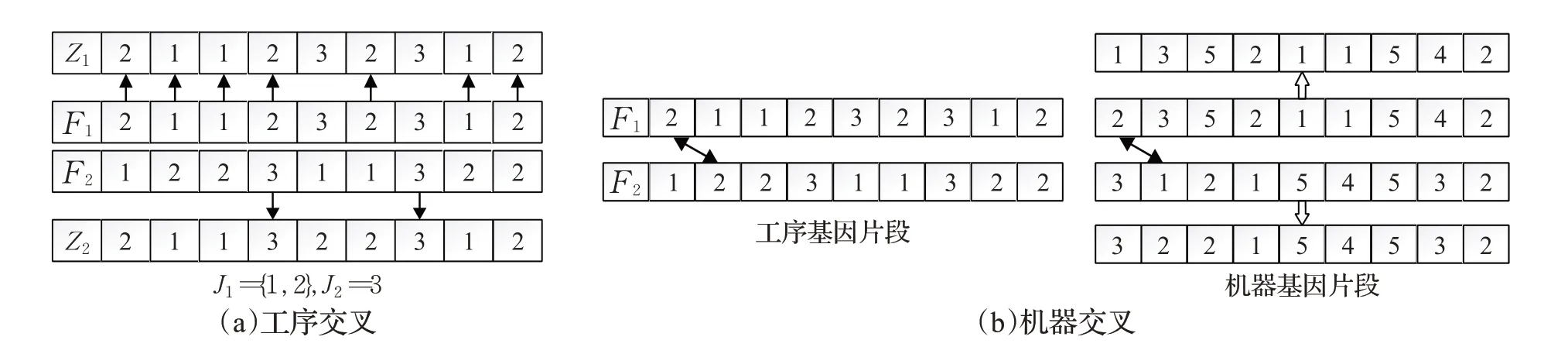
图3 染色体交叉操作过程Fig.3 Chromosome crossover procedure

机器交叉：选择两个不同的父代染色体，随机生成进行机器交叉的工序位置做为父代1交叉的位置，然后与父代2对应的位置进行机器交叉。例如，选择F1中工件2的第一道工序作为交叉位置点，找出F2中此工序的位置，将此位置作为机器基因交叉点。其交叉过程见图3（b）所示。

工序变异：选择一个父代染色体，随机生成两个需要进行工序变异的工序位置，将两个位置的工序进行交换，为满足对应加工工序的机器不变，对机器序列进行重新排序。例如：把工件1的第一道工序与工件3的第二道工序进行交换，交换后此时工件3的第二道工序变为第一道工序，改变了工序顺序，机器选择发生了变化，需对机器进行重新选择，修正之后加工机器可能从机器3变为机器1，机器5变为机器2。其变异过程如图4（a）所示。

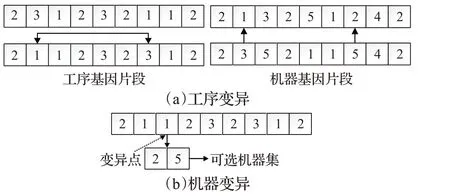
图4 染色体变异操作过程Fig.4 Procedure of chromosome mutation

机器变异：选择一个父代染色体，随机生成多个需要进行机器变异的工序位置，在各工序对应加工的机器集里重新选择机器。例如：选择工件1的第二道工序的位置进行变异，其可选机器集合为{2，5}，生成该集合长度内的随机数r，若r=1，则选择机器2；若r=2，则选择机器5，其变异过程如图4（b）所示。

2.4 改进NSGA-Ⅱ算法

（1）多种群参数控制

多种群中的各种群采用不同的以某类指标为主的搜索方式，给不同的种群赋予不同的控制参数，突破NSGA-Ⅱ仅靠单个群体进行遗传进化的框架。本文目的侧重种群进化完成后使得三个目标相对较优以及处于第一层级非支配序的解分布均匀，具体操作为，对种群进行二元锦标赛选择，对第一个种群选择以非支配排序为主的适合繁殖的父代种群，对第二个种群选择以完工时间最小为主的适合繁殖的父代种群，对第三个种群选择以设备总负荷最小为主的适合繁殖的父代种群，对三个种群分别进行交叉变异操作，引入三个种群同时进行优化搜索，实现多种群的协同进化。

（2）基于Pareto级的去重精英保留策略

首先将第t代产生的新种群Qt放入新的父代种群Pt+1中，然后对上一代父代种群Pt进行非支配排序，产生一系列非支配集Zi并计算拥挤度，将经过非支配排序以后的最优的非支配解存入新的第一层级非支配集Z′1中，再将Z′1中不同的个体放入新的父代种群Pt+1中，即Pt+1=Qt+Z′1。

本文采用的精英保留策略中种群数量不确定，每次迭代只保留第一层级中去掉重复解的个体到下一代中，这样操作保证最优解遗传到下一代，且能避免传统隐形精英保留策略在进化过程中大部分非支配解处于第一层级的非支配曲面造成局部收敛的情况。种群进化过程如图5所示。

图5 种群进化过程Fig.5 Procedure of population evolution

2.5 算法流程

AGV/机器双约束下的改进NSGA-Ⅱ算法求解柔性作业车间调度问题的具体流程如图6所示。

图6 算法流程图Fig.6 Algorithm flowchart

2.6 INSGA-Ⅱ算法时间复杂度分析

假设目标函数个数为M，种群规模为N，从2.5节算法流程可以看出，INSGA-Ⅱ算法寻优主要由六部分组成：第一部分初始化种群，由单次种群搜索行为分析可知，其时间复杂度约为O(MN)；第二部分计算适应度值，其时间复杂度约为O(N1+N2+N3)=O(N′)，Nk为子群k的规模；第三部分快速非支配排序，首先二层循环生成非支配解，该步时间复杂度为O(MN2)，其次访问集合中每一个非支配解得到非支配面，由于每个解最多由N－1个解支配，所以每个解被访问的次数最多为N－1次，该步时间复杂度为O(N2)，综上，快速非支配排序的时间复杂度约为O(MN2)；第四部分拥挤度计算，对每一个体求目标值并找其最大值，其时间复杂度约为O(MNlogN)；第五部分多种群进化，加入三个种群，其时间复杂度约为O(N·3)=O(N)；第六部分精英保留，其时间复杂度约为O(MN)。因此，INSGA-Ⅱ算法的总时间复杂度为：

3 车间调度仿真实例

3.1 案例求解

本文以表3所示的8×8问题实例和表4所示的AGV搬运时间为例，对以最大完工时间、总延期、设备总负荷为优化目标的FJSP问题进行验证。问题规模设置为工件数n=8，机器数m=8，AGV数V=3。采用Matlab 2018b进行编程实现，实验在平台（Intel®Core™i5-6500 CPU@3.20 GHz 3.19 GHz，内存8.00 GB）上进行。算法参数设置为：种群规模P=200，最大迭代次数M=100，交叉概率Pc=0.8，变异概率Pm=0.1。

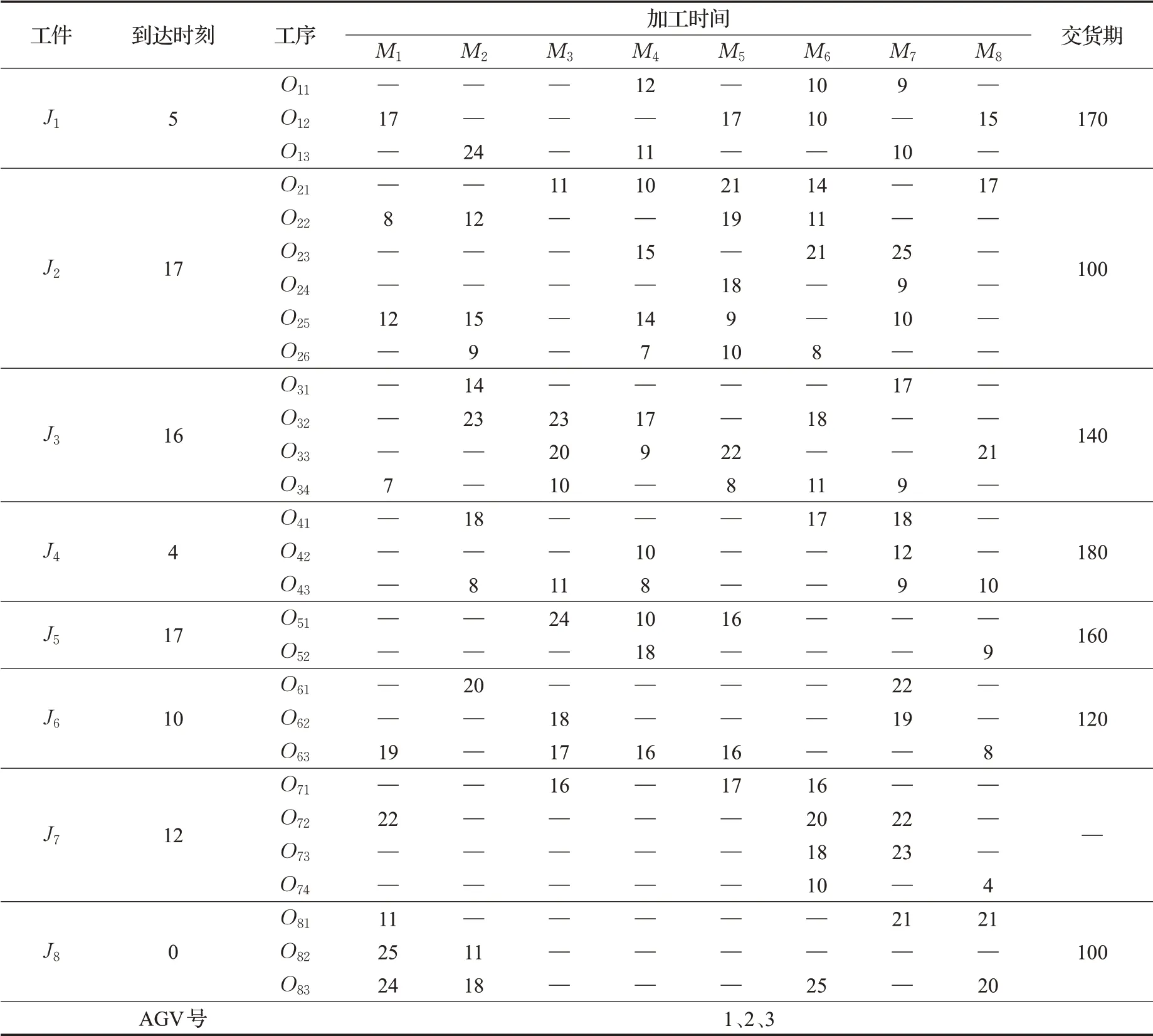
表3 具有工件到达时间和交货期的8×8 FJSP问题实例Table 3 Example of 8×8 FJSP problem with workpiece arrival time and delivery date单位：min

表4 AGV搬运时间Table 4 AGV handling time 单位：min

实验结果如图7（a）所示，其中机器加工时间段用工件号、工序号、加工时间构成的字符串进行标记，即p（工件，工序）=加工时间；AGV运输时间段分为空载和负载两个阶段，分别用虚线框和实线框标记，图中数字代表各个位置节点。方案中调度的3个目标最佳值分别为最大完工时间121、总延期13、设备总负荷568。从图7（a）中可以看出，AGV存在无效运输时间段，如空载段10-6-6。分析可知此时待运送工件的下一道工序仍在同一机器上加工，不需搬运。因此，增加如下约束：相同工件的不同操作工序在同一台机器上加工不需要AGV运输。校正后调度解甘特图如图7（b）所示，此时3个目标最佳值分别为最大完工时间112、总延期12、设备总负荷561，获得了更优秀的解。

图7 8×8案例调度甘特图Fig.7 8×8 case scheduling Gantt chart

校正后该方案得到AGV的运输时间矩阵为：

其中，每个矩阵第一列数值表示AGV号，第二列表示AGV位置节点，第三列表示工件位置节点，第四列表示工件加工机器位置节点，第五列表示AGV空载开始时间，第六列表示AGV负载开始时间，第七列表示AGV负载结束时间。含义如下：第八个工件的第一道工序O81开始加工时间为其到达时间0、小车1从入库区搬运O81到机器1的运输时间4之和即4，对应AGV时间矩阵为[1 9 9 1 0 0 4]；小车1负载结束时间为4，由位置1行驶至入库区搬运工序O21到机器3上加工，其开始加工时间计算判断小车到达时间和工件到达时间的大小取最大值，即max（4+4，17）+6=23，对应AGV时间矩阵[1 1 9 3 13 17 23]，以此类推，最终确定调度方案。

针对最大完工时间、总延期以及设备总负荷的3个目标的柔性作业车间调度问题，用本文改进NSGA-Ⅱ算法求解得到的Pareto前沿如图8所示，各解相互之间重叠小，解集覆盖性较好。

3.2 AGV数量与调度目标关系分析

为研究AGV数量变化对调度目标的影响，本文基于8×8算例，取不同数量的AGV，进行独立测试，分别计算20次取平均值，得到结果如图9所示。从图9中可以看出，当AGV数量超过3时，最大完工时间和总延期变化趋于平缓，而由于AGV增加造成AGV空载减少，设备总负荷会相应减少。总的来说，随着AGV数量的增加，三个目标函数值会逐渐减小，且减小的幅度会越来越小，即对提高相同任务调度效率的影响随AGV数量的增加而减小。实际生产过程中，在考虑AGV成本的情况下，选择相同调度效率下AGV数量少的方案。

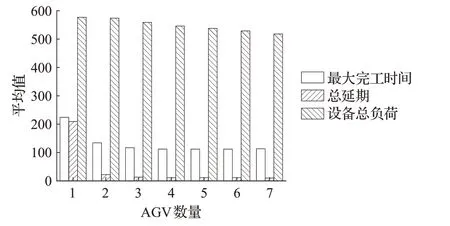
图9 AGV数量对目标函数值的影响Fig.9 Influence of AGV numbers on objective functions values

3.3 算法性能测试

为测试算法求解能力，设置不同AGV数量，在相同规模问题（8×8算例）下，实验中AGV数V＜n，种群规模P=200，最大迭代次数M=100，交叉概率Pc=0.8，变异概率Pm=0.1。

不同AGV规模案例中，INSGA-Ⅱ算法求解8×8算例的3个目标函数平均收敛曲线分别如图10所示。由图10可以看出，随着AGV数量的增加，算法收敛速度先加快，后不变，3个目标迭代到一定程度时均收敛到最优值，可以证明改进的NSGA-Ⅱ算法在求解此类调度问题上具有较强的搜索能力。

图10 不同AGV数量下目标函数平均收敛曲线图Fig.10 Average convergence curves of objective functions under different AGV quantities

此外，构建AGV=7案例，选择多目标粒子群优化（multi-objective particle swarm optimization，MOPSO）算法[17]、混合差分进化（hybrid differential evolution，HDE）算法[18]、非支配排序遗传（non-dominated sorting genetic algorithm-Ⅱ，NSGA-Ⅱ）算法与本文算法进行性能对比。AGV=7时以上3种算法下的目标函数平均收敛曲线如图11所示。结果可以看出，INSGA-Ⅱ算法克服了MOPSO和HDE求解AGV机器调度问题的过早收敛现象，且较NSGA-Ⅱ有更好的优化效果。体现了本文改进算法的可扩展性。

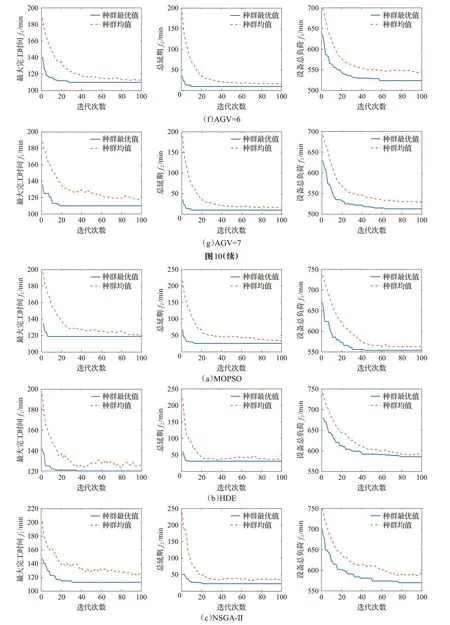
图11 AGV=7时对比算法下的目标函数平均收敛曲线图Fig.11 Average convergence curves of objective functions under comparative algorithm at AGV=7

为进一步验证模型和INSGA-Ⅱ算法及优化策略的有效性，分别使用文献中3×5算例[19]、10×8算例[20]、12×10算例[21]和本文8×8算例数据进行模型和算法测试。文献算例中未指明的AGV运输时间采用表4中数据。4种多目标优化算法在每组测试数据下分别运行20次取平均值，得到对比结果如表5所示。结果显示，改进算法均获得更高质量的解，证明本文INSGA-Ⅱ算法能够有效求解带有AGV约束的多目标柔性作业车间调度问题，且对大规模问题也更好地优化效果。

表5 不同案例算法对比结果Table 5 Comparison results of different case algorithms单位：min

4 结论

针对FJSP中较少考虑运输过程的不足，本文在加工过程的基础上增加了运输资源AGV的调度，考虑多时间因素和一个或多个AGV组成的柔性作业车间系统，用于解决机器和多个相同AGV的同时调度问题。针对任务分配和AGV调度对模型进行多目标优化，设计了改进NSGA-Ⅱ算法，提出了基于AGV分配的贪婪式解码策略，同时结合多种群和精英保留策略提高算法的搜索能力。通过与其他算法对比实验，结果证明了本文提出模型的有效性，且改进算法能够获得优秀的调度结果。在下一步研究工作中，将重点研究模型中随机因素对FJSP问题的影响以及进一步改善算法求解效率。