东海区域基于有限元软件的筒型基础校核分析
严维峰,许文兵,李 根,李利飞,丁意达,施览玲
1.中海石油有限公司上海分公司,上海 200050
2.中国石油大学(北京),北京 102200
筒型基础具有施工便利、造价低、投资少、高机动性和灵活性、可持续使用等特点,近二十多年来在海洋工程上得到广泛的应用,并且有着广阔的发展前景。利用潜水泵,可以很容易地将筒型基础沉放到海底土内,因此常用于各种海上结构设施,如浮筒定位、海上军事工程、导管架、灯塔、船只系泊和海上石油钻取等各种平台。建造周期短、投入低且安装工艺简单的筒型基础桩基结构能够为油气资源丰富但丰度较低区块的开发以及对开发作业敏感的海域探井的布置和开发提供有力支持,大幅度降低勘探开发成本,对增储上产具有极为重要的意义。
李文帅等[1]针对沉贯过程中土体变形大的特点,运用颗粒流软件建立了筒型基础动态沉贯安装模型;刘润等[2]开展了比较完整的室内模型试验研究,模拟了筒型基础的自重沉放与负压沉贯过程,基于相关理论推导了筒型基础沉放最大径向影响范围计算公式;Xing等[3]基于上部荷载特性和土体参数,探究黏性土中筒型基础承载力规律,总结极限水平荷载和极限弯矩荷载对筒型基础破坏的影响;马文冠等[4]开展了粉土中筒型基础的现场贯入试验,观测了自重下沉阶段与负压贯入阶段筒型基础贯入阻力与贯入深度的关系,提出了粉土中计算沉贯阻力的方法,并对不同筒端形式的减阻效果进行了深入分析;Xu等[5]通过建立单桩复合管式基础-基础的大型三维仿真模型,计算其在各种荷载共同作用下的应力和变形,评价了单桩复合管式基础的稳定性。通过对前人的研究进行总结,目前尚缺少结合具体现场的有限元分析,使用SACS和PLAXIS进行吸力筒导管架基础结构一体化设计,可以有效模拟验证其施工可行性,以期为现场施工提供指导。
本研究针对东海某海域环境条件和土质情况,利用迭代法比选出同时满足稳定性和经济性要求的筒型基础。
1 理论模型
1.1 压拔承载力计算模型
现阶段,压拔承载力Qs(kN)的计算参考API RP 2A-WSD(2005)[6]中6.4节的要求:

式中:f为导管单位面积表面摩擦力,kPa;As为桩侧表面积,m²;α为无量纲系数;Su为目标区域土样的不排水抗剪强度,kPa;Ψ为讨论点的系数,无量纲;P′0为计算点的有效上覆土压力,kPa;K为水平侧压力系数(若未完全闭塞,K取0.8;若完全闭塞,则K取1.0);P0为有效上覆应力,kPa;δ为桩土界面摩擦角,(°);γi为土层的有效重度,kN/m3;hi为各土层厚度,m。
同时,需要满足以下公式:

式中:Qt为抗拔承载力,kN;Qs外侧为筒外壁侧摩阻力,kN;Qs内侧为筒内壁侧摩阻力,kN;G桶内土重为桶内土体重量,kN;G桶重为筒型基础自重,kN;T为抗拔力设计值,kN;Qk为抗压承载力,kN;Qs为侧壁摩擦力,kN/m²;Qb为桶顶盖轴向承载力,kN;q为单位桩端承载力,kPa;Ap为筒顶盖面积,m²;S为承载力设计值,kN。
1.2 沉贯阻力计算模型
桶基础结构下沉入土时的下沉阻力主要包括桶壁的侧摩阻力和桶端部的端阻力两部分,桶形基础下沉阻力参照《Offshore soil mechanics and geotechnical engineering》 (DNV GL-RP-C212) 第7.3.3节筒的沉贯阻力计算公式进行计算:
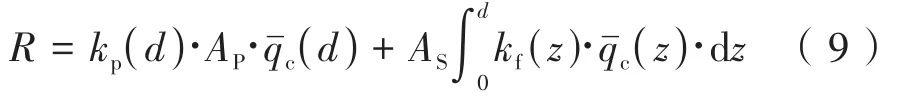
式中:R为沉贯阻力,kN;kp(d)为筒端端阻力的经验系数;d为复合筒贯入深度,m;Ap为裙底面积,m2;c(d) 为筒端持力层锥尖阻力,kPa;c(z)为土层不排水剪切强度,kPa;AS为筒裙面积(内外),m2/m;kf(z)为侧摩阻力经验系数。
2 有限元分析
2.1 建立模型
筒型基础计算模型(见图1)由筒型基础结构、土壤和结构-土界面单元组成。土壤本构模型采用HS土体硬化模型,筒型基础采用3D板单元,筒体和土壤之间设置界面单元。

图1 筒型基础计算模型
考虑到目标区块的土质分层情况及上部载荷估算值,设计筒型基础直径13 m,筒高25 m,壁厚58 mm,筒顶盖板板厚55 mm。筒顶加强肋板板厚40 mm,共8块,均匀布置于筒顶盖板之上。
压载工况:水平力Fx=6 062 kN,竖向压力Fz=50 160 kN,弯矩My=5 785 kN·m。
上拔工况:水平力Fx=5 989 kN,竖向拉力Fz=43 018 kN,弯矩My=4 644 kN·m。
2.2 筒顶压拔承载力分析
筒型基础的设计入土深度25 m。根据式(1)~式(8),计算得到如表1~表4所示的载荷分析结果。

表1 土层基本参数

表2 载荷分析统计

表3 抗拔承载力校核结果

表4 抗压承载力校核结果
根据以上分析得到:给出的筒型基础尺寸下,其抗压承载力和抗拔承载力安全系数均满足API中规定的要求(>1.5)。
2.3 在位稳定性分析
提取SACS模型中的合水平力与合弯矩,且二者同向。压载、上拔工况下的位移云图见图2、图3。

图2 压载工况下的位移云图

图3 上拔工况下的位移云图
压载工况下:最大水平位移100.6 mm,小于1%D(即130 mm);最大不均匀沉降193.62 mm;筒顶转角9.2‰。
上拔工况下:最大水平位移65.8 mm,小于1%D(即130 mm);最大向上位移84.3 mm;筒顶转角5.65‰。
2.4 沉贯阻力计算和屈曲验算
根据式(9)并根据不同入泥深度对应的沉贯阻力(见图4),可以得到最大沉贯阻力。

图4 筒型基础沉桩阻力随入泥深度变化规律
根据以上结果可以得到,沉贯到位所需要的压差值可能为510.16 kPa,在浅层夹砂层的下沉难度较大。建议在现场作业过程中采用550 kPa以上的设备进行安装作业。
在使用最大沉贯阻力设计的条件下,沉贯过程中屈曲应力小于屈曲强度,结构满足要求。圆筒壳体屈曲局部稳定参照《Buckling strength of shells》(DNV GL-RP-C202)进行计算。
对于经受一项或多项荷载(轴拉荷载、轴压荷载、弯曲荷载、环向压或拉荷载、扭转、剪切)的壳结构,其稳定性需满足如下要求:

设计屈曲强度fksd按如下公式计算:

式中:σj,Sd为设计等效mise应力,N/m2;fksd为壳体的设计屈曲强度,N/m2;fks为壳体的特征屈曲强度,N/m2;γM为材料系数,无量纲。材料系数γM按照如下公式取值:

σj,Sd按如下公式计算:

式中:σa,Sd为轴向荷载对应的设计轴向应力(拉为正),N/m2;σm,Sd为弯矩荷载对应的设计弯曲应力(拉为正),N/m2;σh,Sd为外部水压荷载对应的设计环向应力(拉为正),N/m2;τSd为扭转荷载和剪切荷载对应的设计剪切应力,N/m2。
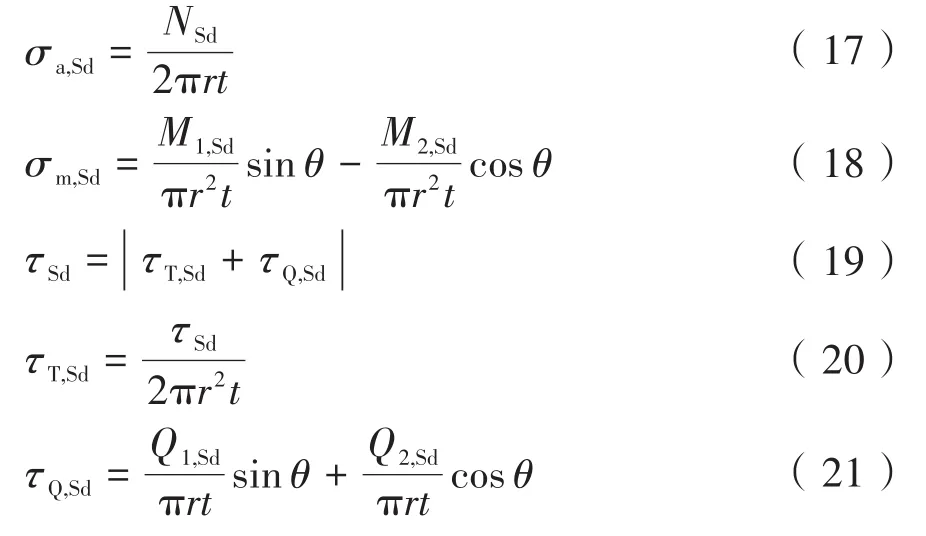

式中:NSd为轴向荷载,N;M1,Sd,M2,Sd为弯矩荷载,N;Q1,Sd,Q2,Sd为剪切荷载,N;τSd为扭转荷载,N;PSd为环向荷载,N。
屈曲强度特征值fks按下列公式计算:

式中:fEa为轴向荷载对应的弹性屈曲强度,N/m2;fEm为弯矩荷载对应的弹性屈曲强度,N/m2;fEh为水压力、外部压力和圆周压力对应的弹性屈曲强度,N/m2;fEτ为扭转、剪切对应的弹性屈曲强度,N/m2。
结合校核分析方法及数值模拟结果,得到筒型基础在沉桩过程中屈曲应力和屈曲强度随入泥深度的变化规律,如图5所示。
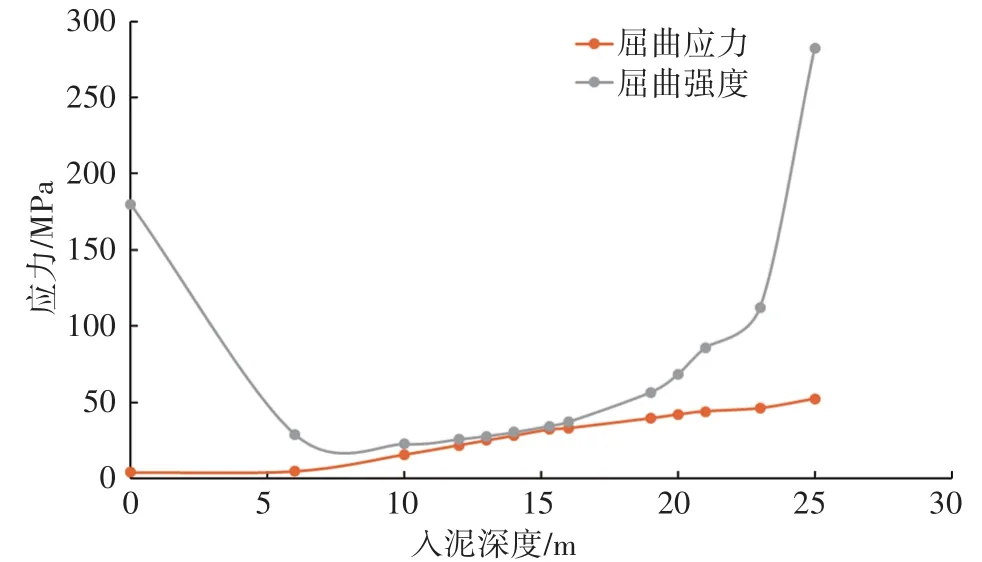
图5 筒型基础沉桩过程中屈曲应力和屈曲强度随深度变化规律
从图5可以看出:随着入泥深度的增加屈曲应力逐渐增大,而屈曲强度则先减小后增大,表明筒型基础沉入至硬土层(砂粘互层或砂层)时屈曲强度降低;0~25 m的入泥深度范围之内,屈曲强度均大于屈曲应力,即满足规范对屈曲应力的要求;入泥深度为7.5~16 m时,屈曲强度接近屈曲应力,实际作业过程中需要放慢沉入速度并随时观察筒型基础的变形情况,防止发生屈曲变形。
3 结论
(1)开展了压载工况和上拔工况下的承载力分析,结果表明所给筒型基础参数满足相关规范中对抗拔阻力和承载力的要求。筒型基础得到其最大水平位移小于1%D,满足稳性要求;得到了最大不均匀沉降和筒顶转角,可为现场安装施工提供参考数据。
(2)开展了筒型基础沉桩阻力计算和屈曲分析,得知随着入泥深度的增加屈曲应力逐渐增大,而屈曲强度则先减小后增大,表明筒型基础沉入至硬土层(砂粘互层或砂层)时屈曲强度降低;0~25 m的入泥深度范围之内,屈曲强度均大于屈曲应力,即满足规范对屈曲应力的要求;入泥深度为7.5~16 m时,屈曲强度接近屈曲应力,实际作业过程中需要放慢沉入速度并随时观察筒型基础的变形情况,防止发生屈曲变形。

