基于特性方程和模拟分析的输气管道沿程压力变化研究
马 莹,刘佳庆,孙 晔,郭大凯,王广辉,梁昌晶
1.中国石油华北油田公司第一采油厂,河北任丘 062552
2.中国石油华北油田公司,河北任丘 062552
根据我国碳达峰、碳中和的目标,天然气在能源转型中的作用不断凸显,我国兴建了一批互联互通、贯通南北、覆盖全国的输气管道,但管道完整性一直是关注的重点[1]。由于管网建设时间、管材规格、设计压力和沿程地区等级的不同,埋地管道的泄漏检测定位难度较大。从检测参数角度而言常用技术手段有直接法和间接法,但这些方法受天然气性质和环境的影响,定位准确度较低,且对于运行人员的可操作性较差[2-4]。
随着智慧管网和数字孪生体的应用,管道沿程温度、压力和流量等数据可从SCADA系统中轻松获取,如能从其中挖掘管道泄漏信息并进行定位,将极大节省人力、物力和财力。张红兵等[5]基于流体力学和热力学建立了气体流动方程,并采用显式特征差分法对数据进行迭代计算,但模型只适用于干气管道;张静等[6]将定位问题转化为寻优问题,通过智能算法对龙格库塔进行改进,极大节省了运算时间,但模型的重复性有待论证;靳新迪等[7]对环状管网进行多工况泄漏检测,参照指纹相似特征将泄漏图形进行分类处理,但文中管道长度较短,运行压力也较低,与实际工况有一定差距。以上研究也未对泄漏引起的沿程压力变化进行分析,同时未涉及多点泄漏造成的参数影响。基于上述局限性,从管道特征方程出发,分析单点泄漏和多点泄漏下管道沿程压力分布情况,并利用TGNET软件建立输气管道模型[8-9],验证理论分析结果,根据压差幅值与泄漏时间、泄漏位置、泄漏点个数的关系进行定位。研究结果可为基于管道瞬态模型的泄漏检测提供实际参考。
1 特性方程
1.1 单点泄漏管道沿程压力分布情况
单点泄漏模型示意见图1。
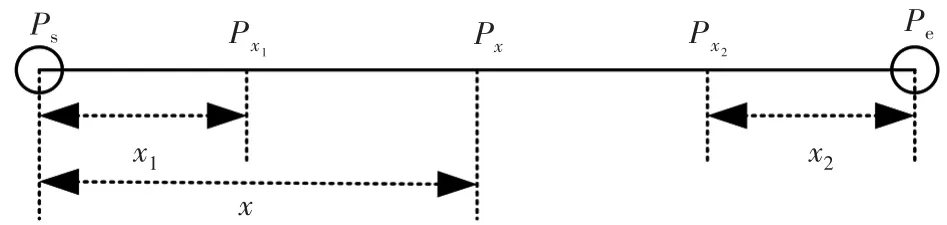
图1 单点泄漏模型示意
根据管道压降与流量的关系[10-11],泄漏点x之前的管道特性方程如下:

式中:Ps、Ps′分别为泄漏前、后的起点压力,kPa;分别为泄漏前、后距离起点x1位置处的压力,kPa;C为管道特性参数;Q为泄漏前介质体积流量,m3/h;Q′为x处泄漏导致的上游流量,m3/h。
将式 (1) -式 (2),令 ΔPs=Ps-Ps′,,得:

泄漏后,泄漏点之前的流量会增大,大于原来的正常流量,泄漏点之后的流量会减小,且泄漏点流量越大,这种趋势越明显,有Q′>Q。此时公式(3)中等号左边视为定值,故泄漏后沿程压力均下降,x1越大,泄漏前后的压差ΔPx1越大。泄漏点x之后的管道特性方程如下:

式中:Pe、Pe′分别为泄漏前、后的末点压力,kPa;分别为为泄漏前、后距离末点x2位置处的压力,kPa;Q"为x处泄漏导致的下游流量,m3/h。
将式 (3) -式 (4),令 ΔPe=Pe-Pe′,,得:

根据Q>Q",泄漏后沿程压力均下降,x2越大,泄漏前后的压差ΔPx2越大。
1.2 多点泄漏管道沿程压力分布情况
多点泄漏模型示意见图2。

图2 多点泄漏模型示意
多点泄漏沿程压力分布情况与单点泄漏类似,此时可将不同泄漏点之间的距离最小化,视为同一个泄漏点,故不再分析泄漏点前和泄漏点后的压力分布情况,只分析两个泄漏点之间的压力分布情况,特性方程如下:
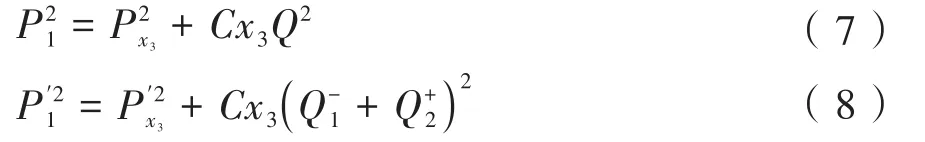
式中:P1、P1′分别为泄漏前、后泄漏点1的压力,kPa;Px3、Px3′分别为泄漏前、后距离泄漏点1下游x3处的压力,kPa;Q1-为泄漏点1的下游流量,m3/h;Q2+为泄漏点2的上游流量,m3/h。
将式 (7) -式 (8),令 ΔP1=P1-P1′,,得:
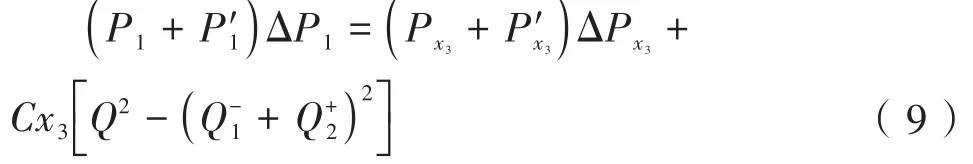
泄漏后,Q>Q1-+Q2+,且P1>P1′,ΔPx3>ΔPx3′,有ΔP1<ΔPx3,则x3处的压差介于泄漏点1和泄漏点2之间,且x3越大,x3处泄漏前后的压差ΔPx3越大。
1.3 泄漏点处压力情况
对图2多点泄漏进行分析,当两点同时泄漏时,泄漏点1和泄漏点2距离起点分别为x4、x5,此时泄漏点2的特性方程如下:
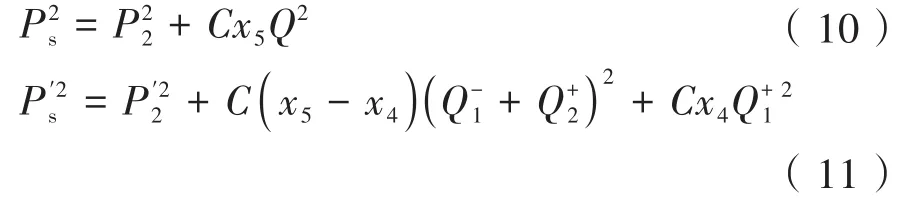
将式(10)-式(11),得:

泄漏后,Q1+>Q>Q1-,Q2+>Q>Q2-,此时x4、x5之间的距离无法弥补泄漏点1上游的流量增加,则ΔPs<ΔP2,同理根据泄漏点1的特性方程可以得到ΔPs<ΔP1,即泄漏点处的压差幅值大于管道其余位置,距离泄漏点越近,泄漏前后的压差幅值越大。
当x4-x5=0时,两个泄漏点变为1个泄漏点,结果与多点泄漏一致,泄漏点距离起点或末点越远,泄漏前、后的压差幅值越大。另外,泄漏孔径的增加会使泄漏点的上游流量不断增加、下游流量不断减少,则泄漏处的压差也不断增大。
2 模拟分析
2.1 模型建立
利用Pipeline Studio中的TGNET模块建立输气管道模型,包括气源、负荷和管道。管道总长为100 km,均分为10段(A~J),管径719 mm,壁厚9 mm,绝对当量粗糙度0.025 mm;不考虑管道高程变化,关闭传热和组分跟踪模型,在每段管道之间设置节点1~9进行监测,管网拓扑结构见图3。
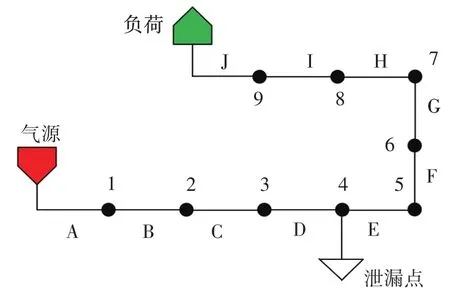
图3 模拟管网拓扑结构
2.2 参数设定
气源组分见表1,气体状态方程选用BWRS,摩阻计算选用Colerook公式,初始条件为“控制-约束”逻辑,起点最大流量300 km3/h,末点最小压力4 MPa,初始泄漏孔径10 mm。

表1 气源组分摩尔分数 单位:%
模拟过程为动态,总时长300 s,前60 s为正常工况,61~300 s为泄漏工况,迭代步长为5 s。
2.3 结果与讨论
2.3.1 单点泄漏压差分布
以泄漏点位于节点5、泄漏孔径10 mm为例,模拟不同节点压差随时间变化的趋势,见图4。在前60 s未泄漏时,节点压差均为0;泄漏后,各节点压差先迅速增加后缓慢增加,最后趋于稳定状态。不同节点压差的上升幅度有所不同,节点5在泄漏90 s后,压差达到稳定;而节点1在泄漏70 s后,压差达到稳定。可见距离泄漏点越近,受到的流量扰动越大,管内压力达到平衡状态所需的时间越长。

图4 不同节点压差随时间变化的趋势(单点泄漏)
模拟不同时间下的沿程压差分布情况,见图5,节点5的压差幅值最大,其次为节点6和节点4,节点1和节点8最小,可见在泄漏点处压差幅值达到峰值。此外,相同泄漏时间下,下游节点压差大于上游节点,这是由于气源采用最大流量模式,泄漏时流量对下游的影响远大于上游。

图5 不同时间下的沿程压差分布(单点泄漏)
2.3.2 多点泄漏压差分布
以泄漏点分别位于节点4和节点5、泄漏孔径10 mm为例,模拟不同节点压差随时间变化的趋势,见图6。此时节点4、5的压差幅值最大,远大于单点泄漏时节点5的压差,节点3、7距离最近泄漏点的距离不一样,但由于泄漏对下游的影响较大,导致节点7的压差在稳定阶段上升至与节点3一致。
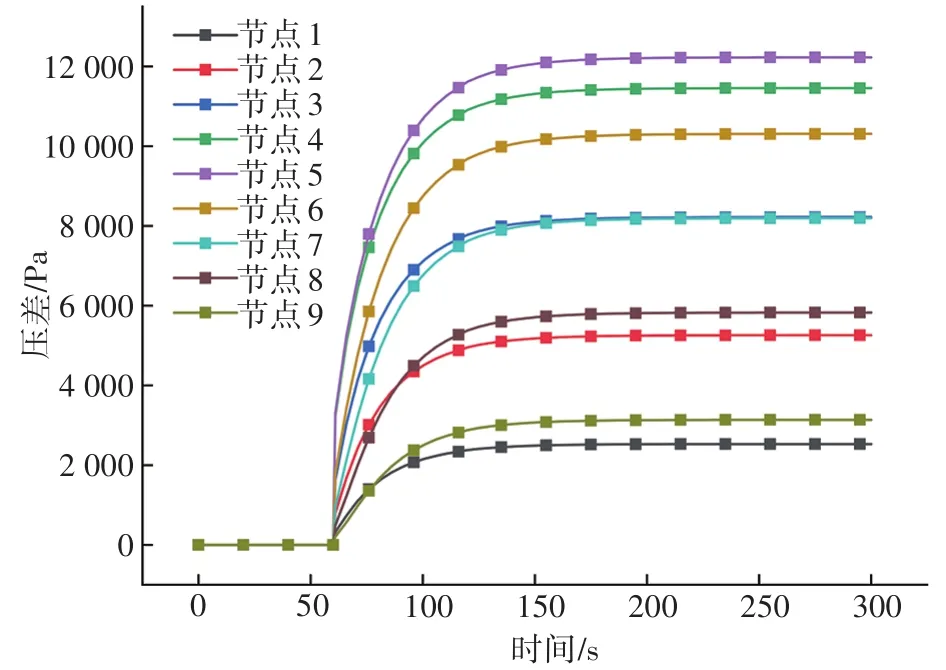
图6 不同节点压差随时间变化的趋势(多点泄漏)
模拟不同时间下的沿程压差分布情况,见图7。多点泄漏压差变化与单点泄漏类似,只是随着时间延长,两个泄漏点的压差幅值相差越来越明显,管道中点附近的泄漏压差最大。

图7 不同时间下的沿程压差分布(多点泄漏)
2.3.3 泄漏点位置对压差分布影响
模拟单点泄漏不同泄漏位置下压差随时间的变化趋势,见图8。
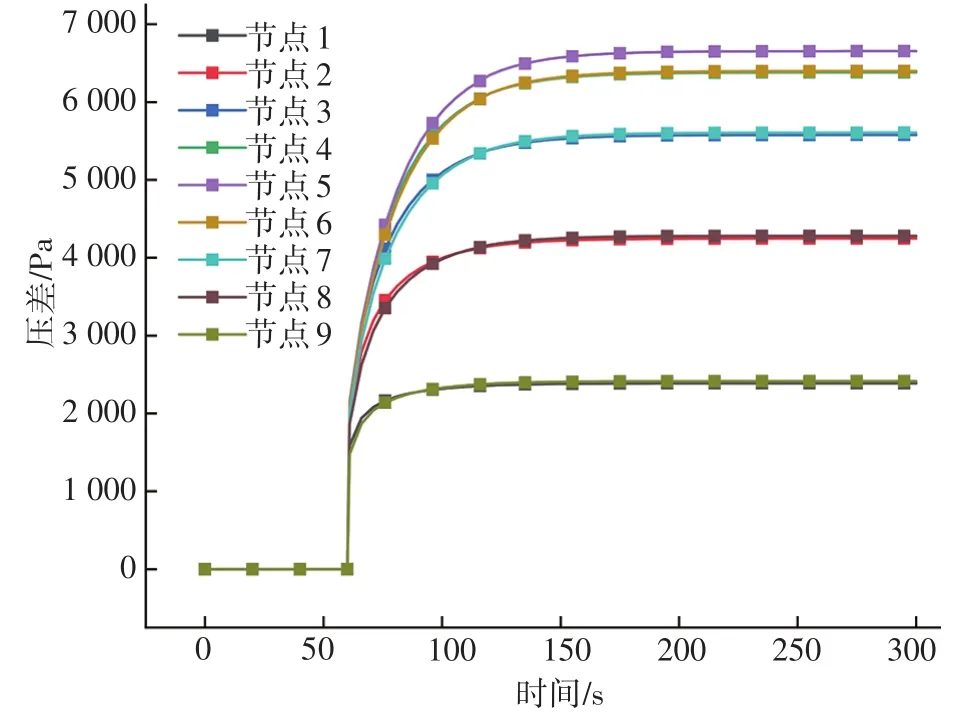
图8 不同泄漏位置压差随时间的变化趋势(单点泄漏)
节点5泄漏前、后的压差最大,围绕节点5呈对称分布的上、下游节点压差分布基本一致,泄漏点距离起点或末点越近,泄漏前、后的压差幅值越小。
模拟稳态300 s时单点泄漏情况下不同泄漏位置对应的沿程压差分布情况,见图9。压差最大位置与泄漏点位置一一对应,且对于同一监测点,当监测点位于泄漏点之前时,泄漏点距离起点越近,压差幅值越大;当监测点位于泄漏点之后时,泄漏点距离起点越近,压差幅值越小。
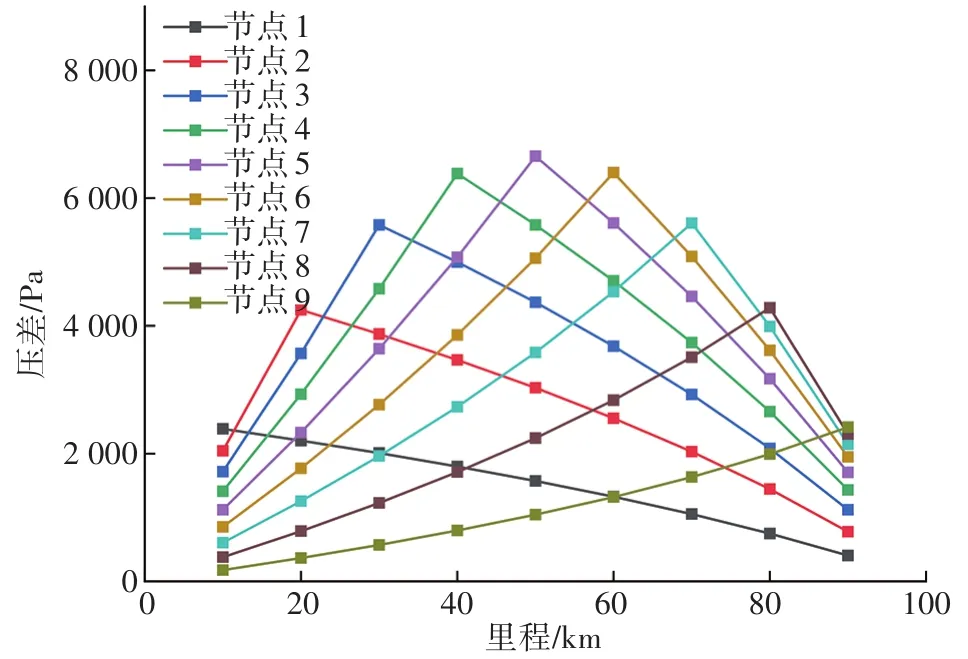
图9 不同泄漏位置对应的沿程压差分布(单点泄漏)
模拟多点泄漏情况下,不同泄漏位置对应的沿程压差分布,见图10。当泄漏点间距保持不变时,靠近起点,压差曲线向左下方移动;当泄漏点间距加大时,压差曲线整体向下方偏移,但泄漏点前后的压差变化不大。

图10 不同泄漏位置下的沿程压差分布(多点泄漏)
2.3.4 泄漏点个数对压差分布的影响
模拟稳态300 s时不同泄漏点个数下的沿程压差分布情况,见图11。多点泄漏的压差幅值远大于单点泄漏,且多点泄漏的压差幅值不是单点泄漏幅值的简单叠加,而是略小于叠加幅值。此外,泄漏点越多,各监测点的压差幅值越大,多点泄漏与叠加幅值的差距也越大。

图11 不同泄漏点个数下的沿程压差分布
3 实例验证
根据上述研究,无论是单点泄漏还是多点泄漏,其泄漏处均在压差最大的位置,通过TGNET建立管道模型模拟正常状态下的沿程压力分布,将其与SCADA系统采集的沿程压力分布进行对比,实时监测压差分布情况,进行定位和监测,对于单点泄漏的定位公式如下:

多点泄漏的定位需根据式(12)计算,但x4、x5均未知,因此只能根据单点定位公式进行粗定位。根据输气管道设计规范中不同地区等级的划分,三级地区阀室间距不超过16 km,四级地区的阀室间距不超过8 km,压力变送器应设置在阀室、分气点的上下游,故多点泄漏的间距不会太大,以粗定位结果为基础,再采用ACVG、DCVG对防腐层破损点进行检测,或通过红外成像技术进行细定位,可有效减少盲目搜索的范围。
以华北油田永清东线SCADA系统进行实时验证,该输气线起点永清站、终点北京东郊门站,管径219 mm×6 mm,全长68 km,管材为20碳钢,1985年投产,设计压力4 MPa。因运行时间较长,时常出现漏点,不仅造成经济损失,也给北京供气安全造成压力。泄漏工况与分气工况类似,利用分压站处模拟单点泄漏,利用分压站和10号阀室内放空管道模拟多点泄漏,泄漏定位参数见表2。

表2 泄漏定位参数
单点泄漏定位结果为34.18 km,定位误差为3.57%;多点泄漏定位结果为36.01 km,在两个泄漏点之间且靠近分压站,可能与分压站分压流量较大有关,与分压站相比定位误差为9.12%,与10号阀室相比定位误差为19.97%。虽然多点泄漏的定位误差较大,但定位结果可优先确定大的泄漏孔径,对于确定维抢修的地点具有实际意义。
4 结论
(1)对泄漏前后的管道特性方程进行分析,并采用TGNET软件建立管网模型进行验证,结果表明:单点泄漏与多点泄漏的压差规律类似,泄漏开始后,节点压差先迅速增加后缓慢增加并趋于稳定,距离泄漏点越近,管内压力达到平衡状态所需的时间越长。
(2)泄漏处的压差最大,泄漏位置对压差影响较大,泄漏点距离起点或末点越近,泄漏前后的压差越小;多点泄漏的压差远大于单点泄漏,且多点泄漏不是单点泄漏压差幅值的叠加。
(3)现场SCADA系统并不是在管道沿线所有点布置,故根据两个压力偏差较大的点可以估算管道泄漏位置,验证后单点泄漏的定位误差为3.57%,多点泄漏的定位误差为9.12%。

