二次函数的应用问题

文／李瑶

二次函数是反映现实世界中变量间的数量关系和变化规律的常见的数学模型，是初中阶段学习的重难点之一。同时，二次函数在实际生活中的应用也十分广泛。下面就以2022年中考题中的利润和面积问题为例进行分析解读。

问题1利润问题

例1（2022·山东滨州）某种商品每件的进价为10元，若每件按20元的价格销售，则每月能卖出360件；若每件按30元的价格销售，则每月能卖出60件。假定每月的销售件数y是销售价格x（单位：元/件）的一次函数。

（1）求y关于x的函数表达式；

（2）当销售价格定为多少元/件时，每月获得的利润最大？并求此最大利润。

【分析】（1）设一次函数的一般形式，利用待定系数法，解出k和b，即可得到y关于x的函数表达式。

（2）根据等量关系“利润=销量×（售价-进价）”，结合（1）中的函数表达式，列出二次函数表达式，配方后依据二次函数的性质即可求得利润最大值。

解：（1）设y=kx+b（k≠0），

将（20，360）、（30，60）分别代入，

所以y=-30x+960。

（2）设每月获得的利润为w元，则

∵-30＜0，

∴当x=21时，w最大，最大值为3630。

答：当销售价格定为21元/件时，每月获得的利润最大，最大利润为3630元。

【点评】本题考查的是一次函数与二次函数在销售方面的综合应用。解题的关键是找准等量关系并明确二次函数的表达式，然后利用二次函数的性质求最值。

问题2面积问题

例2（2022·江苏无锡）某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一面靠墙（墙的长度为10m），另外三面用栅栏围成，中间再用栅栏把它分成两个面积为1∶2的矩形，已知栅栏的总长度为24m，设较小矩形的宽为xm（如图1）。

图1

（1）若矩形养殖场的总面积为36m2，求此时x的值；

（2）当x为多少时，矩形养殖场的总面积最大？最大值为多少？

【分析】（1）首先，由矩形CDEF的面积是矩形BCFA的2倍，且AB=FC=ED，可以得出CD=2BC；其次，由栅栏的总长度为24m，可以用x表示出AB的长度；再次，根据矩形的面积公式“面积=长×宽”和矩形养殖场的总面积为36m2，列出一元二次方程；最后，由于墙的长度为10m，还要对方程的解进行检验，得出正确的答案。

解：（1）∵BC=x，矩形CDEF的面积是矩形BCFA的2倍，

∴CD=2BC=2x。

∴BD=3x。

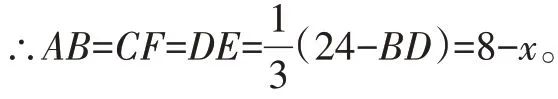
根据题意，得3x（8-x）=36，

解得x1=2，x2=6。

当x=6时，3x=18＞10，不符合题意，舍去。

∴x=2。

答：此时x的值为2。

（2）∵0＜BD≤10，

∴0＜3x≤10。

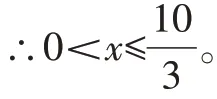
设矩形养殖场的总面积为Sm2。

由（1）得S=3x（8-x）=-3（x-4）2+48。

∵-3＜0，0＜x≤

∴当时，S最大，最大值为

答：当x为时，矩形养殖场的总面积最大，最大值为

【点评】本题考查了一元二次方程和二次函数在几何图形问题中的面积应用。依据数形结合用x表示出矩形的长和宽，以及掌握二次函数的性质是解题的关键。我们要特别注意，二次函数的最值不一定在对称轴x=处取到，应结合实际情况，在自变量的取值范围内求最值。