万变不离其宗——例说二次函数解决矩形面积最值问题

文／周艳

求矩形面积的最值问题是我们比较常见的问题，解决此类问题的关键是什么？如何建立函数模型解决此类问题？希望本文中的例子，能让同学们体会到如何在变化的条件中寻找到不变的方法。

问题1用一根长22cm的铁丝：

（1）能否围成面积是30cm2的矩形？

（2）能否围成面积是32cm2的矩形？

【分析】此题是苏科版数学教材九年级上册第24页的问题1，通过建立两个一元二次方程，从能否解出实数根的角度来解决。现在，学过了二次函数的知识，我们不妨换个思路，尝试通过函数模型解决此类问题。矩形的面积（y）会随着矩形一边（x）的变化而变化。

解：设这根铁丝围成的矩形的长是xcm，则宽为（11-x）cm，矩形的面积为ycm2。

根据题意，得0＜x＜11。

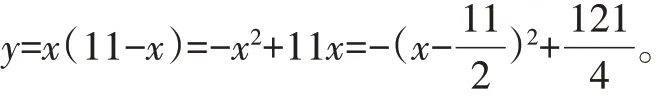
∵a=-1＜0，∴函数图像开口向下。

又∵0＜x＜11，

∴当时

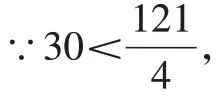
∴能围成面积是30cm2的矩形。

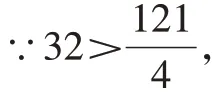
∴不能围成面积是32cm2的矩形。

【总结】本题中存在两个数量关系：矩形周长=2（长+宽）①，矩形的面积=长×宽②。在设长为x后，可以先利用①表示出宽，再利用②表示出面积，建构函数模型，得到二次函数表达式，随后利用配方法求出面积最值，最后结合自变量的变化范围得到面积变化范围，由此判断围成的面积是否在范围内。

此方法对比利用方程的方法，可以减少构建一元二次方程的个数，也较为容易理解。此方法的难点在于同学们能否通过问题情境感知到一个量随着另一个量的变化而变化，从而选择从函数角度来解决问题。

例题如图1，一个矩形菜园ABCD，一边AD靠墙，墙MN长为60m且MN≥AD，另外三边用总长100m的篱笆围成。求矩形菜园ABCD面积的最大值。

图1

【分析】此题的变化有：增加了一面墙，将原矩形的四边长度之和变为三边长度之和；自变量的取值范围要作出适当调整，AB长度的2倍小于篱笆总长，AD（BC）的长度不超过墙的长度。

解：设AB=xm，则BC=（100-2x）m。

解得20≤x＜50。

设矩形的面积为Sm2。

S=x（100-2x）=-2（x-25）2+1250。

∵a=-2＜0，∴函数图像开口向下。

又∵20≤x＜50，

∴当x=25时，S最大值=1250。

∴矩形菜园ABCD面积S的最大值为1250m2。

【变式1】如图2，利用旧墙和篱笆围成中间隔有一道篱笆的矩形菜园ABCD，一边AD靠墙，墙MN长为60m且MN≥AD，篱笆总长100m。求矩形菜园ABCD面积的最大值。

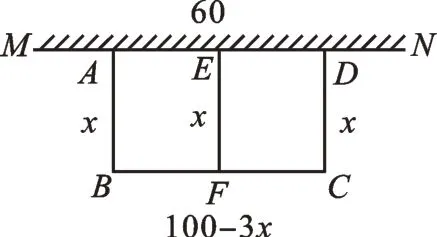
图2

【分析】本题增加了一条边EF，利用例题中的方法，将BC的长度和自变量x的取值范围作出适当调整即可。

解：设AB=xm，则BC=（100-3x）m。

设矩形的面积为Scm2。

∵a=-3＜0，∴函数图像开口向下。

又∵

∴当时

∴矩形菜园ABCD面积S的最大值为

【变式2】如图3，一个矩形菜园ABCD，一边AD靠墙，墙MN长为40m且MN≥AD，一边BC上留有一个2m的门，另外三边用总长100m的篱笆围成。求矩形菜园ABCD面积的最大值。

图3

【分析】本题做了两个改变：（1）增加了一个2m的门，有的同学会认为，门占了篱笆的长度，篱笆变成了98m。其实，篱笆的长度100m没有任何改变，因为加了门，矩形菜园的三边之和变为AB+BC+CD=（100+2）m。（2）墙的长度由60m变为40m，影响自变量x的取值范围。

解：设AB=xm，则BC=（100+2-2x）m。

解得31≤x＜51。

设矩形的面积为Scm2。

∵a=-2＜0，∴函数图像开口向下。

∵当31≤x＜51时，S随x的增大而减小。

∴当x=31时，S最大值=1240。

【总结】本题中二次函数的顶点横坐标x不在x的取值范围31≤x＜51中，所以顶点的纵坐标不是本题的最大值。我们可以利用表达式画出草图（如图4）来思考，在求出特殊点的坐标后，直接得出最值。

如图4，当x=31时，S最大值=1240。

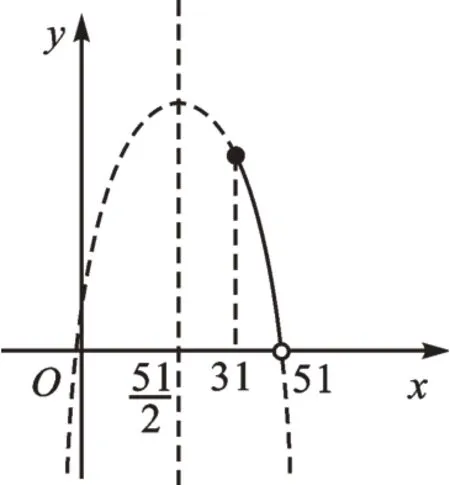
图4

【变式3】如图5，一个矩形菜园ABCD，一边AD靠墙，墙MN长为am且MN≥AD，另外三边用总长100m的篱笆围成。求矩形菜园ABCD面积的最大值。

图5

【分析】此题将墙的长度由具体的60、40转变成了字母，体现从特殊到一般。通过以上题目的训练，同学们应该能感受到墙的长度主要影响的是自变量x的取值范围，从而明确了最值的情况不外乎有两种：①顶点横坐标在取值范围内，则可将顶点的纵坐标直接作为本题最大值；②顶点横坐标不在取值范围内，则需要根据函数的增减性（或结合图像）来判断最值情况。

解：设AB=xm，则BC=（100-2x）m。

设矩形的面积为Scm2。

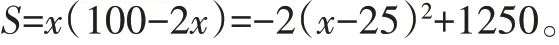
∵a=-2＜0，∴函数图像开口向下。

①当，即a≥50时，取x=25，S最大值=1250。

②当，即0＜a＜50时，因 为随x的增大而减小，所以取x=

综上所述：当a≥50时，S最大值=1250；当0＜a＜50时

【归纳总结】通过以上几题，同学们应能发现解决此类问题需要抓住的主要步骤为：根据数量关系确定自变量，再表示出矩形的面积（应变量），建立二次函数表达式。在整个过程中，我们一定要养成写出自变量取值范围的好习惯。就本类题型而言，主要考虑垂直于墙和平行于墙的两条线段的实际意义，列出不等式组，确定自变量的范围。最后，我们再结合自变量的取值范围，看二次函数的顶点横坐标是否在自变量取值范围内，得到正确的最值。