基于PSO-CNN的深部找矿预测模型构建

罗 杰, 周仲礼, 邹天一, 刘 斌, 龚 灏

(1.成都理工大学 数理学院,成都 610059；2.数学地质四川省重点实验室,成都 610059)

近年来，中国在矿产资源勘探方面取得了一系列成果，但矿产资源不足问题依然严峻，未来很长一段时间内对国外矿产资源依存度仍然很高[1-2]。随着对矿产资源持续的大规模开采，使得地表矿、浅部矿趋于消耗殆尽，深部找矿已经成为当前实现资源增储的必然趋势[3-4]，但深部找矿存在信息少、难度大、投资多、风险大等难题[5]。因此，越来越多的专家通过开展三维地质建模，将海量、多源、异构、多尺度的地质大数据进行充分挖掘、有效提取和融合集成，更直观地展示地质体空间形态以及相互关系，进而获得更为准确的矿产预测结果[6-7]。

成矿预测是以科学预测理论为指导在掌握有限信息的条件下制定最优决策的工作，是实现科学找矿、扩大资源储量的重要途径和方法。但是由于控矿因素的隐蔽性和矿床成因的复杂性，导致成矿预测的结果往往具有不确定性，因此，探寻成矿预测结果的准确性一直是学者们的研究热点[8-9]。经过几十年的发展，随着成矿预测理论的不断完善，预测成矿远景区的方法也逐渐增多，如秩相关分析法、证据权重法、找矿信息量法、机器学习等[10]。吴颖慧[11]运用秩相关系数法分析研究区各预测要素，构建了特征分析法的预测模型，最终成功确定了多个预测区。王江霞等[12]将GIS技术与证据权重法相结合，成功地对冀东地区沉积变质型铁矿资源进行了预测。何海洲等[13]在分析了研究区成矿规律的基础上选取找矿标志，利用找矿信息量法成功地对研究区圈定成矿靶区。陈进等[14]构建了三维矿体模型，并将随机森林(RF)算法引入成矿预测领域，对大尹格庄金矿的预测取得了不错的效果。

随着大数据时代的到来，将大数据的理念和方法应用于成矿预测领域是一项很有意义的探索[15-16]。其中，机器学习作为大数据分析的一种重要方法，在自然语言处理、图像识别、情感分析、智能机器人、数据挖掘等领域都有着广泛的应用，现已成为矿产资源预测的前沿热点[17-18]；随机森林、支持向量机、K-近邻算法、人工神经网络等机器学习算法也被广泛应用于矿产资源预测中[19]。深度学习作为机器学习的一种，是一类具有多隐藏层的机器学习模型。在深度学习中，卷积神经网络(convolutional neural networks，简称CNN)算法是一种高效的识别方法，近年来在语音识别、图片分类、人脸识别等问题上均有突破[20]，并被尝试运用于成矿预测中，建立成矿特征与矿体间的非线性关系[21]。蔡惠慧等[22]利用一维CNN挖掘研究区综合成矿信息并成功圈定了成矿远景区。参数的选择对CNN模型性能有很大影响，参数的优化不仅可以提高数据特征提取能力，还对预测结果有直接影响。但在目前的研究中，模型训练大多凭借经验手动调参，导致计算代价大且难以得到满意的效果，如何高效地优化参数已成为构建CNN模型的重点。对于CNN模型参数的优化，现有很多方法，如贝叶斯优化[23]、粒子群算法(particle swarm optimization,简称PSO)[24]、多策略蝠鲼觅食优化算法(multi-strategy manta ray foraging optimization，简称MSMRFO)[25]、进化算法(evolutionary algorithm,简称EA)[26]。其中，PSO是由Eberhart和Kennedy提出的一种优化算法[27]，该算法具有收敛速度快、控制参数少、收敛能力强等优点。已有研究表明通过使用PSO算法对CNN模型参数进行优化，优化后的CNN模型在性能上有较大的提升[28]。

西藏冈底斯成矿带矿产具有种类多、储量大、优势矿种明显、勘查程度低、找矿前景大等特点。而雄村斑岩型铜金矿集区作为西藏冈底斯成矿带的大型铜金矿集区之一，具有良好的找矿前景[29-30]。本文以冈底斯成矿带上的雄村斑岩型铜金矿床Ⅱ号矿体为研究对象，在构建三维地质体模型的基础上，通过提取多元找矿信息，结合PSO-CNN算法建立三维深部找矿预测模型，并讨论数据集对模型的影响，验证模型的有效性，进而为深部找矿提供方法技术支撑。

1 基于PSO-CNN的成矿预测框架构建

本文针对深部找矿预测问题，在地质大数据时代背景下，结合深度学习(PSO-CNN)，构建了如图1所示的研究框架，具体包括以下5个步骤：①收集研究区的地质、地球化学等相关数据；②采用空间插值方法，构建地质体三维块体模型；③采用随机划分方式，将数据集分为训练集(70%)与验证集(30%)；④构建基于PSO-CNN预测模型，通过PSO算法对CNN模型的超参数进行优化来提升模型性能，并以预测准确率、AUC(area under curve)等指标对模型效果进行评估；⑤验证模型的有效性，将PSO-CNN模型与找矿信息量模型进行对比分析，验证PSO-CNN模型相比于找矿信息量模型在成矿预测方面的优越性。

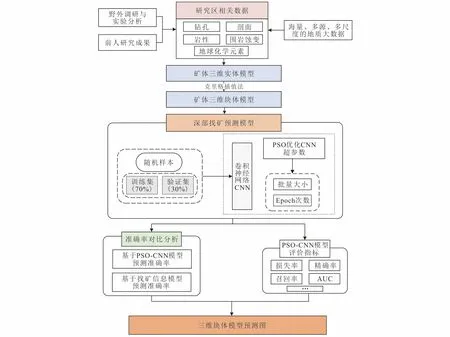
图1 研究过程框架图Fig.1 Research framework diagram

1.1 研究区地质背景

冈底斯成矿带位于青藏高原拉萨地体南缘，雄村矿床处于冈底斯成矿带上，其南侧紧邻日喀则弧前盆地，是冈底斯成矿带南缘重要的斑岩型铜(金)矿床。目前，雄村矿区已发现3个(Ⅰ号、Ⅱ号、Ⅲ号)大型铜金矿体，矿区内金属储量巨大，显示出良好的资源开发潜力和找矿前景[31-33]。本文以雄村矿区的Ⅱ号矿体为研究对象，共收集了8个剖面、34个钻孔数据(图2)。

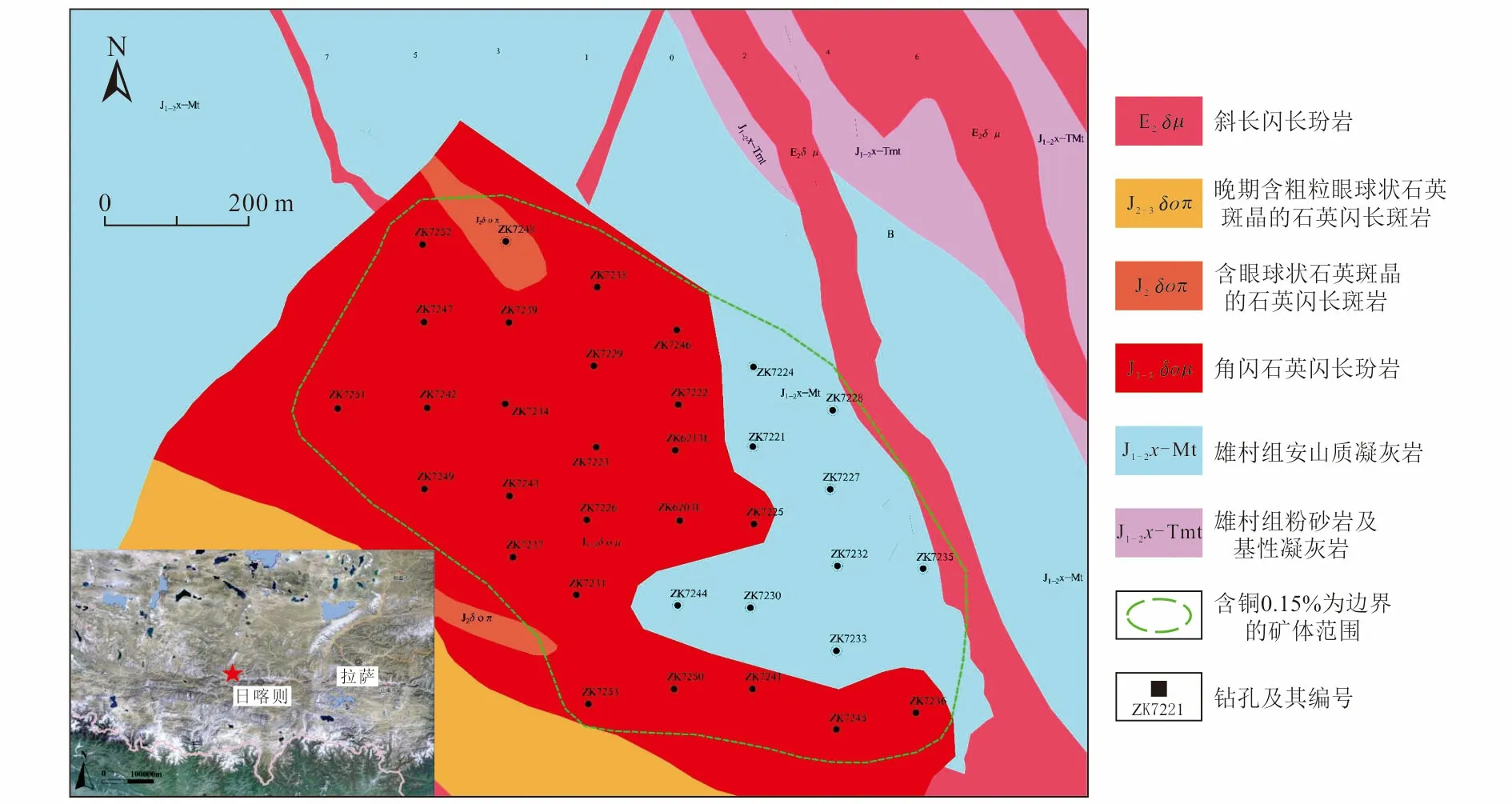
图2 雄村矿区Ⅱ号矿体地质简图Fig.2 Simplified geological map of No.Ⅱ ore body in Xiongcun metallogenic area

1.2 成矿有利信息提取及三维建模

本文主要利用Micromine11.0软件构建地质体三维模型。基于雄村Ⅱ号矿体钻孔、剖面等数据资料，对地质体进行圈定，建立地质体三维实体模型和块体模型。三维地质实体模型能很好地展现各地质体三维形态，但要定量分析矿体和相关地质体则需要借助块体模型[34]。其中，三维块体模型是整个三维建模的核心，本文按X-Y-Z方向选定块体标准规模为5 m×5 m×5 m，共划分为 4 562 577个小块体(矿体小块体数量为 1 126 391个)。雄村Ⅱ号矿体三维块体模型如图3所示。

图3 矿体三维模型Fig.3 Three-dimensional model of ore body

根据前人研究成果，提取以下找矿信息：①岩性，Ⅱ号矿体在平面上为一巨型透镜体，呈北西-南东走向，Ⅱ号矿体的形态、产状主要受中-晚侏罗世侵位的角闪石英闪长玢岩及其含矿围岩控制。②地球化学特征，矿化组合通常以Cu、Au为主，伴有Ag、Mo、Pb、Zn矿化，而成矿元素的分带性不明显，Cu、Au以及Mo、Ag一般在矿体中部富集，Pb、Zn含量很低，一般分布在矿体的外侧。Au、Ag、Cu元素在研究区具有明显富集的趋势，表明它们具有比较好的成矿潜力。③围岩蚀变，地表常见的是青磐岩化、黄铁绢云岩化、早期钾硅酸盐化蚀变和钙化-钠化-钾化、强硅化蚀变，与成矿作用相关的蚀变主要为钾硅酸盐化，而钾硅酸盐化蚀变普遍遭受其他蚀变类型不同程度的叠加，同时矿体上方的地表周围铁染现象普遍可见[35-36]。提取的找矿信息见表1。

表1 找矿模型要素[36]Table 1 Elements of prospecting-information model

2 基于PSO-CNN的成矿预测模型构建

2.1 算法原理

2.1.1 PSO算法原理

PSO算法是通过研究鸟群觅食行为提出的一种优化算法，其基本思想来源于人工生命和演化计算理论，通过群体中个体之间的协作和信息共享来寻求最优解。本文基于PSO算法的CNN超参数确定流程如图4所示。

图4 粒子群算法流程图Fig.4 Flow chart of particle swarm optimization

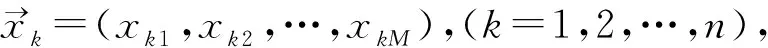
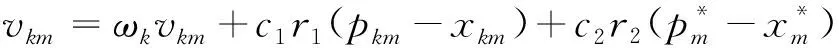
(1)

xkm=xkm+vkm

(2)

其中：k=1,2,…,n；m=1,2,…,M；ωk为惯性因子；c1与c2(c1,c2≥0)为学习因子；r1与r2为属于区间[0, 1]之间的随机数；vkm∈[-vmax,vmax],vmax为给定的一个常数。

2.1.2 CNN算法原理

CNN是一类具有深度结构的前馈人工神经网络，一般由输入层、卷积层、池化层、全连接层及输出层构成[37]。

a.卷积层

卷积层是CNN的基础，通过卷积运算减少了CNN所需要的参数。卷积层通过权值共享和局部感知获得图像的特征，卷积层以“卷积核”为中介，卷积核可视作一种特殊的神经元，有着自定大小的权值矩阵；权值共享是指同一个卷积核的参数在整个图像内是共享的；局部感知指的是卷积核通过对局部数据进行卷积计算进而减少神经元连接的数目。进行卷积运算就是提取数据特征的过程，每个卷积核进行卷积运算都提取一种特征。卷积层的计算公式如下

(3)

式中:xj代表输入数据的元素；kij代表卷积核的元素 ；f()代表激活函数；k代表卷积核；l代表卷积层数；M是输入层的感受野；b代表每个输入图的一个偏置值[38]。

b.池化层

CNN通常在连续的卷积层之间周期性地插入一个池化层。池化过程实际是一个降采样过程，常见的池化方式有最大池化和平均池化——池化层将输入特征图切成几个区域，取每个区域的最大值或平均值。池化层在保留了图像显著特征的同时使图像尺寸变小，减少了CNN模型所需要的参数以及简化了模型的复杂度，还能有效控制过拟合，提高训练效率，具有很强的鲁棒性。

c.全连接层

CNN网络经过若干个卷积层、池化层后会接入一个全连接层，该层的每一个神经元与前一层的所有神经元互相连接，同层神经元之间不连接，该层的作用是把所有的局部特征结合成全局特征，在CNN网络中起到分类的作用。

2.2 数据集划分

根据提取的找矿信息，按照同样的尺度并采用克里格(Kriging)插值法进行属性数据插值[39]，形成三维块体模型，进而形成多属性立方块模型，为后面的模型预测提供基础数据源。研究表明，含矿单元数与非含矿单元数为1∶1时，得到的CNN训练模型效果最优；因此，本次选取 1 126 391个有矿块体与 1 126 391个无矿块体作为数据集，将数据集随机分成两个互斥的集合——训练集(70%)和验证集(30%)，用于后面PSO-CNN模型的训练与预测[40]，划分示意图如图5。

图5 数据集划分示意图Fig.5 Data set partitioning diagram

2.3 模型评价指标

预测与真实分类间的组合关系如表2所示，主要选取准确率、精确率、AUC等指标对模型进行评价。

表2 混淆矩阵Table 2 Confusion matrix definition

准确率(accuracy)表示模型预测正确的样本数与总样本数之比；精确率(precision)表示正确预测正类样本数量和预测正类样本总数量之比；召回率又称真阳率(true positive rate)，表示正确预测正类样本数量与全部正类样本数之比，与之相对应的为假阳率(false positive rate)。准确率(A)、精确率(P)、真阳率(RTP)、假阳率(RFP)的计算公式如下

A=(PT+NT)/(PT+NF+PF+NT)

(4)

P=PT/(PT+PF)

(5)

RTP=PT/(PT+NF)

(6)

RFP=PF/(PF+NT)

(7)

式中：PT为模型分类为正的正样本；PF为模型分类为正的负样本；NT模型分类为负的负样本；NF为模型分类为负的正样本。

ROC曲线是描述分类器的RTP与RFP之间的变化关系。ROC曲线下方的面积被称为AUC，AUC值越高，也就是曲线下方面积越大，说明模型预测的性能越好。

2.4 基于PSO的CNN参数确定

2.4.1 待优化的超参数

本文构建PSO-CNN算法网络模型进行深部成矿预测。在PSO算法优化CNN参数前，首先要确定的是要优化的超参数。参数的选择对模型效果至关重要，本文选取CNN模型中两个至关重要的参数进行优化：批量大小(λ)与Epoch次数(μ)。将这两个参数作为PSO算法的优化对象，建立一个二维的超参数优化空间。在空间中的每个粒子的位置信息xk可以表示为

xk=(λk,μk)

(8)

本文2个超参数的搜索范围如表3所示。

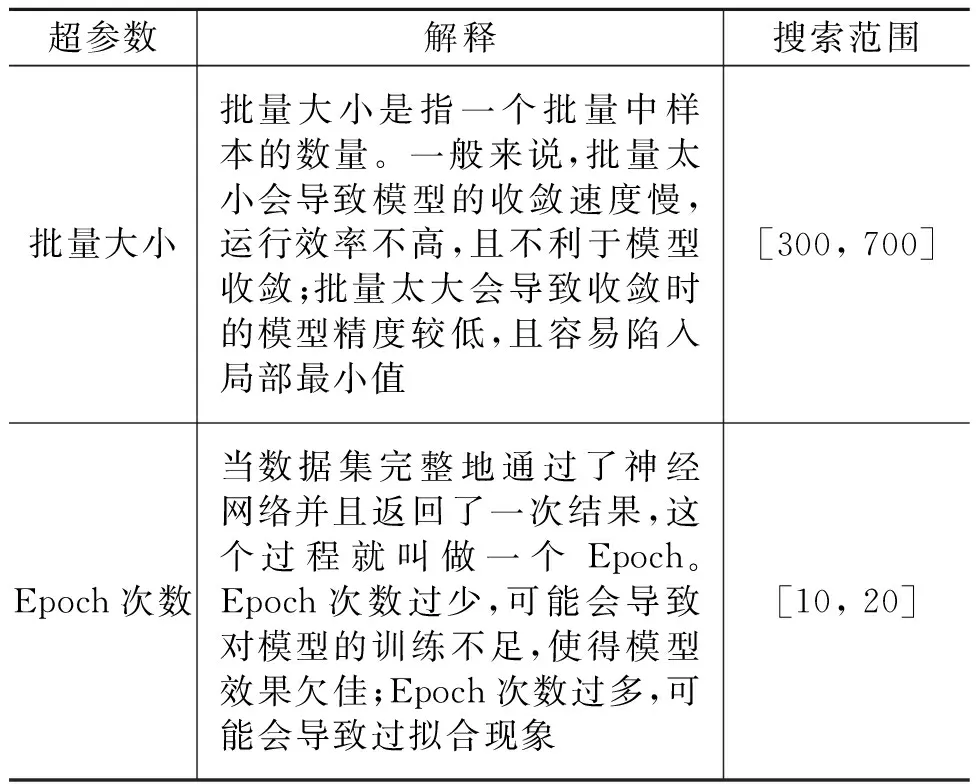
表3 CNN超参数的搜索范围Table 3 The search scope of the CNN hyperparameter

2.4.2 最优超参数的求解

粒子群算法中主要有5个参数需要确定：惯性因子、粒子特征数、最大迭代次数、自身认知学习因子、群体认知学习因子。这些参数的具体设置如表4所示。

表4 粒子群算法的参数设置Table 4 Parameter settings for the particle swarm optimization

本文构建了一个1层输入层、4层卷积层、2层池化层、1层输出层的CNN模型。其中输出层包含2个神经元，分别是0(无矿)、1(有矿)。将成矿预测因子作为输入，是否有矿作为输出，同时运用粒子群算法，对上面提及的CNN模型的2个超参数为优化超参数，以CNN模型的准确率作为粒子(超参数组)的适应值，设置5个粒子，进行5次迭代，记录每次迭代得到的最优适应值。每次迭代的最优准确率及其对应的超参数组合见表5。

表5 PSO-CNN模型的迭代过程Table 5 The iterative process of the PSO-CNN model

从表5可以看出最优适应值对应的最优超参数组合是(337,19)。确定最优超参数组合后，将数据再次输入由最优超参数组合确定的CNN模型中，经过训练后模型的评价指标如图6所示，损失率低至23.71%，精确率、召回率、AUC分别高达96.40%、89.53%、96.54%，并有着较好的收敛性。上述实验结果表明PSO-CNN模型相对已有的数据来说是可靠的，可以通过优化后的PSO-CNN模型提取到数据较充分、全面的本质特征，进一步说明PSO-CNN模型在深部成矿预测领域也能取得较好的效果。

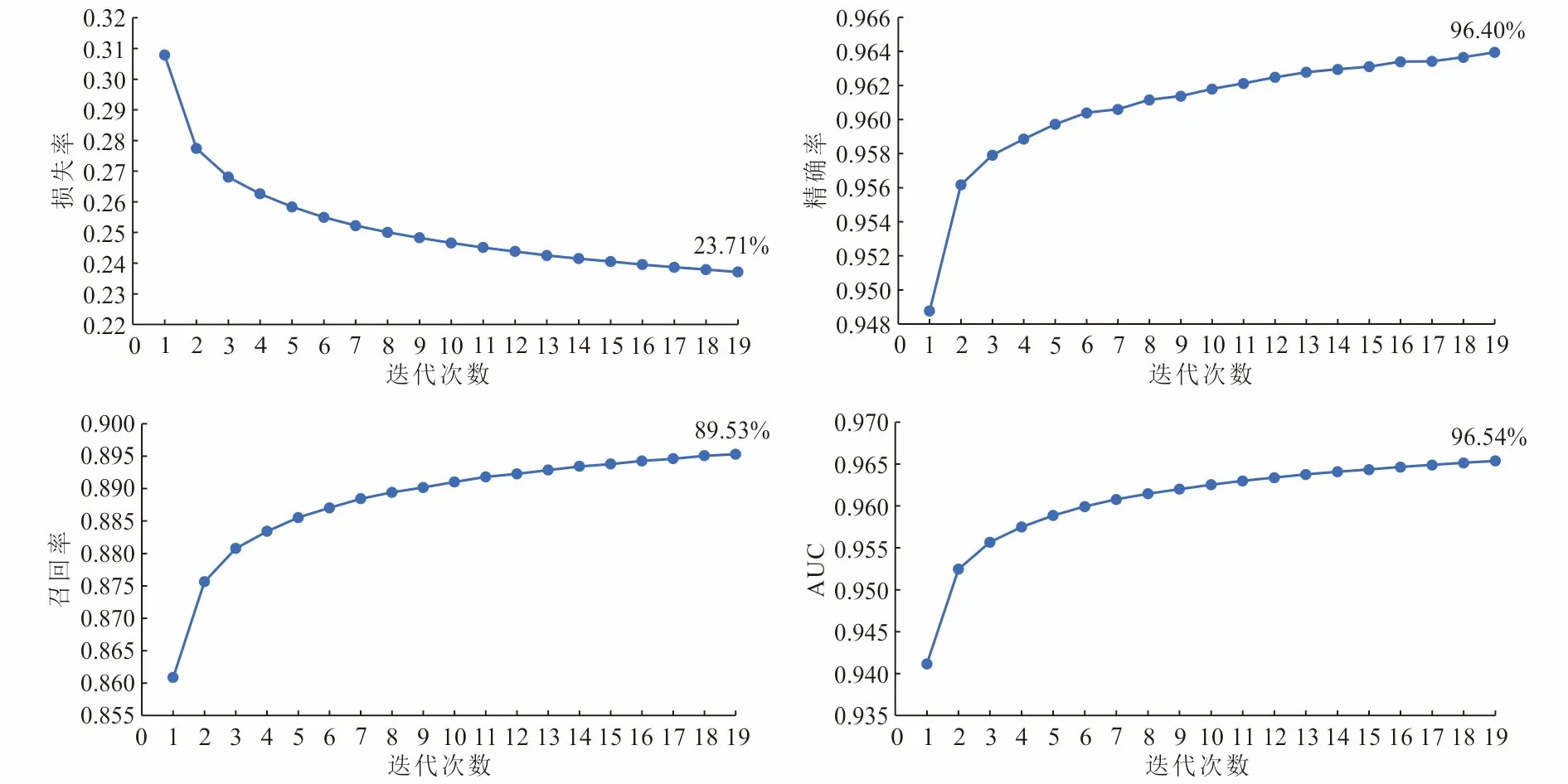
图6 CNN模型评价指标结果Fig.6 The evaluation index results of CNN model

3 算法预测结果分析

3.1 结果分析

为了证明基于PSO-CNN深度学习模型在成矿预测性能上的有效性，本文将PSO-CNN模型的预测结果与已知矿体进行拟合。如图7所示，PSO-CNN模型预测结果与已知矿体的拟合度较高，一定程度上显示出PSO-CNN模型在成矿预测方面具有良好的效果。

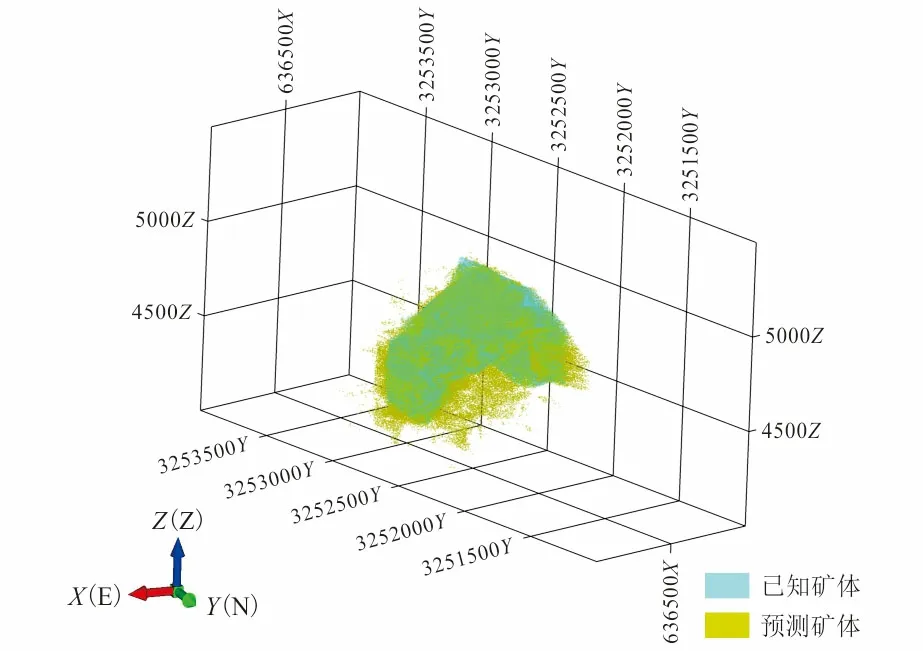
图7 预测结果拟合图Fig.7 Fitting diagram of prediction results

3.2 对比分析

为突出PSO-CNN模型在成矿预测领域上的优越性，本文构建找矿信息量预测模型，将两者的预测准确精度进行对比分析。为建立找矿信息量预测模型，本文通过成矿有利信息分析并提取确定了7个有利找矿标志，运用找矿信息量法计算了各有利找矿标志信息量值(表6)。找矿信息量计算公式如下

(9)

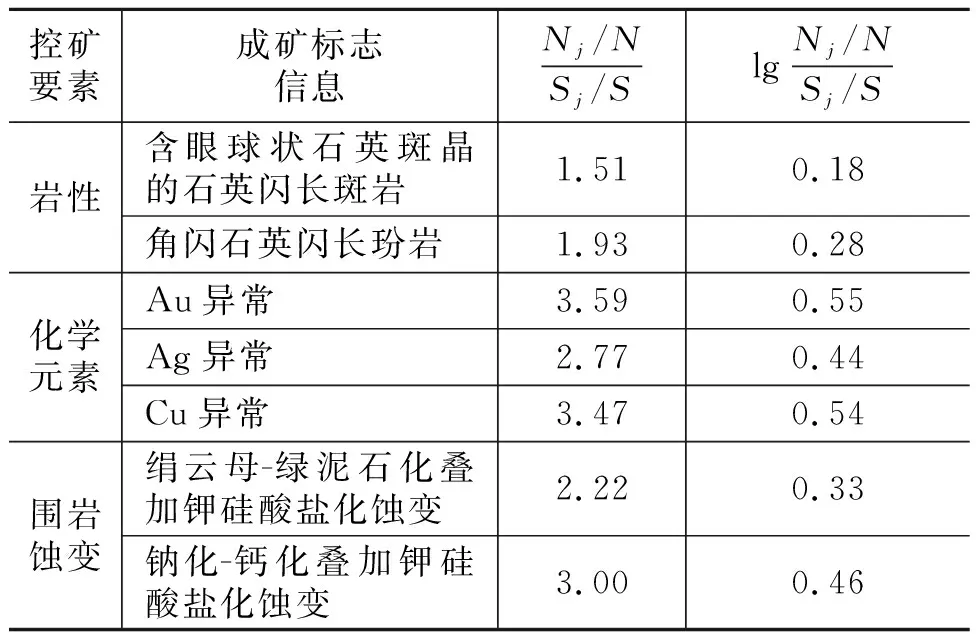
表6 各变量信息量表Table 6 Information scale of each variable

式中：IA(B)为A标志出现时含有B矿的可能性大小；Nj为研究区内具有找矿标志A的含矿单元数；N为研究区内含矿单元数；Sj为研究区内具有找矿标志A的单元数；S为研究区内单元总数[41]。

从找矿信息量图(图8)中可以看出，随着信息量的增大，满足条件的矿体数减少，而含矿率却逐渐增大，说明有利于成矿的立方块单元正逐渐被搜寻出来，这证明了用信息量法找矿的可行性。选取成矿有利区信息量的临界值为0.3(矿块数与含矿率交点处)，成矿有利区内信息量>0.3的有矿单元共 812 808个，可知综合成矿有利区内预测准确率为0.721 6。

图8 雄村矿集区Ⅱ号矿体信息量图Fig.8 The information scale diagram of Xiongcun No.Ⅱ ore body

由表7可看出，基于PSO-CNN模型的预测准确率更高，结果更具有说服力，PSO-CNN模型与找矿信息量模型相比具有更好的预测性能。

表7 预测结果准确率Table 7 Accuracy of prediction results

4 结 论

本文针对地质大数据背景下的深部成矿预测问题，结合深度学习理论，充分挖掘数据的空间特征，构建深部成矿预测模型，取得的主要结论如下：

a.以冈底斯成矿带上的雄村斑岩型铜金矿床Ⅱ号矿体为研究对象，构建了一种基于PSO-CNN的隐伏矿体三维预测方法，从预测评价指标来看，精确率和AUC分别为96.40%、96.54%，表明PSO-CNN模型在成矿预测方面能取得较好的效果。

b.将PSO-CNN模型与找矿信息量模型的预测结果进行对比分析，表明本文构建的PSO-CNN模型在预测准确率上有着更好的效果，同时，结合三维可视化结果，说明基于PSO-CNN构建的成矿预测模型具有良好的可行性。

c.本文建立的PSO-CNN网络预测模型通过多层网络的特征学习，能够提取到更充分、全面的本质特征，从而得到了较好的预测效果。但信息提取还不够全面，缺乏深部地球物理等方面的数据，后续的研究将收集更多的相关数据来验证所构建的预测模型。此外，在优化模型参数方面还存在提升的空间(如隐藏层数、神经元个数等)，后续的研究工作将进一步深入，充分发挥深度学习在深部成矿预测中的优越性。