灌区分布式多水源时空优化配置

刘 巍，雷 波，廖晋一，杜丽娟

灌区分布式多水源时空优化配置

刘 巍1,2，雷 波1,2※，廖晋一3，杜丽娟1,2

（1. 中国水利水电科学研究院水利所，北京 100048；2. 中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京，100048；3. 安徽理工大学信息与测绘工程学院，淮南 232001）

为充分考虑灌区多水源供需水时空分布不均问题，该研究以河北省邯郸市漳滏河灌区为例，通过遥感技术反演土壤含水率并计算不同生育期的土壤水分修正系数，进而计算各子单元的作物需水量；分别以水库配水缺水量最小、灌区效益最大作为配置目标建立灌区分布式多水源优化配置模型，计算并分析9种水文情景下（蓄水高值-降水丰值、蓄水高值-降水平值、蓄水高值-降水枯值、蓄水中值-降水丰值、蓄水中值-降水平值、蓄水中值-降水枯值、蓄水低值-降水丰值、蓄水低值-降水平值、蓄水低值-降水枯值）配水量的时空分布规律。结果表明：通过遥感反演并模拟得出的灌区土壤含水率空间分布符合灌区实际土壤情况；漳滏河灌区4—8月的累计需水量最大，占全年总需水量的76.8%；不同情景下，民有分区的配水量均高于滏阳河分区，且空间分布变化规律明显；为保证灌区的经济效益，应优先选择水价较低、单位面积配水量较高的引黄水作为主要外调水源。研究结果可为灌区水资源时空配置及水资源高效管理提供新思路。

时空分布；土壤含水率；降水；灌区；多水源；农业水资源；优化配置

0 引 言

水资源是粮食生产必不可少的投入要素，是保证粮食安全的战略物资[1]。随着社会不断发展，水资源的需求量逐渐增长，加之环境污染、气候变化等问题使得水资源的供需矛盾日益凸显[2-3]。中国是农业大国，土地资源丰富，但水资源时空分布不均问题导致单位面积的供需水量不平衡，水土资源难以发挥最大效益[4-6]。因此，在当前水资源日益紧缺的局面下，如何优化水资源的时空配置，提升农业生产的最大效益是保证粮食安全及农业经济可持续发展的关键问题[7-10]。

灌区是农业生产的重要基地，也是组成灌溉系统的基本要素。灌区水资源优化配置是通过合理调控供水量、调整种植面积等方式以满足灌区效益、水量平衡、环境可持续发展等目标的决策方法[11-14]。随着灌区水资源优化配置研究的不断丰富，研究者们从多角度提出了灌区水资源优化配置方法。例如，付强等[15]针对灌区多水源特点，以及作物在不同生育期的水分敏感程度，以黑龙江省和平灌区水稻不同生育期的灌溉水资源优化配置作为实例研究，该模型在保证产量的同时，提升了灌区的灌溉水利用系数。李茉等[16]从水循环角度，建立了灌区多水源优化配置模型，通过和平灌区的实例验证，灌区水分生产率可提升11%。Brown等[17]针对季节性缺水问题建立了一种适用农场的逐日灌溉水优化配置模型以满足效益最大化。随着研究角度的不断延伸，不同理论的融入使得灌区水资源优化配置模型的研究更为系统，而水源时空分布问题对水资源优化配置结果影响的研究仍有不足。由于灌区水源时空分布不均、土壤类型及种植结构差异等问题，致使以往的水资源优化配置模型难以在时空上最大限度地达到供需水平衡，限制灌区用水效率的进一步提升[18-20]。因此，综合考虑灌区水源分布特点及不同生育期土壤水分变化情况，对灌区进行时空水资源优化配置更符合实际的配水需求，可避免由渠首控制整个灌区配水而导致灌区配水不均、排水量大、灌溉水利用效率低等问题[21-22]。基于此，本研究以河北省邯郸市漳滏河灌区为例，建立了考虑土壤含水率、水源及作物种植结构时空分布特点的灌区分布式多水源优化配置模型，以期为灌区多水源时空优化配置提供理论与技术参考，提升灌区水资源的最优化管理。

1 研究区域与方法

1.1 研究区域概况

漳滏河灌区位于河北省邯郸市中部，地处半湿润半干旱区，呈西南高、东北低的地形趋势，由滏阳河分区和民有分区构成，总控制面积3.48×105hm2。主要种植冬小麦、棉花和玉米。年均蒸发量1 120 mm，年均降水量580 mm。灌区水源包括水库水、南水北调水和引黄水，其中，东武仕水库和岳城水库为灌区的首选水源，其水价低、管控方便；南水北调水和引黄水作为外调水源以缓解用水高峰时的缺水问题。为了便于灌区用水管理，综合考虑水源供水关系、渠系之间水力联系等因素，将漳滏河灌区划分17个子单元，分别为：滏阳河分区的F01、F02、F03、F04、F05、F06、F07和民有分区的M01、M02、M03、M04、M05、M06、M07、M08、M09、M10（图1a）；其中，东武仕水库供水子单元包括：F01～F07，岳城水库供水子单元包括：M01～M10，南水北调供水子单元包括：F01～07、M01～M06、M08～M09，引黄供水子单元包括：M07、M10（图1b）。

注：F01～F07为滏阳河分区子单元；M01～M10为民有分区子单元。

1.2 研究思路

本研究通过遥感技术获取灌区种植面积、土壤含水率等数据，以水库配水的缺水量最小和灌区配水效益最大分别作为目标函数建立灌区分布式多水源优化配置模型。研究技术路线见图2。

图2 研究技术路线图

1.3 需水量计算

该研究采用联合国粮农组织推荐的作物系数法估算作物需水量，该方法根据作物在自然条件下需水量受温度、湿度、土壤水分和作物长势等因素的影响程度，计算基础作物系数和土壤水分修正系数，进而结合通过彭曼公式（Penman-Monteith）计算出的参考作物蒸散发量，得出作物需水量。公式[23]如下：

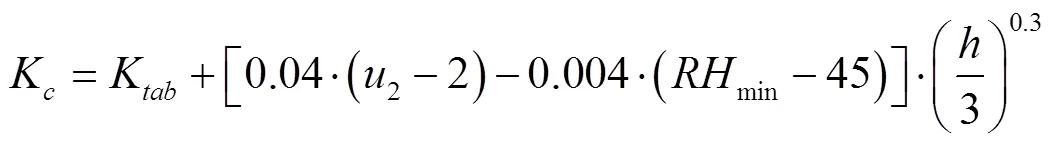
式中为作物需水量，mm；K为土壤水分修正系数；K为基础作物系数；0为日参考蒸散量，mm；R为作物表面的净辐射量MJ/m2；为土壤热通量，MJ/(m2·d)；Δ为饱和水汽压与温度的关系曲线斜率值，kPa/℃；是湿度计常数，kPa/℃；为日平均气温，℃；2为2 m高地面的日平均风速，m/s；e为空气饱和水汽压，kPa；e为实际水汽压，kPa/℃；K为FAO-56推荐的标准状况下的作物系数；min为日均最小相对湿度，%；为研究期作物麦的株高，m。

1.4 土壤水分修正系数反演与计算

1.4.1 土壤含水率反演

因地表光谱特征与土壤含水率之间存在密切联系，因此，可通过两者之间的关系建立基于地表光谱特征的土壤水分监测模型[24]。本研究利用植被冠层和裸地在近红外波段和红光波段的光谱特征，反演获取垂直干旱指数（Perpendicular Drought Index，PDI）[25-28]，建立PDI与实测土壤含水率之间的关系模型，进而计算灌区的土壤含水率。公式如下：

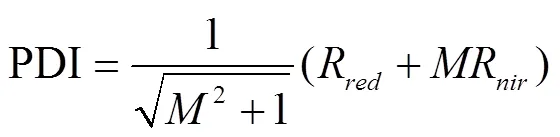
式中R为近红外波段反射率；为土壤线斜率；R为红光波段反射率；I为土壤线在纵坐标上的截距；为PDI与土壤含水率之间的关系模型，为通过模型得出的土壤含水率，%。

1.4.2 土壤水分修正系数

土壤水分修正系数是宏观根系吸水模型的重要组成部分，主要用于反映土壤水分胁迫对根系吸水的抑制作用[29]。公式如下：

式中θ为凋萎含水率，%；θ为田间最大持水率，%。

1.5 优化配置模型

本节建立的灌区分布式多水源优化配置先后以水库配水缺水量最小和经济效益最大作为模型的目标函数。通过一阶段模型获取首选水源的缺水量值，将其作为二阶段模型的约束条件，进而通过二阶段模型决策出外调水源的最优配水量及灌区的最大效益值。该模型通过分布式的方法避免了多目标之间的矛盾，更符合灌区首选水源和外调水源的配水顺序。

1.5.1 一阶段模型

1）目标函数

灌区的首要目标是保障作物的正常生长，要在供水工程允许的条件下尽可能满足作物需水要求。一阶段模型中，以作物需水量与首选水源配水量差值最小，即水库配水缺水量最小为目标，具体如下：

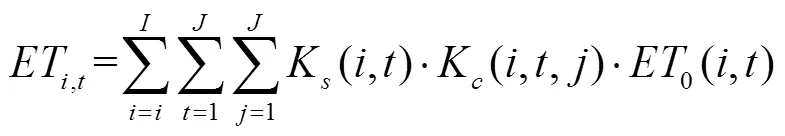
式中为一阶段水库配水缺水量，m3；ET,t为第子单元第时段需水量，m3；x,t为第子单元第时段水库配水量，m3；η为第子单元灌溉水利用系数；K(,)为第子单位第时段的土壤水分修正系数；K(,,)为第子单元第时段作物的作物系数；0(,)为第子单元第时段参考作物蒸散发量，m3；为子单元数量；为时段数；为作物种类数量。

2）约束条件

在一阶段模型中，主要针对首选水源、作物需水量以及渠道输水能力进行约束。具体如下：

①水库水量平衡约束。

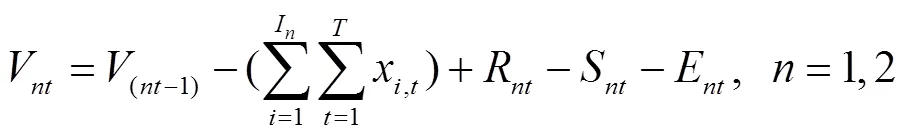
式中V、(nt-1)分别为第、(-1)时段2个水库各时段的蓄水量，m3；R为第时段岳城水库和东武仕水库入库水量，m3；S为第时段2个水库的渗漏量，m3；E为第时段2个水库蒸发水量，m3；W为2个水库的取水许可量，m3；为水库数量，1代表东武仕水库，2代表岳城水库。其中，水库渗漏损失按计算时段平均蓄水量的1%计算，满足如下方程：

②需水量约束

式中A为第子单元的作物灌溉面积，hm2；P,t为第子单元第时段有效降水量，mm。

③水库库容约束

式中MinVMaxV分别为2个水库的死库容、总库容m3。

④渠道输水能力约束

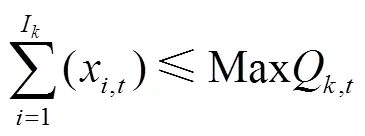
式中MaxQ,t为输送水库水的第渠道第时段最大输水能力，m3；I为负责为子单元输送水库水的条渠道。

⑤非负约束

模型涉及的变量包括：作物需水量、灌溉水利用系数、水库蓄水量、水库取水许可量、水库渗漏量、水库蒸发量、渠道最大输水能力、死库容、总库容等均为非负值。

1.5.2 二阶段模型

1）目标函数

灌区的经济效益是管理部门和农户关注的重点，主要取决于作物的产量及成本、水源供水量及水价。在二阶段模型中，通过优化配置外调水源的配水量，以保证灌区的经济效益最大。具体如下：

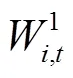
2）约束条件

在二阶段模型中，主要针对缺水量和外调水源的渠道输水能力进行约束。其中，缺水量约束是将通过一阶段模型得出的水库配水缺水量作为二阶段模型的约束条件，即外调水源的配水量之和不超水库配水缺水量。具体如下：

①缺水量约束

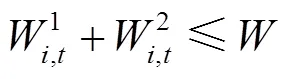
②渠道输水能力约束

式中MaxQ,t为输送外调水源的第渠道第时段最大输水能力，m3；I为子单元输送外调水的条渠道。

3）非负约束

模型中涉及的变量，包括：粮食作物产量、粮食作物价格、水库水价、引黄和南水北调水水价，粮食作物成本及南水北调和引黄配水量等均为非负值。

1.6 方案设置

灌区的配水量受来水情况影响，根据漳釜河灌区资料显示，外调水源的取水量较小，不受来水频率限制，因此，仅设置了水库蓄水量和降水量的来水频率，即水库蓄水量高、中、低和降水量丰、平、枯的9种组合情景，见表1。

表1 不同水文情景信息表

注：V代表水库蓄水量、P代表降水量；V和P的累计频率划分区间分别为25%、75%；VH、VM、VL分别代表水库蓄水量高、中、低；PH、PM、PL分别代表降水量丰、平、枯。

Note: V is the storage capacity of the reservoir and P is the precipitation; The cumulative frequency division of V and P are 25%, 75%；VH, VM and VL represent high, medium and low reservoir water storage respectively. PH, PM and PL represent abundant, flat and dry precipitation respectively.

2 结果分析

2.1 土壤水分修正系数结果

遥感数据采用美国地质勘探局Sentinel -2A光学遥感影像（https://earthexplorer.usgs.gov/）。综合考虑作物主要生育期及遥感影像可利用度，选取2020年1月8日（冬小麦-越冬期）、4月27（冬小麦-快速发育期及生育中期；棉花-初始生长期）、6月8日（冬小麦成熟期；玉米-快速生长期；棉花-快速发育期）、8月4日（棉花-快速发育期、发育中期；棉花-生育中期）、9月9日（玉米-成熟期；棉花-成熟期）、11月13日（冬小麦-初始生育期、冻融期）的遥感数据。利用Sen2Cor插件对影像数据预处理，并通过ENVI软件反演PDI，利用公式（7）建立通过TDR实测获得的不同生育期32个耕层10 cm土壤样本的实际土壤含水率（体积含水率）和PDI的转换关系，得出土壤含水率模拟值与实测值之间的误差区间为（-0.029～0.032），模型误差较小。经计算得出不同生育期的土壤含水率（图 3），可以看出4月和6月2个生育期的土壤含水率高于其他生育期，8月和11月生育期的土壤含水率较低。

灌区的主要土壤类型为黏土，通过取样测定凋萎含水率为16.6%；田间持水率为32%，通过公式（7）计算得出作物不同生育期土壤水分修正系数（图4）。整体上看，北部滏阳河分区的土壤水分修正系数高于南部的民有分区，中部及东部的土壤水分修正系数偏低。分析其原因，或与灌区地势走向和水源有关，灌区整体呈现北高南低、西高东低的地势及相应的水流走向，因此，地势高靠近水源的区域土壤水分修正系数相对较高。

a. 1月a. Januaryb. 4月b.Aprilc. 6月c.June

d. 8月d. Auguste. 9月e. Septemberf. 11月f. November

2.2 灌区需水量计算结果

根据公式（1）～（3）计算12个月3种主要作物的灌区需水量（表2）。灌区需水量全年共计1.133×109m3，其中，5月和12月的灌区需水量分别为全年最大和最小值，全年占比分别为25.3%和1.2%，4月至8月为作物生长需水高峰期，5个月的累计需水量占全年需水量的比值高达76.8%。

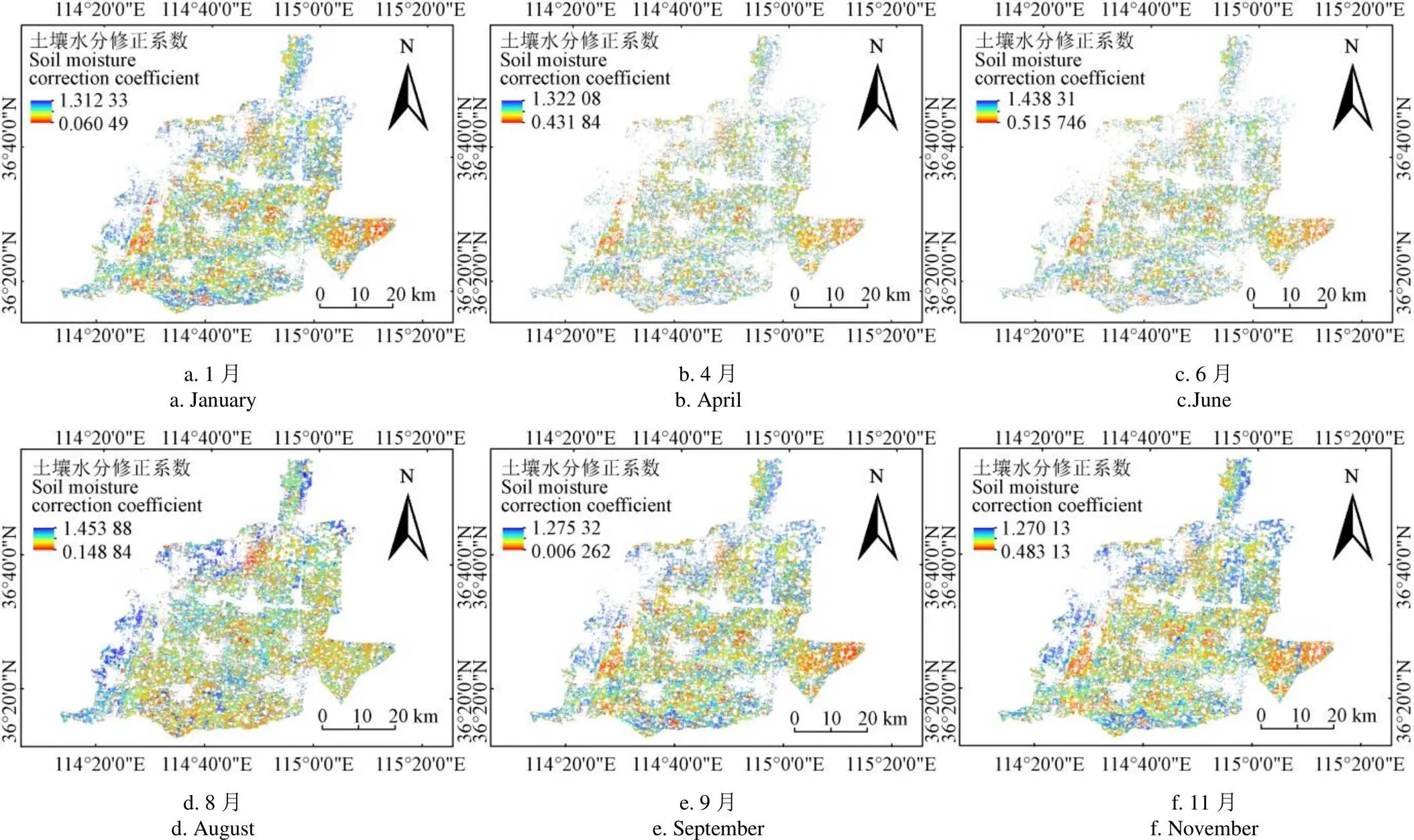
图4 土壤水分修正系数分布图

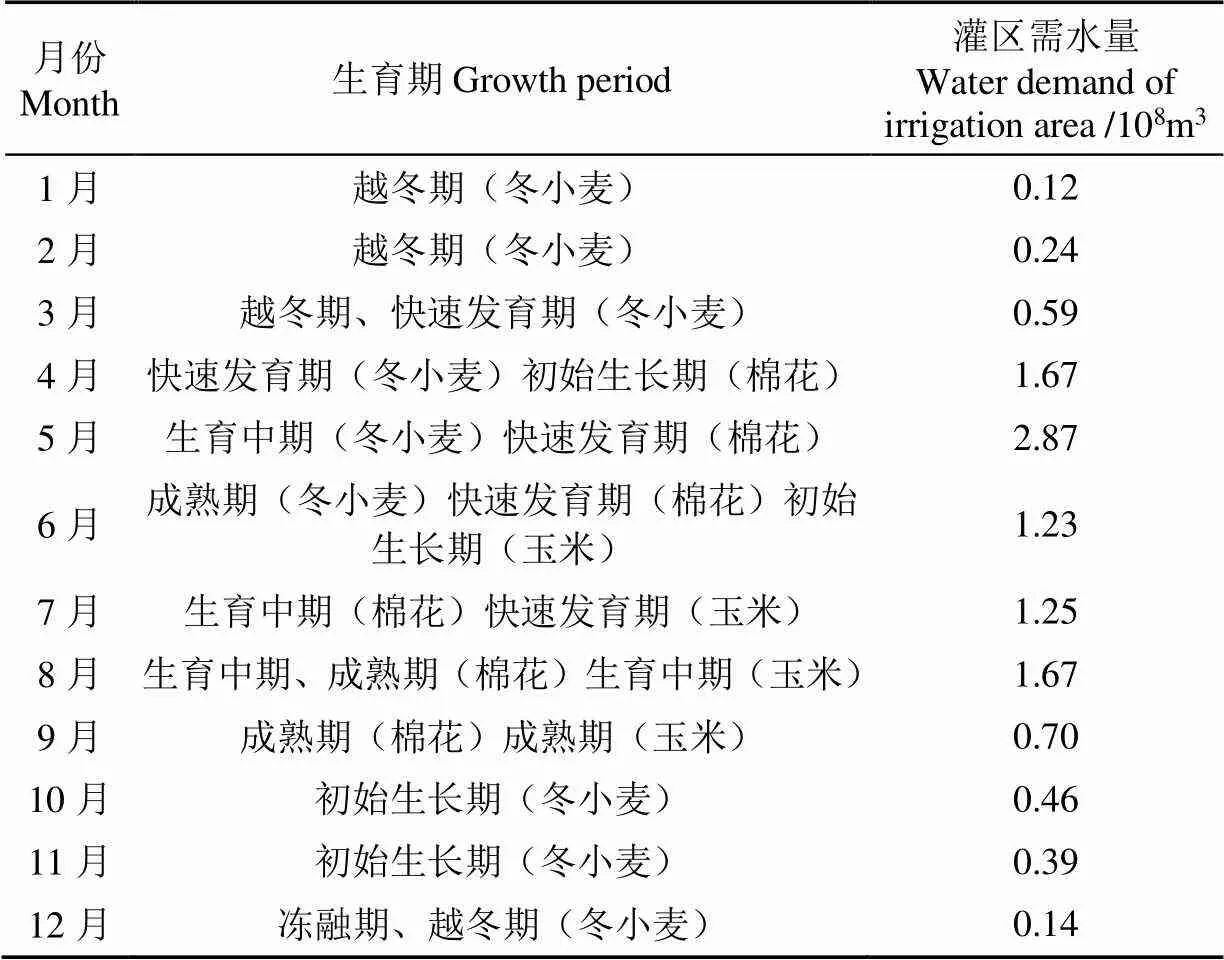
表2 不同生育期灌区需水量统计结果

2.3 优化配置结果分析

将表2、表3中的结果及参数代入一阶段模型中。其中，表3为优化配置模型主要输入参数及变量。1、2、Min1、Max1、Min2、Max2数据源自漳釜河灌区规划设计报告，1、2通过公式（12）计算得出，、P、P1、P2数据源自《邯郸市统计年鉴》。

2.3.1 一阶段模型结果分析

利用Matlab和Lingo11求解建立的漳滏河灌区分布式多水源优化配置模型。图5为不同情景多水源配水量统计图，可以看出首选水源的配水量均高于外调水源，水库配水量配水区间为4.100×108～5.045×108m3;南水北调配水量区间为1.143×108～2.156×108m3，引黄配水量区间为0.982×108～1.486×108m3，引黄配水量略低于南水北调配水量，但南水北调的供水子单元要多于引黄供水子单元，因此，从单位面积配水量角度上看，模型优先选择引黄水作为外调水源。9种情景的灌区总缺水量区间跨度大，其中，VH-PL、VM-PL和VL-PL情景的缺水量明显，VH-PH、VM-PH、VL-PH情景的缺水量几乎为0。随着降水量的增加，不同水源的配水量及灌区总缺水量变化明显，而水库来水流量的变化对配水结果的影响甚微；可见，对于漳釜河灌区而言，降水量较水库来水流量对灌区配水的影响明显，这与该灌区的土壤类型有关[30]。

表3 优化配置模型主要输入参数及变量

图5 不同情景多水源配水量统计图

进一步分析各子单元的空间配水情况。因水库来水流量对配水结果的影响较小且受篇幅限制，此处将9种情景按照丰、平、枯3种来水水平统计不同子单元的总配水量。表4为不同情景配水量的空间统计结果。整体上民有分区的总配水量高于滏阳河分区，这与2.1节中土壤含水率的结果相呼应，对于土壤含水率低的子单元，模型会分配更多水量；随着来水水平增加，滏阳河分区各子单元间的配水量比例相对稳定，而民有分区各子单元的配水量变化明显，特别是M05、M06、M07的配水量变化最明显。对比图3可以看出，靠近北部及西部水源的子单元，其土壤含水率相对较高且变化趋势稳定，模型对该区域分配的水量也相对均衡，而对于东南部的子单元，由于远离水源、土壤含水率低，作物配水过程受水源的影响会更明显。总体而言，模型的配水结果符合实际配水情况。

2.3.2 二阶段模型结果分析

通过1.5.2节中二阶段模型计算出不同情景灌区最大经济效益分别为：265 053.2万元（VH-PH）、271 386.6万元（VH-PM）、264 238.3万元（VH-PL）、265 053.2万元（VM-PH）、271 116.9万元（VM-PM）、276 027.2万元（VM-PL）、264 219.1万元（VL-PH）和270 847.1万元（VL-PM）、276 000.0万元（VL-PL）；灌区收益最大的情景为VH-PM，最小为VL-PH情景。为分析漳滏河灌区经济效益受不同水源的影响程度，将灌区经济效益与总配水量、水库配水量、南水北调配水量、引黄配水量、降水量及总缺水量进行相关分析（表5）。从表5看出灌区经济效益南水北调配水量呈显著负相关。灌区经济效益与供水成本和水价有关，成本及水价越低，灌区经济效益越大[32]，由于南水北调水源的水价相对较高，因此，模型在水库配水不足的情况下，优先选择水价低、单位面积配水量大的引黄水源，以达到灌区经济效益最大的目标，这与2.3.1小节的结论相吻合。此外，总配水量与降水量、引黄配水量，以及水库配水量与引黄配水量、引黄配水量与降水量之间的相关系数均在0.99以上，相关性显著。某水源的配水量增加会导致总配水量的增加；而降水量与各水量呈显著负相关，降水充足的情况下，相应的各子单位的配水量随之减少，可见灌区多水源形成配水系统内部联动紧密[31]。

表5 灌区经济效益与各水量间相关分析

注：**表示在0.01水平上显著；*表示在0.05水平上显著。

Note: ** Indicates significant at 0.01 level; * Indicates significant at 0.05 level.

3 结论与建议

为研究灌区多水源时空配水问题，本文分别以水库配水缺水量最小、灌区经济效益最大为目标建立了分布式多水源时空优化配置模型，并以河北省邯郸市漳滏河灌区为应用实例，分析9种情景下的优化配置结果。主要结论如下：

1）漳滏河灌区4月、6月的土壤含水率高，8月和11月较低；滏阳河分区的土壤含水率高于民友分区；通过遥感技术获取的不同生育期土壤水分修正系数精确度高；灌区年需水量1.133×109m3。

2）外调水源中，南水北调配水量略高于引黄配水量；滏阳河分区各子单元间的配水量比例相对稳定，而民有分区各子单元的配水量变化明显，民有分区的总配水量高于滏阳河分区。

3）灌区收益最大的情景为蓄水高值-降水平值（VH-PM），最小为蓄水低值-降水丰值（VL-PH）情景；外调水源优先选择水价低、单位面积配水量大的引黄水；多水源间的相关性显著，配水系统内部联动紧密。

水资源优化配置模型是应用性较强的系统性模型，本研究构建的灌区分布式多水源时空优化配置模型的创新性体现在：1）考虑了灌区土壤水分参数的空间性，使得各子单元的土壤水分修正系数都能够反映作物和土壤的实际情况。2）厘清了各子单元的供水关系，为实际配水管理工作提供了更具体的理论指导和技术支撑。3）提升了灌区多水源配水管理的决策能力，使灌区综合效益最大化。

灌区水循环过程的不确定性会对配水结果产生影响。因此，在今后的研究中需补充多水源的不确定性分析。由于遥感数据质量和实测土壤样本数量的限制，本研究只得出了全年6个月的土壤水分修正系数，下一步研究会结合不同作物种植结构得出更符合实际情况的土壤水分修正系数。

[1] Li M, Cao X, Liu D, et al. Sustainable management of agricultural water and land resources under changing climate and socio-economic conditions: A multi-dimensional optimization approach[J]. Agricultural Water Management, 2022, 259: 107235.

[2] Li M, Fu Q, Singh V P, et al. Stochastic multi-objective modeling for optimization of water-food-energy nexus of irrigated agriculture[J]. Advances in Water Resources, 2019, 127: 209-224.

[3] 齐学斌，黄仲冬，乔冬梅，等. 灌区水资源合理配置研究进展[J]. 水科学进展，2015, 26(2)：287-295.

Qi Xuebi, Huang Zhongdong, Qiao Dongmei, et al. Research advances on the reasonable water resources allocation in irrigation district[J]. Advances in Water Science, 2015, 26(2): 287-295. (in Chinese with English abstract)

[4] 齐学斌，樊向阳，王景雷，等. 井渠结合灌区水资源高效利用调控模式[J]. 水利学报，2004，35(10)：119-124.

Qi Xuebi, Fan Xiangyang, Wang Jinglei, et al. Optimal allocation of water resources in well-canal combined irrigated area for high efficient utilization of water[J]. Journal of Hydraulic Engineering, 2004, 35(10): 119-124. (in Chinese with English abstract)

[5] 张展羽，高玉芳，李龙昌，等. 沿海缺水灌区水资源优化调配耦合模型[J]. 水利学报，2006，37(10)：1246-1252, 1258.

Zhang Zhanyu, Gao Yufang, Li Longchang, et al. Optimal utilization of water resource in coastal water-deficient irrigation region[J]. Journal of Hydraulic Engineering, 2006, 37(10): 1246-1252, 1258. (in Chinese with English abstract)

[6] 李茉，姜瑶，郭萍，等. 考虑不同层次利益主体的灌溉水资源优化配置[J]. 农业机械学报，2017，48(5)：199-207.

Li Mo, Jiang Yao, Guo Ping, et al. Irrigation water optimal allocation considering stakeholders of different levels[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(5): 199-207. (in Chinese with English abstract)

[7] 姜秋香，付强，朱长虹，等. 基于多维临界调控理论的水资源优化配置研究进展[J]. 东北农业大学学报，2015，46(7)：103-108.

Jiang Qiuxiang, Fu Qiang, Zhu Changhong, et al. Research progress of water resources optimal allocation based on theory of multidimensional critical regulation and control[J]. Journal of Northeast Agricultural University, 2015, 46(7): 103-108. (in Chinese with English abstract)

[8] 李晨洋，张志鑫. 基于区间两阶段模糊随机模型的灌区多水源优化配置[J]. 农业工程学报，2016，32(12)：107-114.

Li Chenyang, Zhang Zhixin. Multi-water conjunctive optimal allocation based on interval-parameter two-stage fuzzy-stochastic programming[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(12): 107-114. (in Chinese with English abstract)

[9] Abdullah A, Ahmed A, Akhter P, et al. Potential for sustainable utilisation of agricultural residues for bioenergy production in Pakistan: An overview[J]. Journal of Cleaner Production. 2021, 287: 125047.

[10] Belmonte B A, Benjamin M F D, Tan, Raymond R T. Systems in the water-energy-food nexus: The emerging role of process systems engineering[J]. Current Opinion in Chemical Engineering. 2017, 18: 32-37.

[11] 何英，唐晓宇，彭亮，等. 南疆丰收灌区水资源多目标优化配置方案优选[J]. 农业工程学报，2021，37(6)：117-126.

He Ying, Tang Xiaoyu, Peng Liang, et al. Optimized selection of the solution for multi-objective optimal allocation of water resources in Fengshou Irrigation Areas of South Xinjiang[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(6): 117-126. (in Chinese with English abstract)

[12] 潘琦，郭萍，张帆，等. 考虑渠道渗漏的黄羊灌区农业水资源多目标优化配置研究[J]. 水资源与水工程学报，2020，31(4)：166-173.

Pan Qi, Guo Ping, Zhang Fan, et al. Study on multi-objective optimal allocation of agricultural water resources in Huangyang Irrigated Area considering canal leakage[J]. Journal of Water Resources and Water Engineering, 2020, 31(4): 166-173. (in Chinese with English abstract)

[13] Li M, Fu Q, Singh V P, et al. Managing agricultural water and land resources with tradeoff between economic, environmental, and social considerations: A multi-objective non-linear optimization model under uncertainty[J]. Agricultural Systems, 2020, 178: 102685.

[14] Wang Y Z, Liu L, Guo S S, et al. A bi-level multi-objective linear fractional programming for water consumption structure optimization based on water shortage risk[J]. Journal of Cleaner Production, 2019, 237: 117829.

[15] 付强，刘银凤，刘东，等. 基于区间多阶段随机规划模型的灌区多水源优化配置[J]. 农业工程学报，2016，32(1)：132-139.

Fu Qiang, Liu Yinfeng, Liu Dong, et al. Optimal allocation of multi-water resources in irrigation area based on interval-parameter multi-stage stochastic programming model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(1): 132-139. (in Chinese with English abstract)

[16] 李茉，曹凯华，付强. 不确定条件下考虑水循环过程的灌区多水源高效配置[J]. 农业工程学报，2021，37(18)：62-73.

Li Mo, Cao Kaihua, Fu Qiang, et al. Efficient allocation of multiple water sources in irrigation areas considering water cycle process under uncertainty[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(18): 62-73. (in Chinese with English abstract)

[17] Brown P D, Cochrane T A, Krom T D. Optimal on-farm irrigation scheduling with a seasonal water limit using simulated annealing[J]. Agricultural Water Management, 2010, 97(6): 892-900.

[18] 彭世彰，王莹，陈芸，等. 灌区灌溉用水时空优化配置方法[J]. 排灌机械工程学报，2013，31(3)：259-264.

Peng Shizhang, Wang Ying, Chen Yun, et al. Method for optimal spatial and temporal allocation of water in irrigation districts[J]. Journal of Drainage and Irrigation Machinery Engineering, 2013, 31(3): 259-264. (in Chinese with English abstract)

[19] 乔长录，刘招，茯苓. 基于COMGIS和Matlab的泾惠渠灌区灌溉决策支持系统[J]. 干旱地区农业研究，2010，28(3)：31-36，70.

Qiao Changlu, Liu Zhao, Fu Ling. lrrigation decision support system based on COMGIS and Matlab for Jinghuiqu irrigation district[J]. Agricultural Research in the Arid Areas, 2010, 28(3): 31-36, 70. (in Chinese with English abstract)

[20] Chen Y, Yu J, Khan S. Spatial sensitivity analysis of multi-criteria weights in GIS-based land suitability evaluation[J]. Environmental Modeling and Software, 2010, 25(12): 1582-1591.

[21] Zaragoza C A, García Irene F, García Isabel M, et al. Spatio-temporal analysis of nitrogen variations in an irrigation distribution network using reclaimed water for irrigating olive trees[J]. Agricultural Water Management, 2022, 262(31): 107353.

[22] Janik G, Kłosowicz I, Walczak A, et al. Application of the TDR technique for the determination of the dynamics of the spatial and temporal distribution of water uptake by plant roots during injection irrigation[J]. Agricultural Water Management, 2021, 252(30): 106911.

[23] Allen R, Pereira L S, Raes D, et al. Crop evapotranspiration: Gudelines for computing crop water requirements-FAO Irrigation and Drainage Paper 56[R]. Rome: Food and Agricultural Organization of the United Nations (FAO), 1998: 56.

[24] Waston K, Rowen L C, Offield T W. Application of thermal modeling in the geologic interpretation of IR images[J]. Remote Sensitive Environment, 1971, 3: 2017-2041.

[25] Price J C. Thermal inertia mapping: A new view of the earth[J]. Journal of Geophysical Research, 1977, 82: 2582-2590

[26] 柯丽娟. 遥感反演土壤含水率在灌溉用水管理中的应用研究[D]. 兰州：兰州交通大学，2015.

Ke Lijuan. Application of Remote SensingInversion of Soil Moisture in the Irrigation Water Management Research[D]. Lanzhou: Lanzhou Jiaotong University, 2015. (in Chinese with English abstract)

[27] Jackson R D, Idso S B, Reginato R J, et al. Canopy temperature as a crop water stress indicator[J]. Water Resource Research, 1981, 17(4): 1133-1138.

[28] Price J C. Using spatial context in satellite data to infer regional scale evapotranspiration[J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28: 940-948.

[29] Feddes R A, Kowalik P, Kolinska K M, et al. Simulation of field water uptake by plants using a soil water dependent root extraction function[J]. Journal of Hydrology, 1976, 31(1/2): 13-26.

[30] 赵敏，郭萍，张妍. 考虑土壤水平衡的灌区水资源优化配置研究[J]. 中国农业大学学报，2020，25(7)：91-102.

Zhao Min, Guo Ping, Zhang Yan. Study on the water potential allocation in irrigation district based on considering soil water balance[J]. Journal of China Agricultural University, 2020, 25(7): 91-102. (in Chinese with English abstract)

[31] 闫旖君，徐建新，陆建红. 人民胜利渠灌区多水源循环转化模型研究[J]. 灌溉排水学报，2017，36(2)：52-57.

Yan Yijun, Xu Jianxin, Lu Jianhong. Research on the multi-water cycle and transformation model in the people’s victory canal irrigation district[J]. Journal of Irrigation and Drainage, 2017, 36(2): 52-57. (in Chinese with English abstract)

Spatial-temporal optimal allocation of distributed multi-water sources in irrigation areas

Liu Wei1,2, Lei Bo1,2※, Liao Jinyi3, Du Lijuan1,2

(1.,,100048,; 2.,,100048,;3.,,232001,)

This research aims to fully consider the spatial and temporal distribution in the process of water supply and demand. A case study was selected as the Zhangfuhe irrigation area, Handan City, Hebei Province, China. The soil moisture and its correction coefficients were also calculated at different growth stages using remote sensing inversion. The demand for each unit was then evaluated in the study area. An optimal allocation model of multi-water sources was established in the irrigation area, particularly with the allocation objectives of the minimum water shortage for the reservoir and the maximum benefit in the irrigation area. The temporal and spatial distribution of water allocation was obtained for the different water sources under nine scenarios, including the high water storage and high precipitation (VH-PH), high water storage and low precipitation (VH-PM), high water storage value and low precipitation value (VH-PL), water storage median and precipitation abundance (VM-PH), water storage median and downgrade value (VM-PM), median impoundment and withered precipitation (VM-PL), low water storage and high precipitation (VL-PH), low water storage and low precipitation (VL-PM), low water storage and low precipitation (VL-PL). The results showed that there was high soil moisture in April and June of the growth period in the irrigation area, and relatively low in August and November. The soil moisture correction coefficient in the Fuyang River district was outstandingly higher than that in the Minyou district. The annual water demand of the irrigation area was 1.133×109m3. Specifically, the water demands in May and December were the maximum and minimum of the whole year, accounting for 25.3% and 1.2%, respectively. The water demand peak of crops was from April to August. Among them, the ratio of cumulative water demand in the five months to the total water demand in the whole year was as high as 76.8 %. The soil moisture correction coefficient using remote sensing inversion was a better agreement with the actual situation. Among the external water sources, the water volume allocated from the south to the north was slightly higher than that of the Yellow River. But, the water volume allocated per unit area of the south to the north water transfer was significantly lower than that of the Yellow River. It infers that the Yellow River was preferentially selected as the external water source in the model. The allocation of water of the Minyou district was higher than that of the Fuyang River district in different scenarios, where the spatial distribution changed outstandingly. The allocation of water in the model better coincided with the practical situation. The economic benefits of the irrigation area were positively related to the precipitation and the total water shortage, while negatively related to the total allocation of water, the allocation of water of the reservoir, the water allocation of the south to the north water, and the allocation water of the Yellow River. Therefore, there was a significant correlation between the water sources, indicating the close internal linkage of the water system. The improved model can provide a new idea for the zoning management of irrigation water, considering the spatial and temporal distribution of multiple water sources and the variation of soil moisture at different growth stages of crops in the irrigation area.

spatial and temporal distribution; soil moisture; precipitation; irrigation area; multiple water sources; agricultural water resources; optimal allocation

10.11975/j.issn.1002-6819.2022.16.015

TV213.4

A

1002-6819(2022)-16-0135-09

刘巍，雷波，廖晋一，等. 灌区分布式多水源时空优化配置 [J]. 农业工程学报，2022，38(16)：135-143.doi：10.11975/j.issn.1002-6819.2022.16.015 http://www.tcsae.org

Liu Wei, Lei Bo, Liao Jinyi, et al. Spatial-temporal optimal allocation of distributed multi-water sources in irrigation areas[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(16): 135-143. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2022.16.015 http://www.tcsae.org

2022-07-06

2022-08-10

国家自然科学基金（52109049），黑龙江省自然科学基金（LH2019E009）

刘巍，博士，高级工程师，研究方向为农业水资源高效利用。Email：liuwei@iwhr.com

雷波，博士，正高级工程师，研究方向为农业水管理。Email：leibo@iwhr.com