喷嘴直径对旋转折射式喷头水量分布特性的影响

高江永，张桐林，侯永胜，李军叶

喷嘴直径对旋转折射式喷头水量分布特性的影响

高江永，张桐林，侯永胜，李军叶

（1. 中国农业机械化科学研究院集团有限公司，北京 100083；2. 土壤植物机器系统技术国家重点实验室，北京 100083）

为了深入理解喷嘴直径对旋转折射式喷头水量分布特性的影响规律，以R3000型旋转折射式喷头为研究对象，配备6槽喷盘，选用36种不同直径（1.79～9.92 mm）的喷嘴，在室内无风环境下，采用雨量筒放射线布置法，开展了98、196和294 kPa 三种工作压力下的旋转折射式喷头水量分布特性试验。试验结果表明：在98 kPa工作压力下，喷嘴直径1.79～7.54 mm喷头的径向水量分布形式为双驼峰型曲线，喷嘴直径7.94～9.92 mm喷头的径向水量分布形式为单驼峰型曲线；在196和294 kPa工作压力下，喷嘴直径1.79～9.92 mm喷嘴的径向水量分布曲线均呈现单驼峰型曲线。旋转折射式喷头的水量分布均匀性随工作压力增加而下降；在98 kPa工作压力条件下，除个别喷嘴直径（1.79、1.98 mm）以外，喷头的水量分布均匀性均在60%以上。喷头的喷洒半径范围为4～9 m。喷头的喷洒半径随喷嘴直径增加并非呈单调递增趋势；当喷嘴直径超过7.54 mm（对应38#喷嘴），随喷嘴直径增加喷洒半径呈下降趋势。根据试验数据分析结果，确定了喷洒半径随喷嘴直径变化的抛物线模型。喷头的喷灌强度最大值和平均值随喷嘴直径增大而增大，曲线拟合结果表明，喷灌强度最大值和平均值均与喷嘴直径呈明显指数关系，决定系数2均在0.95以上。研究结果可为低压旋转折射式喷头优化设计、工程应用及促进产品国产化等提供技术依据和参考。

喷头；喷嘴；喷灌；旋转折射式喷头；喷洒半径；喷灌强度；水量分布

0 引 言

以圆形喷灌机为代表的大型喷灌装备与技术，在农业节水灌溉中发挥着重要作用[1]。低压喷头是大型喷灌装备的关键灌水组件之一。为了满足节水灌溉、变量灌溉和规模化农场发展需求，对低压喷头需求日益增加[2-3]。除了摇臂式喷头实现了国产化以外，圆形喷灌机所使用的低压喷头大多依赖进口，少部分为国内仿制产品[4-5]。目前，国内科研机构已开展多种低压喷头[6-8]研发工作。旋转折射式喷头是一种典型的低压喷头，其工作压力低、喷洒均匀性良好，应用十分广泛。旋转折射式喷头类型与型号多样，目前尚缺乏全面而准确的水量分布技术数据[5]。在喷头配置和计算过程中常采用球体弹道模型[9-10]、曲线拟合[11]等方法对喷头水量分布特性进行模拟和预测。预测精度影响了大型喷灌机组喷头配置和整机喷洒效果。因此，开展旋转折射式喷头水量分布特征试验研究对完善水量分布技术数据、提高喷灌机组水利用率及推动喷头产品国产化进程等均具有重要意义。

喷头的水量分布特性主要包括径向水量分布曲线、喷洒半径、喷灌强度、单喷头均匀性以及组合均匀性等指标。通常，当研究喷头水量分布特性时，需要考虑和考察影响水量分布特性的一些因素。这些因素有：喷头结构形式、喷嘴直径、工作压力、安装高度、风速与风向、液滴分布等。当喷头结构和外部安装条件确定后，喷嘴直径则是影响喷头水量分布特性的关键因素。Kincaid等[12-13]研究了不同结构形式低压折射式喷头的水量分布、液滴直径分布及液滴能量相关特征，每种喷头所采用的喷嘴直径规格为2～6种，比如型号为Nelson Rotator D6的喷头，使用了4种喷嘴直径，分别为4.63、6.16、6.22、9.24 mm。DeBoer等[14]以旋转折射式喷头对象，采用R3000-R4（4槽）、R3000-R6（6槽）、S3000-S6（6槽），配置4种喷嘴直径，分别为4.8, 6.4, 7.9 and 9.9 mm，在50、100、150、200 kPa工作压力下，研究了喷头的水量分布、液滴能量等方面的特性。Faci等[15]研究对比了旋转折射式喷头和固定折射式喷头在安装高度、水量分布均匀性、不同风速等方面的特性，这两种喷头均配置了直径3.8、6.7、7.9 mm 3种喷嘴；研究结果表明，相同条件下，旋转折射喷头的均匀性要高于固定折射喷头；旋转折射喷头使用6.7、7.9 mm喷嘴产生的喷洒区域比固定折射喷头的要宽。国内的学者也开展了相关研究工作。严海军等[16]采用直径2.98、4.96、和6.95 mm的喷嘴，对R3000喷头和A3000喷头的液滴直径特性进行了试验研究。张以升等[10]以D3000喷头为研究对象，采用15#、20#、24#、36#、44#喷嘴，模拟计算了单喷头的喷洒水力特性以及多喷头组合叠加后的喷灌均匀性。朱兴业等[8,17]以自制的R3000喷头为研究对象，配备直径2.98、3.37、3.77 mm的喷嘴，在100、200、300 kPa工作压力下，研究了喷头流量系数、喷洒半径、径向水量分布以及不同安装间距的组合均匀性系数。从上述研究来看，对低压折射式喷头所开展的水量分布特性研究，通常采用5种左右或者更少数量的喷嘴来完成试验和研究任务。目前，关于低压折射式喷头的研究大多如此。又例如Ahmed[18-19]等的研究采用了2种直径的喷嘴，Espinosa[20-22]等的研究采用3种，Sayyadi[23]采用4种，Robles[24]所作的研究涉及6种喷嘴直径。但是，在实际工程应用中，喷嘴是系列产品，喷嘴直径范围较大，与之对应的流量和压力范围也较大。例如，根据Nelson公开的产品信息，3TN系列喷嘴的喷嘴编号从9#至50#，共计42种规格，喷嘴的压力范围为40～340 kPa，全系列喷嘴对应流量范围0.072～7.063 m³/h，但是供应商未公开全部系列喷嘴对应的水量分布曲线。因此，在进行机组喷头配置时，缺乏全系列的水量分布特征，导致无法准确开展机组喷头配置计算和工程应用。另一方面，现有研究采用喷嘴直径规格较少，所得相关成果不足以全面反映喷嘴对水量分布特征的影响规律。

综上所述，为了获得系列喷嘴的喷头水量分布特性，并深入理解喷嘴直径对喷头水量分布特征的影响，为低压旋转喷头设计、应用与国产化等提供技术依据，亟待开展全系列喷嘴的旋转折射式喷头的水量分布试验研究。基于此，本文采用以圆形喷灌机机组常用的低压旋转折射式喷头Nelson R3000喷头为研究对象，选用6槽-12°喷水盘，在98、196、294 kPa 这3种工作压力下，开展配置36种喷嘴直径的喷头径向水量分布特征、喷洒半径以及单喷头均匀性等室内试验，分析研究了喷嘴直径对低压旋转折射式喷头水量分布特征的影响。

1 材料与方法

1.1 材料

试验材料选择Nelson公司的R3000型低压旋转折射式喷头，主要结构为：接头、喷嘴、支架、喷水盘、喷水盘支座、阻尼器。选用的喷水盘为红色喷盘，6槽均布，喷射角为12°，旋转转速1～10 r/min。考虑到国内圆形喷灌机应用的实际情况[5,16]，本文采用喷嘴号为9#～38#，40#、42#、44#、46#、48#、50#，共计36种喷嘴，喷嘴直径范围1.79～9.92 mm（喷嘴直径为编号数与0.198 4 mm的乘积）。所使用旋转折射式喷头结构、喷水盘以及喷嘴实物如图1所示，喷嘴直径详见表1。

1.2 试验装置

本文所有试验在土壤植物机器系统技术国家重点实验室进行。试验装置由水池、潜水电泵、电动阀门、电磁流量计，压力传感器、过滤器、雨量筒等组成。试验设备和测量仪器的规格参数和精度详见文献[25]。雨量筒的布置采用放射线布置法[26]，将雨量筒布置在一条由喷头所在位置引出的放射线上；首个雨量筒中心距喷头0.5 m，后续雨量筒中心间距0.5 m，共计26个。试验装置简图如图2所示。试验过程中，流量、压力、时间、雨量筒水量等相关数据进行自动采集，并通过计算获得喷灌强度以及喷洒半径等水量分布数据。所使用的采集和处理软件为中国农机院开发的喷头测试软件SWCAT系统。试验结束后，SWCAT系统将原始数据、水量分布计算数据等生成excel格式文件。

1.接头 2.喷嘴 3.支架 4.喷水盘 5.喷水盘支座 6.阻尼器

表1 试验条件

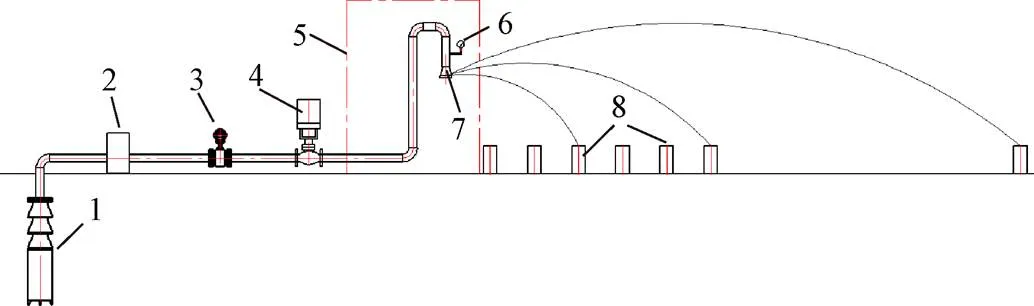
1.潜水电泵 2.过滤器 3.电磁流量计 4.电动阀门 5.挡雨罩 6.压力传感器 7.喷头 8.雨量筒

1.3 试验条件

低压旋转折射式喷头的水量分布试验，需要确定喷头安装高度、工作压力、流量、喷洒时间等关键试验条件。本文试验在室内无风条件下完成。喷头安装高度为1.0 m。工作压力采用喷头常用试验压力98 kPa（10 m）、196 kPa（20 m）、294 kPa（30 m）。在试验过程中，通过调整电动阀门开度，来调整喷嘴的工作压力，达到工作压力后，开始试验，并记录流量。试验喷洒持续时间为30 min。喷嘴编号、喷嘴直径、喷头工作压力、试验流量等试验条件见表1所示。

1.4 试验方法

1.4.1 喷洒半径

使用喷头进行灌溉作业，喷头水射流破碎雾化，形成圆形湿润区域。该湿润区域的半径，称为喷头的湿润半径。喷洒半径是喷头在正常工作条件下，喷头中心线距测出的灌水强度为某一数值的最远点距离[26]，也称为喷头的射程。本文试验中喷洒半径所对应的灌水强度值为0.25 mm/h[27]。

喷头喷洒半径是灌溉喷头的主要性能指标，Kincaid[12]、蔡振华[28]、Liu等[17]在试验结果基础上获得了相应的低压旋转折射式喷头喷洒半径预测模型，张以升等[10]则提出了基于D3000固定折射式喷头的喷洒半径预测模型。预测模型如式（1）～（4）。

Kincaid公式[12]：

蔡振华公式[28]：

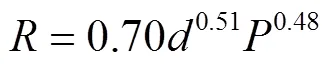
Liu公式[17]：

张以升公式[10]（固定式折射喷头）

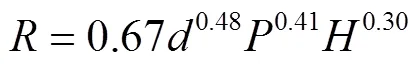
式中为喷洒半径，m；为喷嘴直径，mm；为喷头安装高度，m；为喷头工作压力，m；为喷头流量，L/s。

1.4.2 喷灌强度与径向水量分布

喷灌强度是灌溉区域内某一位置，在单位时间内的平均灌水深度。径向水量分布是评价喷头喷洒性能与指导工程应用的重要特征指标。依据距离喷头的径向距离远近，将距离喷头不同位置的喷灌强度绘制在一起，形成喷头径向水量分布图[26]。

本文中，假设喷头喷洒试验的时间为。在时间内，雨量筒收集到的水量质量为，那么在该位置的单位时间的水深即喷灌强度为

式中WAR为喷灌强度，mm/h；为雨量筒收集的水的总量，kg；为水密度，kg/m³；d为雨量筒开口直径，m，本试验中雨量筒开口直径d为0.15 m。

1.4.3 水量分布均匀性

在标准GB/T 27612.3-2011[26]中，给出了4个评价指标，分别为：克里斯琴森均匀系数（UCC）、统计均匀系数（UCS）、水量分布均匀性（DU）、时序系数（SC）。考虑到本试验特点，本文采用前2个指标评价单喷头的水量分布特性，计算方法[26]如下。

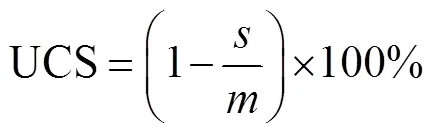
式中为平均值，mm/h；为标准差，mm/h；为平均绝对偏差，等于各个绝对偏差的平均值，mm/h；、、分别为

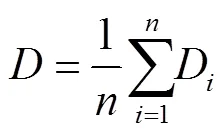
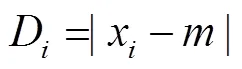
式中为用于分析均匀性的网格数；x为用于分析均匀性的网格中的一个数值，mm/h；D为单个绝对偏差，等于x与之差的绝对偏差值，mm/h。

UCC与UCS二者的关系式[26]为

2 结果与分析

2.1 径向水量分布

在本文中，通过试验获取了量雨筒采集的雨量数据，并采用曲线拟合，得到了不同工作压力下使用36种喷嘴的喷头径向水量分布曲线。在此仅列出直径为1.79、2.38、2.78、3.97、4.76、5.95、7.14、7.94、9.13、9.92 mm喷嘴在不同压力下的喷头径向水量分布曲线，如图3所示。

a. 1.79 mmb. 2.38 mm

c. 2.78 mmd. 3.97 mme. 4.76 mmf. 5.95 mm

从图3不同直径喷嘴的径向水量分布图可知，对于同一喷嘴来说，随着工作压力的增加，喷头湿润半径随之增加；由于随着工作压力增加，喷灌的流量亦随之增加，也导致相同径向位置的喷灌强度随之增加。对于同一喷嘴来说，随着喷头工作压力的增加，喷灌强度最大值的增幅超过150%，产生最大增幅的喷嘴直径为2.78 mm（14#喷嘴）。在相同的工作压力下，喷灌强度最大值随喷嘴直径增加呈递增趋势。在98 kPa工作压力下，直径1.79 mm喷嘴的喷灌强度最大值为5.0 mm/h，喷灌强度平均值为1.79 mm/h；直径9.92 mm喷嘴的喷灌强度最大值为69.6 mm/h，喷灌强度平均值为33.91 mm/h。在196、294 kPa工作压力下，直径1.79 mm喷嘴的喷灌强度最大值分别为4.80、7.36 mm/h，喷灌强度平均值分别为2.31、3.61 mm/h；直径9.92 mm喷嘴的喷灌强度最大值分别为70.64、83.16 mm/h，喷灌强度平均值为38.69、44.56 mm/h。

在98 kPa工作压力下，喷嘴直径小于7.54 mm（对应38#喷嘴）时，喷头的径向水量分布形式呈双驼峰曲线，径向分布曲线存在2个峰值点，两个峰值喷灌强度基本相当，靠近喷头安装的峰值点位于距喷头安装位置约1/4～1/2的湿润半径之间，另一个峰值点位置位于3/4湿润半径处，波谷位置则位于约1/2湿润半径处。当喷嘴直径超过7.94 mm（40#喷嘴），第二峰值基本消失，所形成径向水量分布形式与196、294 kPa压力条件下的水量分布形式一致。在196、294 kPa工作压力下，径向水量分布形状呈现单驼峰形状；最大喷灌强度位置位于距喷头安装位置约1/4～1/2湿润半径之间。在196、294 kPa工作压力下，配置不同喷嘴直径喷嘴，所形成径向水量分布曲线的最大值位置基本一致，该位置与98 kPa工作压力下的第一波峰位置基本相同，距喷头的距离在1.3～3.5 m区间内。R3000旋转折射式喷头的水量分布呈近似三角形分布（单驼峰曲线）或者三角形组合分布（双驼峰曲线）。为了提升喷头喷洒性能，如何通过喷嘴与喷水盘结构设计获得扁平化或者多峰化的水量分布，可作为旋转折射式喷头国产化的关键设计目标之一。

喷灌强度最大值和平均值是喷头水量分布特征的关键信息。为了深入分析喷嘴直径对水量分布的影响规律，进一步对本试验所获得的不同压力和喷嘴的喷灌强度试验数据进行分析，得到不同工作压力下的喷嘴直径与喷灌强度最大值及喷灌强度平均值的关系，如图4所示。

从图4可以发现，在不同工作压力下，随着喷嘴直径增加，对应的喷灌强度最大值和平均值均也增加。这也是随着喷嘴直径的增加，流量增加后产生的必然结果。通过数据曲线拟合，获得了不同工作压力下R3000喷头水量分布图的喷灌强度最大值、平均值与喷嘴直径的指数关系式，即

拟合结果表明：在不同工作压力下，喷灌强度最大值和平均值的拟合决定系数2均大于0.95，表明指数函数关系的拟合精度较高。此外，喷灌强度最大值的拟合决定系数值整体高于均值的拟合决定系数。

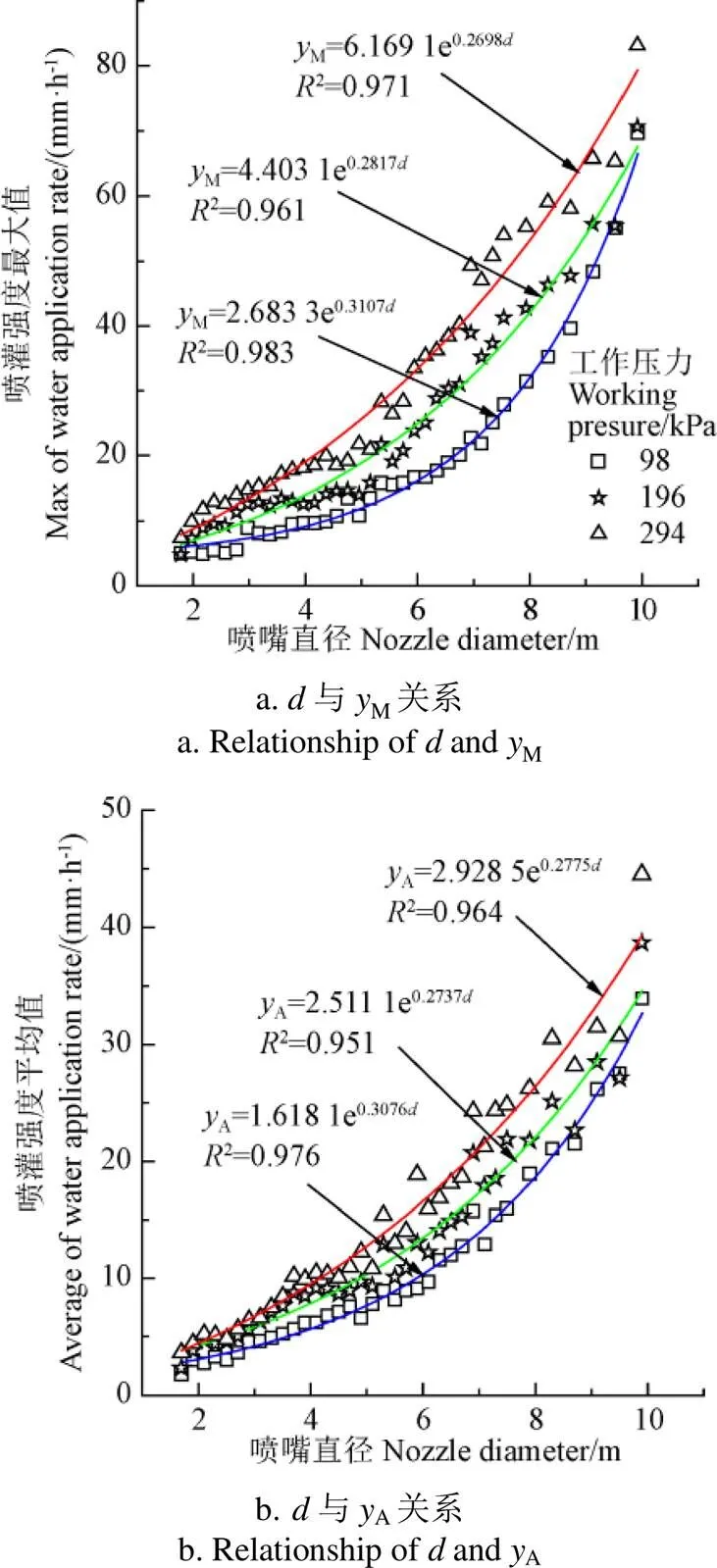
图4 喷嘴直径d与喷灌强度最大值yM及平均值yA的关系

为了进一步核实低压折射喷头的喷嘴直径与喷灌强度最大值以及平均值之间的指数关系是否具有一般性，对文献[29]中公开的Nelson D3000喷头相关实验数据进行分析。该研究以D3000为研究对象，采用固定式36齿喷水盘，在20 PSI （137 kPa）压力下，使用直径1.79～6.55 mm系列喷嘴，对应喷嘴号为9#～33#，该文献公开了不同直径喷嘴对应的喷灌强度最大值和平均值数据。通过对数据处理发现，喷嘴直径与喷灌强度最大值以及平均值之间的也存在近似指数关系，拟合关系式为

喷灌强度最大值M：

喷灌强度平均值A：

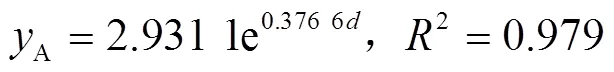
根据本文与文献[29]的数据处理结果，初步判定，对于低压折射式喷头，不论为固定喷水盘还是旋转喷水盘，喷嘴直径与喷灌强度最大值和平均值之间均存在一定的指数关系。在实际应用当中，工程技术人员可以根据选用喷嘴号，利用本文给出的指数关系模型及相关喷洒半径预测模型，估算喷灌强度最大值和喷洒半径，获得喷头的简化三角形的水量分布特征，继而进行喷头配置、机组组合水量分布均匀性的预测和估算。但是该指数关系是否具有普遍性，还需对其他结构形式喷水盘进一步开展试验验证。

2.2 喷洒半径

根据式（1）～（4）可获得对应喷嘴直径的喷洒半径预测值。本文试验喷洒半径及预测值与喷嘴直径关系如图5所示。

a. 98 kPab. 196 kPac. 294 kPa

试验结果表明，采用6槽、12°喷射角度喷水盘的R3000喷头，在98、196、294 kPa工作压力条件下，喷洒半径分别为4～7 m、5.5～9 m、5～9 m。相同工作压力下，喷嘴直径在1.79～7.54 mm范围内，随着喷嘴直径增大，喷洒半径逐渐增大；在喷嘴直径7.94～9.92 mm范围内，随着喷嘴的直径增大，喷洒半径呈下降趋势或略有下降后平稳趋势。本文试验结果显示，下降幅度在0.5～1 m之间。上述喷洒半径的变化趋势，与文献[14]中试验结果一致。在喷嘴直径增大到一定程度后，喷头的喷洒半径出现下降趋势的原因为：对于折射式喷头，需要在合适的工作压力下，才能获得良好的液滴分布和最大喷洒半径[30]。当压力过大，则造成喷溅、折射后，液滴反而变小，不能实现最大的喷洒半径；压力过小，则对于液滴破碎不利，造成液滴过大，射流范围小。所以旋转折射式喷头在实现国产化过程中，如何控制射流液滴破碎是设计和科研人员需要深入研究方向之一。

根据图5可知，与试验数值对比，式（4）预测喷洒半径值整体较低；说明在同等安装条件下，旋转折射式喷头比固定折射式喷头的喷洒半径要大，此结果与文献[15]等研究成果吻合；因此，固定折射式喷头的预测公式不适用于旋转折射式喷头的喷洒半径预测，后续不予讨论。从整体趋势上，式（1）～（3）这3个经验预测模型获得的喷洒半径预测值随喷嘴直径增加而增加，喷洒半径整体趋势递增并无中间拐点；而本文试验中，直径1.79～7.54 mm喷嘴的喷洒半径值与经验公式预测值整体趋势基本相同，喷洒半径随喷嘴直径增大而增加；以直径7.54 mm（对应38#喷嘴）为分界点，喷洒半径呈略微下降趋势。上述结果表明，3个预测模型不能有效预测旋转折射式喷头喷洒半径随喷嘴直径变化趋势，3个预测模型相对误差值如表2所示。

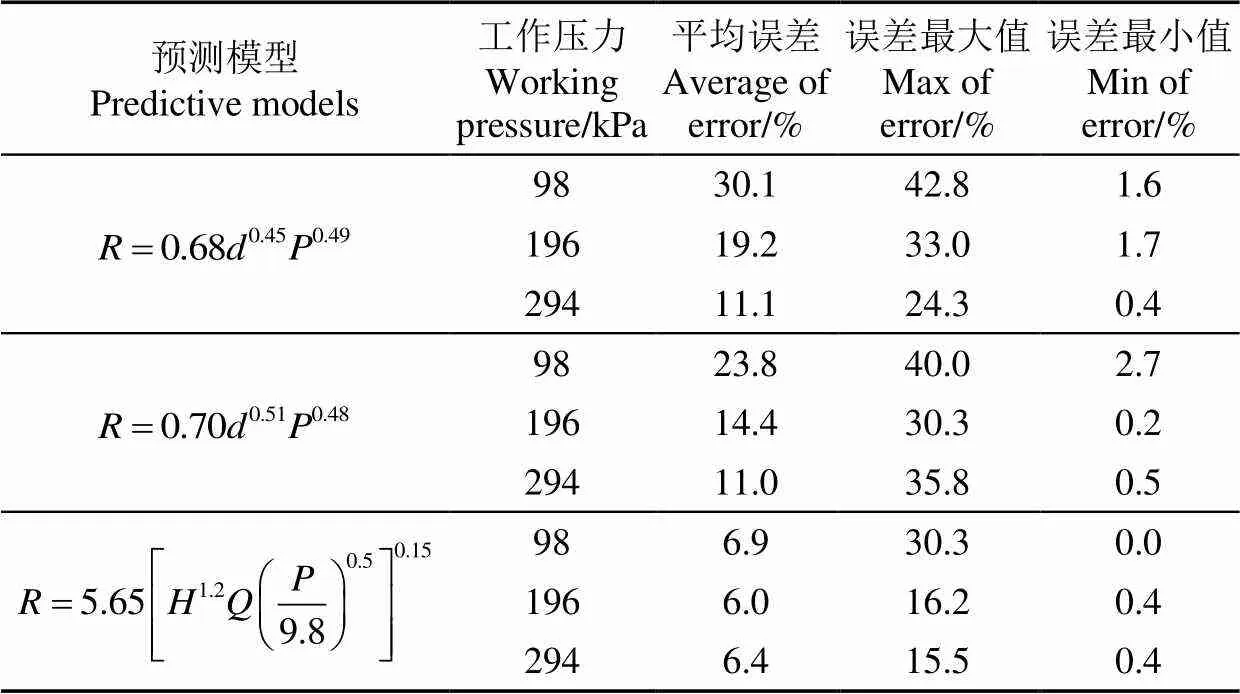
表2 喷洒半径经验公式预测值与实测值相对误差

注：为喷头安装高度，m；为喷头工作压力，m；为喷头流量，L/s。

Note:is height of sprinkler, m；is working pressure of sprinkler, m;is flow rate of sprinkler, L/s.

从图5及表2可以发现，整体上，对于直径1.79～7.54 mm喷嘴，公式（1）的预测精度较高，误差最大值为30.3%，平均误差最大值为6.9%。对于直径超过7.54 mm的喷嘴，3个经验公式对喷洒半径的预测精度和整体趋势均不能正确反映试验结果及趋势。

将喷洒半径试验结果数据进行数据拟合，可获得不同压力条件下，喷嘴直径与喷洒半径之间的关系，呈抛物线分布，采用二次多项式拟合，决定系数均为0.8以上，说明拟合精度较高，拟合关系式可很好反映二者关系。

对于低压旋转折射式喷头，研究试验常采用的安装高度有1.0、1.2、1.5、2.0、2.5 m。该类型喷头的喷洒半径范围为5～10 m。在相同压力和喷嘴的条件下，随着安装高度的变化（1.0～2.5 m范围内），喷洒半径的变化量基本在0.5～1.5 m范围内[18,21,31]。因此，对于图5中的喷洒半径与喷嘴直径相互关系的拟合公式，虽然在安装高度1.0 m条件下获得，但是可以将其作为其他常用安装高度（1.0～2.5 m）喷头研究的技术或工程应用依据。

2.3 水量分布均匀性

将不同压力下系列喷嘴的喷灌试验数据采用式（6）～（11）对均匀性系数进行计算，获得喷嘴直径与UCC之间的变化关系，如图6所示。

单喷头均匀性系数的计算结果表明，喷头的克里斯琴森均匀系数UCC范围为25%～75%。在98 kPa工作压力下，除了直径1.79、1.98 mm的喷嘴外，其余喷嘴的均匀性系数UCC在60%～75%之间。在196 kPa工作压力下，则是只有直径2.98、3.57 mm喷嘴的均匀性系数UCC低于40%，其余在40%～75%之间。在294 kPa工作压力下，直径小于3.57 mm的喷嘴，UCC范围为25%～40%，直径大于3.57 mm的喷嘴，UCC范围为40%～67%。由于压力的提高，在距离喷头安装位置比较近的区域获得的小尺度的液滴增多，所以造成喷头整体均匀性下降，特别是喷嘴直径较小的条件下，雾化更为严重，以上分析待进一步的液滴实测试验进行验证。总体而言，对于同一喷嘴，294 kPa工作压力的均匀性要低于196 kPa工作压力下的均匀性，98 kPa工作压力的均匀性系数最高。

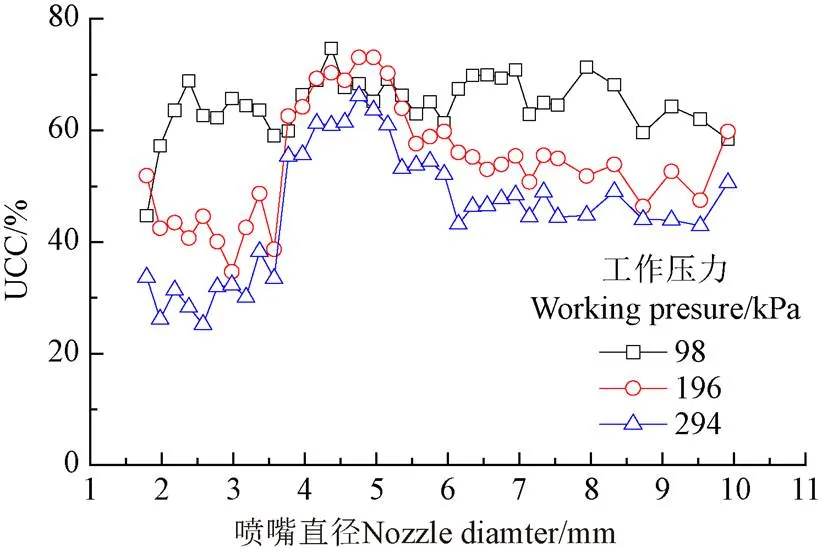
图6 不同喷嘴的单喷头克里斯琴森均匀系数

单喷头的均匀性系数对于喷头设计与制造的国产化，提供了参考和依据。UCC和UCS的对应关系及拟合的直线，如图7所示。

图7 UCC与统计均匀系数（UCS）的关系

从图7结果可知，UCC和UCS存在线性关系，但与GB/T 27612.3—2011推荐公式（式（12））有所差异。因此，在旋转折射式喷头设计和国产化过程中，可采用图7中拟合关系式替代GB/T 27612.3—2011推荐关系式来衡量或确定喷头产品水量分布均匀性。

3 结 论

本文以R3000型旋转折射式喷头为研究对象，配备6槽-12°红色喷盘，喷头安装高度1 m，在98 、196和294 kPa 3种工作压力下，采用36种喷嘴直径，开展了喷头水量分布特性试验，分析和研究了喷嘴直径对喷头水量分布特征的影响，得到如下结论：

1）在3种工作压力和1 m安装高度条件下，使用全系列喷嘴的喷头喷洒性能参数为：喷洒半径为4～9 m，喷灌强度最大值范围为4.80～83.16 mm/h，喷灌强度平均值范围为1.79 ～44.56 mm/h，单喷头的克里斯琴森均匀系数UCC范围为25%～75%。

2）R3000喷头的喷洒半径随喷嘴直径增加并非呈单调递增趋势，当喷嘴直径超过7.54 mm（对应38#喷嘴）后，随喷嘴直径增加喷洒半径呈下降趋势；通过对实测数据的数据进行拟合，拟合结果表明在一定工作压力下喷洒半径与喷嘴直径呈近似抛物线关系。

3）对于R3000旋转折射喷头，在3种工作压力下，喷灌强度最大值和平均值随喷嘴直径增大而增大；喷灌强度最大值和平均值均与喷嘴直径呈明显指数关系，拟合决定系数2均在0.95以上。初步判断，低压折射式喷头的喷灌强度最大值和平均值与喷嘴直径的存在指数关系。

[1] 刘俊萍，朱兴业，袁寿其，等. 中国农业节水喷微灌装备研究进展及发展趋势[J]. 排灌机械工程学报，2022，40(1)：87-96.

Liu Junping, Zhu Xingye, Yuan Shouqi, et al. Research and development trend of agricultural water-saving sprinkler and micro-irrigation equipment in China[J]. Journal of Drainage and Irrigation Machinery Engineering, 2022, 40(1):87-96. (in Chinese with English abstract)

[2] 李仰斌，刘俊萍. 中国节水灌溉装备与技术发展展望[J]. 排灌机械工程学报，2020，38(7)：738-742.

Li Yangbin, Liu Junping. Prospects for development of water-saving irrigation equipment and technology in China[J]. Journal of Drainage and Irrigation Machinery Engineering, 2020, 38(7): 738-742. (in Chinese with English abstract)

[3] 赵伟霞，李久生，栗岩峰. 大型喷灌机变量灌溉技术研究进展[J]. 农业工程学报，2016，32(13)：1-7.

Zhao Weixia, Li Jiusheng, Li Yanfeng. Review on variable rate irrigation with continuously moving sprinkler machines[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(13):1-7. (in Chinese with English abstract)

[4] Yan H, Hui X, Li M, et al. Development in sprinkler irrigation technology in China[J]. Irrigation and Drainage, 2020, 69: 75-87.

[5] 侯永胜，董晓丽，严海军，等. 圆形喷灌机喷头选型及配置[J]. 农业工程，2021，11(10)：9-19.

Hou Yongsheng, Dong Xiaoli, Yan Haijun, et al. Nozzle select and configuration of center pivot sprinkler[J]. Agricultural Engineering, 2021, 11(10): 9-19. (in Chinese with English abstract)

[6] 刘俊萍，李红，张前，等. 旋转式喷头空间流道设计及低压水力性能试验[J]. 农业工程学报，2022，38(5)：65-71.

Liu Junping, Li Hong, Zhang Qian, et al. Space flow channel design of rotary sprinkler and hydraulic performance experiments at low pressure[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(5): 65-71. (in Chinese with English abstract)

[7] Chen R, Li H, Wang J, et al. Effects of pressure and nozzle size on the spray characteristics of low-pressure rotating sprinklers[J]. Water, 2020, 12(10): 2904.

[8] 朱兴业，万景红，Alexander Fordjour，等. 旋转折射式喷头水量分布与喷灌均匀性试验[J]. 农业机械学报，2018，49(8)：145-152.

Zhu Xingye, Wan Jinghong, Alexander Fordjour, et al. Experiment of water distribution and uniformity of rotating plate sprinkler[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(8): 145-152. (in Chinese with English abstract)

[9] Robles O, Latorre B, Zapata N, et al. Self-calibrated ballistic model for sprinkler irrigation with a field experiments data base[J]. Agricultural Water Management, 2019, 223(12): 105711.

[10] 张以升，朱德兰，张林，等. 基于弹道轨迹方程的折射式喷头水量分布计算模型[J]. 农业机械学报，2015，46(12)：55-61.

Zhang Yisheng, Zhu Delan, Zhang Lin, et al. Water distribution model of fixed spray slate sprinkler based on ballistic trajectory equation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(12): 55-61. (in Chinese with English abstract)

[11] Zhang Y, Guo J, Sun B, et al. Modeling and dynamic-simulating the water distribution of a fixed spray-plate sprinkler on a lateral-move sprinkler irrigation system[J]. Water, 2019, 11(11): 2296.

[12] Kincaid D C. Application rates from center pivot irrigation with current sprinkler types[J]. Applied Engineering in Agriculture, 2005, 21(4): 605-610.

[13] Kincaid D C, Solomon K H, Oliphant J C. Drop size distributions for irrigation sprinklers[J]. Transactions of the ASAE, 1996, 39(3): 839-845.

[14] DeBoer D W. Drop and energy characteristics of a rotating spray-plate sprinkler[J]. Journal of Irrigation and Drainage Engineering, 2002, 128(3): 137-146.

[15] Faci J M, Salvador R, Playán E, et al. Comparison of fixed and rotating spray plate sprinklers[J]. Journal of Irrigation and Drainage Engineering, 2001, 127(4): 224-233.

[16] 严海军，肖建伟，李文颖，等. 圆形喷灌机低压阻尼喷头水滴直径分布规律的试验研究[J]. 水利学报，2014，45(4)：467-473.

Yan Haijun, Xiao Jianwei, Li Wenying, et al. Droplet size distributions of low-pressure damping sprinklers used in center-pivot irrigation systems[J]. Journal of Hydraulic Engineering, 2014, 45(4): 467-473. (in Chinese with English abstract)

[17] Liu J, Zhu X, Yuan S, et al. Hydraulic performance assessment of sprinkler irrigation with rotating spray plate sprinklers in indoor experiments[J]. Journal of Irrigation and Drainage Engineering, 2018, 144(8): 06018005.

[18] Ahmed M A M, Awaad M A, El-Ansary M Y, et al. Performance of rotating spray plate sprinklers[J]. Misr Journal of Agricultural Engineering, 2010, 27(2): 565-585.

[19] Al-agele H A, Mahapatra D M, Prestwich C, et al. Dynamic adjustment of center pivot nozzle height: an evaluation of center pivot water application pattern and the coefficient of uniformity[J]. Applied Engineering in Agriculture, 2020, 36(5): 647-656.

[20] Espinosa E R J, González M D. Caracterización del emisor Rotatortm r3000 en condiciones aisladas[J]. Revista Ciencias Técnicas Agropecuarias, 2009, 18(2): 53-56.

[21] Sourell H, Faci J M, Playán E. Performance of rotating spray plate sprinklers in indoor experiments[J]. Journal of Irrigation and Drainage Engineering, 2003, 129(5): 376-380.

[22] Friso D, Bortolini L. Influence of the trajectory angle and nozzle height from the ground on water distribution radial curve of a sprinkler[J]. Journal of Agricultural Engineering, 2012, 43(1): 16-25.

[23] Sayyadi H, Nazemi A H, Sadraddini A A, et al. Characterising droplets and precipitation profiles of a fixed spray-plate sprinkler[J]. Biosystems Engineering, 2014, 119: 13-24.

[24] Robles Rovelo C O, Zapata Ruiz N, Burguete Tolosa J, et al. Characterization and simulation of a low-pressure rotator spray plate sprinkler used in center pivot irrigation systems[J]. Water, 2019, 11(8): 1684.

[25] 高江永，侯永胜，李卫星，等. 圆形喷灌机低压阻尼喷头水力性能试验[J]. 农业工程，2016，6(4)：54-58.

Gao Jiangyong, Hou Yongsheng, Li Weixing, et al. Hydraulic Performance Test of Low Pressure Damping Nozzle for Circular Sprinkler[J]. Agricultural Engineering, 2016, 6(4): 54-58. (in Chinese with English abstract)

[26] 中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会. 农业灌溉设备喷头第3部分：水量分布特性和试验方法，GB/T 27612. 3- 2011 [S]. 北京：中国标准出版社，2011.

[27] 中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会. 农业灌溉设备旋转式喷头第1部分：结构和运行要求，GB/T 19795. 1- 2005 [S]. 北京：中国标准出版社，2005.

[28] 蔡振华. 中心支轴式喷灌机关键灌水组件开发及试验研究[D]. 北京：中国农业机械化科学研究院，2009.

Cai Zhenhua. Development of Center Pivot Irrigation System Sprinkler Package and Experimental Study on Low Pressure Spray-head[D]. Beijing: Chinese Academy of Agricultural Mechanization Sciences, 2009. (in Chinese with English abstract)

[29] Yan H J, Jin H Z, Qian Y C. Characterizing center pivot irrigation with fixed spray plate sprinklers[J]. Science China Technological Sciences, 2010, 53(5): 1398-1405.

[30] Kranz B, Yonts C D, Martin D L. Operating characteristics of center pivot sprinklers[M]. Cooperative Extension, University of Nebraska-Lincoln, 2005.

[31] 张以升，朱德兰，宋博，等. 基于弹道理论有风条件下折射式喷头喷灌均匀度研究[J]. 农业机械学报，2017，48(2)：91-97，81.

Zhang Yisheng, Zhu Delan, Song Bo, et al. Uniformity of fixed spray plate Sprinkler under windy condition based on ballistic simulation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(2): 91-97, 81. (in Chinese with English abstract)

Effects of nozzle diameter on water distribution for rotating spray-plate sprinkler

Gao Jiangyong, Zhang Tonglin, Hou Yongsheng, Li Junye

(1..,.,100083,; 2.--,100083,)

This study aims to deeply understand the influence of nozzle diameter on the water distribution characteristics of rotating spray plate sprinklers. The experiment was carried out in a windless indoor environment. An R3000 rotating spray plate sprinkler was selected as the research object with the 6-groove red spray plate and 36 nozzles (diameter 1.79-9.92 mm). The water distribution characteristics of rotating spray plate sprinkler under three working pressures of 98, 196, and 294 kPa were tested using radial collector arrays method. The results show that the radial water distribution patterns of 9#-38# nozzle (diameter 1.79-7.54 mm) presented a double hump curve under 98 kPa working pressure condition, while the patterns of 40#-50# nozzle (diameter 7.94-9.92 mm) was a single hump curve. The radial water distribution patterns of all nozzles showed a single hump curve under the working pressure of 196 and 294 kPa. The maximum was all the same as the radial position in the radial water distribution curves with the different diameter nozzles, which was basically the same as the first peak position under the working pressure of 98 kPa. The position was usually between 1.3 and 3.5 m away from the nozzle. The maximum and average values of water application rate increased with the increase of nozzle diameter. It was found that the maximum water application rate presented an exponential relationship with the nozzle diameter using curve fitting. An exponential relationship was found in the average value of water application rate with the nozzle diameter. The coefficients of determination (2) of the fitting formulas were above 0.95. There was exponentially related to the maximum and average value of water application rate and the nozzle diameter. However, the universal index relationship was further verified by the other structural forms of spray-plate. The spray radius was 4-7 m when the working pressure was 98 kPa. The spray radius was 5.5-9 m when the working pressure was 196 kPa. When the working pressure was 294 kPa, the spray radius was 5-9 m. There was no monotonic increase in the spray radius with the increase of nozzle diameter, while the nozzle diameter exceeded 7.54 mm (38# nozzle). The test showed that a parabolic model was established to determine the variation of the spray radius with the nozzle diameter under pressure. Three prediction models only applied to the rotating spray-plate sprinkler with a nozzle diameter of less than 7.54 mm. The prediction error was large after exceeding the diameter. There was a uniform decrease in the water distribution for the rotating spray plate sprinkler with the increase in working pressure. The water distribution uniformity of the single nozzle was more than 60%, under the pressure condition of 98 kPa, except for the 9# and 10# nozzle (diameter 1.79 and 1.98 mm). The water distribution of the R3000 rotating spray-plate sprinkler was approximately triangular (single hump curve) or a triangular combination distribution (double hump curve). The flow rate of nozzle was determined by the working pressure and nozzle diameter. The uniformity, the characteristics of the water distribution and the spraying radius depended on the structure and speed of the spray plate. Therefore, flat or multi-peak water distribution was the key goal to design the spray-plate structure in the rotating spray plate sprinkler for better spraying performance. The finding can provide the technical basis and reference for the optimization design, engineering application and product localization of low-pressure rotating spray plate sprinklers.

sprinkler; nozzle; sprinkler irrigation; rotating spray-plate sprinkler; wetted radius; water application rate; water distribution

10.11975/j.issn.1002-6819.2022.16.010

S275.5

A

1002-6819(2022)-16-0090-08

高江永，张桐林，侯永胜，等. 喷嘴直径对旋转折射式喷头水量分布特性的影响[J]. 农业工程学报，2022，38(16)：90-97.doi：10.11975/j.issn.1002-6819.2022.16.010 http://www.tcsae.org

Gao Jiangyong, Zhang Tonglin, Hou Yongsheng, et al. Effects of nozzle diameter on water distribution for rotating spray-plate sprinkler[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(16): 90-97. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2022.16.010 http://www.tcsae.org

2022-06-23

2022-08-06

河北省重点研发计划（20327205D）；国家重点研发计划(2017YFD0201502)

高江永，博士，高级工程师，研究方向为水力机械与水动力学、节水灌溉技术等。Email：gao_jiangyong@163.com