多机器人协同制造系统时序约束任务调度优化方法
刘少睿,田 威,沈建新,李 波,胡俊山
(南京航空航天大学 机电学院,江苏 南京 210016)
0 引言
诸如飞机机身、飞船舱体等大型复杂结构的制造任务是航空航天领域中一类典型难题,其工作量大、周期长、精度要求高,且直接影响最终产品的成本和服役性能。当前,新一代产品正呈现大型化和复杂化的趋势,结构件尺寸普遍超过现有加工中心的工作行程,导致近年来多机器人协同制造系统和原位作业模式兴起[1-4],其在车间内部署多台机器人加工单元,通过协同作业实现复杂产品的高效率、高柔性制造。然而,多机器人系统的工作空间非结构化和分布式特性导致其协同复杂、避碰问题显著;此外,复杂产品的加工任务通常因工艺和工序要求而存在加工时序约束。为解决以上问题,同时最大化系统的加工效率,有必要对多机器人系统的加工任务调度规划方法开展研究。
加工任务的工艺、工序要求引起的时序约束,以及机器人关于任务的冲突和避碰,通常可以归类为带有时间和顺序约束的多机器人规划问题。NUNES等[5]于2017年对此类问题进行了系统性分析和归类,提出用时间窗(Time Window, TW)表示任务的时间约束,用并发和优先(Synchronization and Precedence, SP)表示任务的顺序约束。时序约束的建模和约束一致性检验是该领域中的首要问题,DECHTER等[6]提出了简单时间网络(Simple Temporal Network, STN)模型,其中用顶点表示时间窗的起止时间变量,用加权有向边表示隐含的时间代价及变量之间的不等式约束。STN规定任意两时间变量之间至多只存在一项约束,使模型很容易通过变量的不等式关系检验一致性[7-8],加之其支持动态修改和扩充的特性[9-10],使STN大量应用于调度优化问题的求解中[10-15]。NUNES等[11]将STN与连续单件拍卖算法结合,提出了能够处理时间约束任务的多机器人任务分配算法TeSSI,其核心是基于插入启发式的任务竞标机制,机器人借助STN确定不破坏时间约束并使代价函数最小化的任务及任务在时序中的插入位置;GOMBOLAY等[13-14]针对多机器人应用于飞机装配任务时遇到的时间和空间约束提出了Tercio算法,其中结合了多智能体任务调度器与混合整数线性规划,并使用STN表达任务的优先约束和时间窗宽度限制,从而得到满足装配任务工序和工时要求的调度计划。
以STN为代表的任务时序约束建模方法及其变体[16]尽管大量地应用于包括制造领域在内的多机器人任务分配/时序规划中,但认为时序约束是任务的固有性质或在优化前已经给定,如制造问题中较常见的工序要求[17]。在本文面向的多机器人协同制造系统中,除部分任务固有的并发约束外,还存在解决避碰问题所需的优先约束和机器人自身调度计划内生成的优先约束,此类约束在算法寻优前并未确定,例如两空间临近的任务互为前序均可实现避碰要求,但如何设置此部分约束才能使算法找到效率最优的结果,则仍是一个开放问题。此外,避碰的优先约束还导致了机器人之间的跨调度依赖性[18-20],且优先约束的不恰当设置还可能导致约束不一致问题[7-9],进一步增加了问题复杂度和寻优难度。
针对加工任务的时序约束存在不确定部分时,通过多机器人调度优化实现加工效率最大化的问题,本文基于带双向边的有向图提出一种时序约束表达模型,能够快速生成完整的时序约束集实例,并通过闭环检测算法高效地完成约束一致性的定性检验,从而消除死锁并处理机器人的跨调度依赖性;在此基础上通过迭代局部搜索(Iterated Local Search, ILS)迭代优化有向图模型实例,实现对约束集的搜索,从而找到支持加工效率最大化的约束集实例;为快速生成完整的机器人调度计划、减小每次迭代的计算量,采用插入启发式将时序约束模型外的无约束安全任务快速插入到机器人调度计划中,将调度计划由定性时间描述转变为定量时间描述。最后结合仿真与实验验证了上述方法在处理时序约束、提升加工效率及防碰撞上的有效性和可靠性。
1 工程需求
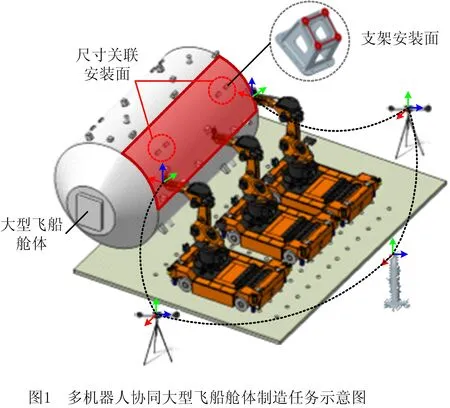
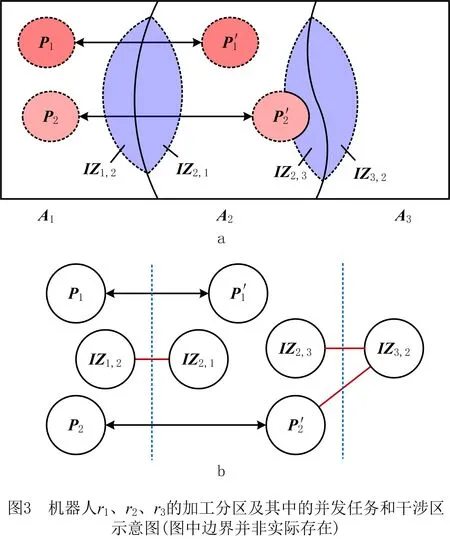
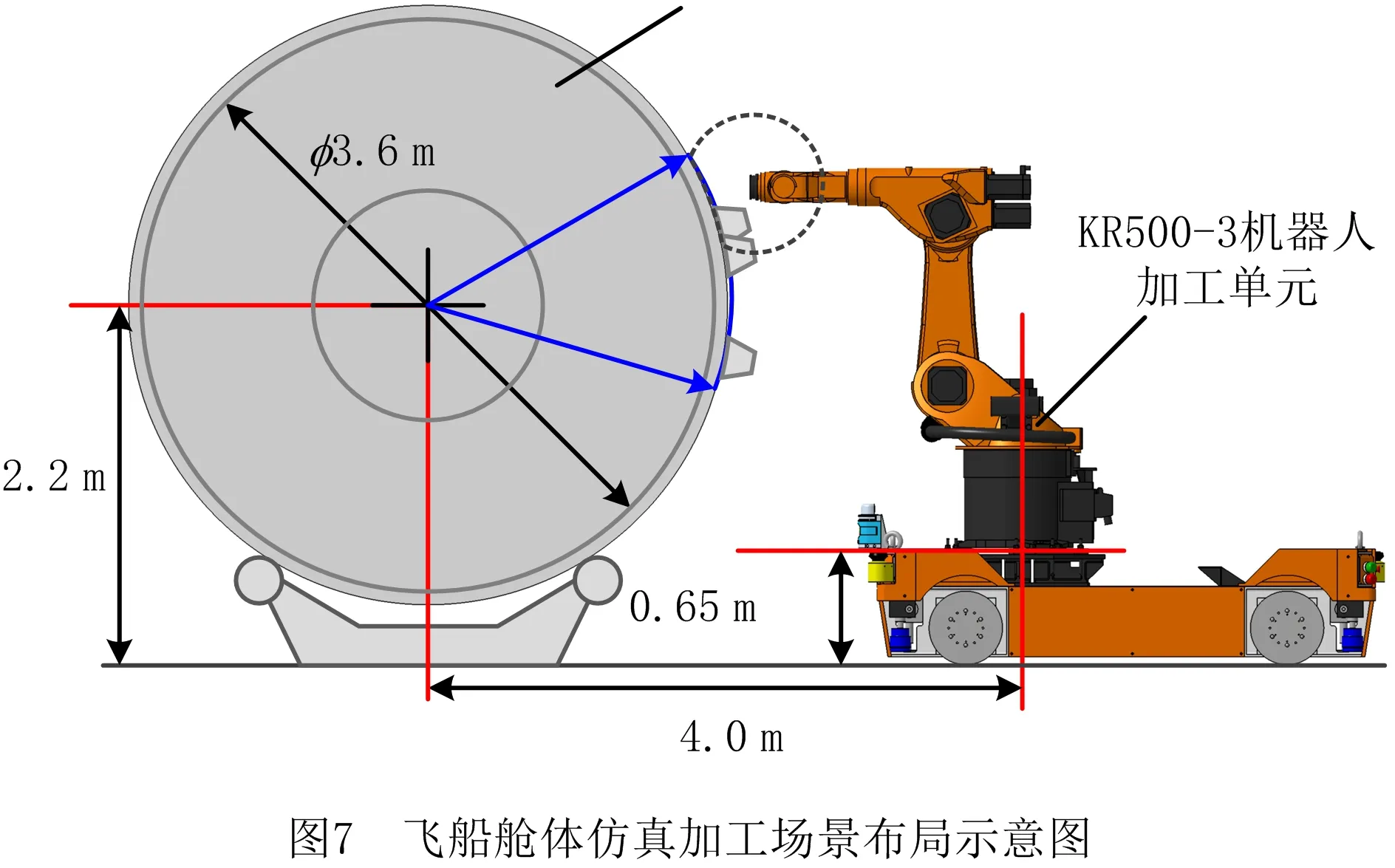
本文以大型飞船舱体表面特征的多机器人协同原位制造任务为研究对象,如图1所示。飞船舱体为一大尺寸圆柱形结构件,为安装传感器、雷达天线及空间机械臂等舱外载荷,需在其表面安装大量支架作为载荷的固定点。舱体制造任务的挑战在于舱外载荷对安装精度有极高要求,而舱体本身因滚弯、焊接等工艺原因而存在变形误差,为保证载荷相对舱体全局基准的精度,必须在支架安装于舱体表面的状态下对支架顶部的安装面进行原位测量和精加工,通过精确去除加工余量达到保证载荷最终安装精度的目标。工程中采用多机器人协同制造系统完成该制造任务,机器人每次能够处理舱体表面一定区域内的支架,舱体通过多次旋转完成全部支架的加工,本文研究内容为机器人一次协同加工中的调度优化。
2 问题建模
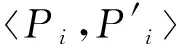

Sj=[sj,1sj,2…sj,l…]
(1)
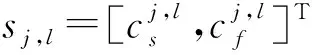
(2)
并满足以下约束:
C1:Ai⊂Trch(ri)(i∈[1,k]);
C3:∀i,j∈[1,k](i≠j),Ai∩Aj=∅;
C6:‖t(Si,c)-t(Sj,c)‖≥dr2r_min,i≠j。
(3)
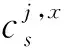
在以上调度优化问题中,并发约束是并发任务所固有的,而对于避碰问题涉及的任务(可能令机器人不满足C6的任务),其优先约束并未在问题中给定。为实现避碰目标,优化算法必须明确此类任务之间的优先约束,从而使可能引起碰撞的任务的加工时间窗完全错开。而由于能够实现避碰的优先约束通常有多种设置方式(如第1章中,令t1→t2或t1←t2均可避免机器人在t1、t2上发生碰撞),本文首先在3.2节提出一种时序约束建模方法,以获得一组可行的优先约束设置,而后在3.3节通过迭代局部搜索算法寻找使加工效率最优的约束集,从而最终明确理想的优先约束设置方式。
3 方法实现
3.1 基于任务分配的机器人分区加工
在调度规划前必须首先将任务集T分配至机器人,即首先确定任务分配TA={A1,A2,…,Ak}。任务分配期望向k台机器人平均分配任务集T的加工工作量,从而改善多机器人加工效率,为此应最小化机器人之间的工作量差距,这等价于最小化k台机器人中的工作量最大值:
(4)
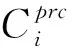

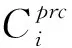
(5)
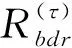
(6)
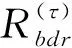
(7)
并满足约束:
C1:ta∈Aj∩Trch(ri),
(8)
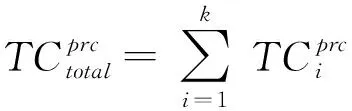
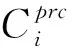
3.2 时序约束表达模型
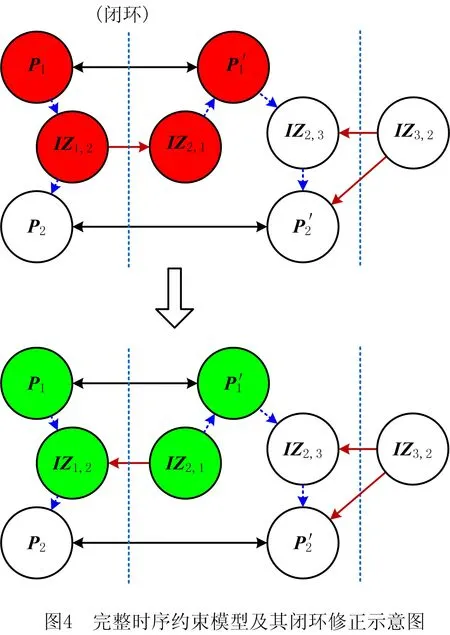
IZi={ta|ta∈Ai,∃tb∈Ak,
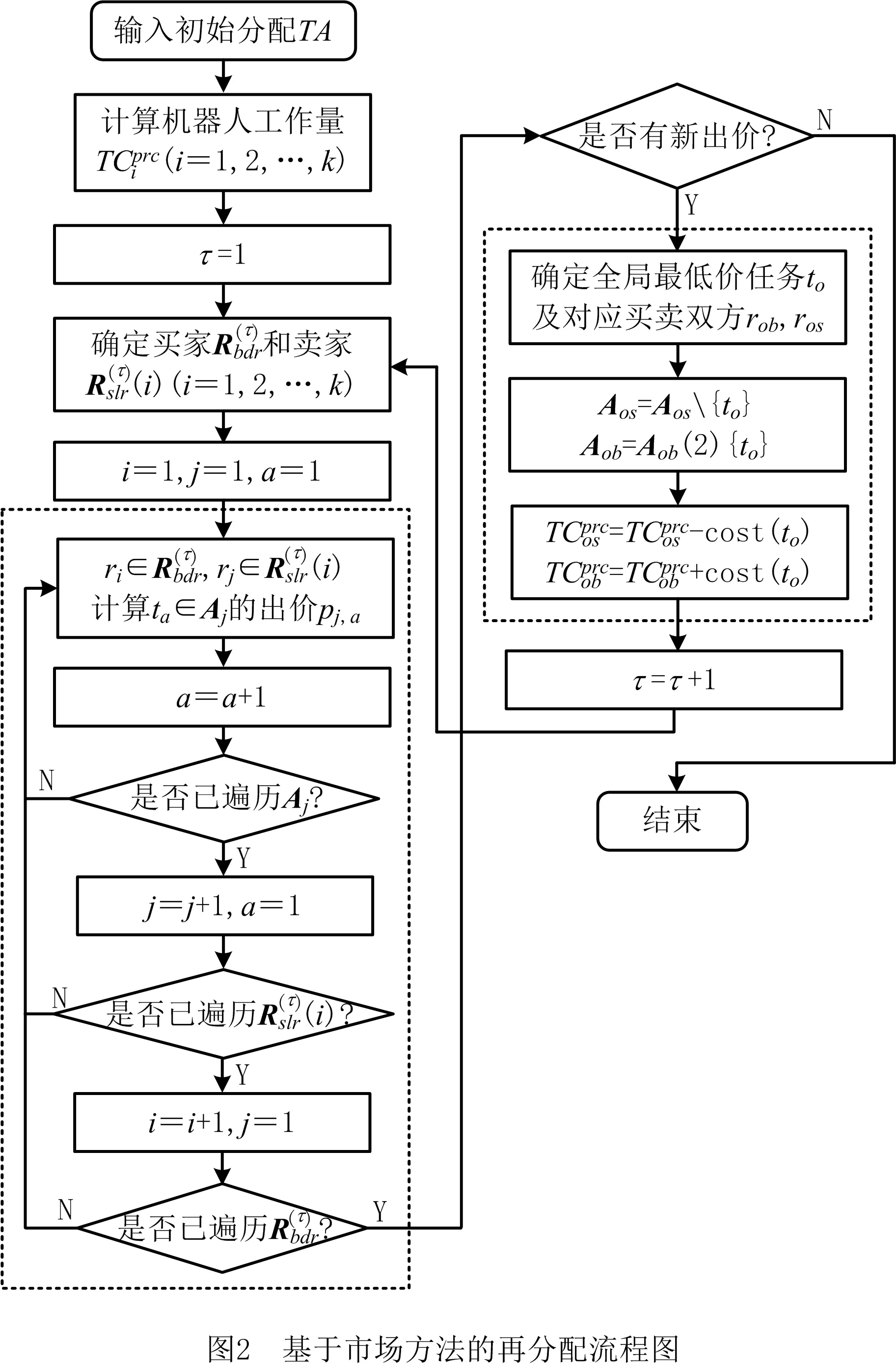
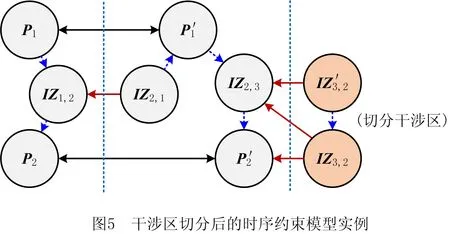
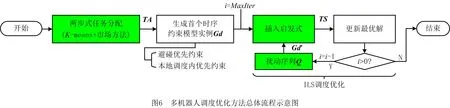
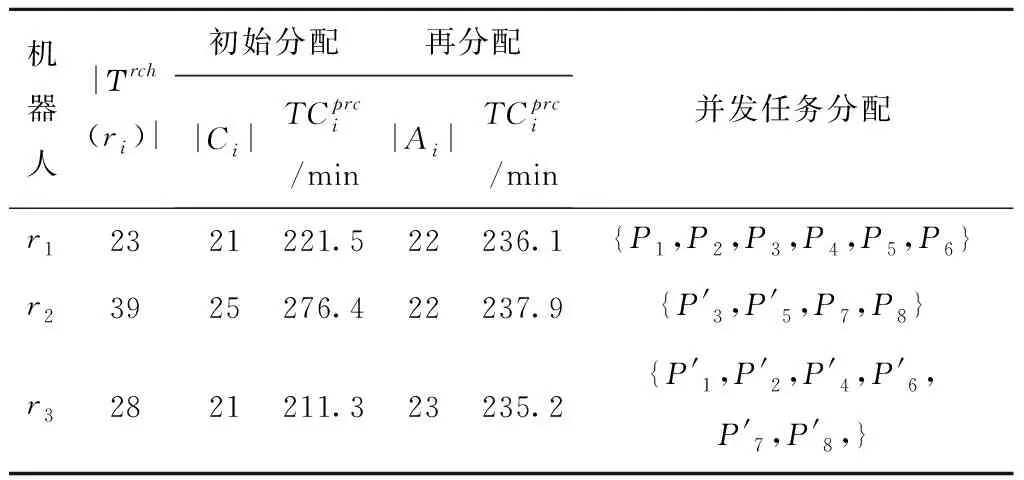
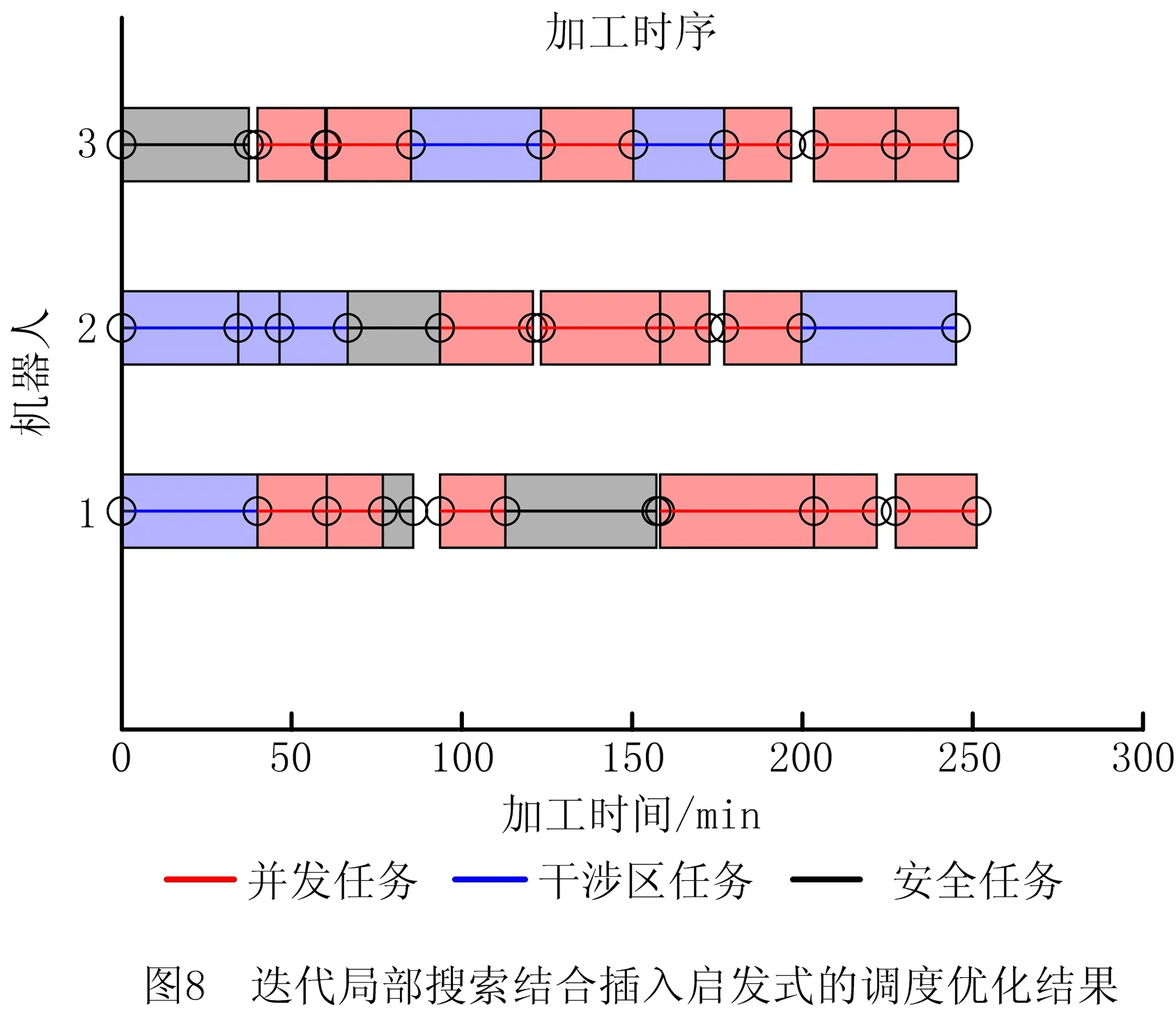
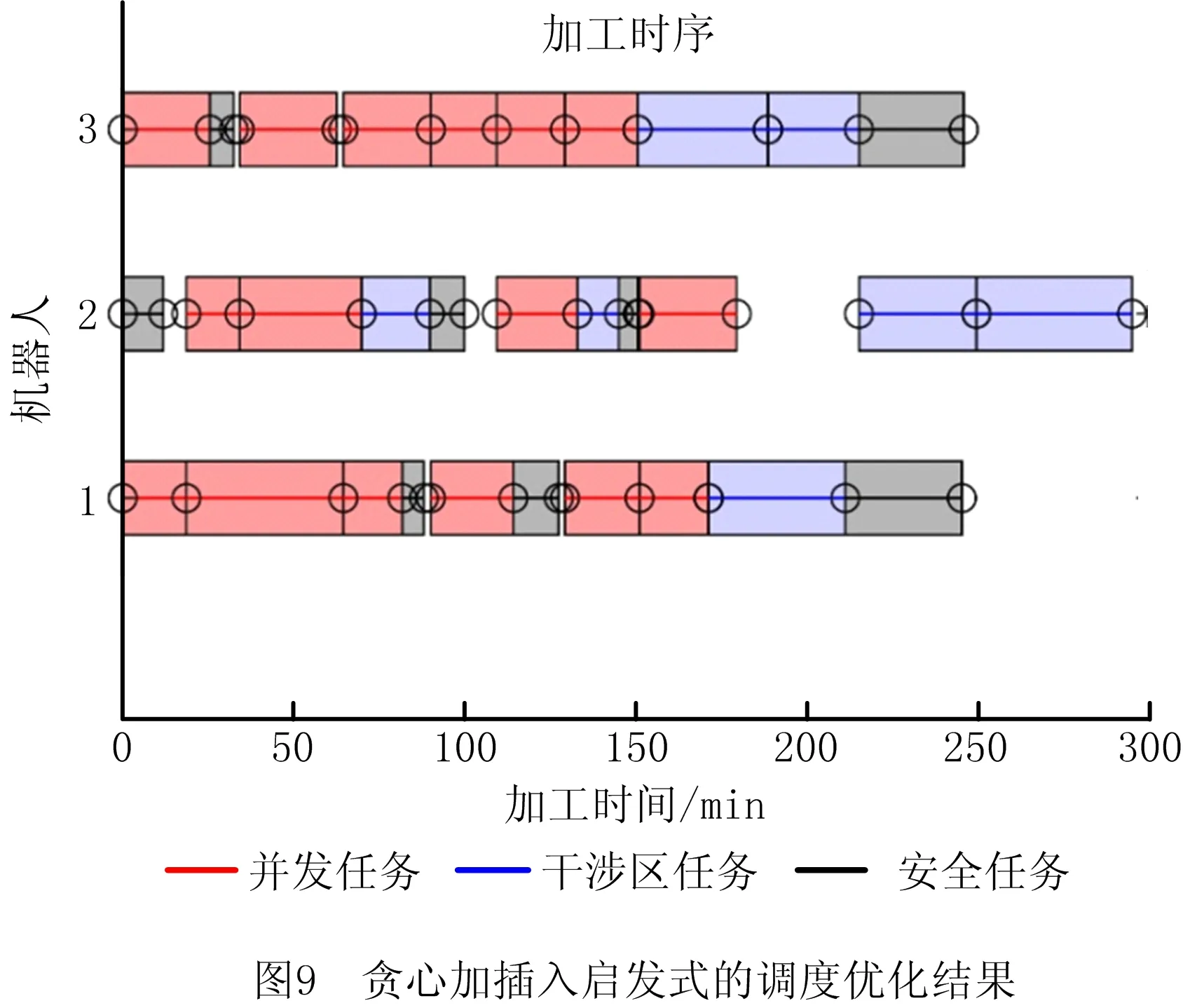
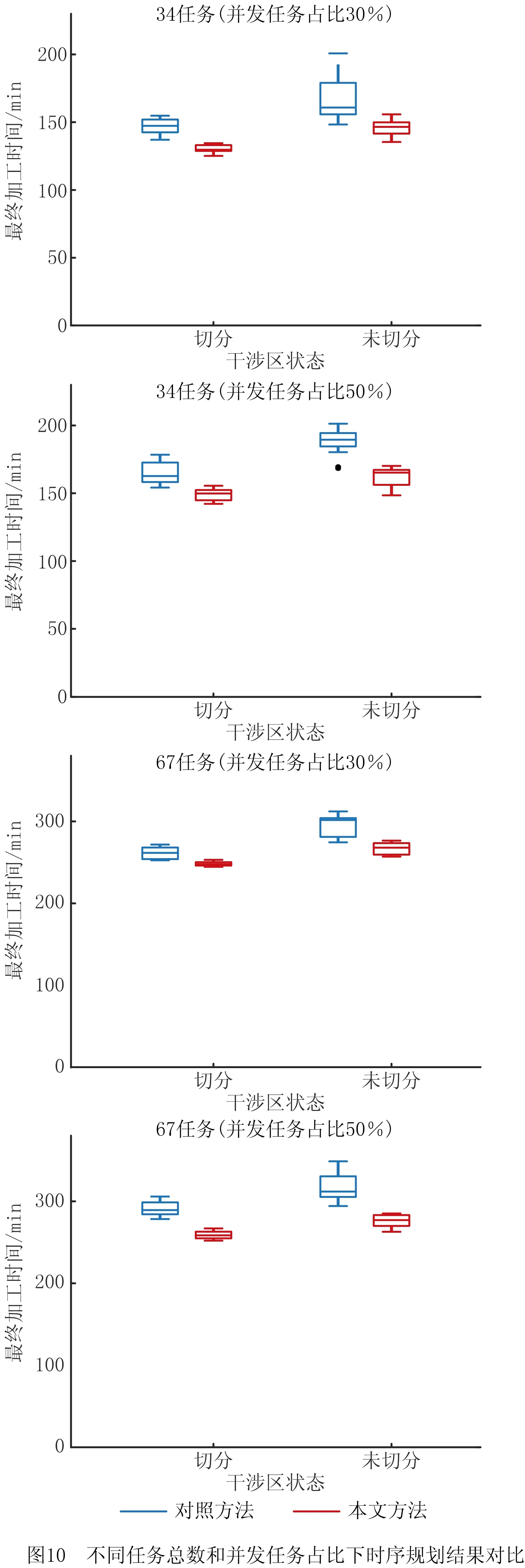
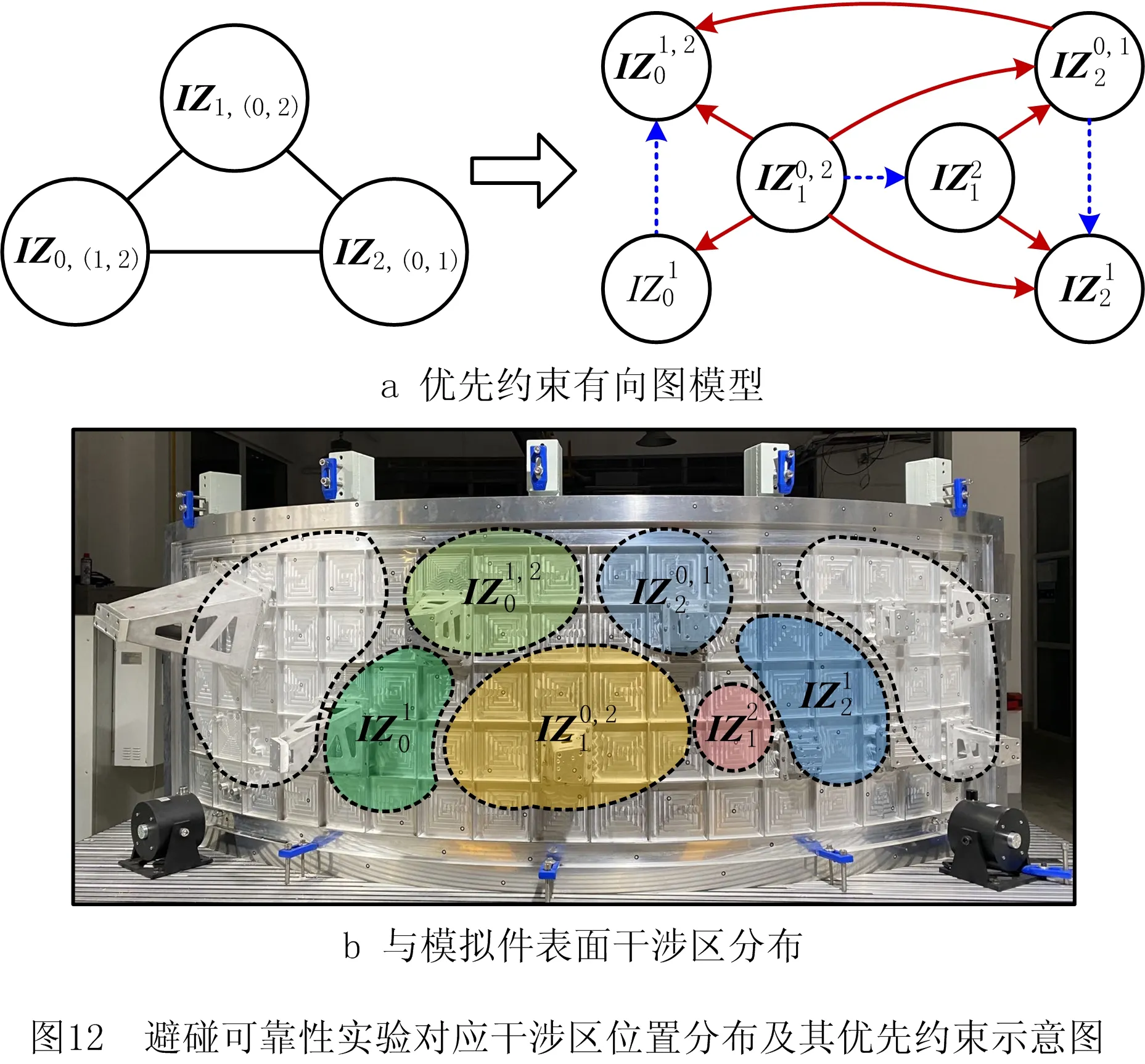
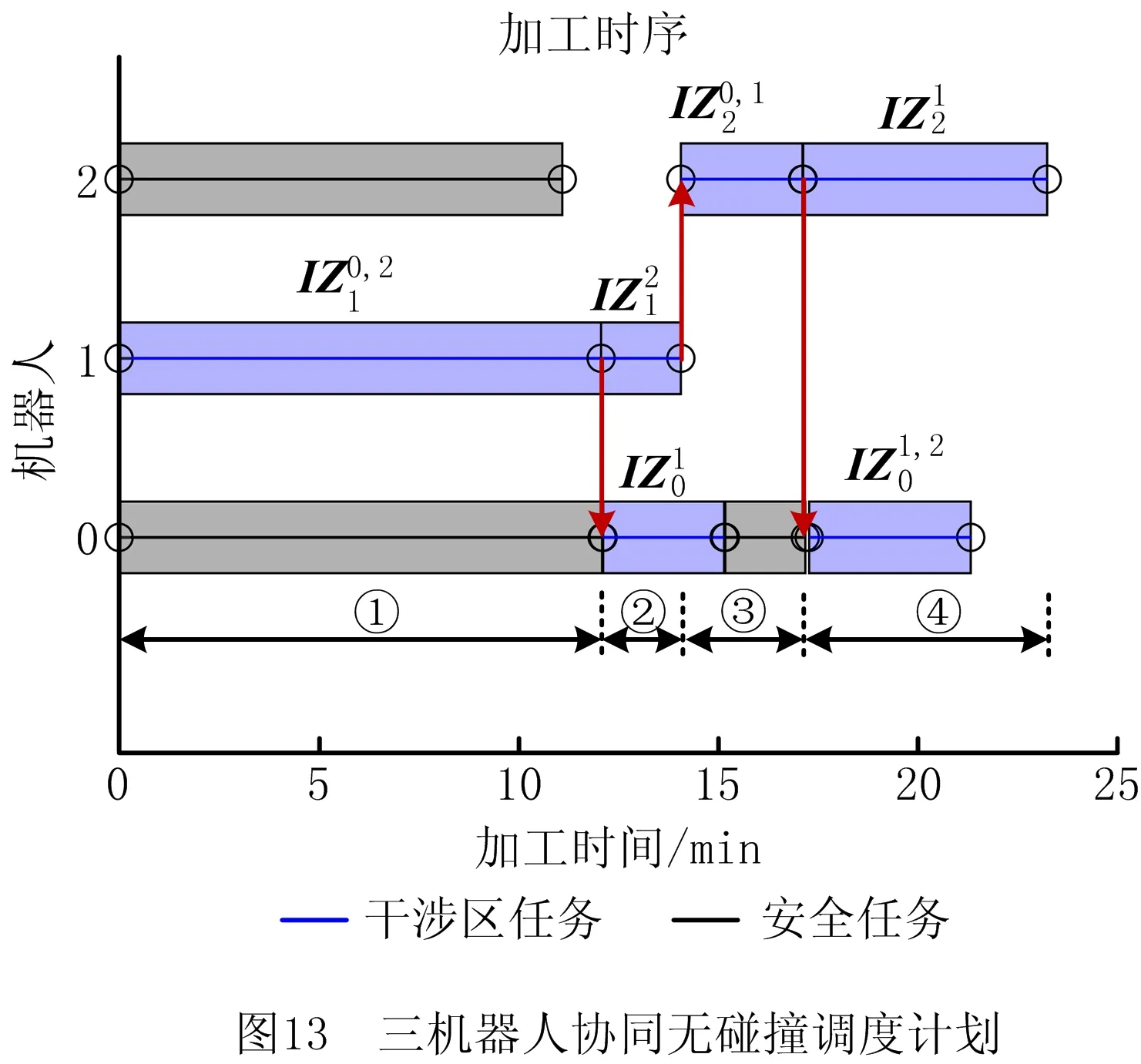
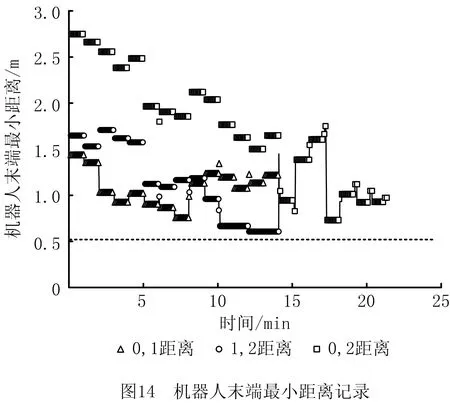
k≠i,‖ta-tb‖ (9) 为实现由Gu生成最终的时序约束模型,将全部2m个并发任务和干涉区随机排序形成序列Q,而后根据顶点在Q中的顺序确定优先约束,并在Gu中设置对应有向边: (1)当任意两顶点vi,vj之间有干涉关系,则按照顺序先后有优先约束vi→vj或vi←vj,无向边变为有向边。 (2)当两顶点vi,vj属于同一机器人rk,且两者之间没有其他顶点属于rk,则同样按顺序先后为其增加优先约束,图中增加了代表本地调度内优先约束的新有向边。 有向图的闭环检验通常可以使用深度优先搜索(Depth First Search, DFS ),为避免经典DFS直接将双向边连接的顶点误判为闭环,特别令DFS采取以下策略:当顶点有双向边连接时,总是在遍历其他路径后才沿双向边搜索。该策略能有效检验带双向边有向图的闭环,证明如下: (1)假设有向图Gd中的两顶点A、B之间有双向边连接(记为A↔B), 且A、B在某一闭环内,则必有↔以外的路径可由A到B或由B到A。 (2)对于(1)中第一种情况,即存在不依赖↔由A到B的路径,假如DFS先到达A,并在使用↔之前沿该路径来到B,则最终由B通过↔到达A,从而发现闭环。若DFS先到达B,则最终通过↔来到A,并从A发现到达B的其他路径,从而发现闭环。 (3)对于(1)中第二种情况(存在不依赖↔由B到A的路径),通过DFS发现闭环的原理与2相同。 本节参照一具体实例对所提出的时序约束模型进行说明,但该模型的应用并不受限于实例中特定的机器人数量、加工分区情况以及多机器人的布局方式,且能够反映任意两机器人之间满足并发和避碰条件的时序约束,因此有条件应用于本研究之外的其他多机器人调度规划问题中。此外,与广泛应用的STN模型相比,所提出模型的区别主要在于: (1)在所提出模型中,顶点表示某一存在时序约束的子任务集(并发任务或干涉区),而非STN中的时间变量,顶点间连接的有向边表示时序约束而非时间代价。 (2)所提出模型定性描述任务时序,并首先检验约束一致性,再根据约束确定时间变量之间的不等式关系,而在STN中,任务时序由时间变量定量描述,约束一致性直接通过时间变量的不等式关系检验。 以上特点使所提出模型相比STN能够更明确地表达两机器人之间的跨调度约束(如并发和避碰),由于约束一致性检验与时间变量的赋值分开进行,使该模型易于在原有实例上不断产生新实例,从而快速搜索不同的可行约束集,且时间变量的赋值过程简单。以上特性使该模型能够配合3.3节提出的算法高效进行多机器人的调度优化。 在确定并发任务和干涉区的起止时间变量后,采用插入启发式算法将各机器人的安全任务加入到调度计划中,形成初始解。算法将遍历问题中的所有安全任务,并计算每个任务插入到其所属机器人的并发任务或干涉区前后造成的总时间代价增量ΔTCglb,选择ΔTCglb最小的任务插入到对应插入位置上,通过迭代上述过程即可将所有安全任务加入调度计划。ΔTCglb定义为插入后调度计划的总时间跨度与插入前的总时间跨度之差。以图4为例,具体过程如下: (1)遍历A1中的安全任务并将其插入到调度计划中的3个位置:P1之前、IZ1,2之前和之后,计算整个加工过程的总时间代价增量ΔTCglb。若在前方插入任务导致P1或IZ1,2的开始时间延迟,则需更新Gd中所有顶点的时间变量。 (2)以同样方式处理A2中的安全任务,而后从中找出ΔTCglb最小值所对应的任务和插入位置。当ΔTCglb最小值非唯一时,则机器人路径代价最小的插入方案为优胜。 (3)执行插入,并更新调度计划S1、S2,以及检查更新Gd中所有顶点的时间变量。 (4)重复(1)~(3)直至A1和A2中都没有剩余安全任务。 在插入启发式形成完整调度计划后,为了充分搜索可行约束集E,达到优化加工效率的目的,采取了迭代局部搜索(ILS)策略,通过驱动约束模型Gd迭代优化约束集E,找到使加工效率最优的E的实例,继而找到效率最优解。基于某一Gd实例的插入启发式可以视为对问题解空间的一次局部搜索,ILS则通过对局部搜索产生的解施加扰动,使其变为解空间邻域上的某一点,从而帮助局部搜索过程跳出局部最优并搜索解空间中新的区域,增加找到更优解乃至最优解的机会[21-22]。在本方法中,扰动为对序列Q的随机更改:通过随机调转Q局部随机数量顶点的排序产生新的序列Q′,继而可通过Q′产生新的Gd实例Gd′和新的约束集E′。在此基础上重新执行插入启发式即可获得问题的新解。ILS总是立即接受当前最优解,并在当前最优解上施加新的扰动,直至迭代过程结束。本研究方法的总体流程图如图6所示,ILS过程启动后会不断搜索新的时序约束模型实例,直至达到预设的最大迭代次数。 4.1.1 仿真场景设计 4.1.2 多机器人任务分配 采用两步式任务分配为3台机器人分配任务集T,聚类初始分配与市场方法再分配的结果如表1所示。可见,再分配很好地平衡了机器人之间的工作量,使3台机器人之间的最大工作量差距仅为2.7 min;此外,8组并发任务也完成了分配,其中r1与r2协同完成2组、r1与r3协同完成4组,r2与r3协同完成2组。 表1 加工任务集T分配结果 4.1.3 对照方法 目前工程应用上采用一种贪心加插入启发式的调度方法,分3个阶段分别规划并发任务、干涉区任务和安全任务的加工时序: (1)首先使用贪心策略调度并发任务,根据最早开始的原则为多机器人指派第一组并发任务,且每当出现两台机器人待机时都立即尝试为其指派新的并发任务,直至全部并发任务加入调度计划。 (2)采用插入启发式策略,寻找使总加工时间增量ΔTCglb最小的干涉区及对应插入位置,从而向调度计划中增加干涉区任务,直至全部干涉区都插入。 (3)仍采用插入启发式策略,寻找使总加工时间增量ΔTCglb最小的安全任务及对应插入位置,直至3台机器人的全部安全任务都插入到加工时序中。 以上策略的详细规则设置如表2所示,确保该调度方法的行为较为合理高效。 表2 对照调度方法所采取策略的详细设置 4.1.4 仿真结果与分析 以任务分配结果为输入,采用本文提出的方法进行调度优化,工程应用方法则作为对照,其中本文方法共搜索200次,结果分别如图8和图9所示。两图中红蓝灰三色条带代表了并发任务、干涉区和安全任务的加工时序,条带间的空隙则表示机器人出现了停顿。本文方法最终加工时间为251.5 min,最后完成加工的机器人为r1,其非加工时间为15.4 min;对照方法最终加工时间为295.4 min,最后完成加工的机器人为r2,非加工时间达到了57.5 min。相比对照方法,本文方法使加工时间缩短约14.9%。本文方法最终形成的加工调度中,机器人交替执行并发任务和干涉区任务,且各机器人均没有显著的停顿时间;而对照方法通过贪心策略先行确定并发任务的加工时序,尽管并发任务的加工时序较为紧凑,但随后的插入启发式策略无法为干涉区任务找到紧凑的加工时序,导致位于中间位置、避碰问题最复杂的机器人r2出现了显著的停顿时间,降低了整体效率。 为直观分析加工调度的效率,此处借鉴文献[23],将加工调度的效率定义为任务分配后多机器人中出现的最大工作量与完成最后一个任务的机器人所用的总时间跨度之比,即 (10) 其中:i=1,2,…,k;当机器人的加工调度中不存在任何停顿时,e=100%。由表1可知,3台机器人中出现的最大工作量为r2的237.9 min,则本文方法与对照方法所产生加工调度的效率分别为94.6%和80.5%,本文方法带来的调度效率提升为:(0.946-0.805)/0.805×100%=17.5%。由于加工调度的效率已接近95%,可知本文方法的寻优性能较好,结果所剩优化空间已较小。 由于本文所提出的调度优化算法本质上是一种启发式算法,需要检验其鲁棒性,即是否总能在有限次迭代中稳定地找到较优解,以及在优化问题的要素(如任务数量)发生变化时性能是否仍然稳定。为此设置34和67两种任务总数以及30%和50%两种并发任务占比,共生成4组不同的随机任务集,每组包含50个随机实例,支架在舱体上的分布位置需随机生成,加工时间在5~15 min之间随机指定。在任务分配后,采用两种方法分别计算全部200个任务集实例,其中本文方法的最大迭代次数仍设为200次;将4组规划结果对应的加工时间分别用箱线图表示,结果如图10所示。 箱线图中箱体的横线对应数据的中位数和上下四分位数,因此箱体位置反映了数据的分布。从图中可见,本文方法在不同条件下所产生的优化结果总是优于对照方法,且箱体更扁平,反映了算法寻优的稳定性和可靠性较好、受调度问题本身的影响更小。通过观察还得出以下规律: (1)在任务总数相同时,并发任务比例的增加使两种方法产生的最终加工时间均增加。表明并发约束增多导致寻优的困难性增加,但本文方法所产生的结果增幅相对更小。 (2)通过切分干涉区来降低时序优化难度的手段在不同条件下均有一定效果,且对照方法的性能对是否切分干涉区更加敏感。 保证多机器人避碰安全是调度优化方法的基本功能,为验证其可靠性,基于实验室内舱体模拟件设计了一避碰问题较复杂的多机器人加工场景,并使用两种不同的机器人试验平台进行了实机验证,如表3所示。表中的最大可达距离系机器人本体腕关节的最大可达距离,系对比机器人的规格差异,实验中机器人对任务的可达性并非基于此参数进行判断。 表3 试验平台机器人规格 舱体模拟件模拟了直径约2 m的大型舱体局部,宽2.73 m,高1.0 m,表面设置48个虚拟支架。实机验证平台布局如图11所示,AUBO-i5机器人位于中央,中线与模拟件中线对齐,两台KR60-3 HA机器人则对称布置于AUBO机器人的两侧,将其按图11由左到右分别命名为r0,r1和r2。该布局令3台机器人的工作包络相互重叠,3台机器人可能同时发生冲突,增加了避碰问题的复杂性。该场景可模拟大型舱体制造中加工机器人与辅助机器人协同的情况,其中r1用于承担辅助性任务,如搭载视觉跟踪设备或夹爪进行精度补偿或支架零件装调等任务。 3台机器人由同一台工控机控制,规划结果对应的运动指令由上位机生成并发送至机器人,与机器人控制器的通讯则通过TCP/IP经由网络交换机实现。实验中,末端之间的最小安全距离dr2r_min=0.52 m,r0和r2完成每个任务所需的时间设为1 min,而r1为2 min。实验前通过计算机器人工具坐标系关于任务目标位姿的运动学逆解来判断机器人对各加工任务的可达性,从而建立各机器人的可达任务集Trch(ri)(i=1,2,3),以便实施任务分配。r0,r1和r2的工具坐标系均设在法兰坐标系沿自身X轴正方向平移0.3 m处。任务分配结果见表4,其中r1因可达性限制只能加工7个任务,该结果已最大限度地平衡了机器人工作量差距。 表4 实机验证机器人任务分配结果 本节实机验证中的3台机器人彼此均可能发生碰撞,r0,r1和r2的干涉区写作IZ0,(1,2),IZ1,(0,2)和IZ2,(0,1),表示其中的任务分别与两个队友的任务干涉(如图12a左)。以上干涉区同样采取切分策略来细分避碰所需的优先约束,实施规则为:原干涉区中仅与特定队友存在干涉的任务可构成一个独立的干涉区。具体结果如下: 切分后形成的6个干涉区及其在模拟件表面的分布情况如图12所示,其中的白色区域表示r0和r2的安全任务所在的位置。 使用本文提出的算法对3台机器人的干涉区和安全任务进行时序规划,经过28次迭代后,调度计划的效率已达到90%以上,遂停止迭代。最终确定的干涉区优先约束集如图12a右所示,具体加工时序则如图13所示,图中标出了6个干涉区对应的时序以及实现避碰的优先约束;以上调度计划预计所需加工时间为23.27 min,最后完成加工的机器人为r2。整个实机验证过程最终用时23.83 min,相比时序规划预计的总时间略增加了33 s,其原因除机器人加减速过程使实际移动速度并非规划时的固定值外,还与机器人的加工时间波动导致部分干涉区的完成时间滞后、增加了队友停顿时间有关。在以上验证过程中以1 s为时间步长采集3台机器人末端执行器TCP的空间位置,并计算两两之间出现的最小空间距离,结果如图14所示,其中虚线代表dr2r_min的值(0.52 m),可见r0,r1和r2在整个加工过程中都满足了避碰要求,在约第12~14 min,r1和r2之间出现了全局最小距离0.61 m,其余时间中,3台机器人的末端TCP之间的距离均显著高于dr2r_min,证明了机器人加工全过程的操作安全。在约21分20秒后仅剩r2仍在运行,而r0、r1已返回HOME姿态,因此不再计算r2与r0和r1的距离。 以上实验证明了本文的调度优化模型和算法在处理机器人避碰问题上的可靠性,且当机器人的加工时间相对规划时间出现波动时仍能够保证实现避碰,表明本方法有一定的鲁棒性,具备工程应用条件。此外,基于干涉区进行的调度规划使机器人在多数运动过程中都保持较充足的距离,有助于减少离线编程时为两个安全间距偏低的机器人进行精细轨迹规划的工作量,提升了编程效率。 针对多机器人协同制造系统处理航空航天复杂产品时的多机器人避碰问题、加工任务时序约束,以及加工效率优化问题,本文提出一种加工任务时序约束的建模方法和调度优化算法。首先采用带双向边的有向图建模和表达任务集中的干涉任务、并发任务以及对应的优先和并发约束,继而通过有向图的闭环检测实现了时序约束一致性检验,闭环检测则通过改造深度优先搜索算法得以实现;提出结合插入启发式的迭代局部搜索算法实现机器人调度优化,其中迭代局部搜索算法用以驱动时序约束有向图模型不断搜索新的约束集,插入启发式则用以在给定约束集下快速构建完整的机器人调度计划。仿真结果证明所提出的模型和算法相比目前工程应用的方法显著提升了加工效率,同时结果满足了多机器人避碰要求和加工任务的并发约束;算法鲁棒性测试表明本文提出的算法在任务规模和时序约束复杂程度发生变化时仍能稳定地找到机器人调度计划的较优解。此外,在实验室条件下进行了三机器人调度避碰实验,实验结果表明本文所提出方法能可靠地处理机器人避碰问题,并对加工时间的波动具有一定鲁棒性。 在本文工作基础上,未来应进一步考虑机器人随机故障/换刀、特征加工余量在线检测等制造现场复杂扰动和不确定因素,研究能够处理不确定性和随机事件的时序规划算法和模型,以便形成在线决策和实时优化能力,进一步提升多机器人在复杂制造任务中的智能化水平和鲁棒性。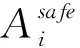
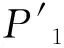
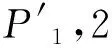
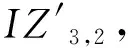
3.3 结合插入启发式的迭代局部搜索
4 仿真与实验分析
4.1 时序约束任务调度优化仿真
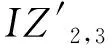

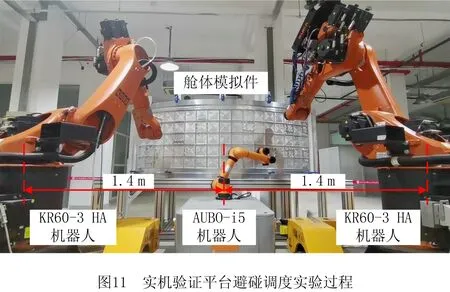
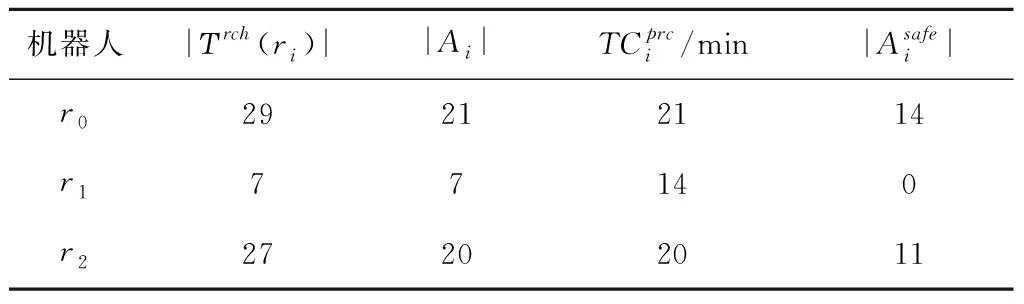
4.2 避碰可靠性实机验证
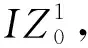
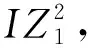
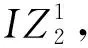
5 结束语

