考虑岩石强度尺寸效应的脆性地层井壁坍塌压力统计模型

邱康，褚道余，王颖，李乾，熊振宇，李基伟，崔强

（中石化海洋石油工程有限公司，上海 200120）

井壁失稳一直是困扰钻完井施工的难题之一，自上世纪四十年代开始即被广泛研究，相关研究重点针对井筒应力分布、岩石本构关系及弹塑性破坏准则、流体与岩石相互作用、井眼形态对井壁稳定影响等方面。井筒尺寸等宏观几何特征对井壁稳定影响关注较少，从钻井实践来看，同样地层随着井眼尺寸的增加，井壁是趋向于更不稳定，具有明显的尺寸效应，根本原因是不同井眼揭露的井壁上的缺陷不尽相同。

对于岩石尺寸效应，浅层岩石力学或者混凝土等类岩石材料相关专业研究较多，从目前研究结果来看，普遍认为岩石等准脆性材料具有明显的尺寸效应现象，即岩石的力学参数，如单轴强度、内黏聚力、摩擦角、断裂能、断裂韧度以及临界应变能释放率等并非常数，而是随着几何尺寸的不同而发生改变，原因主要在岩石内部裂纹、节理及弱面等缺陷导致的非均质性[1]，但不能简单理解为随着岩石尺寸的减小，所含缺陷越少，从而强度越大[2]。岩石非均质性复杂程度导致严格按照实际进行微观结构描述是不可能实现的。因此目前针对岩石等准脆性材料尺寸效应的理论有非常多，包括Weibull统计理论、Bazant基于能量释放的尺寸效应律、基于分形损伤力学的尺寸效应等[3-5]。这些理论大多需要对比一个假设的标准尺寸下的强度参考量，工程应用的适用性有待于进一步拓展；同时通过岩心样本强度实验来拟合岩石强度与几何特征关系的研究也开展的比较多，岩样的几何特征主要包括直径、长径比等，模型准确性受岩样本身强度离散性以及样本数量等影响较大，其中，刘宝琛等基于国内外岩石抗压强度尺寸效应实验结果建立的经验公式更符合对尺寸效应的一般认识[6]。引用实验建立的岩石强度尺寸效应拟合模型，刘书杰、陈朝伟等建立了针对小井眼的考虑尺寸效应的井壁稳定模型[7-8]，刘书杰等采用了强度尺寸效应指数模型建立的模型并没有考虑内摩擦角本身的尺寸效应[7]，陈朝伟等采用了刘宝琛等建立的强度尺寸效应拟合模型，但简单的采用了井径来代替小岩样的尺寸也是不合理的，强度模型中的岩体强度、无缺陷强度获取难度大。

1 考虑岩石强度尺寸效应的脆性地层井壁坍塌压统计模型

岩石尺寸效应主要在于其非均质性，其内部存在裂纹、节理及弱面等缺陷，材料内部的缺陷决定于微观结构及其失效，其分布决定了材料局部的宏观强度，这是统计方法的物理基础。这种研究方法，避开严格地对材料微观结构进行研究的困难，通过对微观结构中一些影响强度的主要因素做某些简化假设，用概率统计的方法来研究微观结构的综合作用，从而求得宏观的强度值是可行的[5]。设单位体积的岩石材料在应力 σ附近的缺陷密度函数为n(σ)，则在单位体积中，累计的缺陷数目为：

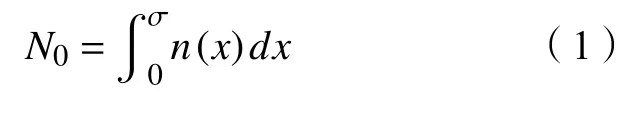
体积V的材料中的缺陷数为：

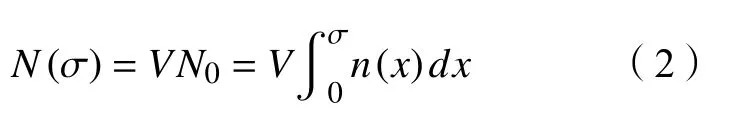
假设材料的微观力学性能服从Weibull 分布，其概率密度函数为[9]：

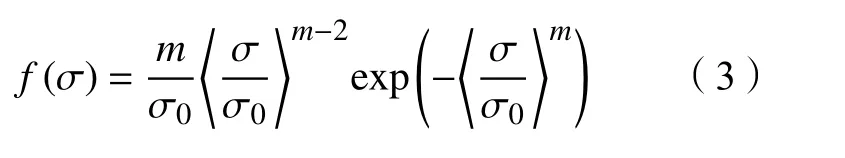
式中：〈·〉为McCauley 括号；σ0为强度参考尺度；m为 Weibull 模量，表征材料的均质性，m＞1，m越大表示材料越均匀。

由最弱环理论，体积V的岩石中含N(σ)个缺陷破坏的概率为[10]：

岩石破坏的平均应力可以表示为：

将式（4）带入式（5），岩石的平均强度用Gamma函数表示为：

式中：Γ(·)为Gamma 函数。

在极坐标下，井周微元可以表示为：

对照式（6）、式（7），岩石的平均强度，即单轴抗压强度可以近似表示为：

对于脆性地层，井周围岩的剪切破坏满足库伦准则：

式中：σ1、σ3为最大、最小有效主应力，MPa；为岩石的压拉比。

对于直井而言，按照平面应变理论，井周围岩的剪切破坏一般首先发生在井壁上井周角或者处，在不考虑渗流作用时，该处周向应力和径向应力分别为最大和最小主应力[11]：

式中：σr、σθ分别为井周径向应力、周向应力，MPa；σH、σh分别为最大、最小水平地应力，MPa；Pp为地层压力，MPa；pi为井筒内压力，MPa。

将式（8）、式（10）、式（11）带入式（9），可以求得维持井周围岩不发生剪切破坏的最小井内压力，即坍塌压力：

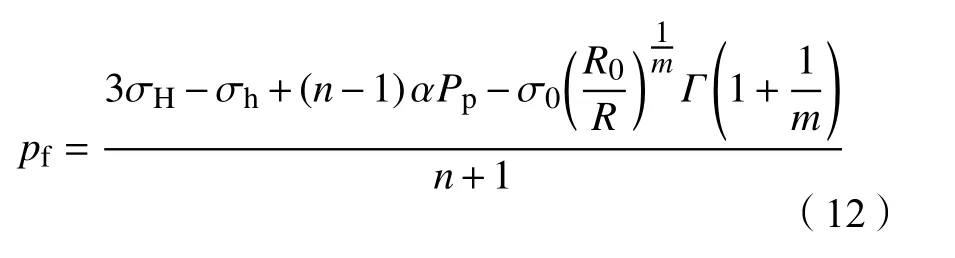
考虑井周弹性模量修正[11]，坍塌压力改写为：

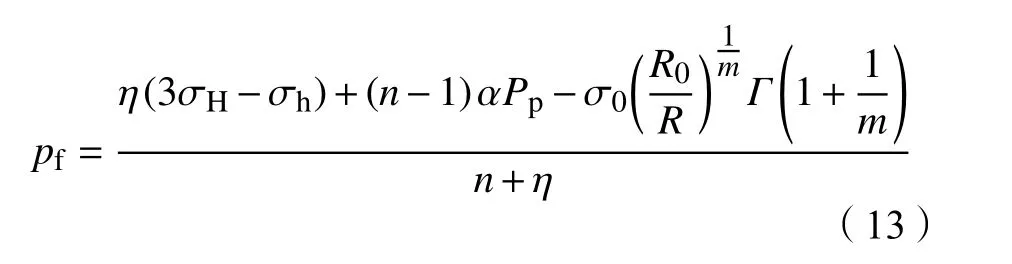
式中：η为非线性修正系数，一般取0.95。

对于钻井工程，一般习惯用当量密度来表示坍塌压力，即：

式中：H为井深，m。

2 模型参数确定及影响因素分析

式（14）在求解过程中，存在三个难点，分别是不均匀系数m、标尺强度 σ0和压拉比n。不均匀系数m与井周裂隙、节理分布密度等有直接的关系，无法直接用测井数据评价得到，假设岩样的表征和井周围岩是一致的，可以通过三组不同长度的单轴强度室内实验，利用式（6）得到。对于标尺强度 σ0，在室内实验岩样中，可以选取标尺尺寸的岩样后求得，即令V0=V，带入式（6）后，标尺强度可以表示为[5]：

在获得标尺尺寸的岩样单轴抗压强度后，即可获得标尺强度 σ0，但是这个标尺强度受到形状差异的影响，并不能直接用于式（14），在实际应用的过程中，可以选定现场常用的某一井眼尺寸作为标尺尺寸R0，通过现场实践得到的维持井壁稳定的当量密度，由式（14）反算该井眼对应的标尺强度，即：

对于压拉比n，认为岩石抗压强度和抗拉强度的尺寸效应是一致的，也可以通过室内实验获取，对于砂岩而言，一般为7～39[12]。

以东海盆地某井参数为例[13]，H=3 000 m，σH=61.3 MPa，σh=55.7 MPa，Pp=30.3 MPa，α 、η均取0.95，标尺井径取6″，标尺强度σ0=25.6 MPa，压拉比n取9。图1为不同不均匀系数条件下，坍塌压力随井径变化规律，可以明显看出，随着井径增加，坍塌压力随之增加，符合一般钻井施工认知规律，并且随着井径增加，坍塌压力增加幅度有所下降，表明随着井径增大，井径对坍塌压力影响程度有所下降。

图1 不同不均匀系数条件下坍塌压力随井径变化规律Fig.1 Variation of collapse pressure with well diameter under different inhomogeneity coefficients

结合图2，可以看出不均匀系数在井径对坍塌压力中起到了关键作用，随着不均匀系数增加，岩石区域更加均匀，坍塌压力受到井径影响明显减弱，根据式（8）可知，在非均匀系数无限大的条件下，岩体强度趋向于均匀岩石强度，坍塌压力不再受到井径影响，表明在岩石均匀程度较高情况下，井眼尺寸对坍塌压力的影响相对较小，裂隙等缺陷较为发育的地层，井眼尺寸对坍塌压力的影响不应该被忽略。

图2 不同井径条件下坍塌压力随不均匀系数变化规律Fig.2 Variation of collapse pressure with inhomogeneity coefficient under different diameters

压拉比作为一个比较直观的代表岩石强度参数，实际上也包含了岩石非均匀系数的影响。图3给出了在井径为9-1/2″，不均匀系数为3 时，不同压拉比对坍塌压力的影响。可以看出随着压拉比的增加，坍塌压力降低明显。

图3 压拉比对坍塌压力的影响Fig.3 Influence of compression and tension ratio on collapse pressure

3 结论与认识

在基于统计岩石强度尺寸效应模型讨论的基础上，建立考虑岩石强度尺寸效应的坍塌压力模型，探索模型参数确定方法，并且利用实例讨论关键参数对模型的影响，主要结论如下：

（1）基于统计的岩石强度尺寸效应模型建立的坍塌压力模型，能够描述井眼尺寸对坍塌压力的影响，算例结果表明随着井眼尺寸增加坍塌压力增加，但增加幅度有所下降，符合一般钻井施工认知。

（2）本文采用相对简单的以压力比和单轴抗压强度为主要强度参数库伦准则，没有考虑实际条件下的三维应力条件，从目前研究来看，内摩擦角和黏聚力等强度参数也具有明显尺寸效应，但仅能通过实验数据回归简单的模型来描述，很难通过理论方法建立模型，相关研究仍需要进一步开展。