不同金属材料转向垂臂疲劳仿真分析

许冬，彭宝营，王鹏家

(北京信息科技大学 机电工程学院，北京 100192)

0 引言

转向垂臂作为汽车传动机构的重要零部件以及车辆转向系统的重要组成部分，主要是将传动机构的转向柱或者转向轴的径向运动转化为线性运动，以此来控制车轮的转动。由于转向垂臂是3个角旋转连杆中的第一个，主要负责将转向器的输入传递给转向横拉杆，依次控制左右转向横拉杆及其各自的车轮，一旦转向垂臂出现磨损或损坏时，可能会导致严重的转向失控进而威胁驾驶员的安全，这使得任何车辆维护方案都必须定期检查和维护这一关键部件。目前对汽车转向垂臂的研究大多数集中在优化自身结构上，关于不同材料的转向垂臂性能对比方面研究相对较少。

目前，大多数零部件会借助有限元分析为实际应用提供理论分析和参考。阮景奎等[1]通过建立数学模型，并以该模型的控制参数作为设计变量，采用遗传算法对转向垂臂进行了一系列的尺寸优化；罗来马等[2]利用各种表征手段对汽车转向器垂臂失效原因进行了分析，发现了汽车转向器垂臂失效的原因是其内部显微组织出现缺陷以及硬度太低；彭树陈[3]通过有限元分析软件对转向臂进行静力学分析，获得了转向臂的应力大小以及分布状况，并对应力集中的部位进行优化和改进设计；王佩瑶等[4]利用拓扑优化技术建立了转向垂臂的拓扑优化模型，在优化后的基础上对其进行二次设计；陈明媚等[5]对转向垂臂进行结构和受力分析，通过改变其结构来提高强度，从而达到减少变形的目的；赵振全等[6]利用SolidWorks软件对转向臂进行建模和有限元分析，得到转向臂的受力情况和应力分布情况；王小平等[7]对转向臂结构进行了CAE设计分析和计算,从结构和可靠性两个方面对原始设计结构进行了分析和优化；韦洲等[8]利用ProCAST软件对熔模铸造的转向臂进行设计,采用ANSYS软件对铸造成形的转向臂进行有限元分析；马世野等[9]使用有限元软件对转向垂臂进行分析计算,确定其设计合理性。

综上所述，目前对于汽车转向垂臂的研究大多数集中在结构优化上，关于不同材料的转向垂臂进行性能(强度、刚度、形变、使用寿命等)对比研究相对较少。由于实际试验需要消耗大量时间、人力以及材料，为了避免时间、人力和材料的浪费，因此使用有限元分析技术为后续实际试验和应用提供理论参考。本文以某型汽车的转向垂臂作为研究对象，通过有限元技术分析对比40钢、40Cr、20CrMo和TC4钛合金4种材料的总变形、最大应力与寿命和安全系数，为转向垂臂材料的合理选择提供理论参考。

1 转向垂臂的载荷计算

当汽车在正常驾驶过程中，需要对汽车转向盘施加一个力矩，该力矩会由汽车转向轴传递至转向器，经过减速增力传给转向垂臂，由转向机构的转向纵拉杆传给转向节上的转向节臂，使转向节和它所支撑的车轮发生转动。当汽车转向时，会产生汽车转向阻力矩MS，该阻力矩是以汽车在静止状态下为标准来进行计算。因为在汽车转向时，最大转向阻力矩是出现在原地转向，且转向轮在原地转向时需要克服与地面的静摩擦力以及转向轮绕主销转动的阻力等。同时汽车轮胎受到的阻力也是通过转向节传递，最后作用在转向垂臂上。

本文针对某型汽车转向垂臂进行分析，其汽车转向阻力矩的计算可以根据苏联的半经验公式(1)得出：

(1)

式中：μ为轮胎与地面的静摩擦系数，μ=0.6；G为一侧车轮负荷，G=33 400 N；P为车轮胎压，P=7.3 MPa，代入可得：

MS=1 438.7 N·m

当遇到阻碍物车轮发生偏转时，油缸内所受最大油压值P=15 MPa，输出效率η=75%。因此，油缸的伸张输出力Fy1以及油缸的压缩输出力Fy2可由式(2)得出：

(2)

式中：某型汽车油缸的直径为D=50 mm，连杆直径为d=35 mm，代入可得：

油缸伸张输出力矩My1以及油缸压缩输出力矩My2可由式(3)得出：

My=FyL

(3)

式中：L为连接油缸的垂臂长度，取值L=255 mm。将Fy1和Fy2代入可得：

油缸的伸张输出力矩My1以及油缸的压缩输出力矩My2皆是转向垂臂转动的动力来源。由于在遇到阻碍物车轮发生偏转时，My1以及My2皆大于汽车在静止状态下的转向阻力矩MS，故可使转向垂臂在转向机构中正常运行。转向力矩M为：

M=My-Ms

(4)

将My1、My2以及MS分别代入式(4)可得M1和M2：

2 材料的选取

本文针对某型汽车转向垂臂常用的材料40钢、40Cr、20CrMo和TC4钛合金进行静力学分析与疲劳分析。上述材料的主要参数如表1所示。

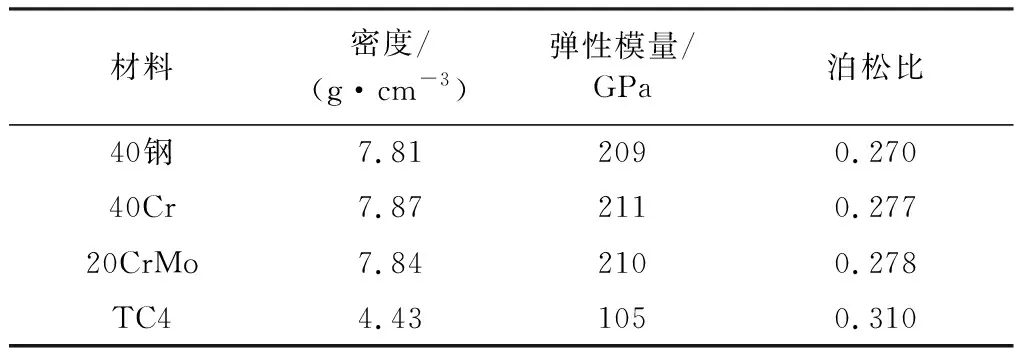
表1 转向垂臂材料的参数[10-12]

3 转向垂臂仿真过程

某型汽车转向垂臂的几何参数如表2所示。

表2 某型转向垂臂的几何参数 mm

利用三维软件Solidworks 2016对其进行建模，在不影响分析结果的前提下，对转向垂壁进行了适当简化，删除部分细微结构，如内部结构、圆角等特征。建立的转向垂臂实体模型如图1所示。

图1 转向垂臂实体模型

该实体模型建模后，保存的格式为.X_t格式，然后导入ANSYS Workbench2020中进行前处理。导入实体模型后，先设置单元类型、网格划分方式以及40钢、40Cr、20CrMo和TC4钛合金的材料参数。单元类型采用solid186单元，网格划分采用网格自适应方式，网格划分后的网格模型如图2所示，导入的4种金属材料的参数如表1所示。该模型网格划分共有49 441个单元，87 486个节点。

图2 网格自适应划分模型

4 仿真结果分析

根据某型汽车转向垂臂的实际运动和受力，对有齿轮一侧选用载荷类型为Moment(弯矩)，施加的转向力矩M可由前节公式(4)得出的计算结果选取最大值为3 349.2 N·m；另外一侧选用约束类型为Cylindrical Support(圆柱面约束)。加载位置以及受力分析如图3所示。

图3 转向垂臂的受力分析以及加载位置

4.1 静力学分析

由于40钢、20CrMo两种材料的转向垂臂分析结果相似，故下文都以40Cr和TC4为例。通过ANSYS静力学模块对某型汽车转向垂臂进行后处理求解，可获得其总形变云图以及应力云图，前者如图4所示，后者如图5所示。

图4 转向垂壁总形变云图

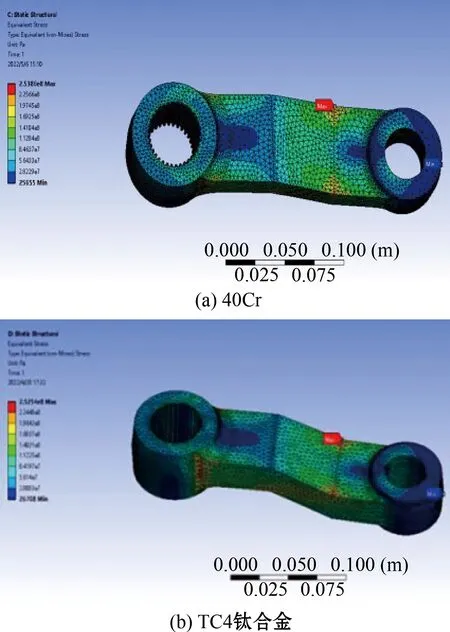
图5 转向垂臂应力云图

由图4可以看出，40Cr材料的转向垂臂最大总形变最小，表示其抗形变能力最强；由图5可以看出，转向垂臂应力云图中标记的最大值位置即为危险点的位置。经过静力学模块后处理求解，转向垂臂求解结果如表3所示，TC4钛合金的转向垂臂最大应力最小，说明其刚度最好，40Cr得转向垂臂最大总形变最小，说明其强度最好。

表3 转向垂臂的求解结果

4.2 疲劳分析

对4种金属材料的某型汽车转向垂臂进行疲劳分析。在ANSYS Workbench2020前处理中选择Engineering Data进行4种金属材料的选取和属性模块的选取，4种金属材料的数据来源于材料数据库(Engineering Data Sources)，其中包括了弹性模量、泊松比、密度以及应力-寿命(S-N) 曲线等相关数据和曲线。疲劳分析所需的4种金属材料的应力-寿命(S-N) 曲线如图6所示，横坐标为循环次数n取对数(lgn)，纵坐标为交变应力σ(MPa)取对数(lgσ)。

选用Fatigue Tool(疲劳工具)，根据转向垂臂的受力情况，选取Fully reversed(完全反转)为加载的载荷类型，考虑到转向垂臂的实际情况，疲劳系数Kf取值为0.8，采用Goodman应用修正理论来修正平均应力对疲劳结果的影响，以此得出转向垂臂疲劳敏感性曲线如图7所示。

图7 转向垂臂疲劳敏感性曲线

通过Fatigue Tool疲劳模块对转向垂臂进行后处理求解，可获得其安全系数云图以及寿命和损伤云图，前者如图8所示，后者如图9所示。

由图8可看出，TC4钛合金的某型汽车转向垂臂最小安全系数最高；由图9可看出，TC4钛合金的某型汽车转向垂臂使用寿命最长。损伤值越大表示该部位使用寿命越低，也就越容易造成疲劳损坏。

图8 转向垂壁安全系数云图

图9 转向垂臂寿命和损伤云图

5 结束语

通过三维软件对某型汽车转向垂臂进行实体建模，利用ANSYS Workbench2020的静力学模块和疲劳模块对4种金属材料的转向垂臂进行求解分析，获得其相应的应力应变、疲劳寿命、安全系数以及应力应变最大的位置和损伤最大的位置，具体结论如下：

1)40Cr材料的转向垂臂的强度最好，TC4钛合金材料的转向垂臂刚度最好。通过应力应变以及疲劳分析进行4种金属材料转向垂臂的强度、刚度、使用寿命、安全系数以及自身质量等综合比较，TC4钛合金材料的转向垂臂的综合性能优于40Cr材料的转向垂臂；

2)为了满足某型汽车转向垂臂的轻量化以及可靠性，结合有限元分析结果，可对转向垂臂的无损检测和使用性能(强度、刚度以及使用寿命等)的优化提供一定的理论参考。