基于车流特性和LSTM的长期车辆轨迹预测方案
李新,蔡英,张猛,李汶锦,范艳芳
(北京信息科技大学 计算机学院,北京 100101)
0 引言
车联网作为智能交通系统的重要组成部分可以实现车辆之间、车辆与基础设施之间通信。随着车联网的发展,依赖于车辆轨迹的应用不断增多[1],如碰撞预测、边缘计算中的数据检索、交通管理和时延容忍数据收集等,预测车辆轨迹可以使得这些应用运行更加高效。其中碰撞预测需要短时间内高精度地预测车辆未来轨迹,以提高驾驶的安全性和舒适性。时延容忍数据收集需要预测车辆较长时间的轨迹,同时相比于碰撞预测应用对精度要求较低。例如在边缘计算中通过轨迹预测实现数据检索,边缘服务器(edge server,ES)预测车辆轨迹后,将数据包发送到一个特定的位置来减小由于消息冗余导致的广播风暴的概率,实现高效检索[2]。
现有的轨迹预测方案可以分为3类[3]。一是基于物理/机动模型的方案,其方案可以在短时间内(小于1 s)准确预测,但是由于预测时间过短导致驾驶员不能及时做出反应。基于物理/机动模型的方案假定车辆有恒定的速度和方向,这与实际情况不符[4]。二是基于传统机器学习的方案,其方案可以在2~3 s内准确预测。基于传统机器学习的方案致力于离散位置预测,这实际上是一个多分类问题,并且不适合预测具有固定采样间隔的轨迹序列[5]。三是基于深度学习的方案,其方案利用不同神经网络模型的特性,充分考虑车辆历史轨迹、驾驶风格和周围车辆的行为等因素对车辆轨迹的影响,可达到较高的预测精度。采用的模型主要有卷积神经网络(convolutional neural network,CNN)、图神经网络(graph neural network,GNN)和长短期记忆(long short-term memory,LSTM)网络[6]。其中基于CNN和GNN的方案可以捕捉车辆历史轨迹中的空间特性及周围车辆的交互影响,但无法捕捉到轨迹序列中时间维度上的影响。LSTM具有“记忆”特性,在序列-序列(sequence to sequence,seq2seq)[7]的预测任务中表现出良好的性能。Zhu等[8]从理论上证明了车辆未来的轨迹与它历史的轨迹高度相关。车辆轨迹预测本质上也是seq2seq预测,因此LSTM是实现长期轨迹预测最有前景的方法。Altché等[9]首次将LSTM模型运用到车辆轨迹预测,同时考虑周围不同车辆类型的交互影响。Wang等[10]不但考虑了周围车辆的交互影响,而且将交通规则纳入方案中提升预测精度。Khakzar等[4]将车辆空间占用信息和车辆运行周围安全风险信息同时输入预测模型中。Wang等[5]将地图栅格化,针对目标车辆可以预测多个时间步的多模态状态。Park等[11]预测网格图上的占用概率,并应用集束搜索算法来选择k个最可能的轨迹。
1 预备知识
LSTM是循环神经网络的变体,可以有效克服梯度消失的问题。一个LSTM网络由多个神经元组成,每一个组成单元的结构如图1所示。LSTM神经元由遗忘门、输入门、输出门实现“记忆”功能。遗忘门控制在ct-1中保留多少信息,输入门决定ct-1中保留多少xt的信息,输出门决定ot中多少信息被输出到ht。LSTM的工作过程可由式(1)描述:
(1)


图1 一个LSTM组成单元结构
2 本文方案
针对城区场景,由于市民出行在时间上具有周期性,在目的地上具有固定性,因此城区中车流在早高峰时集中在从居民区至办公区、写字楼等,在晚高峰时车流趋势相反,因此车流受到居民出行时间、道路限制和城区规划的影响,在地理空间上具有聚集性,在时间维度上具有潮汐性。由于车流由多条车辆轨迹组成,因此针对长期车辆轨迹预测,这两种特性将有助于减少预测误差。地理空间上的聚集性即为位置,本文所提方案通过分析每个位置出现的频次,为其设置相应的权重值,用以描述位置对轨迹的影响程度。时间维度上的潮汐性指的是在不同时间段时车流趋势不同,本文所提方案中模型的输入包含了一天内多时段的历史轨迹序列,其已含有单个车辆轨迹在时间维度上的特征,无需重复进行特征工程建立单独特征。因此,本方案采用车流聚集性和潮汐性作为特征,设计了长期车辆轨迹预测方案,减小长期预测时的位置误差,提高方案的泛化性。
2.1 问题形式化描述
本方案采用由编码器和解码器组成的seq2seq架构,编码器和解码器均采用LSTM模型。编码器读取输入历史轨迹序列并将其转换为一个固定长度的矢量作为输出;解码器使用编码器的输出来初始化LSTM模型隐藏状态(ht,ct),随后在迭代过程中生成预测轨迹序列中每一时刻的位置。基于LSTM的编码器-解码器模型如图2所示,其中,Sp为预测的轨迹序列,So为观察到的历史轨迹序列,to为观察时间,tp为预测时间。

图2 基于LSTM的编码器-解码器模型
本方案的轨迹预测函数f通过上述模型学习得出,其中历史轨迹序列作为训练数据,预测轨迹序列作为标签数据。历史轨迹序列由多个时刻的车辆状态信息组成,每个时刻的车辆状态信息中包含3个特征,分别是经度、纬度和位置权重。经度、纬度用以确定车辆位置,位置权重用以描述该位置对车辆轨迹的影响程度。预测轨迹序列同样也由多个时刻的车辆状态信息组成,与历史轨迹中不同的是,预测轨迹中每个时刻的车辆空间状态信息只包括经度和纬度,用以确定车辆位置。将轨迹预测过程形式化为式(2)所示。
(2)
式中:f为预测函数;Vt为车辆在t时刻的实际车辆的状态;V′t为车辆在t时刻的预测车辆状态;(x′t,y′t)为车辆在t时刻的预测坐标。
本方案采用权重的差异性代表车辆位置的聚集性,设计每个位置的权重值代表车辆密度,权重值越高表明该位置越有可能是车辆的下一时刻位置。首先对原始数据进行清洗,去除异常数据,如车辆不活跃时段的数据、位置发生突变的数据和不属于城区范围内的数据;其次统计剩余数据中所有位置坐标出现的次数作为该位置的权重,将坐标与该坐标的权重建立一一对应关系。将上述过程形式化表达如式(3)所示:
2)喷药操作要规范,药液雾化效果要好,喷头不能离果实太近,喷药过程中如发现药液产生沉淀,不能搅拌后继续喷,因为沉淀物易堵塞喷头、刺激果面。
(3)
式中:wt为当前坐标的权重;(xt,yt)为车辆在t时刻的坐标;loc为包含所有坐标的集合;count(xt,yt)为统计函数,用以统计(xt,yt)在loc中出现的次数。
2.2 系统模型
本方案系统模型如图3所示,其中有两个实体,即车辆和ES。车辆之间、车辆与ES之间通过无线连接;ES之间通过光纤连接。车辆上的应用,通过车辆之间或车辆与ES之间共享位置,预测周围车辆的轨迹,车辆根据预测结果做出相应的驾驶行为。部署在ES上的应用,根据收集到的车辆位置和位置权重预测车辆轨迹,将预测结果发送到目标ES或车辆。
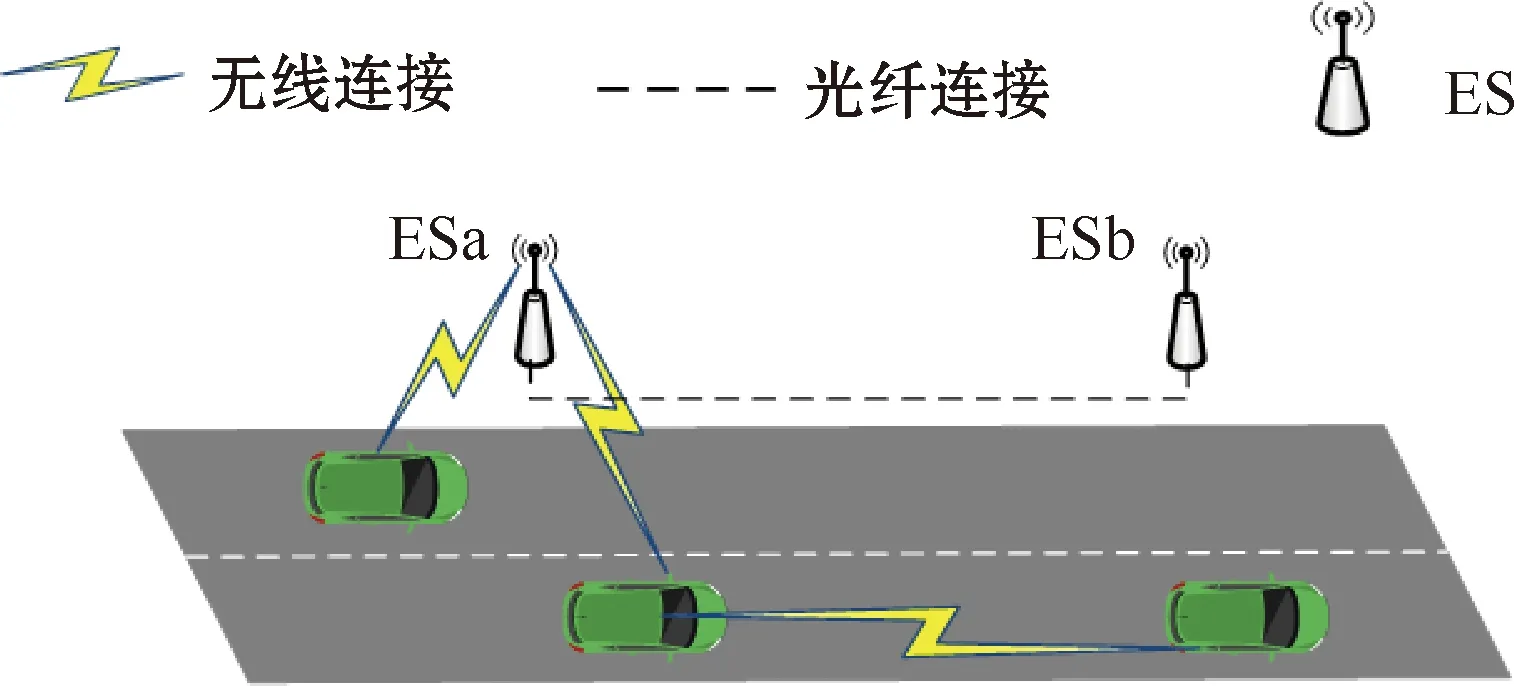
图3 系统模型
2.3 预测模型结构
本文方案的预测模型采用seq2seq架构。LSTM模型具有“记忆”特性,擅长处理时序任务,因此预测模型中编码器和解码器均采用LSTM模型。多层LSTM与单层LSTM相比,由于预测位置误差相差很小,但是训练参数量显著增加,因此在编码器和解码器中均采用一层LSTM模型。不同神经元个数的LSTM模型在测试集上的损失值如图4所示。从图中可以看出,含有120个神经元的LSTM模型在测试集上具有较小的损失值。

图4 不同神经元个数时测试集损失值的变化
预测模型结构如图5所示,其中输入是历史轨迹序列,编码器和解码器中每个LSTM模型包含120个神经元,采用带有Sigmoid激活函数的全连接层输出预测结果。
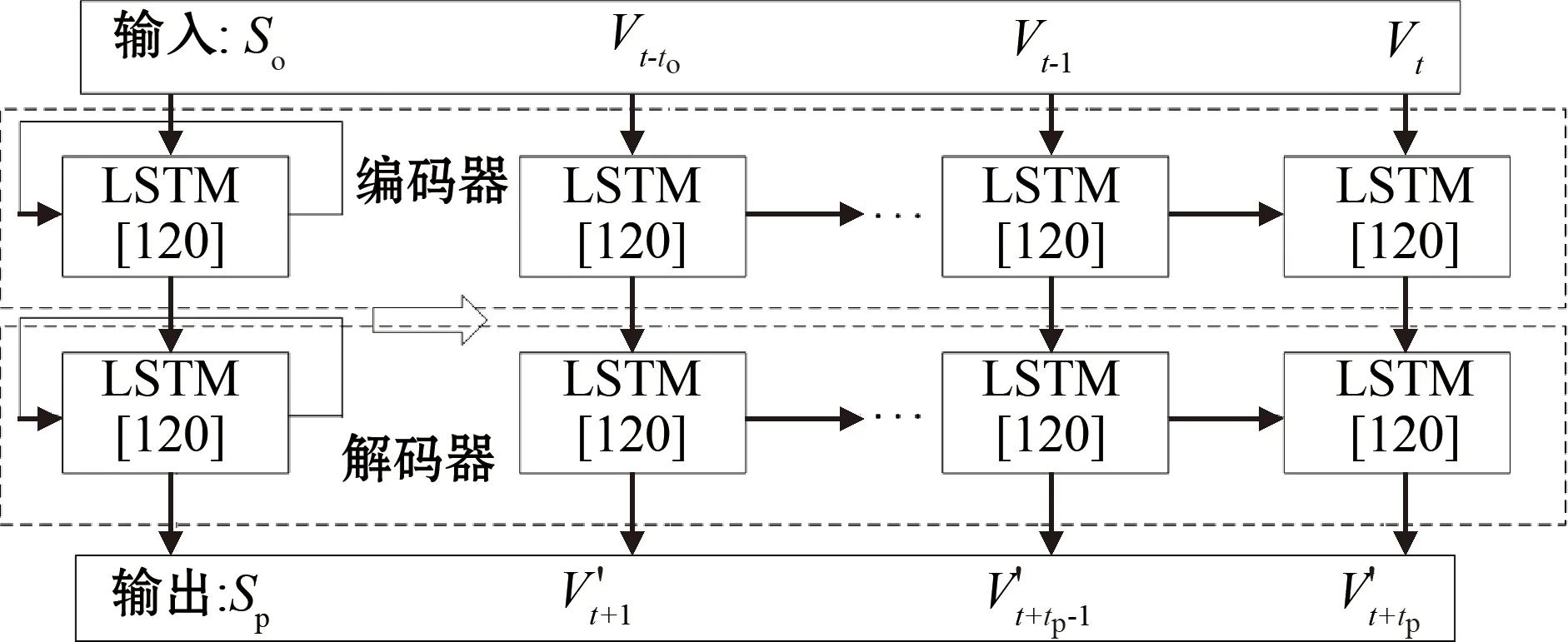
图5 预测模型结构
3 实验仿真
本实验硬件环境为Intel core i5、NVIDIA GTX 1650。软件环境为Windows 10、Python 3.6、Pycharm 2020和Tensorflow 2.5。
3.1 数据集和预处理
本实验采用的数据集为T-drive[13]。该数据集包含了2008年2月2日至2月8日期间,北京市10 357辆出租车一周的轨迹。GPS坐标的总数约为1 500万个,轨迹的总距离为900万km,平均采样间隔为177 s,平均距离约为623 m。
工作日高峰时段车流聚集于工作场所和住宅区域,休息日则是休闲娱乐场所和住宅区域。根据上述特点首先将数据集分为工作日数据集D1和休息日数据集D2两个部分。其次,考虑到2008年北京市发展状态以及人们日常出行时间,只保留北京市四环内,7∶00至21∶00的数据。最后,为验证长期预测和采样间隔较长时的效果,只保留了采样间隔为300 s的轨迹数据。本实验将3个时刻轨迹信息作为输入,预测后3个时刻的轨迹。
3.2 模型训练
本方案模型训练时采用早停的方法防治模型过拟合,即当验证集上损失值变大时,立即停止训练。因此将训练集按照8∶1∶1分为训练集、验证集和测试集。由于D1数据量远大于D2,车流聚集性在工作日更加明显,因此训练模型采用D1。相较于平均绝对误差和均方误差,均方根误差(root mean square error,RMSE)对于误差较大的预测结果更加敏感,因此损失函数选择RMSE,其值为:

(4)
由于Adam[14]优化器在多领域深度学习中均有较好的精度,因此本文优化器选择为Adam,其学习率为0.001,经过多次实验验证后,模型参数如表1所列。

表1 模型参数设置
3.3 方案评估
3.3.1 评估指标
本实验采用常规评估指标均方根误差、平均位置误差(average displacement error,ADE)和最终位置误差(final displacement error,FDE)。ADE和FDE的计算公式分别如式(5)、式(6)所示。
(5)
(6)
3.3.2 对比实验
将本文方案与不含有位置权重特征的CTAL方案(CTAL without position weight ,CTAL-W/O PW)、SU-LSTM[5]和PRB-LSTM[10]以相同的训练方法进行对比。其中CTAL-W/O PW为消融实验,采用D1测试集评估模型。平均位置误差和最终位置误差如图6所示,均方根误差如图7所示。
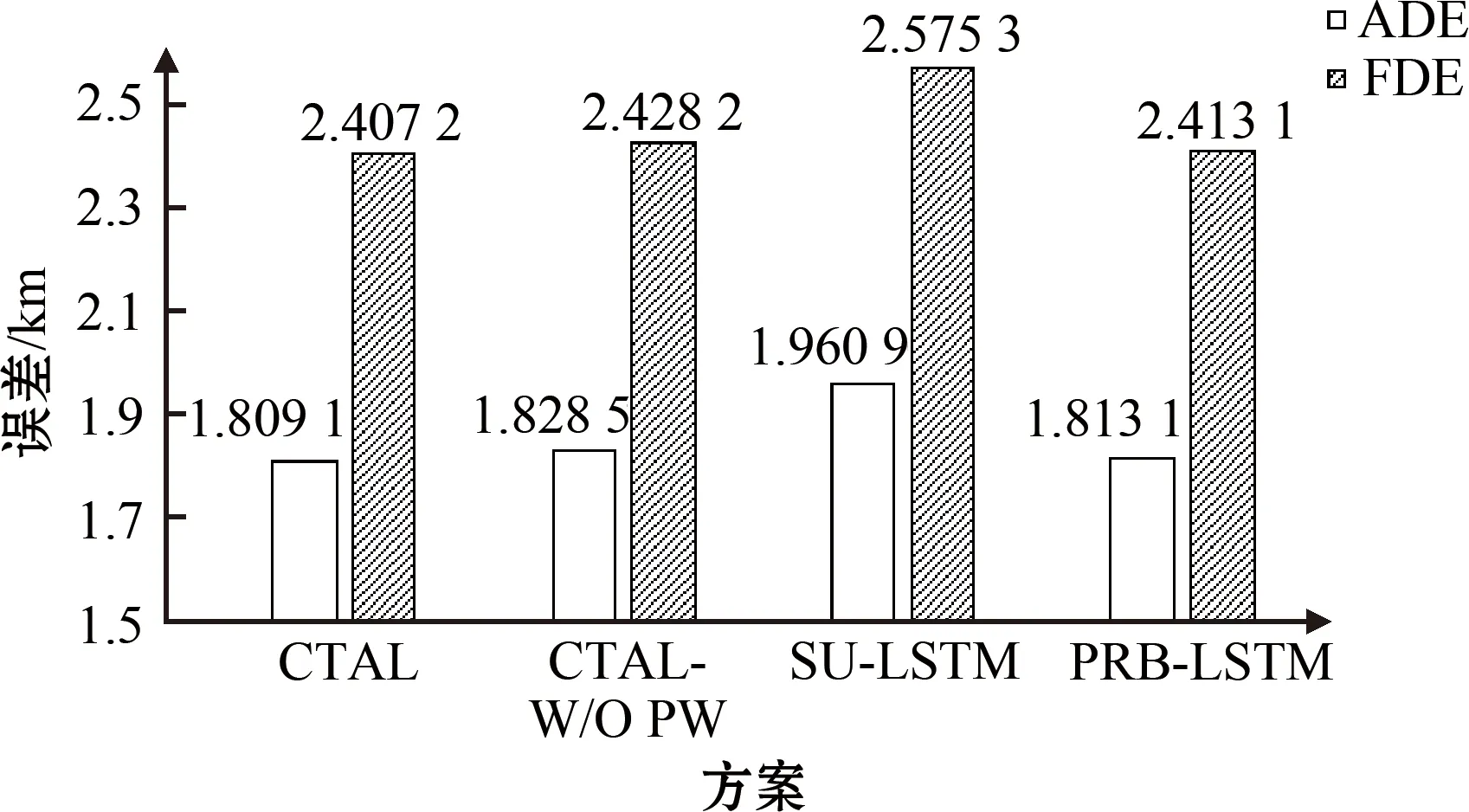
图6 D1测试集上的平均位置误差和最终位置误差

图7 D1测试集上的均方根误差
从图6、7可以看出,本文方案的平均位置误差、最终位置误差和均方根误差均优于其他3种方案。同时在D1测试集上本研究对比了各方案在300 s、600 s的平均位置误差和在900 s的最终位置误差,如表2所示。

表2 D1测试集上的预测位置误差 km
从表2也可以看出,本文方案在每个时间的平均位置误差和最终位置误差小于CTAL-W/O PW和SU-LSTM方案,PRB-LSTM方案的平均位置误差和最终位置误差与本文相近。图8所示为各个方案的神经元数量对比,从图中可以看到,本文方案和CTAL-W/O PW的模型均使用了242个神经元,而SU-LSTM使用了770个,PRB-LSTM则共计使用了642个神经元。本文所提方案训练参数数量明显少于SU-LSTM和PRB-LSTM。

图8 神经元数量对比结果
为了验证本文方案的泛化性,使用D2数据集来评估模型,实验结果如图9、图10、表3所示。从实验结果可以看出,本方案在D2上同样具有较好的实验结果,表明本文方案具有较好的泛化性。

图9 D2上的平均位置误差和最终位置误差

图10 D2上的均方根误差

表3 D2上的预测位置误差 km
4 结束语
本文针对城区场景,利用车流聚集性和潮汐性,分析不同地理位置对轨迹的影响程度,确定了位置权重以体现车辆密度,设计了基于LSTM的编码器-解码器方案实现轨迹预测。该方案输入为车辆历史轨迹,包括车辆位置和位置的权重,输出为由车辆位置组成的轨迹。在D1测试集上的实验结果表明,所提方案与消融实验方案对比,在预测时间300 s和600 s中平均位置误差分别降低了1.4%、1.1%,在预测时间900 s时的最终位置误差降低了0.9%,均方根误差降低了0.9%。在D2上的实验结果表明,所提方案与消融实验方案对比,在预测时间300 s和600 s中平均位置误差分别降低了1.3%、0.8%,在预测时间900 s时的最终位置误差降低了0.6%,均方根误差降低了1.0%,表明所提方案具有较好的泛化性。

