一般自旋系统的相位
吕小茜,于肇贤
(1.廊坊职业技术学院 机电工程系,廊坊 065000;2.北京信息科技大学 理学院,北京 100192;3.北京邮电大学 网络与交换技术国家重点实验室,北京 100876)
0 引言
Berry于1984年在量子绝热理论中发现,当依赖于参数的哈密顿量的循环演化沿着参数空间中的封闭曲线传输绝热量子态时,除了一般传统的动力学相位外,在循环演化过程中还获得了几何相位。这一发现在学术界引起了广泛关注,随着时间的不断推移,众多科研爱好者纷纷加入其中,量子系统的相位问题已然成为目前的研究热点之一。Lewis[1]提出的量子不变理论是处理具有时间相关哈密顿量系统的有力工具。Gao 在参考文献[2]中通过引入基本不变量的概念对其进行了进一步的推广,Aharonov 等[3-4]将其用于研究与时间相关的薛定谔方程相关精确解的几何相位。量子在绝热演化过程中的几何相因子和在非绝热推广中的Aharonov-Anandan 相因子也得到了许多研究者的广泛关注,它们不仅与许多重要的物理问题密切相关,而且在许多实验中也已经得到了验证。其中,Berry几何相位的发现不仅对旧的量子绝热近似理论进行了突破[4],也为我们提供了对许多物理现象的新见解。如今,Berry 相位的概念已经在一些不同的方向得到了发展[5-10],但是其方法很难推广到一般的自旋系统的相位。本文利用Lewis-Riesenfeld (L-R)不变理论引出与时间相关的薛定谔方程,通过求得精确解的方法来研究一般自旋系统的动力学相位和几何相位,并且在此基础上讨论得到了Aharonov-Anandan 相因子。
1 L-R不变理论
(1)
则此时与时间相关不变量|λn,t〉的本征值方程为
(2)

(3)

|λn,t〉s=exp[iδn(t)]|λn,t〉
(4)
这表明|λn,t〉s(n=1,2,…)形成了方程(3)的完整解集。那么薛定谔方程(3)的通解可以写成
(5)
其中

Cn=〈λn,0|ψ(0)〉s
(6)
2 动力学相位和几何相位
考虑一个具有时间依赖性的一般自旋系统,它的哈密顿量为
(7)
(8)
它们具有交换关系:
(9)
(10)
这里θ和φ由方程(1)确定并满足关系:
(11)
Bzsinθcosφ=0
(12)
Bzsinθsinφ=0
(13)
其中θ和φ上的点表示时间导数。
构造幺正变换:
(14)
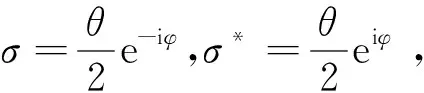
通过上述推导过程很容易得到:
(15)
(16)

(17)

(18)
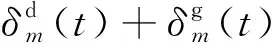
(19)
和几何相位
(20)
此时若考虑循环演化这一条件,则几何相位会变为
(21)
该结果即为 Aharonov-Anandan 相因子。
3 结束语
利用L-R不变量理论,本文研究了一般自旋系统的相位。通过利用与时间有关的薛定谔方程、幺正变换和Baker-Campbell-Hausdoff 公式等计算方法,分别求出了一般自旋系统的动力学相位和几何相位。特别是,当考虑循环演化的条件时,一般自旋系统会出现 Aharonov-Anandan 相因子。以上研究成果将对特殊自旋系统相位的研究推广到了一般自旋系统相位的研究,证明了Berry相位在一定条件下的普遍性。希望本文研究结论为其他量子系统的研究提供一些参考和借鉴。

