南芬露天铁矿边坡开挖稳定性实验研究①

彭岩岩，宋 南，刘宇航，张海江

（1.绍兴文理学院 土木工程学院，浙江 绍兴 312000；2.绍兴文理学院 浙江省岩石力学与地质灾害重点实验室，浙江 绍兴 312000；3.衢州市柯城区住房和城乡建设局，浙江 衢州 324000）

露天开采是铁矿资源的基本开采方式之一，随着开采量增加，形成了大量高陡边坡，边坡受降雨、开挖扰动、结构面等因素影响，易发生滑坡、崩塌等地质灾害，对矿区工作人员和设备安全产生较大影响。近些年来，许多学者对边坡稳定性问题进行了研究，旨在通过监测开采过程中的边坡变形情况，提前发出预警［1-10］。

本文以南芬露天铁矿为研究背景，开展大型地质力学模型实验和FLAC3D数值模拟实验，研究滑体在不同开挖阶段的变化特征以及锚索的变形情况，对比分析不同开挖方式对边坡稳定性的影响，以期对类似露天矿高陡边坡稳定性分析提供借鉴和参考。

1 工程背景

南芬露天铁矿位于辽宁省本溪市南芬区，是全国大型黑色冶金矿山，也是本钢铁矿石主要生产基地，矿区内广泛分布着4种地层且断裂构造发育较复杂，在开采中形成大量高陡边坡，易发生滑坡破坏。2011年10月5日，南芬露天铁矿298～370 m监测平台发生大规模滑坡，滑坡现场破坏特征见图1。该区域岩体主要由云母石英片岩和绿帘角闪片岩组成，其工程岩体力学参数见表1。

图1 滑坡现场破坏特征图

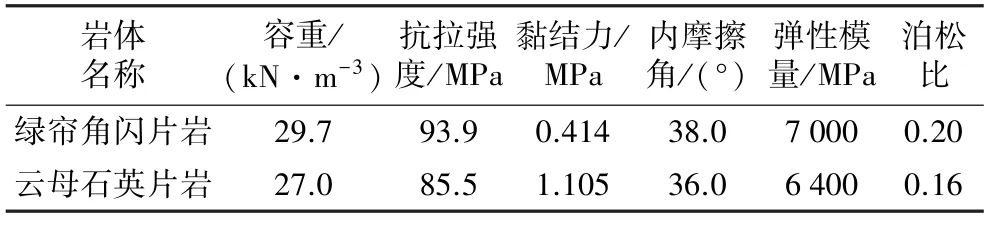
表1 工程岩体力学参数

2 地质力学模型实验

2.1 模型方案

地质力学模型实验利用深部地下工程破坏结构效应物理模型实验系统进行实验，真实还原从开挖到滑坡全过程。模型材料选取水灰比1∶1的石膏单元板作为模拟材料，石膏力学参数见表2。

表2 石膏力学参数

根据表1～2参数，计算容重相似比Cγ和应力相似比常数Cσ，其中Cγ计算式如式（1）所示：

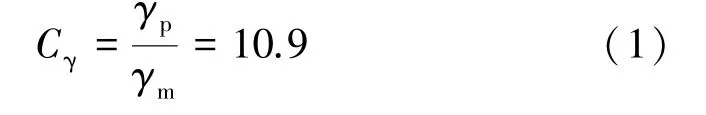
式中γp为岩石容重平均值；γm为石膏容重。根据边坡实际高度72 m和实验模型搭建高度1.6 m，计算得出几何相似比Cl＝45；根据实验机能施加的最大载荷和岩体力学参数，计算得出应力相似比Cσ＝7.8。

地质力学模型以“298～370边坡”为原型，用石膏单元板按几何相似比搭建模型尺寸长×高×宽＝1 750mm×1 600 mm×400 mm。

在地质力学模型中设置锚索，用浅色线描出，地质力学模型如图2所示。

图2 地质力学模型

2.2 实验过程

为了使地质力学模型达到真实的受力状态，实验前须对模型进行预加载，坡顶竖向荷载加载过程见表3。

表3 坡顶竖向荷载变化

坡顶预加载完成后，对边坡中区域①进行开挖。开挖共分3次完成，每次开挖36 cm，每次开挖后，需等待5 min，待模型稳定后进行下一次开挖，观察开挖过程中滑体变化情况，图3为地质力学模型开挖全过程。

图3 地质力学模型开挖全过程

模型预加载后，模型处于开挖初始阶段，单元板之间的缝隙都压密闭合，模型整体性较好，与真实边坡受力状态一致。待稳定5 min后，对开挖区进行第1次开挖，此阶段滑体部分出现纵向裂缝，锚索无明显弯曲变形。第2次开挖后，裂缝从坡顶向水平岩体扩展，锚索处滑体鼓起，有滑出趋势，锚索出现弯曲变形，且锚索上部岩体变形明显。第3次开挖后，裂缝从滑体坡顶贯通至水平岩体，锚索、局部坡顶岩体和锚索周围岩体破坏，边坡失稳破坏。

2.3 实验结果分析

实验过程中，水平岩层发生少量竖向位移，无横向位移；水平岩体与滑体之间位移差明显；滑体区域横向位移和竖向位移均发生突变；锚索约束周围岩体位移发展，影响滑体滑出位置，滑体未沿着坡脚滑出破坏而沿软弱面从锚索下部滑出。实际工程中可监测边坡坡顶位移变化。实验在无模拟降雨的情况下开挖，边坡失稳破坏，说明降雨是诱发本次滑坡的间接原因，不合理开挖是本次滑坡的主要原因。

3 数值模拟

3.1 模型建立

建立长×高×宽＝1 750 mm×1 600 mm×400 mm的边坡模型，模拟参数与石膏力学参数一致。为真实模拟锚索在开挖中变形情况，在FLAC3D中设置参数定义锚索的大变形性质，使其符合恒阻大变形锚索的拉伸性质，满足模拟需求。

3.2 数值模拟结果分析

数值模型图及露天矿边坡初始阶段开挖变化情况如图4所示。开挖前，最大主应力分层分布，坡脚部分区域出现压应力，应力最大值为1.86 MPa；随着深度增加，X方向位移增加，坡脚区域出现位移集中现象，水平位移为1.11 cm；Y方向在坡顶产生最大位移7.09 cm且沉降量随着深度增加逐渐减少。

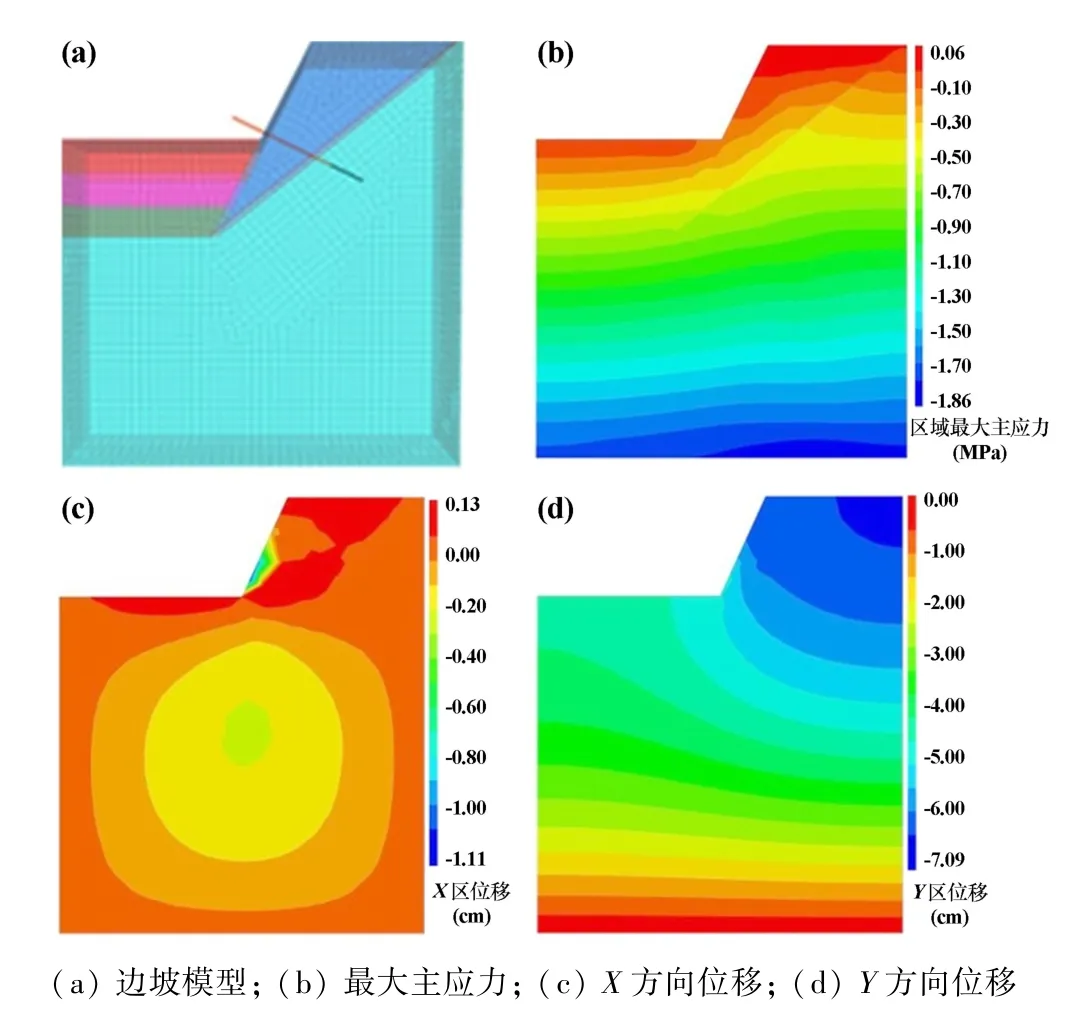
图4 开挖初始阶段最大主应力和位移

露天矿边坡第1阶段、第2阶段、第3阶段开挖变化情况分别如图5、图6、图7所示。

由图5可知，第1阶段最大主应力值1.87 MPa，X方向位移4.04 cm，Y方向沉降7.24 cm。此阶段与初始阶段相比，位移和最大主应力值均呈现增加趋势，其中X方向位移增加明显，边坡锚索附近位移梯度变化大，位移集中现象较为明显，Y方向沉降多集中在坡顶。由图6可知，开挖至第2阶段时，最大应力值降至1.85 MPa，但X方向位移增加了128%，Y方向位移增加了11.88%，且坡脚有向上运动的趋势。可能在开挖过程中，滑体产生破坏，造成应力重分布，最大应力值降低，但位移增加明显。从图7看出，随着开挖深度增加，最大应力值持续下降，位移不断增加，X方向发生17.06 cm水平位移，Y方向发生10.31 cm沉降。锚索弯曲变形发生破坏，X和Y方向分别产生22.34 cm和44.60 cm位移，锚索处Y方向向上位移趋势大于上一阶段，此阶段锚索发生严重变形和位移突变，边坡产生破坏。

图5 第1阶段开挖变形情况

图6 第2阶段开挖变形情况

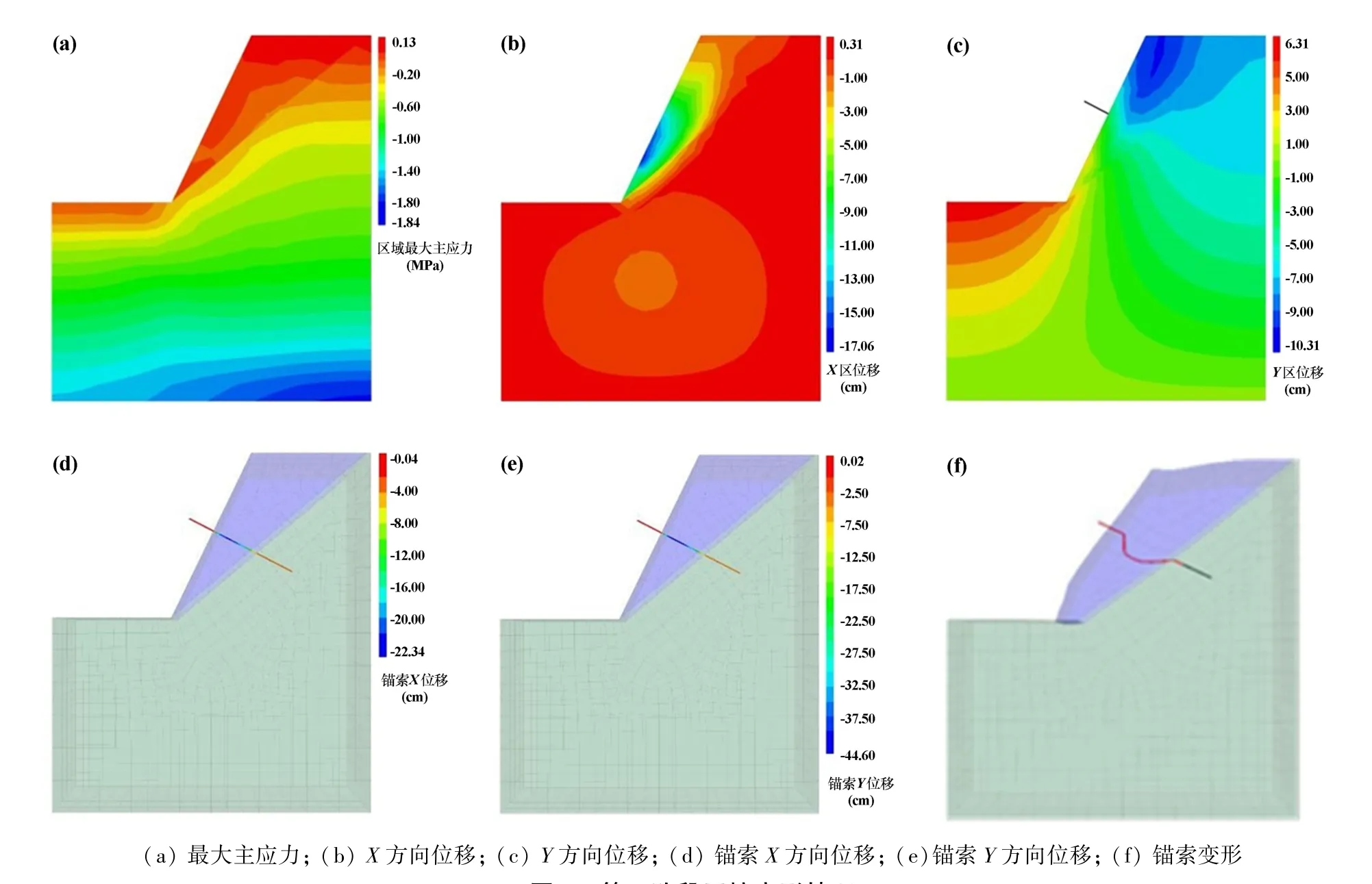
图7 第3阶段开挖变形情况

边坡模型模拟结果表明，最大主应力分层分布，在锚索处应力梯度变化较大，随着深度增加其应力也增加，且在开挖过程中应力呈现先增大后减小趋势，可能是开挖时边坡逐渐破坏、应力重分布引起。随着边坡开挖深度增加，X方向位移增大，且锚索附近位移变化集中；Y方向位移以沉降为主，大多发生在坡顶，随着开挖深度增加，沉降量明显增加，且锚索处有向上运动趋势，并随着开挖深度增加而增加。本次模拟未增加降雨条件，边坡发生破坏，故不合理开挖是本次滑坡主要原因，降雨为次要因素，与室内实验结果一致。

4 不同开挖方案数值模拟分析

4.1 强度折减与边坡安全系数

强度折减法的基本原理是将材料的黏结力C和内摩擦角φ同时除以折减系数F，得到新的C′和φ′值，通过不断增大折减系数F，计算至边坡达到临界破坏状态［11］，相对应的折减系数即为边坡安全系数Fcr。在FLAC3D中选取Mohr-Coulomb准则，基于强度折减法计算边坡安全系数，系统自行计算主应力，若主应力达到破坏准则，边破发生破坏［12］，计算所得边坡安全系数如图8所示。边坡为二级边坡，安全系数为1.25。由图8可知，分台阶开挖安全系数整体高于无台阶开挖，前10 m开挖，两种开挖方案安全系数无明显差别，开挖至15 m时，无台阶开挖安全系数低于1.25，开挖至35 m时，安全系数低于1.0，边坡已经发生破坏。分台阶开挖，安全系数始终大于1.25，边坡稳定安全，说明分台阶开挖是合理有效的。

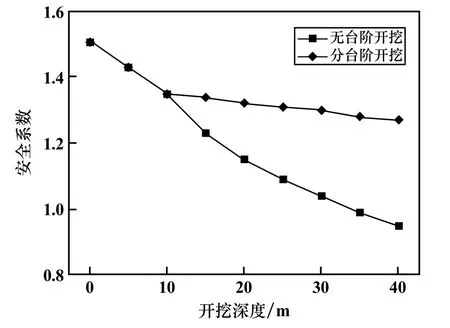
图8 安全系数随开挖深度变化情况

4.2 初始应力场

因矿区水平构造应力资料缺失，计算初始应力时只考虑重力，采用分阶段弹塑性方法计算初始应力值，结果如图9所示。可知初始应力均为负值，且应力绝对值自坡顶向坡底呈水平梯度增加。这说明开挖前模型受到的竖向应力均为岩土体在自重作用下产生的压应力，符合变化规律。

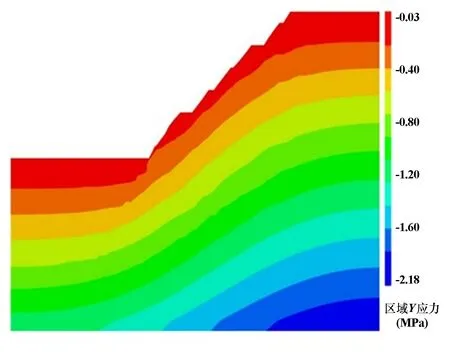
图9 初始应力场

4.3 无台阶开挖

无台阶开挖分8次开挖，每次开挖5 m，共开挖40 m。开挖过程典型主应力和位移图如图10所示。最大主应力整体分布较均匀，应力分布具有层次性，随开挖深度增加，应力逐渐增加，水平方向变化不大，边坡最大应力值为8.61 MPa，应力值增加4.7%，坡脚处水平应力集中且应力梯度变化大，且位移明显集中在坡脚附近。从位移云图中看出，位移最大值为3.55 m，位移值增加明显，在开挖30 m前位移变化不大，位移变化集中在30～40 m开挖阶段，无台阶开挖位移变化具有突变性，位移突变，边坡失稳破坏。位移与应力均在坡脚附近有明显的集中变化现象，且位移集中范围随着开挖深度增加逐渐增大，说明在开挖过程中，应力重新分布，引起应力集中范围增大，位移变化范围增大，露天矿开采时应重点加固处理这些范围。

图10 无台阶开挖最大主应力和位移

4.4 分台阶开挖

分台阶开挖时每开挖10 m，设置一个开挖平台，开挖次数与深度和无台阶开挖相同，分台阶开挖主应力和位移图如图11所示。分台阶开挖应力整体分布均匀、具有层次性，随着开挖深度增加，应力值逐渐减小，最大应力值为8.22 MPa，开挖结束后应力降低了0.36%。位移值随着开挖深度增加逐渐增加，开挖至40 m时，边坡出现最大位移值0.236 m，增加了0.04%，且边坡无应力和位移集中变化现象，边坡整体较稳定。

图11 分台阶开挖最大应力和位移

4.5 两种开挖方案对比分析

分台阶开挖位移值远小于无台阶开挖，最大位移值降低了93.35%，分台阶开挖位移变化更为均匀，没有明显的位移突变；两种开挖方案的最大应力值相差不大，但分台阶开挖最大应力呈下降趋势，降低了4.7%；在应力相同的情况下，分台阶开挖比无台阶开挖更稳定，位移变化量更小。分台阶开挖可以减轻开挖扰动对边坡的影响，更适合露天边坡开采，对于高陡边坡坡脚区域，在条件允许时，合理设置平台进行过渡，减少坡脚处应力集中现象，提高开挖过程中边坡的稳定性。

5 结 论

以南芬露天铁矿“298～370滑坡”为例，开展地质力学模型和FLAC3D数值模型，分析不同开挖阶段及不同开挖方式对边坡的应力状态和变形特性变化规律，得到以下结论：

1）基于地质力学实验和数值模拟实验，发现开挖阶段坡顶处拉应力集中，容易发生破坏，实际工程中可对边坡坡顶进行位移监测。地质力学模型实验及数值模拟实验结果与现场滑坡现象一致，验证了本次实验研究的可靠性。

2）在边坡关键位置施加预应力锚索能够很好地约束滑体位移，滑体位移的不连续性及滑坡发生时滑体沿着软弱夹层自锚索下部滑出，说明锚索能在一定程度防止滑坡发生。

3）基于数值模拟有台阶和无台阶两种开挖方案，发现合理设置开挖平台能有效减缓安全系数下降速率，并且减少坡底压力和应力集中现象，保证安全开挖，为边坡开挖方案提供实验依据。