围绕主题渐次生长：数学习题课的教学追求——以苏科版数学九（下）“二次函数”习题课教学为例

■姜国生

二次函数是九年级的重点内容，新授课之后往往要安排必要的习题课进行巩固训练，如果教师选择的习题比较零散，则不利于学生掌握同一类问题。因此，笔者围绕二次项系数为1的二次函数问题研发了一节习题课，在教研组内执教公开课后，取得较好的课堂效果，也获得组内同行的好评。下面，笔者整理本节课教学设计，并给出教学立意的阐释，供同行们研讨。

一、教学设计

1.基础热身

例1如图1，已知抛物线y=x2。

（1）在图1中，求抛物线y=x2与直线y=1的两个公共点坐标；

（2）在图1中，求抛物线y=x2与直线y=4的两个公共点之间的距离；

图1

（3）在图2中，求抛物线y=（x-1）2与直线y=4的两个公共点之间的距离；

图2

（4）在图3中，求抛物线y=-（x+2）2+2与直线y=-2的两个公共点之间的距离。

图3

［设计意图］通过上述4个题目，学生对二次项系数为1的二次函数图像的形状特征更加熟悉，为后续的变式应用奠定基础。

变式1在平面直角坐标系xOy中，二次函数y=x2+mx+n的对称轴为直线x=2，且经过点A（0，3）。将这个二次函数的图像沿y轴向下平移，请问：当向下平移几个单位时，所得到的新的函数图像与x轴的两个交点之间的距离为4。

［设计意图］有些学生先写出二次函数表达式y=x2-4x+3。教师要引导学生写成顶点式y=（x-2）2-1，让学生结合例1积累的图像特征，得到新的函数图像与x轴的两个公共点之间的距离。

2.拾级而上

例2如图4，已知正方形OBCD的三个顶点坐标分别为B（1，0）、C（1，1）、D（0，1）。试分析抛物线y=（x-h）2（h为常数）与正方形OBCD的边的公共点个数，并指出相应的h的取值范围。

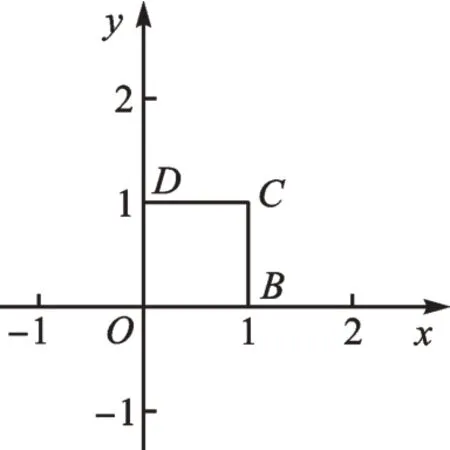
图4

［设计意图］教师通过追问的方式，引导学生自主梳理不同的临界情形对应的公共点个数，让学生明白本题的本质就是抛物线y=（x-h）2（h为常数）的顶点在x轴上平移。

变式2已知M（x1，y1）、N（x1，y1）为抛物线y=ax2（a≠0）上任意两点，其中0≤x1＜x2。若对于x2-x1=1，都 有|y1-y2|≥1，则a的 取 值 范 围 为__________。

［设计意图］变式2主要是针对例2的变式训练与学情反馈。首先，教师要引导学生学会利用“以形助数”进行分析，构造出图5。然后引导学生分情况讨论，其中包括当a＞0时，对于x2-x1=1，都有|y1-y2|≥1，所以a|x12-x22|≥1，解得a≥1。同理，当a＜0时，解得a≤-1。最后得出a≥1或a≤-1。

图5

3.拓展提升

例3在平面直角坐标系xOy中，已知抛物线y=x2-2mx+m2-1。直 线y=-x+b与x轴交于点A（3，0），与y轴交于点B，过点B作垂直于y轴的直线l交抛物线于点P、Q，若△OAP和△OAQ中有且仅有一个为钝角三角形，结合图像，求m的取值范围。

［设计意图］教师引导学生将抛物线表达式改写成顶点式y=（x-m）2-1，让学生能看出该抛物线的平移规律，求出一次函数表达式y=-x+3。此时再构造图6、图7这两种临界情形，教师鼓励学生结合图形自主分析讲解。

图6

图7

变式3如图8，已知关于x的二次函数y1=-x2-2x+n、y2=a（x-3）2-n+1（a＞0）满足对于任意的实数x，都有y1≤1+2n≤y2成立。直线y=kx-k+1（k＞0）与函数y1的图像交于A、B两点，与函数y2的图像交于C、D两点。若对于任意的k＞0，都有AB≤CD，结合函数图像，直接写出a的取值范围。

图8

［设计意图］学生可以求出n的值为-1，知道直线y=kx-k+1（k＞0）经过定点（1，1）。解决本题的关键是教师要启发学生发现两条抛物线的顶点关于点M（1，1）中心对称，引导学生结合图像观察，最终求出a的取值范围。

4.回顾小结

小结问题1：本节课继续研究的是二次项系数为1的二次函数（比如y=x2），你对这类函数的图像特征有哪些新的认识？

小结问题2：本节课的变式问题与开课时回顾的二次函数（比如y=x2）的图像特征有什么紧密的联系？可举例交流。

［设计意图］通过课后的小结问题，教师带领学生课后回顾和反思，一方面回顾本节课所学，另一方面积累本节课教学中的解题经验和策略。

二、教学反思

1.聚焦核心知识，精心选取习题

在一些重要的章节学习之后，教师会安排几个课时的习题课教学，这对于巩固新知是非常必要的。教师如果随意选取习题，缺少明确的主线或主题，则难以取得良好的教学效果，往往会出现“练过、讲过，学生还是出错”的情形。笔者认为，安排习题课首先要明确教学目标，找出教学主线，围绕教学主线精选习题。这样一节课下来，学生对这一类问题及变式题就能有着较为全面的理解，学习效果也能显著提升。

2.习题课要加强前后教学环节的关联

为了防止习题课走偏成“题海战术课”，笔者将本节课习题进行大致归类，设计成3～4个题组，每个题组是一个教学活动（或教学环节），按由易到难的顺序展开教学。每个教学环节最好有明显的关联或递进关系。例如，“基础热身”主要是带领学生复习二次项系数为1的二次函数的图像特征，而后续的“拾级而上”“拓展提升”这两个教学环节分别与第一个教学环节关联和呼应。当学生面对这些变式问题没有思路时，可以“退回”到第一个教学环节中，重新获得一些思路和启示后再挑战难题，这也是一种“以退为进”的解题策略。

3.精心预设小结问题，引导学生回顾反思

笔者发现，很多习题课教学的最后都没有课堂小结的时间。著名数学教育家波利亚说过：“习题课教学环节能促进学生对本节课所学的主题、经典图形、重要性质有一个重新审视、积累经验的作用。”如本文中的小结问题一样，教师可以围绕本节课所学，预设几个有针对性的小结问题，然后让学生在这些小结问题的引领之下学会回顾反思，促进经验分享和知识积累；还可以让学生课后继续围绕本节课训练的主线，把曾经练习过的同类习题收集、整理在一起，让学生以解题随笔或数学写作的方式梳理成文，在潜移默化中提升解题能力。