类比法在高中数学教学中的应用探究
山东省滨州市滨城区首都师范大学附属滨州中学
代海霞
著名数学家波利亚曾说:“类比似乎在一切发现中有作用,而且在某些发现中有它最大的作用.”可见,类比是数学发现和创造的一种行之有效的思维方式.事实上,类比是数学学习中常用的数学猜想方法之一,由于类比推理所得的真实性还是有待考量,需要进一步严格论证,不少教师持回避或者忽视的态度.笔者认为,类比可以将已有事物与未知事物很好地建立联系,并快速探寻到解决问题的方法,可以看作一种触类旁通的思维方式.因此教师合理应用类比教学法,不仅可以强化对一些概念、定理、公式或知识点的理解,还可以提升学生的数学学习能力.笔者拟结合教学实践谈一谈自身的一些做法,供大家参考.
1 善用类比法,促进知识系统化
大量教学实践表明,孤立的知识不易记忆且容易遗忘,而系统化、条理化的知识便于理解和掌握,更利于迁移与运用.同时,旧知识是学生探究和学习新知识的基石,教师善用类比教学法,可以很好地联系新旧知识,加强知识间的联系,展示知识的获取过程.这样,不仅可以有效避免多个本质相似的数学知识散落于学生的脑海中,还能促进知识的系统化和条理化.因此,以类比法教学让学生比较、分析相似的知识,可以使知识脉络纵横联系,同时锻炼学生抽象归纳能力.
案例1以“圆锥曲线知识”的教学为例.
在高中数学中圆锥曲线的相关知识具有较强的抽象性,知识点间独立却又相互联系.基于此,类比法教学在本单元中可以很好地实施.例如,椭圆与双曲线互相之间可以找到影子,二者定义相似度极高,仅仅是离心率的范围不同及“和”与“差”的区别,从而是类比法教学的较好素材.因此,教师可进行如下点拨:椭圆与双曲线在定义上有何不同?学生很快可以类比得出“椭圆的离心率0
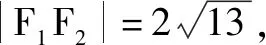
显然,通过对概念的类比和问题1的解决,不仅巩固了旧知识,使两个概念更具有识别度,还能让学生学到系统的新知识,同时一些模糊不清的知识也可以得以澄清.就这样,鼓励学生利用类比法去分析、去比较、去反思,进而揭示知识间的联系,有效梳理每一个相似的知识体系,使每个知识环环相扣,在去伪存真中让数学学习更有效.
2 善用类比法,深化概念定义
在一些概念、定义、定理等的教学中,教师可以有目的地将教材中零散的、具有联系性的、易混淆的概念或定义等有机归类,合理地利用类比法教学,揭示知识间的联系与区别,使学生在辨析中加深理解,在对比中强化记忆,以达提质增效的目的,真正体现新课程理念.当然,在具体的教学实践中,用好类比法可以促进教学,反之则会影响教学效果,更有甚者会混淆对概念或定义的理解.作为教师,在备课时需要深入研究概念是否具备类比教学法的必要性,进而巧设类比教学情境,充分激起学生的学习和探究欲望,让学生愉快地自主学习,通过类比、联系,深刻理解其本质属性,实现对知识的意义建构.
案例2以“平面向量”的单元教学起始课为例.
问题2甲车以v1=40km/h的速度行驶,乙车以v2=50km/h的速度行驶,2h后两车相距______.
生1:90km.
生2:10km.
生3:应该是不确定.
师:为什么呢?
生3:不仅需要考虑大小,还需要考虑方向.
师:谁还能列举一些既有大小又有方向的量呢?
生4:位移、速度、力……
师:位移、速度和力各自刻画的内容不同,它们有何共性呢?
生5:既有大小,又有方向.
师:很好.那有没有一种量,它只有大小,却没有方向呢?
生6:有很多,如年龄、身高、面积……
师:从数学角度来说,只有大小的量叫做数量或数.而既有大小又有方向的量则定义为向量.(抛出课题)
师:既然向量是既有大小又有方向的量,那么就需要从数与形两个角度表示向量.
问题3如下表,从表格(如表1)中的三个角度出发,该如何表示向量?又是如何想出来的呢?

表1 实数与向量对比表
生7:可以用有向线段来表示,即有起点、有方向、有长度.(教师板书)
师:一般我们用AB或者a来表示线段,那如何表示有向线段呢?(学生展开讨论)
生7:不是,二者表示的向量起点和终点不同.
…………
给出向量概念的同时回忆数量的概念,再与线段和线段长度进行类比,提供好学习的基本线索,使类比物更加清晰地呈现在学生的眼前,唤醒数学活动经验,使类比发生得自然而明确,让学生的思维不断走向深入,进而对向量的概念有清醒的认识,这样的学习效果自然是比较好的.
3 善用类比法,有效规整错题
问题是数学的心脏,学习数学必定要学会解题.而学生随着所学知识的增加,学习压力也逐步增大.那么如何回避错误解题思路的干扰,提高解题能力呢?笔者认为,以类比思想为指导归纳整理错题,可以找到数学解题的“着力点”,让学生自然认识到解题过程中的不足,锻炼数学解题能力.这样不仅可以帮助学生很好地攻克数学难题,避免出现解题的无头绪现象,还能提升对知识的理解和迁移能力,有效增添数学学习的信心.
案例3以“椭圆与双曲线”的习题练习为例.
抛物线知识是学生数学学习中的难点问题,不少学生在此处易混淆不清,导致考试时频频出错.为了改变这样的现状,笔者深入研究,整合易出错问题,设计出以下问题,让学生通过辨析,逐步厘清概念的本质属性,在真正理解新知的基础上加以灵活应用,以达到一题多练的效果.

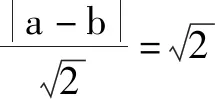
重新审视错题的过程就是不断反思和修正的过程,可以让学生客观地认识到问题,最终实现自我提升;同时这一过程对于今后的数学学习也具有较好的指导作用,可以让学生的认知在不断辨析和反思中走向深入,在不知不觉中提升学习效率.
数学能力对于数学学习的重要性是毋容置疑的,但恰当的学习方法也是提升数学学习效率的有效保障.总之,作为一种习得新知的重要方法,类比教学法对于数学教学的作用不言而喻.只不过,需要扎根于课堂的教师基于类比教学法,为学生提供具有价值的学习方法,促进知识系统化、深入化,有效规整错题,让学生的认知在类比辨析中逐步深入,提高数学学习能力.

