强化三种意识 提升复习效率
江苏省张家港市梁丰高级中学
陈庆菊
高三二轮复习是在第一轮对高中数学的基础知识等的回顾与梳理的基础上,全面开展的专题性、系统性的复习.高三二轮复习的目的就是进一步完善考生的数学知识体系与数学知识结构,并在此基础上不断总结破解数学问题的思想、意识、方法以及全面提升破解问题的能力等.合理强化数学意识,增强思想方法引导,全面深入二轮复习.结合2022年普通高等学校招生全国统一考试模拟演练(八省联考)数学试题加以实例剖析,借助强化高三二轮复习的三种意识,有效增强复习效果.
1 函数意识
例1[2022年普通高等学校招生全国统一考试模拟演练(八省联考)数学·8]已知a<5且ae5=5ea,b<4且be4=4eb,c<3且ce3=3ec,则( ).
A.c C.a 分析:利用题目条件中给出的指数关系式的恒等变形转化,根据代数式的结构特征合理构建对应的函数,强化函数意识.通过函数的构造,结合函数的求导运算以及函数的单调性确定对应的参数值的大小关系.强化函数意识,巧妙破解大小比较问题. 同理可得f(4)=f(b),0 由于函数f(x)在区间(1,+∞)上为增函数,则有f(5)>f(4)>f(3),故f(a)>f(b)>f(c). 结合函数f(x)在区间(0,1)上为减函数,所以0 故选:D. 点评:函数意识包括数学中的函数与方程的转化、构造函数、回归函数本质等函数应用意识.借助函数意识,结合函数中的代数运算,以及函数的图象与性质等相关内容,合理融入数学抽象、数学运算、直观想象等相关的核心素养,融合“函数”与“图象”加以数形结合、巧妙运算、合理转化等. 例2[2022年普通高等学校招生全国统一考试模拟演练(八省联考)数学·6](1+x)2+(1+x)3+……+(1+x)9的展开式中x2的系数是( ). A.60B.80C.84D.120 分析:利用题目条件中给出的二项展开式,巧妙借助二项式中各项的通项公式的对应规律,强化互化意识.结合等比数列的定义以及求和公式加以合理转化,根据最终和式的特征确定相关二项展开式的系数,实现本质转化,巧妙破解. 故选:D. 点评:互化意识包括数学中的定义转化、结论转化、图形转化、整体转化、变换主元、正难则反等化归与转化意识,有时还可以是不同数学知识之间的联系与转化.借助巧妙的互化意识,把陌生的、不易解决的问题转化为熟知的、易解决的问题来处理,整合数学知识,合理数学建模,改变思维角度,达到有效巧妙处理的目的. A.f(x)=f(x+π) 分析:根据题目条件中的三角函数解析式,结合三角函数的诱导公式的应用来证明关系式f(x)=f(x+π)的成立;利用三角函数关系式的恒等变换,巧妙借助三角函数的辅助角公式加以应用,结合三角函数的图象与性质来确定函数f(x)的取值范围;通过强化导数应用意识,利用函数的求导,结合导函数的符号来判断函数在给定区间上的单调性.强化导数应用意识,为破解一些与函数有关的问题提供更为广阔的空间. 故选:AD. 点评:导数应用意识包括数学中的函数与导数的关系、导数的运算、导数的几何意义、函数的单调性或极值或最值、函数图象等导数应用方面.借助导数应用意识,可以有效破解与函数有关的一些综合问题;借助导数运算,巧妙转化,合理应用,提升破解问题的效率与能力. 借助强化函数意识、互化意识、导数应用意识以及开放命题意识这三种意识,增强高三二轮复习的“灵魂”,在有效夯实“三基”(基础知识,基本方法和基本能力)的前提下,以数学思想、意识、方法为引领,真正在数学解题能力与解题技巧等方面都有所提升,形成数学综合能力.借助强化三种意识,可以有效引领并改进高三二轮复习的教学方式和方法,真正提升高三二轮复习效益,全面提升数学各方面的能力,培养数学核心素养.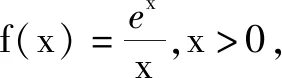
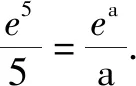
2 互化意识
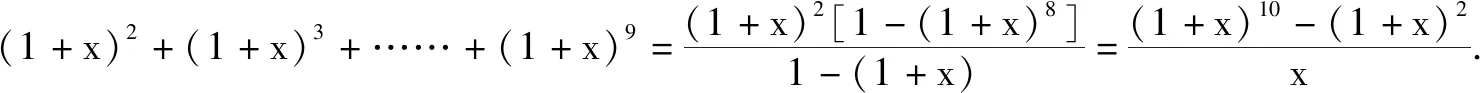
3 导数应用意识