基于数学核心素养的“等比数列前n项和”的教学
西华师范大学
曾 盼 孙 海
1 引言
《普通高中数学课程标准(2017年版)》(以下简称《标准》)要求学生在学习数学的同时也能完成数学核心素养的培养.等比数列前n项和是高中数学教材中的重点,而如何使学生获得求等比数列前n项和公式的思路是广大教师探究的重点,本文就如何在数学课堂中落实核心素养进行阐述.
2 引入环节“数学抽象”核心素养的培养
数学抽象是指不涉及事物的所有与数学无关的本质,从事物之间、事物内部的关系中抽象出一般规则,从数量及图形关系两个角度抽象出数学概念与概念之间的联系,并用数学语言来进行展示的过程,是数学的基本思想[1].
教学片段1:
师:国王要奖赏国际象棋的发明者,发明者提出,在棋盘的第一格中放1颗麦粒,在后面每格都放比前一格多一倍的麦粒,直到64格全部放满,把格子里所有的麦粒都赏给他.国王觉得这个要求很容易做到,不仅答应了这位发明者,还提出要给双倍奖赏.请问,国王可以实现他的要求吗?
学生有的赞同,有的则不然.
师:你们的理由是什么?可以把这个问题转化为数学问题吗?发明者要的麦粒数的本质是什么?
生1:我得出了1+2+22+……+263的式子.
生2:我将上式中的每一项提出来,构成等比数列{an},首项为1,公比为2.
生3:1,2,……,263就是数列{an}的1到64项,该数列的前64项的和为1+2+22+……+263.
至此,将抽象的“国王奖赏”问题转化成了数学问题.
设计意图:在引入时,教师采用故事激发学生的兴趣,引发学生思考.教师不断提出问题“可以把这个问题转化为数学问题吗?”“发明者要的麦粒数的本质是什么?”,引导学生将故事情境抽象成数学问题.
3 思路探究环节“逻辑推理”核心素养的培养
《标准》对逻辑推理是这样定义的,以一定的规则为基础,以一些事实为出发点,得到其他规律的素养[2].教师先列出1+2+22+……+263,再引导学生思考“这种算法是否适用于所有的等比数列?”
教学片段2:
师:S64=1+2+22+……+263①是一个特殊的等比数列求和,如果是n个棋盘格呢?
生1:那应该列Sn=1+2+22+……+2n-1.
师:很好.如果第一格棋盘不是放一粒,而是任意数量;后面每格不是比前格多一倍,而是多任意倍数呢?
生2:假设第一格放a1,后面每格放的麦粒数是前一格的q倍,则Sn=a1+a1q+a1q2+……+a1qn-1.
同样地,在求得等比数列前n项和公式时,也展示了逻辑推理素养.
教学片段3:
师:如何求棋盘上麦粒的总数呢?还有什么信息没用到吗?
生1:国王说要加倍奖赏,所以是2S64=2+22+23+……+263+264②.
生2:可以用②式-①式.
师:非常好,你是怎么想到的?能分享一下吗?
生2:我发现①式和②式有很多相同的项,相减就可以抵消.
学生板书:
S64=1+2+22+……262+263
①
2S64=2+22+23+……+263+264
②
②-①,得2S64-S64=264-1,所以S64=264-1.
师:数列求和的过程实际上是一个式子化简的过程.能想到在等式两边同时乘2,又发现了两个式子的特殊性,是非常不错的.264-1是一个很大的数字,那现在大家觉得国王可以实现吗?
生:不可以.
设计意图:通过探究特殊情况的等比数列求和,学生发现等比数列前n项和Sn=a1(1+q+q2+……+qn-1),其本质就是1+q+q2+……+qn-1的和,与1+2+22+……+263求和的思想方法是相同的.因此,可以采用类似的方法,推出等比数列前n项和公式.这个过程符合学生由简单到复杂的思维特点,体现了从特殊转化为一般的逻辑推理素养.在对等比数列求和公式进行推算时,很难想到在S64=1+2+22+……+263等式两边同时乘2,教师必须想办法引导学生自主产生这一种思路,所以在引入课题时,提出“国王要加倍奖赏”,这就提示学生“乘q”.学生通过观察思考出②式-①式的方法.整个过程教师一直在推动学生进行逻辑推理.
数学不仅仅是运算,同时也包含逻辑和推理.运算固然重要,但也要让学生在学习数学时思维得到提升.逻辑推理能力是人类智力五大因素之一,而且爱因斯坦提出演绎推理和归纳推理是欧几里得几何学的两大成就[2].故“逻辑推理”素养的培养是影响学生发展的重要因素.
4 公式推导和应用环节“数学运算”核心素养的培养
《标准》提出:“数学运算是以某些运算法则为依据,在确定运算对象的基础上,解决数学问题的素养.”分为如下环节:首先确定运算对象是什么,要使用的运算法则是否掌握;其次思考怎样的运算思路是恰当的,怎样的运算方法是有效的,运算过程该如何设计;最后得到运算结果等.“数据分析是根据研究对象得到数据,通过数学方法对数据进行整理、分析,达成基于研究对象知识的素养.主要包括:数据收集,数据整理,信息提取,模型建构,进行推理,得到结论.”[3]
教学片段4:
师:我们算出了特殊等比数列的和,怎么推广到一般情况呢?Sn=a1+a1q+a1q2+……+a1qn-2+a1qn-1如何化简呢?
生1:等式两边同时乘2.
生2:不对,同时乘2得到的新式子和原式相减不能抵消.
生3:应该乘q.
师:很好.我们刚刚乘2是因为每格是前一格的2倍,现在是前一格的q倍,所以应该乘q.
教师板书:
Sn=a1+a1q+a1q2+……+a1qn-2+a1qn-1
③
qSn=a1q+a1q2+a1q3+……+a1qn-1+a1qn
④
③-④,得(1-q)Sn=a1(1-qn).
师:两边同时除以(1-q)是否可以实现?
生:要看1-q是否为0.
师:所以分为q=1与q≠1两种情况,最后得出一般性公式
接下来我们来运用公式算一算,请看例题.
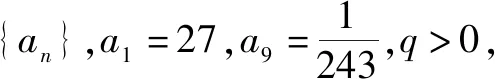
分析:此题数据看起来较难运算,且运算结果不是整数,这就需要学生在扎实的数据运算基础上建立信心.
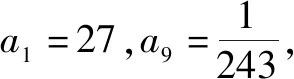
设计意图:在推出等比数列前n项和公式后,给出例题,可以让学生巩固知识并且检验自己的学习成果.
数学运算是最基础的数学能力,其他数学能力的提升必须以掌握数学运算为基础.高中数学六大核心素养中数学运算是最基本的素养.
5 解决实际问题环节“数学建模”核心素养的培养
数学建模是以实际问题为基础,通过某些方式建构数学模型,分析求解该数学模型,检验后若通过则投入使用,若不通过则重复上述环节的一个过程.
教学片段5:
师:下面来探究一道生活里的问题,请看例题.
例2某工厂本月生产了5 000 台计算机,如果每月的产量比上一个月的产量增加10 %,则从本月起,大约需要几个月可以让总产量达到30 000 台?(结果保留到个位,其中log1.11.6≈5.)
解析:由题意得,从本月开始每月的产量可以组成等比数列{an},其中首项a1=5 000,公比q=1+10%=1.1,Sn=30 000.
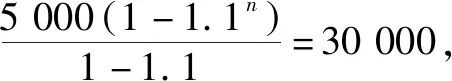
故大约5个月可以让总产量达到30 000台.
设计意图:把计算机的销售问题转化为等比数列的求和问题,在题干中提取有效运算数据把实际问题数学化,分析运算数据体现了“数学抽象”和“数学建模”素养.数学来源于生活,最终也要走向生活.高中时期用数学方法解决实际问题时,利用初等数学模型是解决问题的一种快捷方式,建立模型则是解决实际问题的关键一步[4].以生活中的实际背景进行引入的方式,激发学生的学习兴趣,也要求教师能引导学生从复杂的实际问题中舍弃干扰的信息,找到问题的核心,用数学语言展示数学问题,通过数学知识和方法建构数学模型来解决问题,最后用数学模型实现实际问题的解释.在教师的不断引导下,学生的数学建模素养慢慢提升.
6 结论
综上所述,数学核心素养的培养是一项长期且有意义的过程.数学核心素养之间相辅相成,在解决问题时通常一起渗透.同时,教师以自身为主导,以学生为主体,探究合适的教学方式,充分发挥课堂作用,增强学生的数学核心素养.

