车路协同的插电式汽车预测能量管理策略研究

陈慧勇，李 涛,，杨学青，赵治国，高建平

(1.宇通客车股份有限公司,河南 郑州 450016；2.同济大学 汽车学院,上海 201804；3.河南科技大学 车辆与交通工程学院，河南 洛阳，471003)

0 引言

随着车辆和道路基础设施互联(vehicle-to-infrastructure,V2I)和车路协同系统(cooperative vehicle and infrastructure system, CVIS)技术的快速发展，车辆可实时获取城市交通信号灯信息，规划经济车速实现生态驾驶(Eco-driving)[1]，进一步节能减排[2]。

为减少车辆在交通路口起停，文献[3]提出一种考虑信号灯切换周期的车速控制算法，运用模型预测控制(model predictive control，MPC)方法跟踪车速曲线，能使车辆免停车通过信号灯，相比基于吉普斯(Gipps)模型的跟踪方法更节油。文献[4]根据驾驶员驾驶习惯对通过交叉口的速度进行优化，从而减低油耗，缩短等待时间。上述研究虽取得较好仿真效果，但实时性与有效性未经台架或实车试验验证。

文献[5]基于车辆运动学模型，采用遗传算法和分支定界算法对连续交叉路口的通行车速进行优化，优化后辅助系统与驾驶员自由驾驶相比,节省燃油消耗达15.1%。文献[6]以油耗最小为优化目标，建立两信号灯通行最优控制问题，采用稀疏非线性优化器(sparse nonlinear optimizer, SNOPT)求解，在设定场景下可有效提升车辆经济性。文献[7]通过马尔科夫链构建红绿灯概率模型，利用A*算法求解最优通行车速，该方法可减少计算用时，且在交通信号灯密集处优势明显。但上述关于信号灯路口的研究主要针对传统内燃汽车且采用交通模型，没有考虑经济车速和新能源汽车相结合能够带来的优势和潜力。

文献[8-9]针对混合动力汽车(hybrid electric vehicle, HEV)提出一种分层控制策略，上层根据信号灯状态及车辆状态信息计算最佳通行车速，下层采用改进能量管理策略跟踪经济车速并优化整车动力源转矩分配。文献[10]针对燃料电池混合动力卡车，采用分段三角函数算法[11]对信号灯场景下的经济车速进行规划，硬件在环仿真(hardware in-the-loop, HiL)试验表明该策略能提升7%左右的能量经济性。文献[12]针对HEV提出一种基于智能交通系统(intelligent transportation system, ITS)的经济驾驶方法，通过冲击波(Shockwave)模型对车流及其排队过程进行建模，在节油8.7%的同时,以较低加速度实现了最佳的驾驶舒适性。文献[13]针对纯电动汽车提出了一种基于最优控制的经济性驾驶车速优化策略，仿真实验表明该策略相较于加速-匀速-制动策略可实现9.2%的能量节省。文献[14-15]针对插电式混合动力汽车(plug-in hybrid electric vehicle, PHEV)提出了 ecological adaptive cruise controller(ECO-ACC)双层控制器，上层控制器根据历史交通信号灯信息，利用动态规划求解全局经济车速曲线，下层控制器在保证安全的前提下跟随经济车速曲线，HiL试验表明该控制器具有较好的节油效果。上述基于经济车速规划的能量管理策略主要使用传统经济车速规划算法，利用智能优化算法对信号灯场景进行经济车速规划的较少，且未与插电式混合动力汽车能量管理策略相结合。

本文以某P2构型PHEV为研究对象，针对市区信号灯路口场景，运用动态规划及高斯(Gauss)伪普法优化求解经济车速。提出了基于 MPC的PHEV能量优化管理策略，其采用迪杰斯特拉(Dijkstra)算法求解最优转矩分配，并搭建了驾驶员在环硬件仿真试验平台，验证了所提出的经济车速规划和预测优化能量管理策略的有效性。

1 PHEV动力系统构型

本文以某款P2构型的PHEV作为研究对象。该PHEV混合动力系统主要包含发动机、驱动电机、动力电池以及6速自动变速器(6-speed automatic transmisson，6AT)等部件。该PHEV为发动机前置的后驱车型，发动机输出轴与封装的6速自动变速箱相连。整体为单轴并联的P2构型。值得注意的是，该混动6速变速箱在驱动电机前端安装了1个离合器，取消了液力变矩器，构成了1款混合动力专用变速箱。其主要技术参数见表1。

表1 某款P2构型的PHEV主要技术参数

2 市区信号灯路口经济车速规划

2.1 信号灯场景预分析

图1 车辆到达信号灯路口不同场景示意图

在不考虑前车遮挡情况下，车辆行驶至信号灯所需时间如下：

(1)

(2)

其中：d0为车辆与信号灯距离，m；v0为当前车速，m/s；tcr为车辆以v0行驶至信号灯所需时间，s；amax为车辆最大加速度，m/s2；tear为车辆以当前路段道路限速vlimit行驶至信号灯所需时间，s，即当前所需最短时间。

车辆通过信号灯可分为以下3种场景讨论：

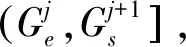
2.2 PHEV能耗模型建立

车辆的实际行驶工况直接决定了车辆的功率需求，进而对车辆的油耗产生影响，车辆行驶时的需求功率Pwheels计算如式(3)所示。基于车辆需求功率与能耗的关系，本文基于车辆微观油耗及排放模型(virginia tech microscopic, VT-Micro)[16-17]，将PHEV的瞬时能耗(energy consumption, EC)用多项式拟合的方式与v,v3,v·a相联系，瞬时能耗EC计算如式(4)所示。

(3)

(4)

其中：m为车辆额定负载，kg；g为重力加速度，m/s2；θ为道路坡度角，rad；Cd为为空气阻力因数;A为车辆迎风面积，m2；δ为车辆的旋转质量换算因数；v为车辆速度，m/s；a为车辆加速度，m/s2；b0为常数项；b1,b2,b3为多项式系数。

基于PHEV实车转鼓试验数据，采用多项式拟合得到插电式混合动力汽车电量消耗(charging of depleting, CD)和电量保持(charging of sustaining, CS)阶段的能耗模型。CD/CS阶段PHEV能耗模型系数如表2所示。

表2 CD/CS阶段PHEV能耗模型系数

2.3 经济车速规划

将车辆通过信号灯路口场景的经济车速规划问题转换为最优控制问题，选取x(t)=[x1(t),x2(t)]T=[s(t),v(t)]T作为状态变量，u(t)=[a(t)]为控制变量[4]。状态方程如下：

(5)

其中：s(t)为t时刻距信号灯的距离，m；v(t)为t时刻车辆的行驶车速，m/s；a(t)为t时刻车辆的行驶加速度，m/s2。

综合考虑经济性与驾驶员舒适性，选取目标函数为：

L(v(t),u(t))=ω1EC(v(t),a(t))+ω2a2(t)，

(6)

其中：ω1,ω2为权重系数，分别为车辆经济性以及舒适性在代价函数中所占权重。

绿灯通行约束：

(7)

速度约束：

vmin≤v(t)≤vlimit。

(8)

加速度约束：

(9)

其中：amax、amin分别为最大及最小加速度，m/s2；vlimit为当前道路限速，m/s；vmin为道路通畅时允许的最小通行速度，m/s；L为通行路段长度，m；t0、tf分别为初始、终止时间，s。

分别采用动态规划(dynamic programming, DP)算法[18]和高斯伪谱法[19]对上述最优控制问题进行求解，得到车辆在市区信号灯路口下的经济车速，具体规划结果见4.1小节。

3 基于模型预测控制的PHEV能量管理策略

基于MPC的PHEV能量管理策略流程如图2所示。首先将连续时间离散化，设当前时刻为k，控制变量为发动机转矩；之后，基于PHEV经济车速规划的结果，对需求转矩进行预测；其次，计算得到预测时域Np内的预测需求转矩序列；进而以等效燃油消耗最小为目标，利用Dijkstra算法求解出最优控制序列[20]；最后，选取最优控制序列第1个控制量，即当前发动机转矩，计算对应的电机转矩，作用于车辆模型。

图2 基于MPC的PHEV能量管理策略流程图

Dijkstra算法用于解决MPC中目标函数最优问题，其所得优化结果作为发动机转矩，用于发动机与电机的转矩分配，以减少PHEV综合等效燃油消耗，达到提升能量经济性的目的。

3.1 MPC的建立

3.1.1 预测模型

基于所规划的经济车速曲线，建立如式(10)所示的转矩预测模型，得到每一步预测的需求转矩，其中计算所需信息均可从ITS模拟器中获取。

(10)

其中：Tprdt(t)为t时刻的预测转矩，N·m；α(t)为t时刻的道路坡道角，rad；i0为主减速器传动比；ηPT为传动系效率。

3.1.2 目标函数

PHEV综合油耗由燃油消耗和电能等效油耗组成，如式(11)所示：

(11)

根据能量流动关系：

(12)

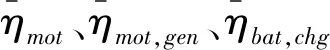
3.1.3 最优控制问题建立

选取系统控制变量为发动机转矩u(t)=[Teng(t)],系统状态变量为x(t)=[SOC(t)]。当前时刻为t=k，以PHEV在预测时域Np内的综合油耗作为MPC优化目标J。

(13)

发动机转矩为控制变量：

(14)

约束条件为：

(15)

其中：Treq(k)、Teng(k)、Tmot(k)分别为k时刻总的需求转矩、以及发动机和电机需求转矩，N·m；neng(k)、nmot(k)分别为k时刻发动机和电机转速,r/min；neng,max、nmot,max分别为发动机和电机最大转速，r/min；Teng,max(neng)、Tmot,max(nmot)分别为发动机和电机在当前转速下能够提供的最大转矩，N·m；SOCmax、SOCmin为SOC允许变化范围。计算PHEV等效综合百公里油耗时，1 kWh的电将等效为0.196 L的汽油[21]。

3.2 Dijkstra优化算法

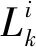
利用Dijkstra算法对PHEV动力源转矩进行优化分配，预测时域Np内的预测需求转矩序列为：

(16)

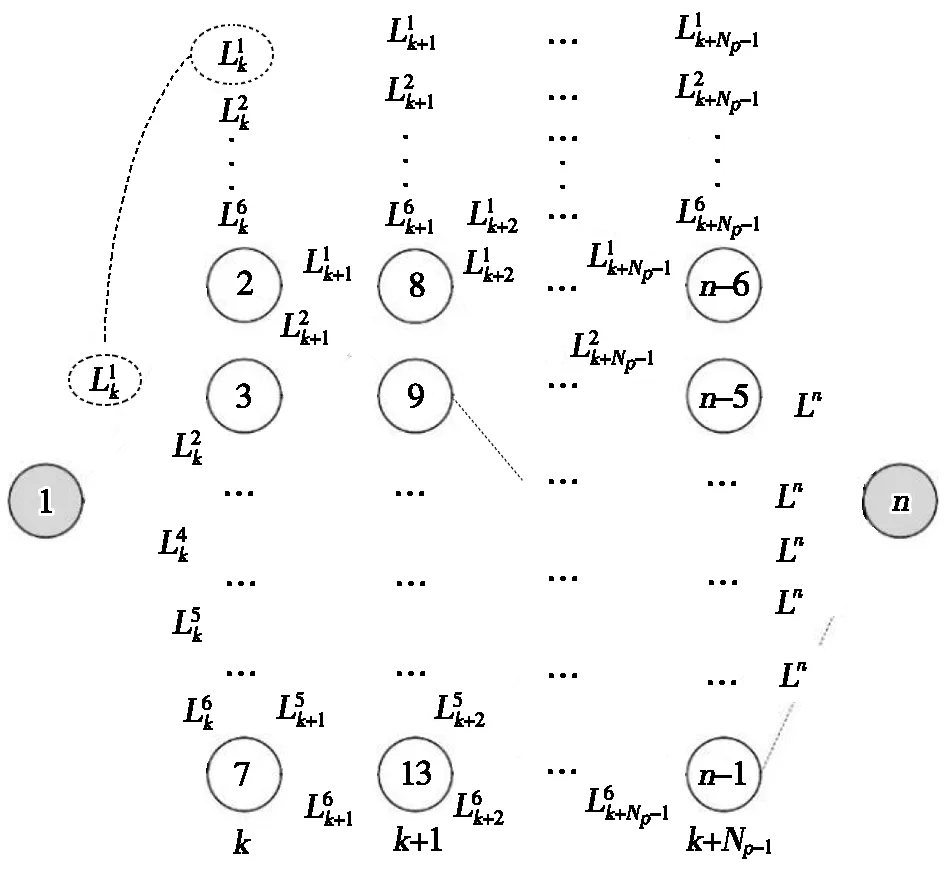
图3 Dijkstra算法求解优化目标示意图

4 台架试验

4.1 经济车速规划仿真分析

信号灯路口通行测试场景参数如表3所示，假设车辆在d0时的到达时间t0= 5 s，分别采用基于规则的分段三角函数[11]、动态规划以及高斯伪谱法进行PHEV经济车速规划，结果如图4所示。

表3 信号灯路口通行测试场景参数

(a) 经济车速曲线 (b) 等效油耗 (c) 目标函数代价

由图4a可知：3种算法所规划的经济车速具有一定的相似性，均为加速至某一车速后，维持匀速直至通过信号灯路口。相比于基于规则的分段三角函数经济车速规划而言，在等效油耗方面(见图4b)，动态规划算法和高斯伪谱法分别降低了6.31%和7.03%；在目标函数代价方面(见图4c)，分别降低了5.33%和6.40%，即2种优化算法均能有效提升车辆通行信号灯路口的经济性和驾驶舒适性。总体来看，高斯伪谱法规划的经济车速曲线较为平滑，对车辆经济性的提升在该场景下最好；动态规划算法的优化效果略低，是因为求解时的状态及时间离散点的选取对优化效果造成的影响。

4.2 能量管理策略仿真分析

基于真实道路地图信息，利用高斯伪谱法构建市区信号灯路口工况，并将该工况作为PHEV仿真模型的输入，对所提出的策略进行验证。如图5所示，选取同济大学嘉定校区外某公共主干道路的一部分作为试验场景，总长3.6 km，并提取沿途6个信号灯路口位置信息。

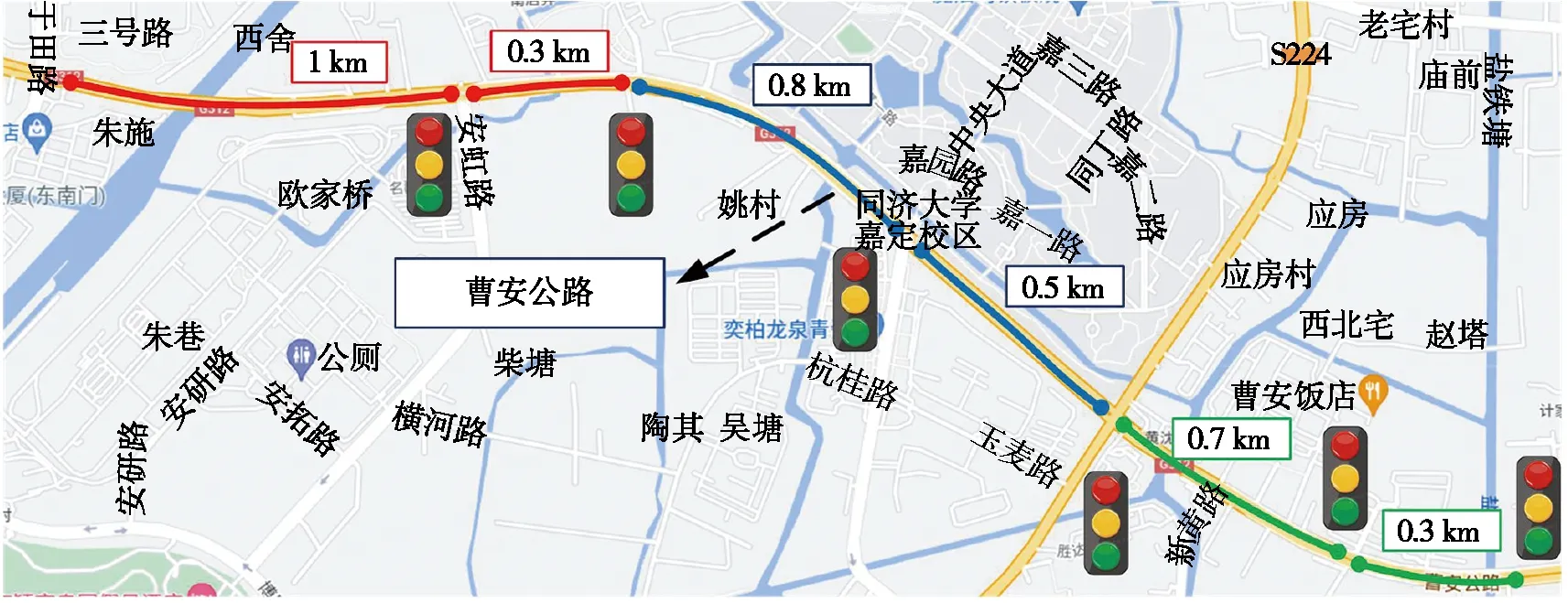
图5 市区信号灯路口工况路线图

根据上述市区连续信号灯路口工况，采用基于高斯伪谱法的经济车速规划算法。将上述6个信号灯路口分为3个路段分别进行经济车速规划，构造出市区连续信号灯路口经济车速，如图6所示。其涉及的信号灯通行场景包含加速-加速、减速-加速、加速-减速场景，涵盖了日常驾驶中经常遇到的通行情况。车辆初始速度为ν0，行驶至每个路段第一个信号灯前d0距离时开始规划连续2个路口通行的信号灯经济车速。值得注意的是，当车辆行驶至经济车速规划范围内时，算法会输出连续通行2个路口的经济车速，如图6中第1路段72～107 s所示，当车辆顺利行驶过信号灯路口后，会恢复到规划之前的初始车速ν0。由于所提出的策略只涉及信号灯通行前经济车速的规划，且因顺利通过路口后无时间等约束限制，所以不同的驾驶员在通过信号灯后会以不同的方式减速到初始车速ν0。因此，采用基于规则的分段三角函数算法规划由通过路口至返回交通流速段的车辆速度，如图6中107～120 s所示。

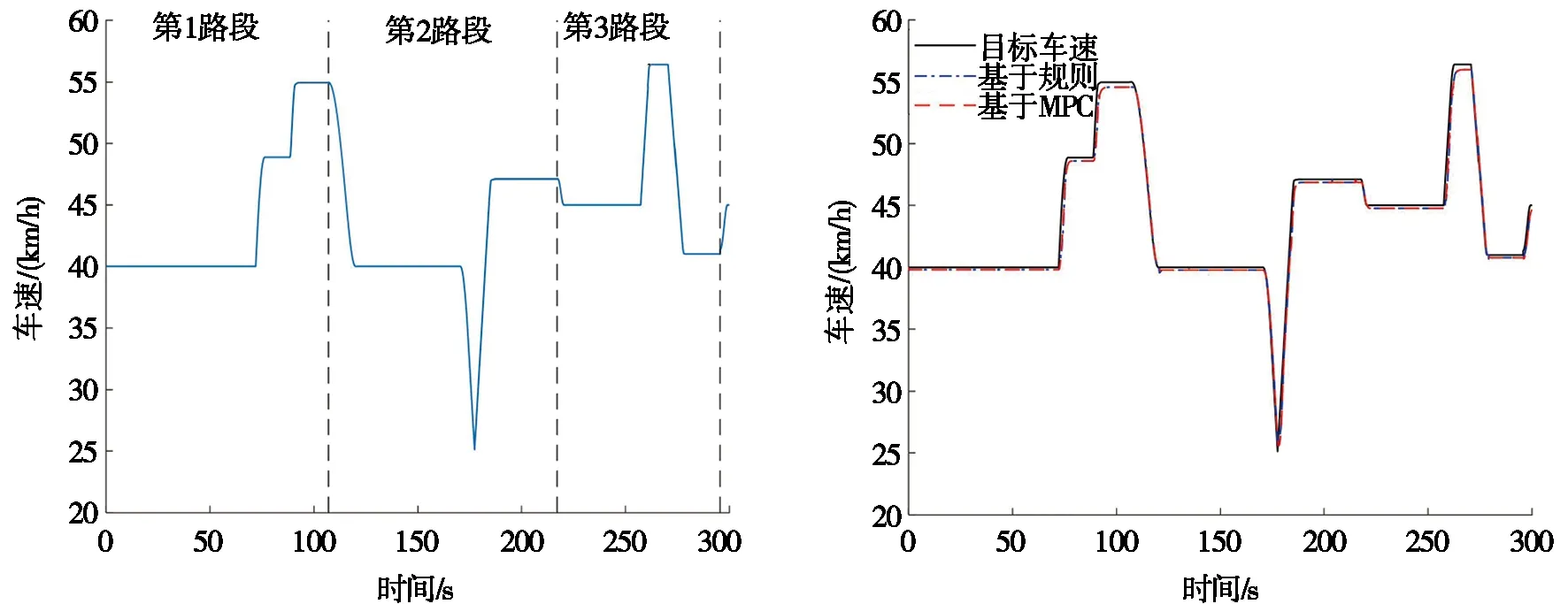
图6 构造的市区连续信号灯路口经济车速 图7 PHEV行驶车速

采用上述构造的市区信号灯路口工况对PHEV能量管理策略进行验证。使PHEV行驶在CS模式，设置初始SOC为30%，分别对PHEV基于规则的以及基于MPC优化的能量管理策略进行仿真验证，行驶车速跟踪结果如图7所示，SOC终值、发动机油耗、综合油耗如表4所示。

表4 市区连续信号灯路口工况下能耗结果

从图7中可以看出：2种能量管理策略均能较好地跟踪所规划的经济车速曲线。表4为2种能量管理策略在市区连续信号灯路口工况下的能耗结果，在基于规则的能量管理策略下，PHEV的综合等效百公里油耗为7.599 L/100 km，SOC终值为29.84%；在基于MPC优化能量管理策略下的综合油耗为7.082 L/100 km，SOC终值为29.35%。结果表明：SOC变化维持在初始值1%内，基于MPC优化控制策略的车辆能量经济性相比基于规则能量管理策略的提升了6.80%。

4.3 台架试验验证

4.3.1 驾驶员在环硬件仿真试验平台

将驾驶模拟器和PHEV动力总成对拖台架集成，构建驾驶员在环硬件仿真试验平台，以验证信号灯路口的经济车速规划算法以及MPC优化后能量管理策略。驾驶员在环硬件仿真试验平台如图8。MicroAutoBox作为实时控制器，九州华海U2控制器作为台架控制器，在Prescan仿真软件中搭建市区道路及信号灯场景。MicroAutoBox的模拟数字转换器(analog to digital converter，ADC)模块接收到踏板的模拟量信号，将其转换成数字量信号并根据驾驶员需求得到驾驶员需求转矩。MicroAutoBox中的PHEV能量管理策略根据相关信号决策PHEV工作模式以及转矩分配，并通过控制器局域网络(controller area network,CAN)总线将工作模式、挡位决策以及目标转矩等控制信号发送给台架电子控制单元(electronic control unit, ECU)。台架ECU对驱动电机、负载电机以及变速箱等动力部件进行控制，台架反馈信号通过CAN总线发送给MicroAutoBox。Prescan接收到车辆的状态信息，并集成到模拟驾驶场景中。驾驶员根据Prescan反馈的车辆真实车速以及目标车速曲线，操控踏板开度，形成闭环。

图8 驾驶员在环硬件仿真试验平台

4.3.2 台架试验结果分析

在上述市区连续信号灯路口工况下，通过台架试验验证基于高斯伪谱法的经济车速规划算法以及所提出的PHEV能量优化管理策略。与仿真设置相同，使PHEV行驶在CS模式，设置初始SOC为30%。驾驶员操作加速或减速踏板以跟踪屏幕所示的目标车速，硬件在环仿真试验结果如图9～图13所示。

图9 PHEV行驶车速 图10 PHEV等效综合能耗 图11 蓄电池SOC

PHEV行驶车速如图9所示，由于驾驶员真实地在操作踏板以跟踪目标车速，所以存在车速跟踪误差及车速波动，车速均方根误差分别为1.03 km/h(基于规则)、1.24 km/h(基于MPC)，满足跟踪目标车速的要求。图10、图11分别为2种能量管理策略在市区联系信号灯路口工况下的等效综合油耗和蓄电池SOC变化曲线。通过图10和图11可得：PHEV采用基于规则的能量管理策略行驶完整个市区连续信号灯路口工况的综合等效油耗为7.697 L/100 km，终止SOC值为29.87%；采用基于MPC优化控制策略所消耗的等效综合油耗7.314 L/100 km，终止SOC值为29.75%。2种能量管理策略的SOC偏差控制在0.5%以内，基于MPC的PHEV优化管理策略相比于基于规则的能量管理策略提升了4.98%的能量经济性。

采用2种能量管理策略的总需求转矩、发动机转矩以及电机转矩如图12和图13所示，基于规则的能量管理策略发动机峰值转矩为200.8 N·m，而基于MPC的能量管理策略发动机峰值转矩为171 N·m。基于MPC的能量管理策略与基于规则的能量管理策略相比发动机峰值转矩降低了14.84%，可以使发动机更多工作在高效区域，使得PHEV能量经济性有所提升。

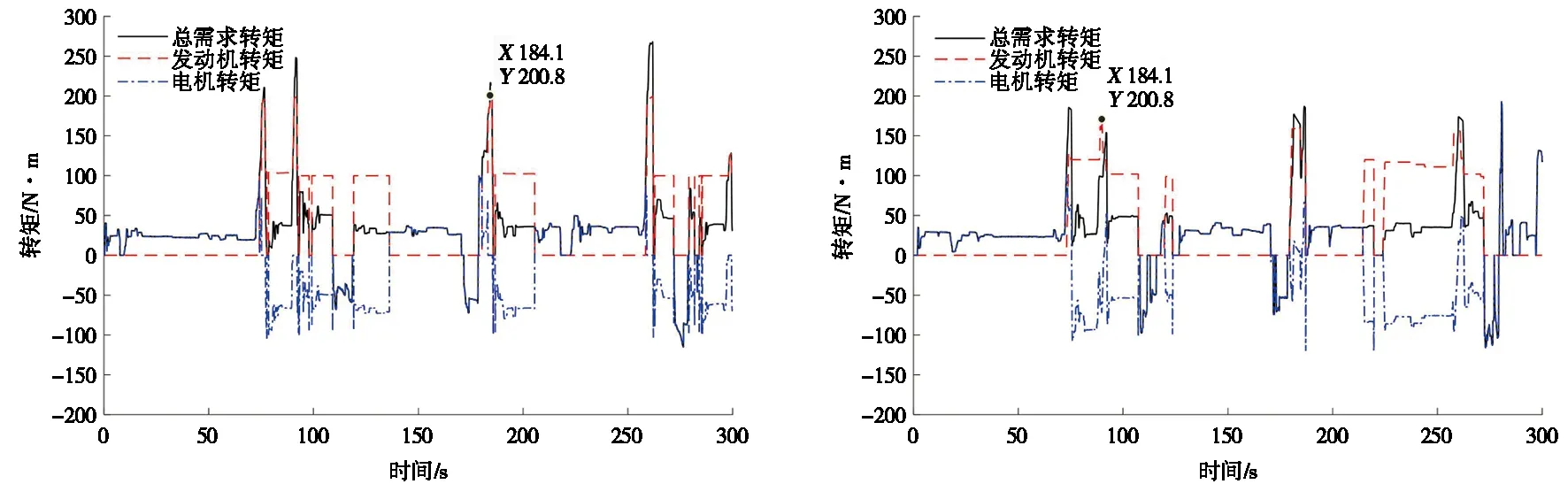
图12 基于规则的能量管理策略 图13 基于MPC的能量管理策略

在相同的策略下，与仿真试验结果相比，驾驶员硬件在环台架试验的等效综合百公里油耗分别相差1.29%(基于规则)，3.28%(基于MPC)，表明了所提出策略实际应用的有效性。此外，本文所提出的策略已实现在实时控制器中运行，也验证了所提出策略的实时性。

5 结束语

(1)以P2构型的PHEV为研究对象，对信号灯路口进行场景分析，提出了基于DP和基于高斯伪谱法的经济车速规划方法。相比于基于规则的分段三角函数方法，2者分别可降低6.31%及7.03%的等效综合油耗。

(2)将已规划的经济车速引入PHEV的能量管理策略中，采用Dijkstra最短路径算法求解预测时域内的最优发动机转矩序列。通过真实城市道路信息构建由6个信号灯路口组成的市区连续信号灯路口工况，并经过仿真和台架试验对所提出PHEV模型预测能量优化控制策略进行了验证。相比于基于规则的PHEV控制策略，基于MPC的优化控制策略在上述工况下可提升4.98%的经济性，证明了所提出的控制策略的有效性及应用潜力。

本文尚存在一些问题有待进一步研究与改进。一方面，信号灯路口经济车速规划时未考虑前方有车辆阻挡、车队一起通行路口等情况；另一方面，由于资源的限制，台架试验时信号灯信息等由实时控制器当中的模拟交通模块发出，未考虑信号解析以及通信延迟等情况。在后续研究中，可以基于V2X通信，利用地图传感器等采集道路及信号灯信息，并通过样车在真实道路上进行试验，对算法进行进一步验证和完善。