培养学生的关键能力，夯实学生的核心素养

浙江杭州市滨江实验小学（310000） 王国才

余文森教授在《核心素养导向的课堂教学》中将关键能力分为阅读能力（输入）、思考能力（加工）和表达能力（输出），这三种能力是数学学习中的基本能力。王永春在《小学数学核心素养教学论》中指出，数学思想是核心素养的核心和内涵，关键能力是核心素养的外在表现。素养与能力是紧密相连的，数学阅读能力、思考能力、表达能力直指数学的核心素养。那么如何培养学生的关键能力，夯实学生的核心素养？笔者结合实际教学谈谈自己的看法。

一、厚植阅读能力，夯实素养根基

苏霍莫林斯基说：“学会学习，首先要学会阅读。”阅读是一个人获取信息和知识的重要方式。学生根据自己的已有知识和经验，通过阅读数学素材，获取数学概念和方法，是学生主动获取有用信息、汲取数学知识、发展数学思维、理解数学语言的重要途径。数学阅读不同于一般的阅读。学生在阅读数学问题时，不能忽略任何一个字，而是要认真研读并理解它，透过文字探求问题蕴含的信息，并对信息进行加工，形成完整的认知。数学阅读能力是数学思维的基础，是学习之根。

1.去粗取精，读懂信息

审题是解题的前提，学生做错题，有时候不是真的不会做，而是因为没有养成良好的阅读习惯，不会审题，读不懂信息，因此直接影响解题效果。

例如，应用题：某建设工地为了腾出用地，把长180米、宽41米，总质量为3.6万吨的建筑整体平移290米，如果每天平移18米，17天能完成平移吗？

该题蕴含较多信息，常常有学生不会审题，读不懂信息，因此做题时无从下手。鉴于此，教师可以先让学生认真阅读题目，逐字逐句地推敲，再让学生删掉无价值的信息，一一列举出与问题紧密相连的信息：（1）每天平移18米；（2）17天能平移290米吗？删去了无关的信息：长180米、宽41米，总质量为3.6万吨。

比较精简之后的题目和原题，学生从中明白了：解答应用题要认真读题，删掉无用的信息，留下有用的信息，去粗取精，更容易理解和思考。

2.由表及里，读出联系

郑毓信教授说：“数学知识的教学不应求全，而应求联。”有些学生做错题的原因不一定是粗心、不会，而是不理解题意，找不出信息之间的联系。

例如，计算题：有10朵红花，红花比黄花少2朵，黄花有几朵？

常常有学生见“少”就减，见“多”就加。对此，教师首先应引导学生圈出“红花”和“黄花”两个词，然后在“红花”处标上“少”，“黄花”处标上“多”，再利用图示分析数量关系。

数学阅读有时要结合文字、图形、符号、表格等进行整体性阅读，由表及里找出信息间的联系。如果把题目看成外衣，阅读就是一把剪刀，思维是裁剪的方法，数字、符号、文本、图示则是衣服上的线。

3.由此及彼，读透思想

通过数学阅读，学生不仅了解数学知识，掌握数学方法，而且能感受数学的作用，理解数学思想。

例如，人教版教材五年级上册《九章算术》中的“方田章”和“出入相补法”论述了平面图形面积的算法都渗透了什么样的数学思想。学生带着“平行四边形的面积公式推导”这一问题去阅读教材内容，读出了自己的体会，在感悟中发现：计算平行四边形面积的过程蕴含转化思想。

阅读能力是数学学习之根，厚植数学阅读能力，在阅读中去粗取精、由表及里、由此及彼，把粗浅的认识深刻化，把零散的信息系统化，从而准确揭示事物的本质和规律。

二、发展思考能力，搭建素养框架

《义务教育数学课程标准（2022年版）》中提出，用数学的思维思考现实世界，通过数学思维，形成有理有据、遵循逻辑的思维品质，培养严谨的科学态度与可贵的理性精神。数学教学并不只是讲授知识，还要关注学生的思考过程，培养学生的思考习惯，让学生学会思考，发展数学思考能力。

1.因需而生，原点启思

无论是新授课教学还是复习课教学，都离不开学生已有的知识和经验。教师要了解学生的学习现状，把握教学起点，因需而生，原点导思，启发学生进行数学思考和推理，这是实施有效教学的前提。

例如，教师在教学“分数的初步认识”复习课时，出示三个问题：（1）你能画图表示吗？（2）你能画图表示米吗？（3）关于你还能想到什么？三个问题层层递进，激活学生的已有知识和经验，学生在思考、操作、交流、展示、辨析中加深了对单位“1”的理解。

小学数学课堂教学中，教师要基于学生的学习情况，从学生已有的知识和经验出发，找到学生数学学习的“生长点”，唤起学生的经验，把新知内化后纳入已有的知识结构，将新知识和旧知识联系起来，开启数学思维的大门。

2.顺势而为，疑点激思

学生上课时听明白了，但在做作业或考试时怎么就不会做题了呢？课堂上，教师讲得多，学生被动接受知识，没有思考、提问的时间，就没能真正理解知识，没有形成举一反三的能力。

例如，在学习“平移与旋转”时，学生说推窗、电梯、升旗等现象都是平移运动。旋转门、车轮、螺旋桨的运动都是旋转运动。当一位学生说出摩天轮做旋转运动时，有学生提出了不同看法：“摩天轮是做平移运动。”

教师顺势而为，鼓励学生大胆质疑，让学生积极思考。学生有足够的时间和空间想、做、说、悟，最终明白了：摩天轮在旋转，上面的座舱在平移。整个教学过程中，学生独立思考，小组合作交流，教师因势利导，采取“教什么而不告诉什么”方式，激发学生的求知欲。教基于不教，变被动为主动，培育学生敢于质疑、善于观察、主动思考、敏于求证的良好学习品质。

3.拾级而上，节点展思

数学学习中，学生知识与能力的生成与生长，取决于学生的认知建构状态，学生只有经历知识的建构过程，并将自己的认知与理解展现出来，这样的数学学习才是真实而有效的学习。

数学教学中，教师可将学习活动中的关键环节和核心内容有序地展示出来，充分调动学生的思维，使学生将学习活动不断地内化和概括，并将这些能力迁移到其他学习活动中。在不同的学习活动的关键节点处，教师应鼓励学生将自己的所思所想表达出来，便于教师及时了解学生的学习情况，能看到学生的“学”，看到学生的“会”，看到学生的“想”。

思考能力是学生数学学习的基本能力。只有了解学生真实的思维水平，才能拾级而上引导学生深入地思考。在教学的关键节点处，教师要想方设法展现学生的思考过程，帮助学生提升思维的深刻性，发展学生的数学核心素养。

三、丰富表达能力，充盈素养血脉

数学语言的表达是指在具体的情境中，能借助自己掌握的知识、经验、技能和思想方法，将所思所想用数学语言表达出来。表达是思维的反映，也是促进交流和沟通的重要工具。因此，在课堂教学中，教师应为学生创造表达的机会，培养学生的表达能力。

1.敢于表达，言之有物

在教学中，教师要营造一种能激发学生表达的氛围，让学生想说、敢说，即便学生说得不规范或不正确，也没关系。这样才能让学生在表达中深入思考，进而促进学生语言表达能力和思维的提升。

如何才能让学生有话可说？小学数学教材内容的呈现方式大致有图类、文字类、图文混合类三种。图类：只有图，要把图看明白后，把情境大意讲出来。文字类：只有文字，包括汉字、数字和各种符号，要说出“多”“少”“比”“倍”“除”“除以”“增加了”“增加到”等关键词，要边说边厘清题目中的数量关系。图文混合类：要说全信息，说清图和文、表和文之间的关系。不论是哪种类型，学生都要读懂内容，厘清数量关系，体验获取知识方式的多样性；要读透知识，找到数学与生活的联系。

数学表达的方式有多种，如语言表达、文字表达、图像表达、算式表达、操作表达等。教师要鼓励学生结合实际情况，采用合理的表达方式，立足数学的视角理解知识，做到言之有物，将内在的思维活动与外部的数学表达结合起来，使认知更加明确、思维更加完善。

2.善于表达，言之有理

表达是思维的反映，说理是思维的延伸。学生讲的不但自己懂，还得别人能听懂，既要讲明白思考的物，更要讲明白思考的理，才是善于表达。为此，教师要给学生思考和表达的机会，做一个“讲理”的教师，让学生不仅知道“是什么”，也要知道“为什么”。

例如，在教学“判断一个三位数abc是否是3的倍数”时，教师给学生留下充足的时间探究。大多数学生这样判断：看a+b+c的和是不是3的倍数即可。有的用举例说明的方式判断。也有学生这样做：abc=100a+10b+c，100÷3=33……1，表示每1个百除以3的余数是1，abc中a表示a个百，那么a个百除以3的余数是a个一，即余a；由于10÷3=3……1，即每1个十除以3的余数是1，abc的b表示b个十，因此b个十除以3的余数是b个一，即余b；abc中的c表示c个一。因此，a+b+c理解为百位、十位、个位上的数除以3后的余数之和。经过这样探索和交流，学生能够明白“判断一个数是否是3的倍数要看这个数各位数字之和能否被3整除”的道理。

学生从举例说明、迁移类推到符号表征，连通了知识点之间的联系，多角度建构说理的路径，有条理、有逻辑地把推理过程表达出来，沟通了表达和学习之间的联系。这样，学生的思维就从浅层次走向深入，从言之有物到言之有理，实现了理性能力的增长，极大地提升了学生的语言表达能力。

3.乐于表达，言之有悟

数学中会有一些“规定”，教师对此常常照本宣科，无理可讲。难道课本中的这些“规定”就不用讲？实际上，“规定”的背后有其自身的合理性，也有一定的规律，应该让学生领悟。

例如，在教学“两位数乘两位数笔算乘法（不进位）”时，对于列竖式计算14×12，学生大致有以下三种算法：

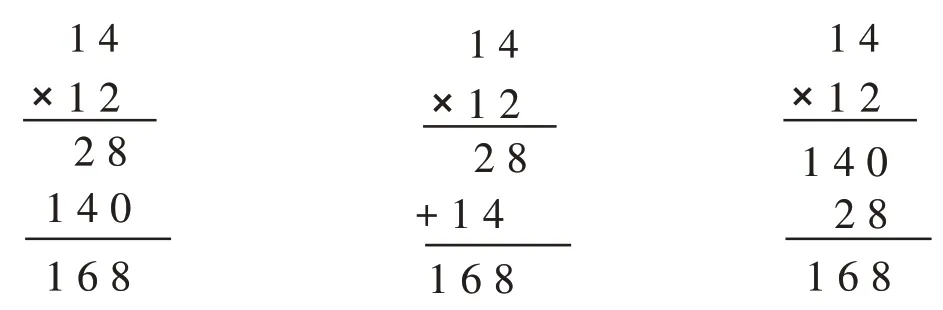
学生说：“第一个竖式中，个位0不写，这是书上规定的。第二个竖式中，‘+’不应该写，也是书上规定的。第三个竖式是错的，不应该先算10×14，应该先算2×14，也是书上规定的。”

教师问：“谁知道为什么要这样规定？结合竖式、图示或学具说一说。”

学生说：“第一个竖式，140中的0在个位上，0可以省略不写，但140中的4表示4个十，因此这个‘4’要和十位对齐，140中的1表示1个百，这个‘1’要和百位对齐。第二个竖式，不写‘+’比较简洁。第三个竖式，应该从个位算起，从十位算起容易出错。”

学生在操作、探索、合作交流中探索算理、归纳算法，经历了困惑、思考、理解的过程，探寻到了知识的本质，理解了“规定”的意义。

在教学本节课之前，教师就这部分内容将人教版、北师大版、苏教版和香港地区的教材做了对比。各版本的教材对笔算乘法中“个位上的0”的写法要求有相同和不同之处。人教版和苏教版教材用虚线框出“个位上的0”，但在表示算式的意义时强调了“个位上的0不写”。苏教版教材还写了省略“0”的简写竖式。北师大版教材写出了“个位上的0”，并结合图形揭示算理，还写出了省略“0”的简写竖式，并用文字和颜色强调了10乘14的积。香港地区教材既没有用虚线框强调“0”，也没有省略“0”的简写竖式。通过对比可以看出，“个位上的0”写与不写，都是人为规定，省略“0”就是竖式的简写形式。其实不省略“0”更符合学生的认知规律，对于初学者来说，笔算乘法竖式时，可以把“0”写出来。

阅读能力是学生的数学学习之根，学生应厚植阅读能力，把粗浅的认识深刻化，把零散的信息系统化，准确揭示事物的本质和规律，夯实自身的数学素养。思考能力是学生的数学学习之本，是数学教育的基本目标。教师应引导学生理性思考，完成个性化的数学学习，为学生搭建数学素养框架。表达能力是学生的数学学习的工具。教师应引导学生将思考过程通过数学语言表达出来，充盈学生的数学素养。