三角形稳定性的数学本质与教法探索
江苏如皋市李渔小学(226500) 任曦
如何理解三角形具有稳定性这一性质?通过查阅词典,笔者发现三角形稳定性中的“稳定”即“不易发生形变”的意思,与“松动”“易变形”的意思相对。
一、“三角形稳定性”的本质
1979年,美国两位学者发表了题为《图形的稳定性》的数学论文,对具有稳定性的几何图形做了系统的梳理和详细介绍:
由一个顶点O引出两条边后能得到一个几何角,如果边可以随意旋转,那么角O的大小、形状就会随之变化,这时图形不具备稳定性。但如果在这两条边上各找一个点,通过一条线段将这两个点(端点)的距离固定(如图1),也就是将PQ的长度固定,那么角O的开口大小就被两个端点的距离“固定”了。此时,几何图形OPQ就是一个三角形,角O的稳定性自然转移为三角形的稳定性。
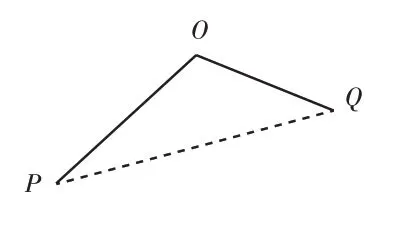
图1
如图2,在任意△ABC中,只要保持三边长度不变,那么任意一条边的长度都可视为连接对应角的两条边的端点的距离,那么三角形三个端点间的距离就不变。于是三角形就不会发生形变,所以三角形具有稳定性。
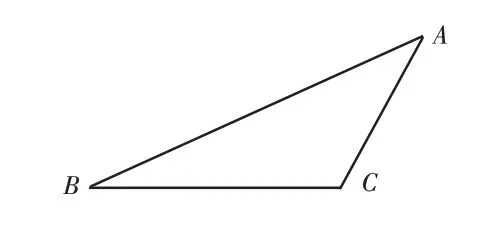
图2
还有一篇关于平面图形稳定性的论文,进一步从几何公式的角度阐释了如何判断图形的稳定性:由拉曼图组成的几何图形才具有稳定性。拉曼图的定义为“在平面内具有稳定性的图形,其边和顶点的数量必须满足这样的数量关系,若顶点数为n,那么边数必为2n-3;若n≥3,那么任意两边的‘断点’必须连接起来”。照此定义,任意一个几何多边形,只要充分连线,都可以转化为拉曼图。
通过计算可知,三角形的顶点数和边数符合拉曼图的定义,三角形是最简单的拉曼图。四边形要获得几何稳定性,根据拉曼图原理,其必须建立4×2-3=5(条)线段。除了四边形所需的4条线段,为了连接不相邻的顶点,还要连接对角线,这样就将四边形分割成两个三角形。同理,五边形、六边形也是一样的操作方式。(如图3)

图3
从理论根源上找到三角形具有稳定性的奥秘,才是对三角形稳定性的最深刻认识。
二、与相关知识的联系
“三角形的稳定性”在人教版教材中被编排在第八册第三章第二课时,是学生学完三角形所有概念后的学习内容。在这之前,学生已经对基本的几何图形及其运动形式有所了解,在第七册中又学习了四边形的易变性,为后续学习三角形的稳定性积累了经验。
但人教版教材在编排“梯形”的内容时,用梯子等稳固的物品引入梯形的概念就不妥当,容易传递梯形具有稳定性的错误信号,误导学生。“三角形的稳定性”是一个重要的性质,它是学生将来在中学学习全等三角形的判断的理论基础。虽然全等三角形的知识在小学不作学习要求,但是小学数学教师要具有前瞻性,合理地进行知识的渗透。
据史料记载,人类历史上首次提出并证明全等三角形的人是古希腊人泰勒斯。他是第一个应用了全等三角形判定定理的人。三百年后,欧几里得对全等概念做了系统阐述,其中有一条被称为万能判定定理的法则——彼此重合的物体是全等的。他还给出了全等三角形的三种判定方法:“角边角”“边边边”“角角边”。其中,“边边边”的判定方法与三角形的稳定性不谋而合,即如果三角形三边长度固定,那么三角形的形状也唯一确定。三角形稳定性的用途十分广泛,涉及地理、建筑、外交、军事、政治等领域。例如,要想形成稳定的外交关系,就要努力建立“三足鼎立,互为犄角”的外交关系。反之,要破坏稳定,则要破坏这种三角结构。
到了初中,学生的理论水平大幅提高,学生就会思考:为什么所有的几何图形中只有三角形存在全等的概念,而其他图形则没有这个提法?从而发现,因为三角形具有稳定性,而三角形稳定性的来源恰好可以作为全等的判定依据。所谓全等,实际上就是对三角形形状、大小的唯一性做出确认,在这个三角形的形体唯一性被确认后,按照这种“尺码”打造的任何三角形都是这个三角形的复制品,它们统统全等。也就是说,任意一个三角形的形态都是独一无二的,凡是相同者必然有符合促成其稳定性的全部特征。
三、教学设计思路
三角形的稳定性是三角形的本质属性,是客观存在的几何特征。教学目标可以确立为“探究三角形三边长度对三角形形状结构稳定性的影响”。要顺利完成教学目标,不妨让学生经历观察、猜想、验证、应用等数学过程,逐渐体会三角形的稳定性。
【第一环节】理解稳定性的概念
人教版教材对稳定性没有出具合理的权威解释,且编排的“梯形”内容还从稳固的实物中提炼出不稳定的梯形,这容易对学生造成负迁移。因此,在课堂引入阶段提出要求:请你解释什么是几何意义上的“稳定”,试着举出几个例子。目的是让学生领悟这里的“稳定”是指图形的形状、大小不变,为之后的研究扎根。
这一环节中,学生需要结合自身经验,先回顾什么是物体的稳定,再通过操作研究出三角形一边长短可以决定其对角的开口大小,探明三角形三边长短决定三角形的形状、大小,从而提出猜想。教师紧接着从角引入稳定性,提出类似“用两根长度固定的木棒做试验,想一想,如何添加学具才能制作一个大小不变的角?”的问题,启发学生想到用第三根木棒来固定,构成三角形。
【第二环节】学生观察和操作
通过“如果第三根木棒的长度有变化,角和组成的图形会发生什么变化?四人一组,交流和归纳自己的发现”这样的任务,让学生体会三角形三边长短决定了其形状大小,并联系前面提到的稳定概念,提出三角形具有稳定性的猜想。此外,可以让学生完成“用木棒拼摆各种不同的多边形,看看是否可以随意变形”“要使其具有稳定性,可以如何操作”等任务,让学生体验到三角形才是最稳定的基本几何图形。
学生观察图形的变化情况,发现三角形边、角、形三者之间的制约关系,发表观点并讨论。
【第三环节】验证猜想,得出结论
经过上一环节,学生已经明确三角形的形状由三边长短决定,本环节就只待证明。考虑到三角形的稳定性与全等三角形的关系,这一环节中教师应鼓励学生寻找更多成就了三角形的稳定性的因素。
【第四环节】三角形稳定性的应用
由于学生个体间存在差异,应用环节应分层设计任务,兼顾全体学生。针对后进生,设计诸如“寻找具有三角形稳定结构的物品”的活动;针对中等生,则设计诸如“设计具有三角形稳定性的物品并说明设计思路”的活动;针对优等生,则可将三角形的稳定性从几何领域引申到外交策略,实现学科融合。
例如,美国和朝鲜关系紧张,中国如何在保证自身安全的情况下,妥善处理与美国和朝鲜的关系?教师让学生分小组查阅资料,利用三角形的稳定性,想一想作为一名外交官,应如何处理与美国和朝鲜之间的外交关系。
三角形之所以具有稳定性是因为三边、三角相互制约,形成三足鼎立、互为犄角的局面,三边三角互相牵制。也就是说,三角形的角、边形成了“一荣俱荣,一损俱损”的联盟关系。以此类推,生活中凡是具有三方势力相互制约的情形,都可以形成稳定结构,比如三角关系、三脚架、三国外交等,这些都是对三角形稳定性的升华和拓展。
作业的层次可由学生自主选择,也可由教师根据课堂情况灵活处理,比如给出两个任务,由学生任选其一。因为学生的任务不相同,最好能留到课后完成,然后课上汇报交流。
在教学“三角形的稳定性”时,所有的数学活动既要符合学生的心理特征,又要契合数学本质规律,让学生的观察、操作等系列数学活动都能直击数学知识本质,从而深刻揭示三角形具有稳定性。
本节课的教学能让学生拥有更自由的探究空间。学完后,学生在知识方面有了很大的收获,包括三角形稳定性之外的全等,及决定三角形稳定性的因素等。在个人能力方面,既有独立思考,又有合作探究,在交流分享中学生的协作意识和交流意识得到提升。
值得强调的是,教学有法但无定法,教师需要根据实际情况,灵活选择适合自己和学生的教学方法。

