频域临界面法求解多轴损伤的研究

高峰，阳光武，肖守讷，肖绯雄

(西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

0 引言

在轨道交通领域，车辆在运行时，会受到各种由于轨道不平顺而产生的随机载荷谱的影响。随着我国铁路大提速，轨道车辆的运行环境越来越恶劣，轮轨之间的振动变得更加强烈，结构件受到的多轴随机振动载荷急剧增加，因此在随机激励下产生的多轴疲劳问题就越来越受到重视。

针对多轴问题，目前都是将多轴等效成单轴，再通过单轴的方法予以解决。等效过程分为两种，一种是在时域内进行等效，另一种则是在频域内等效。时域具有表达周期性载荷方便的特点，但其若想完整地表达加载历程，必须要有完整的信号数据。若设备复杂且运行时间长，数据处理就会耗时又繁琐。而频域的理论就很好地避免了这个问题。在频域内应用多轴疲劳准则将多轴应力功率谱或应变功率谱等效为单轴应力或应变功率谱，再通过单轴疲劳理论里疲劳公式中的统计参数从而得到结构件的疲劳寿命。该方法计算量小，耗时短，在工程应用中更具有适用性。

目前针对频域疲劳主要有3种分析方法，分别是应力不变量法、能量法和临界平面法[1-4]。应力不变量法中最准确的就是CRISTOFORI等提出的PbP(projection by projection)法[5]，虽然该方法全面地考虑各个应力分量对疲劳寿命的影响，但由于该方法参数过多且难于获得，并不太适用于实际工程问题。能量法认为塑性功的累积最终导致了结构的破坏，而临界平面法确定了临界损伤平面的位置且疲劳破坏面的物理意义明确，因此被广泛认为是解决多轴疲劳问题的有效方法。临界平面法最重要的就是确定临界平面，本文通过编写损伤累积法确定临界平面位置的相关程序，再通过等效的应力功率谱结合Miner线性损伤累积理论和Dirlik经验公式求得结构的预期寿命[6]，并通过时域瞬态分析和对比数据，验证该方法的准确性。

1 理论分析

1.1 基于临界平面的应力准则

20世纪80年代末，MACHA E[7]首先在频域内提出了基于临界平面法的多轴疲劳失效准则。这些准则在多轴随机载荷下的一般形式可由式(1)表示。

σeq(t)={σij(t),P,C}

(1)

式中：σij(t)为应力或应变分量；P为定义临界平面所需的参数；C为材料参数。

基于临界平面上的应力准则分为以下3种，分别是基于临界平面上的最大正应力准则、基于临界平面上的最大剪应力准则、基于临界平面上的最大正应力和剪应力准则[8]。

本文采用基于临界平面上的最大正应力和剪应力准则，即临界平面由最大剪应力作用的两个平面中一个的平均位置决定(B=1,K≠0)。则等效应力计算公式如式(2)所示。

(2)

式中：σij(t)，(i,j=x,y,z)为应力分量；ln、mn、nn(n=1,2,3)为应力主轴的方向余弦；K为材料参数。

9个主应力轴的方向余弦ln、mn、nn可由3个欧拉角来表示。欧拉角是用来确定刚体定点转动后刚体位置的3个角参量，由自转角φ、章动角θ、进动角ψ表示。欧拉角的定义如图1所示。图中Oxyz为固定的直角坐标系，O为原点，Ox′y′z′为固连刚体的直角坐标系。刚体先绕固定坐标系中的z′轴逆时针转动φ，再绕固连的x′轴即图中的N轴逆时针转动θ，最后绕z′轴逆时针转动ψ。

图1 欧拉角的定义

经过变换，ln、mn、nn与欧拉角(θ、ψ、φ)可由式(3)表示[9]。

(3)

1.2 基于损伤累积法确定临界平面寿命

在确定载荷的情况下，损伤累积法是通过概率密度函数计算空间中各个平面的累积损伤，累积损伤最大的平面即寿命最小的平面为临界平面[10]。

基于临界平面上的最大正应力和剪应力准则，可设a1,a2,a3,a4,a5,a6，其形式如式(4)所示。

(4)

结合式(4)可将式(2)改写成式(5)：

(5)

应力功率谱矩阵如式(6)所示。

(6)

等效的应力功率谱密度可由式(7)表示。

(7)

式中：Gkk(f)为应力分量σ(t)的自功率谱密度函数；Gkl(f)为应力分量σ(t)的互功率谱密度函数。

将得到的等效应力功率谱通过式(8)求各阶谱矩：

(8)

再通过Dirlik给出的Dirlik经验公式得到式(9)应力幅值概率密度函数p(S)：

(9)

应力幅值S在区间(S-dSi,S+dSi)的概率P(Si)为

P(Si)=p(Si)dS

(10)

则时间T内应力幅值落在区间(Si-dS,Si+dS)的次数ni为

ni=VpTp(Si)dS

(11)

进而可得在区间(Si-dS,Si+dS)内结构所受的损伤量为

(12)

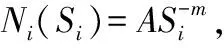
最后根据Miner线性疲劳损伤累积理论，总损伤由式(13)表示。当总损伤为1时结构达到破坏，结构的寿命T可由式(14)表示。

(13)

(14)

1.3 分析流程

通过有限元软件随机振动分析可得危险点各应力分量的功率谱，将之代入上述方法的程序中，最终求得结构寿命。具体流程如图2所示。

图2 基于损伤累积法确定临界平面流程图

2 有限元仿真分析

2.1 有限元模型概述

模型由1个3 mm厚的6061-T4板和2个50×20×10 mm的Q235配重块组成。其具体尺寸如图3-图4所示。板材弹性模量E=69 000 MPa，泊松比μ=0.33，密度ρ=2 750 kg/m3。配重块弹性模量E=210 000 MPa，泊松比μ=0.3，密度ρ=7 800 kg/m3。S-N曲线根据EN1999-1-3中铝合金母材71-7，其材料参数k=7,C=1.8×1019。

图3 试件俯视图

图4 试件有限元模型

将板材方形部分进行固支约束，通过模态分析得到试件的1阶垂弯频率为29.32 Hz，1阶侧弯为98.46 Hz，1阶扭转为126.9 Hz。

2.2 频域随机振动分析

在板材方型部分通过rigid单元连接大质量点，对其在x、y、z3个方向上施加相同固定幅值的限带白噪声激励。为验证功率谱幅值以及远离共振频率的频率区间是否对结构损伤产生影响，设置以下3个工况。其中工况1的截断频率为10～150 Hz，幅值为0.010g2Hz；工况2的截断频率为10～150 Hz，幅值为0.008g2Hz；工况3的截断频率为10～200 Hz，幅值为0.008g2Hz。频域内的激励信号如图5-图7所示。

图5 工况1加速度功率谱密度曲线

图6 工况2加速度功率谱密度曲线

图7 工况3加速度功率谱密度曲线

单轴累加需要分别计算结构在各方向上受到激励时的功率谱密度。各工况各轴向激励下的应力功率谱如图8-图10所示。

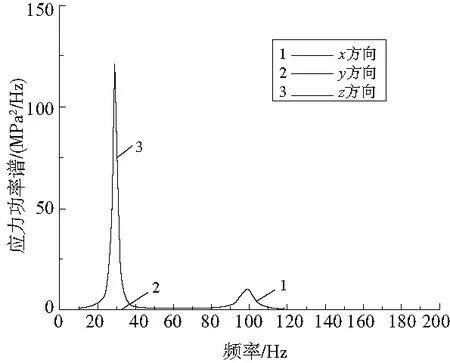
图8 工况1各单轴激励下应力功率谱密度曲线

图9 工况2各单轴激励下应力功率谱密度曲线

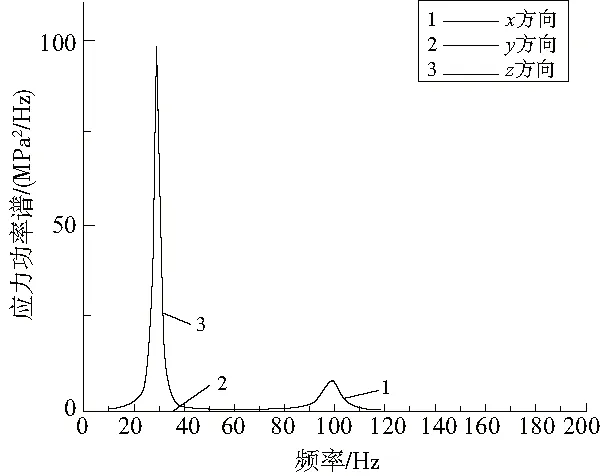
图10 工况3各单轴激励下应力功率谱密度曲线

多轴同步通过临界平面应力准则将危险点各应力分量的功率谱转换成等效应力功率谱。同时得到了临界平面3个欧拉旋转角(θ，ψ，φ)，分别为4.59°、48.13°及120.33°。表1为3种工况下等效应力功率谱的各阶谱矩，图11-图13为3种工况下的等效应力功率谱。

表1 3种工况下各阶谱矩

图11 工况1等效应力功率谱密度曲线

图12 工况2等效应力功率谱密度曲线

图13 工况3 等效应力功率谱密度曲线

2.3 分析结果对比

时域激励是将白噪声激励通过逆傅里叶变换得到，因白噪声频谱对应无限多种随机时间序列样本，故选取多次时间序列由瞬态分析法求平均值。表2对比了单轴线性累加法、临界平面法和时域法得到的3种工况下模型的疲劳寿命结果。图14给出了3种工况下模型在3种计算方法下的疲劳寿命结果对比。

表2 3种工况下模型3种方法计算的疲劳寿命结果

图14 3种工况下模型3种方法计算的疲劳寿命结果对比

由结果对比可知，在3种工况下，时域的损伤最大，其次是临界平面法，而单轴累积法计算的损伤比前两种方法小很多。且幅值的变化会对结果产生很大的影响，远离共振频率的频率区间依旧会对结构产生一定的损伤。在工程中，一般通过时域分析得到的寿命较为准确。故将时域分析得到的寿命作为标准，可知临界平面法与时域分析得到的寿命误差在8%以内，比单轴累积法计算的误差小得多。分析临界平面法的误差有以下两点：

1)本文程序基于复化梯形公式求解的数值积分，可能存在一定的误差；

2)本文编写程序中旋转欧拉角的角度步长根据文献[11]选取的0.01 rad，其精度会对结果产生一定影响。这个旋转的角度越小精度越高，但随着步长缩小10倍，计算时间会增加103倍。

3 结语

轨道车辆及其设备运行时间长，受载情况复杂，通过时域瞬态分析预测寿命并不太适用。目前，对于工程上的多轴问题，大都采用提高输入激励谱，分别计算三轴向损伤再线性累加，但该方法并不能反映各轴向间激励的影响。针对上述问题，本文提出通过采用损伤累积法求临界平面的频域法，给出了实现该方法的具体流程，并与时域分析得到的寿命进行对比，误差远小于单轴累加法。该方法易于编程，明确了损伤平面的位置，给轨道车辆及其零部件寿命预测提供了参考。