新型摇摆隔震装置振动台试验研究

黄浩鸣,陈征林,魏陆顺

(佛山科学技术学院 交通与土木建筑学院,广东 佛山 528000)

0 引 言

隔震结构体系是在建筑中设计柔性隔震层，地震产生的能量在向上部结构传递的过程中被隔震层吸收，从而降低上部结构地震作用[1]。从1963年开始，部分学者发现摇摆中的细长结构稳定性更好，更不容易发生倾覆，提出了考虑摇摆倾覆效应的结构模型，对比传统结构最大变形有着明显的减少[2]。2005年T.Shimada[3]设计了一种用于核电站的三维隔震系统，由空气弹簧和液压抗摇摆装置组成的，并进行了振动台试验研究。2017年徐力[4]基于结构摇摆设计思路，将RC框架中普通框架柱上下端约束变成铰接，形成摇摆柱，将黏滞阻尼器植入结构,利用其耗能来减小变形，研究该结构的抗震性能。2020年夏修身[5]等对一简支梁缩尺模型进行振动台试验，研究模型桥墩动力特性及摇摆反应，结果表明结构具有良好的抗震及自复位性能。郭展[6-7]等提出了设置高阻尼橡胶垫块和线性弹簧的两种基底摇摆隔震桥墩模型，通过振动台试验和数值模拟，对两种摇摆隔震桥墩的地震响应规律和抗震性能进行了对比研究，试验得出了该新型桥墩能够显著降低墩顶水平加速度和墩底应力值，但同时会增大墩顶水平位移的结论。任逸飞[8]等根据隔震层橡胶支座的竖向变形计算结果，将高层隔震结构的摇摆状态分成未提离、提离、摇摆和倾覆状态，提出了基于简化刚体模型的提离摇摆状态分类方法。总体上，有关摇摆隔震技术和装置的研究处于起步阶段，其装置构造设计有着很大的发展空间，以及其力学性能在学术界仍没有统一的分析模型，需要广泛深入的研究，并且目前摇摆隔震技术仍未应用于塔型结构。为此，针对塔型结构在地震作用下产生的变形问题，提出一种新型的摇摆隔震装置，运用摇摆隔震悬臂梁分析模型，通过振动台试验分析，探究装有该装置的塔形结构对比传统结构的隔震效果。

1 摇摆隔震模型

摇摆隔震悬臂梁模型如图1所示。

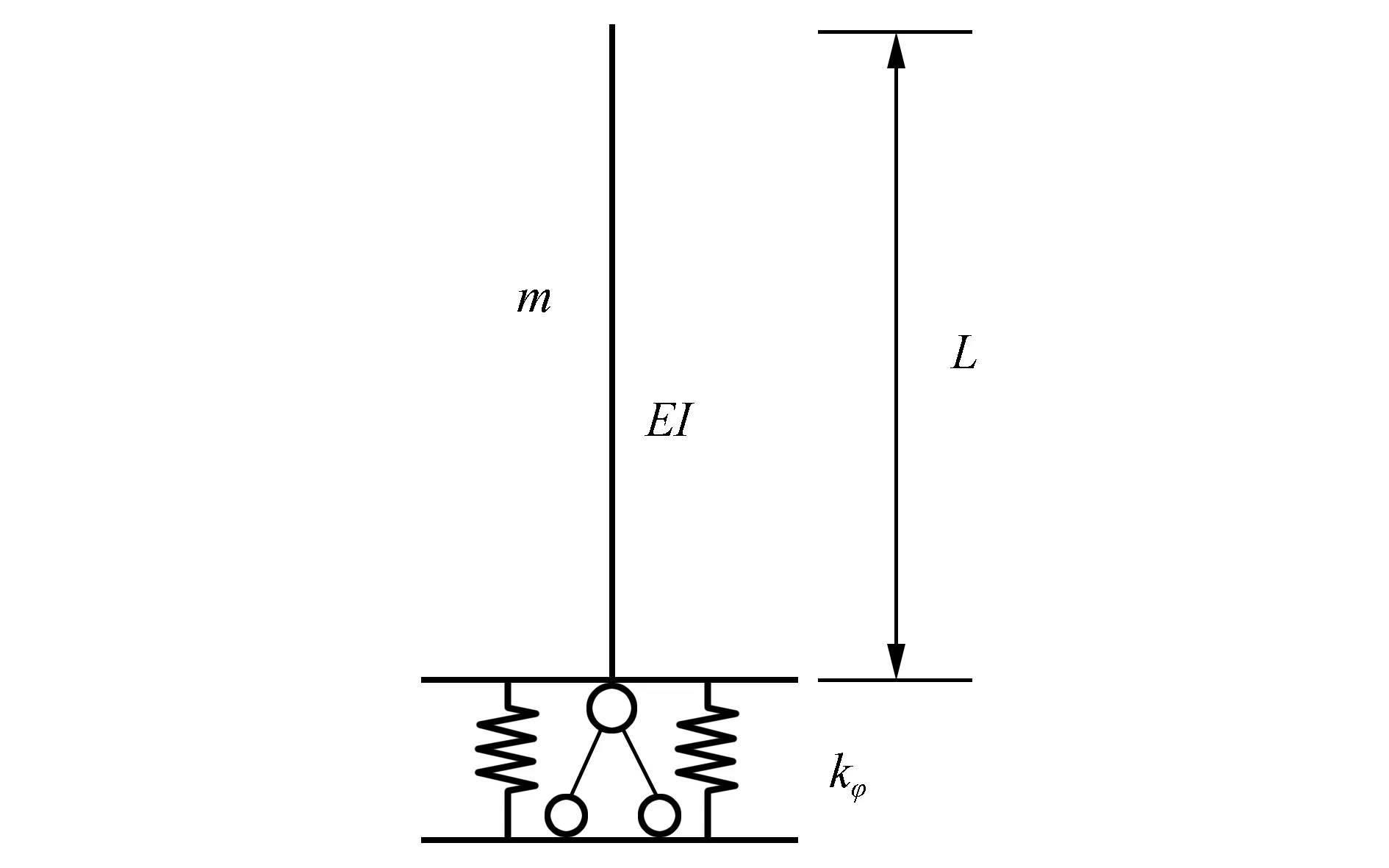
图1 摇摆隔震悬臂梁模型Fig.1 Model of a rocking vibration isolation cantilever beam

根据伯努利-欧拉梁理论，摇摆隔震结构振动方程为：

(1)

采用分离变量法，设定解为：

v(x,t)=Φ(x)Y(t)

(2)

通解为：

(3)

摇摆隔震结构边界条件为：

在x=0处：

Φ(x)=0，kφθL=M=EIΦ″(0)

(4)

在x=l处：

M=EIΦ″(1)=0，v=EIΦ″(1)=0

(5)

将边界条件代入方程，摇摆隔震频率方程：

(6)

式中：kφ为隔震层抗摇摆刚度；θ为结构偏转角度；L为上部结构长度。

进而求解得结构的自振频率ω和振型Φ(x)。则结构的任意一点位移为：

(7)

在此基础上，本文设计了一种新型摇摆隔震系统，强震作用下当结构上部地震弯矩超过球铰提供的抗倾覆力矩，结构利用提离摇摆实现隔震。

2 振动台试验概况

隔震装置由上下连接钢板和4个钢弹簧、万向球铰构成，球铰通过螺栓与上板和底板相连，连接板尺寸为500 mm×500 mm厚度均为10 mm，内布置弹簧均采用线径8 mm的高强弹簧，其高度为90 mm，内径为55 mm，外径为65 mm，单个弹簧抗压刚度为53.7 N/mm，弹簧安装于距装置中心175 mm处，隔震装置构造见2图，图3为隔震装置实物图。

图2 新型摇摆隔震装置构造图Fig.2 The sketch picture of new type of rocking isolation device

本试验结构原型为高12 m、重2.7 t的高耸塔型电力设施。考虑到振动台实际最大承载能力，上部结构采用缩尺比1∶5的钢结构模型，上部结构模型采用Q235钢空心圆钢管，截面尺寸为50 mm×42 mm×4 mm，高2.52 m，表1为模型结构相似系数表。结构焊接于装置上连接板。当隔震装置发生竖向位移时，万向球铰不发生转动，竖向承载力由弹簧提供。当上部结构发生水平位移时，万向球铰随着上部结构平动而转动，则上连接板运动形式将会由平动转换为上下摇摆动，弹簧为其提供一定的抗摇摆刚度。

图3 新型摇摆隔震装置实物图Fig.3 The physical picture of new type of rocking isolation device

表1 模型结构相似系数表Table 1 Model structure similarity coefficients table

试验中采用压电式三向加速度传感器、拉杆式位移传感器测量模型结构动力响应；采用电阻式应变片测量上部结构底部轴向应变。具体测点布置如图4所示。

试验选用试取2组实际的地震动记录和1组人工波作为振动台输入，分别为El Centro波、Taft波和人工波。试验加速度幅值调幅分别为0.2g、0.4g和0.8g。先在未加装隔震装置的模型结构进行振动台试验，完成所有工况后，再进行加装隔震装置的模型结构。所有工况均为X单向输入。

3 试验结果分析

各加载工况下，传统结构模型和摇摆隔震模型均呈现出往复摇摆运动的特点。

图4 传感器测点布置Fig.4 Layout of sensor measuring points

在传统结构模型试验中，在0.2g试验工况下，结构产生摇摆运动的运动特性，结构摇摆运动不明显。在为0.4g试验工况下，结构发生明显摇摆运动。在0.8g试验工况时，结构摇摆运动十分剧烈。在地震波输入结束后，结构仍然有较大的响应且不容易静止，结构顶部水平方向仍有晃动。

在摇摆隔震模型试验中，在0.2g试验工况下，隔震层发生微弱上下摇摆，上部结构发生明显摇摆运动；当在0.4g试验工况下，隔震层发生轻微上下摇摆，上部结构呈现剧烈摇摆运动；在0.8g试验工况下，隔震层发生明显上下摇摆，上部结构摇摆运动十分剧烈。在地震波输入结束后，结构很快即停止振动。在0.4g和0.8g工况中传统结构在地震波激励结束后仍有小幅振荡，隔震结构则在地震波激励停止约5 s内即可停止振动，隔震装置能很好地抑制结构的自由振动。

图5、图6和图7分别为不同绝对加速度响应幅值下的El Centro、Taft和人工地震波下非隔震结构模型顶部和隔震结构模型顶部加速度响应图。

图5 0.2g工况下结构顶部加速度时程对比Fig.5 Comparison of acceleration at the top of the structure at 0.2g condition

图6 0.4g工况下结构顶部加速度时程对比Fig.6 Comparison of acceleration at the top of the structure at 0.4g condition

图7 0.8g工况下结构顶部加速度时程对比Fig.7 Comparison of acceleration at the top of the structure at 0.8g condition

各工况下结构顶部绝对加速度响应幅值对比及隔震效果见表2。

表2 各工况结构顶部加速度峰值对比Table 2 Comparison of peak acceleration at the top of structure under different working conditions

从图5～图7和表2可看出：

1)传统结构和隔震结构顶部加速度响应在0.2g地震波工况下，El Centro波的结构上部加速度响应最大，人工波次之，Taft波最小。而在0.4g和0.8g地震波工况下，Taft波的结构上部加速度响应最大，El Centro波次之，人工波最小。

2)对于同一地震动的激励下，结构上部的加速度响应均随着地震强度的增加而逐渐增大，隔震装置的隔震率也随着提高。隔震率高达12.3%～33.5%，有显著的隔震效果。

从上述结论可知，隔震装置在0.2g工况下装置未到达理想的预设启动加速度峰值，而在0.4g和0.8g工况下装置发挥出良好的隔震效果。

图8为不同绝对加速度响应幅值下的El Centro、Taft和人工地震波下传统结构模型顶部和隔震结构模型顶部位移响应峰值趋势图。各工况下结构顶部位移响应幅值对比见表3。

图8 顶部位移响应峰值趋势Fig.8 Envelope diagram of peak displacemen response

从图8与表3数据可看出：

1)在台面激励加速度峰值相同的每组地震波工况中，El Centro波作用下结构上部位移响应最大，人工波次之，Taft波最小。与图5～图7反映出的加速度峰值大小规律一致。

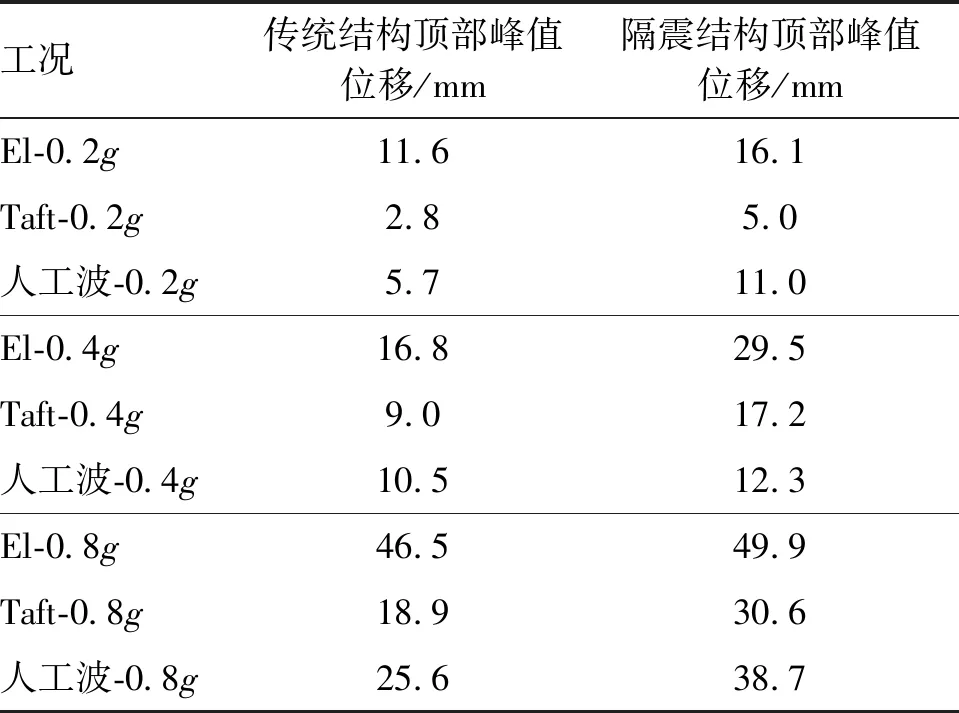
表3 各工况结构顶部位移峰值Table 3 Peak displacement at the top of the structureunder different working conditions

2)各工况下隔震结构顶部位移幅值均大于传统结构顶部位移幅值。隔震装置中装有球铰，因此结构底部相当于铰接，而传统结构底部为固结，两者有实质性区别，所以位移响应差距较大。摇摆隔震装置会使上部结构从水平运动的方式转变为摇摆运动，在明显减少结构顶部加速度的同时，会小幅度增加顶部的位移。

3)隔震结构位移响应幅值随地震波激励加速度峰值的增大约呈线性递增关系。由于本次试验是一次性完成的，摇摆隔震装置中的弹簧在经过0.8g工况的El Centro波和Taft波后，发生了塑性变形，因此从0.2g的人工波开始，隔震结构顶部的位移峰值响应变化较为偏离弹性变化，但从整个试验结果的趋势表明，在隔震装置的作用下，结构基本保持弹性状态。

表4为传统结构和摇摆隔震结构底部应变对比。由表4可看出传统结构和隔震结构底部应变幅值随地震波激励加速度峰值的增大而增大，与图5～图7反映出的隔震结构顶部加速度峰值大小规律一致。在各工况下隔震结构底部应变值均远远小于传统结构底部应变值。对于同一地震动的激励下，随着地震强度的增加，隔震装置的应变衰减效果是增强的，应变衰减率高达67%～85%，其中人工波最大，El Centro波次之，Taft波最小。这是由于隔震装置设置了万向球，从基底由固结转变为铰接，球铰的转动释放了基底弯矩使得结构底部应力值减小，进而结构的应变值也随之减小。

表4 结构底部应变对比Table 4 Comparison of strains at the base of the structure

4 结 论

本文对摇摆隔震结构缩尺模型进行了加装摇摆隔震系统和未加装隔震系统的振动台试验，试验结果表明：

1)设计制作了新型摇摆隔震装置，该装置利用万向球铰实现摇摆，弹簧产生压缩变形实现耗能隔震，通过预压弹簧实现恢复功能，装置构造合理且传力路径清晰。

2)在输入0.2g地震动加速度下，装置效果不明显。当输入地震动加速度越大时，隔震装置隔震效果越明显，表明了摇摆隔震装置的预设启动效果和隔震效果良好。摇摆隔震结构模型加速度响应相对于传统结构有所减小，并且隔震效果随着地震动的输入峰值增大而增加，隔震率高达33.5%。

3)摇摆隔震结构和传统结构顶部水平位移峰值随着地震动加速度峰值增大而增大，但摇摆隔震结构模型位移峰值相对于传统结构有所放大，这种特性是由于隔震装置下的万向球铰造成的，球铰转动使得结构底部相当于铰接，进而是结构上部位移响应增大。摇摆隔震结构底部应变值均远远小于传统结构底部应变值，应变衰减率高达85%。