一种广义Bodner-Partom黏塑性本构模型

王常宇，徐可君，秦海勤，马中原，谢静，谢镇波

海军航空大学 青岛校区，青岛 266041

航空发动机的热端部件受载情况颇为极端和复杂，因此，作为结构完整性研究的基石，描述高温合金材料力学行为的本构关系尤为重要。在复杂载荷下，经典弹塑性理论和蠕变理论[1]由于无法预测后继屈服面、强行区分时间无关的塑性和时间相关的蠕变以及每步计算都须判断屈服面等问题导致误差较大。于是，一些基于细观过程的、唯象的内变量黏塑性统一本构理论逐渐兴起，典型代表如带屈服面的Chaboche模型[2]、Waller模型[3]和无屈服面的Bodner-Partom模型[4]、Miller模型[5]等。其中，被认为是“力学里程碑式”的Bodner-Partom本构理论(B-P模型)直接从位错动力学出发，绕开了传统屈服面概念，认为各种力学行为特性耦合于全形变过程，都由基于微观机理而演化的内部状态变量控制。该模型在表征能力、微观机制支持和数值计算便利性等方面具有相当的优势，故而应用广泛[6-10]。

几十年来，相关学者在B-P理论基础上进行着探索，以追求力学行为的完美表述以及本构方程的简约。Khen和Rubin[11]假设硬化系数是各向同性和各向异性变量的函数，改进的模型更为满足复杂循环加载下的响应特征；周益春和段祝平[12]通过引入损伤变量，修正了Mises准则带来的非弹性体应变率为零的不合理结果；Shi等[8]提出了内变量具有不同硬化趋势的假设，由此发展出的新内变量演化模型可改善对单调拉伸和循环硬化的模拟精度；Sun等[13]将新的损伤演化方程引入B-P模型，新模型的应变率敏感性、损伤演化以及卸载特性表明应变软化等动态行为的建模得到了优化。

尽管B-P模型在模拟材料的率相关非弹性功硬化特性方面精度可观，且能够模拟某些循环蠕变[14-15]，但尚面临一些问题[6,16-19]没有解决：① 在描述循环硬化/软化等特征时滞回曲线存在“过方”(Oversquare)和饱和过快现象；②以Mises流动法则作为基本假定。这可能限制了对材料黏塑性的描绘能力，比如循环应力松弛、平均应变循环蠕变(又称棘轮，Ratcheting)等现象。显然，发展能够解决上述问题、更全面和精确地反映材料的率相关黏塑性行为而又控制数值计算实现难度的黏塑性本构方程，对于高温材料寿命与可靠性分析具有重要的应用意义。

基于以上，本文的工作是：以B-P统一黏塑性本构理论为基本框架，利用率相关的屈服势函数直接由黏塑性应变流动的正交法则导出本构关系；在运动硬化演化方程中引入黏塑性应变率修正项并考虑动态恢复的非线性特征，发展了新的硬化准则，从而构建了一种广义的B-P本构模型。利用镍基粉末高温合金FGH96(航空发动机涡轮盘材料)在使役条件下的试验数据对广义B-P模型的有效性和适用性进行了与原始B-P模型的对比验证。

1 广义B-P统一黏塑性本构理论

(1)

弹性部分服从广义Hooke定律：

(2)

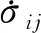
1.1 流动法则和运动方程

一般情况下，表达方向性硬化效应的黏塑性形式流动法则为

(3)

式中：λijkl为表达方向性硬化的四阶张量乘子；Skl为应力偏量。

B-P模型以Mises材料为基本假定，此时式(3)简化为Prandtl-Reuss流动理论的各向同性形式[21]：

(4)

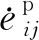
将式(4)两端二次自点积，得

(5)

(6)

(7)

Bodner、Partom等根据位错动力学理论给出控制塑性应变的运动方程：

(8)

式中：D0为极限剪切应变率；n为材料应变率敏感性常数，与载荷历史无关；Z为载荷历史相关的内部状态变量，体现材料抵抗塑性流动的硬化状态。

联立式(6)～式(8)，可得

(9)

(10)

(11)

(12)

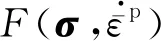
(13)

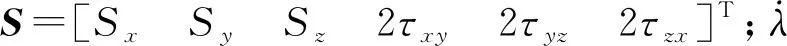
(14)

(15)

将式(11)代入式(15)，得

(16)

于是，有

(17)

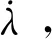
下面可推广至包含内变量Zi的一般情况。若定义屈服势函数Φ为

(18)

则由正交法则：

(19)

(20)

流动法则即得到确定。

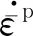
1.2 内变量演化方程

B-P模型的内变量Z由各向同性分量ZI与运动硬化分量ZD组成：

Z=ZI+ZD

(21)

式中：

ZD(t)=βij(t)uij(t)

(22)

标量ZD是硬化张量βij对表示应力方向的基张量uij的变换结果，所以材料运动硬化的演化特性由βij表达。将演化方程由(原B-P模型)：

(23)

改写成：

(24)

上述修正的原因和意义在于：

1) 统一黏塑性本构理论一般认为率相关的力学行为由某一个主导的应变率因子表达即可，其他因子影响可忽略，B-P模型的演化方程即是基于硬化速率方向与塑性变形速率相同的假设[21]。而在微观尺度上，障碍物处位错的热激活主导着塑性动力学。由于动态恢复现象，应变硬化在很大程度上取决于进程的温度和应变速率。当演化方程由多项组成时，内部变量不完全依赖于演化方向[22]，因此拓展不同的硬化/恢复演变方向有利于揭示屈服和饱和应力附近的重要行为，Kocks和Mecking[23-24]的研究也佐证了这一点。

2) 研究[25-26]发现材料在塑性变形过程中，屈服面会改变形状(沿局部法向)。B-P理论是“无屈服面”的，或从另一个角度可以说它的屈服面是由变量控制而动态变化的。对于原始B-P模型，演化方程的硬化方向即σ方向、恢复方向即β方向。这意味着后继屈服面在应力空间的相似放缩和平移是被考虑的而翘曲(带角度)是被忽略的，这是Mises屈服准则带来的限制。同时，非弹性应变随循环而不断累积的行为没有被考虑，这是现有模型不能很好地描述棘轮现象[27-29]的原因之一。另外，在演化方程中引入塑性变形历史作为尺度利于描述包辛格效应。

比例加载与非比例加载下，各向同性硬化分量的演化方程分别为

(25)

(26)

(27)

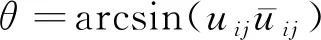
2 计算方法

广义B-P模型包含18个材料参数：E,D0,Z0,Z1,Z2,Z3,Z4,m1,m2,n,A1,A2,r1,r2,r3,r4,r5,f1，非比例加载时还包括Y1。

一般可取A=A1=A2；r1=r2；Z0=Z2，应变速率小于10 s-1。这些参数可以通过材料的单轴拉伸试验、控制应变的对称循环试验、蠕变试验和控制应变的非对称循环试验，结合一定的优化算法(如Levenberg-Marquadt方法)得到。

统一黏塑性本构方程大多以率形式给出，通常采用径向回归法[9,30-31]以恰当的积分运算将率形式转化为增量形式。计算的核心问题是由微过程的增量应变分别求出弹性和非弹性的增量应变dεe和dεin，进而求出增量应力dσ。在下列推导中，如无特殊说明，所有的量均指t+dt时刻。

将式(2)隐式积分并写成偏张量形式：

(28)

(29)

在径向回归过程中有：

(30)

上标tr表示试探值。将式(29)积分后代入式(28)，可得

(31)

两边二次自点积，得

(32)

(33)

对于本文模型，由式(2)、式(19)、式 (20)，有增量方程如下：

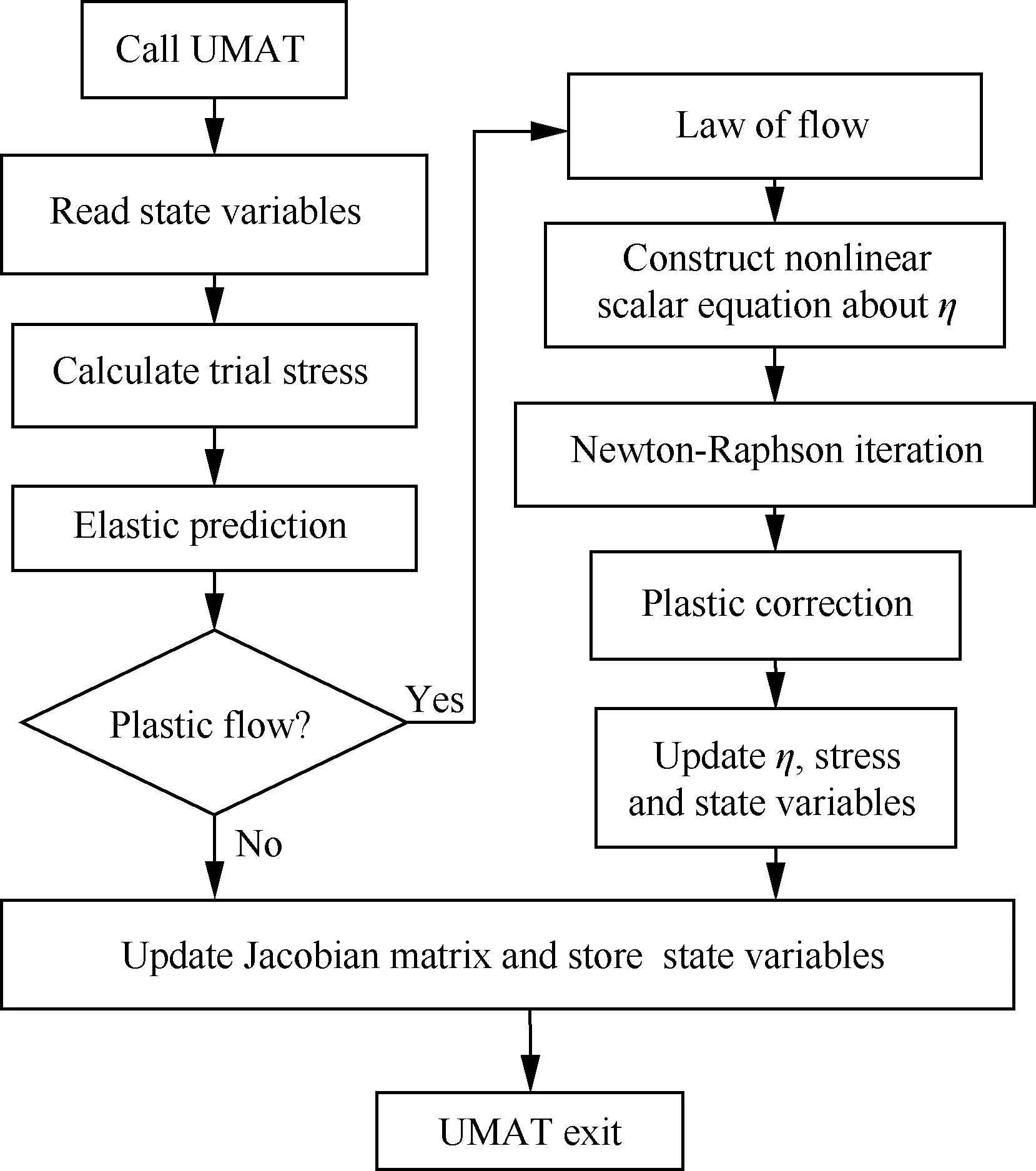
图1 UMAT流程图

(34)

(35)

dσ=M:(dε-dεp)

(36)

由内外状态量σ、Z解得dt的增量应变dε后，通过式(36)解出dλ、dεp和dσ。内变量增量由演化方程给出。

3 数值分析与试验验证

表1 FGH96合金主要组分

图2 拉伸、疲劳及疲劳-蠕变试件

见图3，当变形进入塑性应变率主导阶段时，应变率效应逐渐显著，此时B-P模型响应较为滞后，出现偏离。相较之下，新模型由于对材料的硬化演化趋势的包容度更高，所以曲线后半段的模拟精度更高。图4中的对比显示了新的内变量演化方程在循环累积下的松弛能力，即表达平均应力循环松弛的能力。图5和图6表明模型显著改善了对应力应变滞回曲线的模拟效果，因为“过方”和饱和过快现象消失了。对FGH96合金非弹性变形特征的建模验证了本文模型的优化效果。

图3 改进B-P模型对单调拉伸应力-应变曲线的模拟

图4 平均应力循环松弛曲线模拟

图5 稳态滞回环模拟(950 MPa)

图6 稳态滞回环模拟(850 MPa)

4 结 论

针对Bodner-Partom本构模型在模拟循环加载时精度有限、滞回曲线出现“过方”等缺陷，在其基础上提出了一种广义B-P黏塑性本构模型：①从塑性流动正交法则出发重塑了流动法则，摆脱了Mises法则的局限；②在运动硬化方程中引入黏塑性应变率修正项，拓展了描绘应变率效应的不同演化方向；③考虑了动态恢复的非线性特征，丰富了硬化准则的表达力。对FGH96材料高温非弹性变形特征的模拟以及试验验证表明，新模型相较B-P模型改善了模拟单调拉伸和循环硬化时的精度，初步获得了描述高温非对称循环载荷下平均应力松弛的能力，且证明了数值计算实践的可行性。