刷式密封摩擦热效应数值与实验研究
孙丹,李浩,赵欢,张国臣,李玉,冯毓钟
沈阳航空航天大学 航空发动机学院 辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136
刷式密封是具有优良密封性能的接触式动密封,转子高速转动时与刷丝束之间存在较大相对速度,产生大量摩擦热量,摩擦热通过热传导进入刷丝,使刷丝的力学性能降低,摩擦热效应问题直接影响刷式密封的封严性能与使用寿命。因此开展刷式密封摩擦热效应研究具有重要的理论意义与工程应用价值。
国内外学者对刷式密封摩擦热效应研究包括数值与实验研究。在数值研究方面,国外Hendricks等[1]首次提出刷式密封摩擦热流量的计算公式,Owen等[2]对刷式密封传热特性进行了理论分析,Dogu等[3-6]给定了刷丝与转子表面间的摩擦热量,数值预测了刷式密封的温度分布,采用改进非线性Darcian多孔介质模型,研究了不同密封间隙、不同后挡板结构参数下的刷式密封流场特性与泄漏流动特性以及不同压差、不同热流密度下刷式密封温度分布情况。Modi[7]采用悬臂梁模型,提出了单根刷丝自由端与转子面接触力的计算方法。国内陈春新等[8]采用线性悬臂梁建立了单根刷丝与转子的接触力模型,分析了刷丝安装角对刷丝自由端接触力的影响规律。马登骞[9]、刘璐园等[10]采用基于非线性Darcian多孔介质模型的三维RANS(Reynolds-Avergaed Navier-Stokes)方程耦合FEM(Finite Element Method)接触模型的数值方法,研究了刷丝直径、刷丝倾斜角和刷丝束与转子面干涉量对摩擦力的影响。孙丹等[11-12]采用了流固耦合方法研究刷式密封刷丝变形及接触力学特性,实验观测了刷丝运动轨迹变化过程,研究了刷丝的变形规律与力学特性,发现刷丝在气流力作用下会产生摆振运动,刷丝固定端应力随着刷丝摆振运动呈振荡变化。综上现有数值研究发现,刷式密封摩擦热效应多数基于摩擦热量理论公式获得摩擦热量,将其作为多孔介质模型边界条件进行热传导计算,缺乏刷丝与转子接触摩擦温度的数值研究,且未考虑刷式密封实际结构参数,难以准确模拟刷丝内部热量传递过程。
在实验研究方面,国外Hildebrandt等[13]通过实验对比分析了两种刷式密封实验件,发现刚度较大的刷丝在与转子摩擦时产生较高的摩擦热量。Huang等[14]数值模拟和实验测量了刷式密封的刷丝束尖端力和温度场。刷丝束最高温度出现在与转轴接触的刷丝束顶端,数值预测与试验的误差主要由摩擦系数和刷丝束几何结构参数等数值预测模型不够完善导致。Pekris等[15]对比分析了传统和压力平衡型刷式密封的封严性能、力学和传热特性。发现压力平衡型刷丝束与后夹板间的摩擦弱于传统型刷式密封。Demiroglu和Tichy[16]利用红外线温度测量仪和热成像照相机测得转轴和刷丝束保护高度区域温度分布。Raben等[17]对刷式密封开展了磨损和摩擦热效应实验研究,并实验观测了刷丝颤振现象,发现串列刷丝束结构可以良好适应转子的径向跳动。国内吴施志等[18]开展了刷式密封装置全工况条件下摩擦生热实验研究,引入了刚度修正系数,并对刚度修正系数进行了确定及验证。综上现有实验研究发现,以上研究多数基于热电偶对刷式密封尖端局部位置的温度值进行了采集,对刷式密封整体各向位置的温度分布进行热成像采集实验较少,鲜有对摩擦热导致的刷式密封温度分布研究,难以准确得出刷式密封整体摩擦生热的传热特性。
本文建立了基于三维实体建模的刷式密封刷丝-转子系统热固耦合数值模型,设计搭建了刷式密封柱面圆周摩擦热效应实验装置,利用热成像仪实验观测刷式密封传热过程,在实验验证刷丝-转子系统热固耦合模型准确性基础上研究刷式密封接触摩擦特性影响因素,数值研究了刷式密封摩擦热量传导引起的刷丝温度变化、刷丝热应力、刷丝接触变形,实验研究了刷式密封刷丝温度随干涉量、转速、刷丝束厚度等变化的影响规律,为刷式密封的结构设计提供理论依据。
1 刷式密封摩擦热效应理论分析
1.1 刷式密封热固耦合理论
1.1.1 刷式密封摩擦热传递过程
刷式密封属于接触式柔性动密封,工作运行过程中,在保证优良的密封效果时,同时会与转子表面接触摩擦产生大量摩擦热。摩擦热量在转子与刷丝尖端接触面分别传导进转子与刷丝束间,在二者间发生不同的热量传递过程,图1给出了刷式密封摩擦热量传递示意图,传热过程在图2中表示。
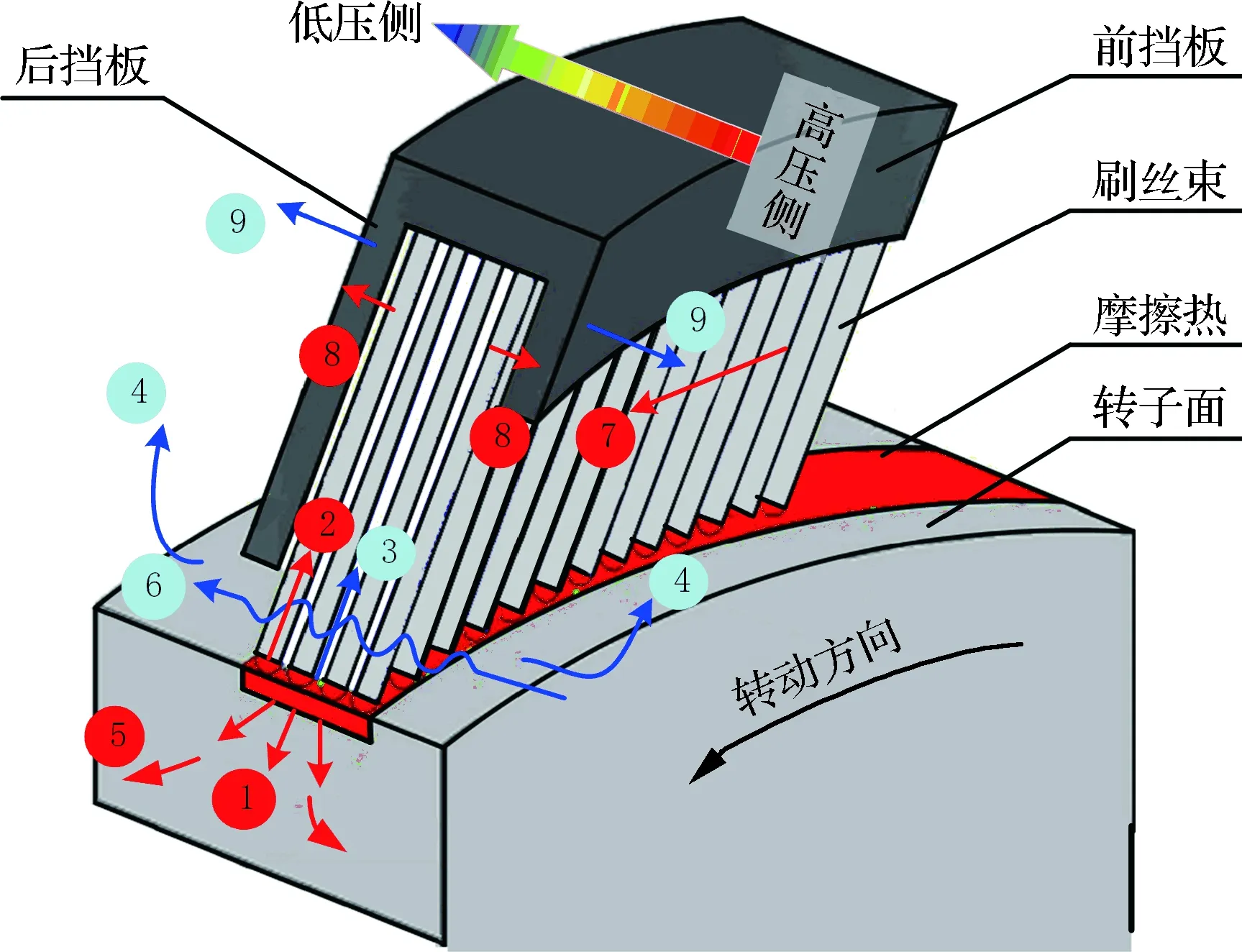
图1 刷式密封摩擦热量传递示意图
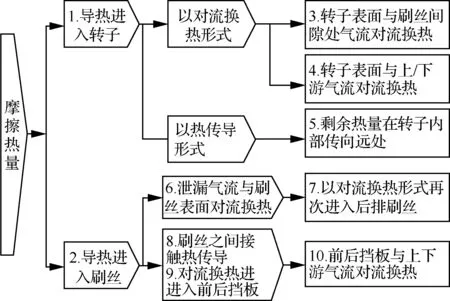
图2 刷式密封传热流程图
1.1.2 刷式密封热固耦合过程
刷式密封摩擦产生热量在刷丝-转子系统中传递,由于刷丝长径比很大,定义刷丝长度方向为“长轴方向”,由于泄漏气流在刷丝长轴方向上的速度梯度发生变化,刷丝与气流发生对流换热、与周围环境辐射换热,导致刷丝在长轴方向上产生温差,温差的出现使刷丝材料内部产生不同的热应力,导致刷丝产生热变形,刷丝变形后与转子间的接触状态发生改变,接触力发生改变,产生的摩擦热量也随之发生改变,热量在刷丝内部传导速度、路径等发生改变,又导致刷丝温度及热变形情况发生改变。正是这种摩擦热量与刷丝材料固体之间的相互作用,使刷丝的摩擦热效应呈现一个动态循环。
刷丝在转子跳动时跟随转子跳动,刷丝与转子间接触力使刷丝在转子径向方向长度发生变化,该应变为线应变。刷丝跟随转子跳动,刷丝内部产生机械应力以抵抗接触力带来的刷丝应变。由于刷丝柔性较大,刷丝内部抵抗转子偏心力的能力较低,其机械应变相对于转子偏心带来的变形更小。因此在刷式密封热固耦合刷丝-转子系统热固耦合计算流程中,未考虑刷式密封的机械力产生的应变。
热固耦合问题的基本方程涉及到热量在刷丝内部的热传导、刷丝材料受热变形。刷丝在长轴方向上的温度非均匀,对非均匀温度场下的热固耦合结构进行分析,温度场和结构场系统其理论控制方程表示为[19]
(1)
式中:Km和Kt分别表示结构的整体刚度矩阵和热刚度矩阵;T为刷丝固体的温度向量,u为结构的位移向量;Ft是加载在结构的热通量向量,Fm代表刷丝所承受的机械外载荷向量,在本文中具体表现为转子的偏心载荷,Fε是由于热应变产生的热载荷向量。
由文献可知结构受热膨胀引起的初始热应变ε0表示为[19]
ε0=αΔTΦT
(2)
式中:α为材料的热膨胀系数;ΔT为单元温度变化量;Φ为对应所建立模型下的空间向量,在二维建模情形下,Φ=[1,1,0],在三维模型问题中,向量Φ=[1,1,1,0,0,0]。对刷丝-转子系统热固耦合模型进行三维实体建模,是属于三维问题,因此在本文中向量Φ=[1,1,1,0,0,0]。
由温度场变化产生的热载荷向量Fε表示为
(3)
式中:i为单元序号,从第一个单元i=1开始;N为离散单元的数目;B为单元的应变矩阵;D0为弹性矩阵;Ω为i时的单元体积。假设材料为各向同性,平面应力问题的弹性矩阵具体形式为
(4)
式中:E为刷丝材料的弹性模量;μ为刷丝材料的泊松比。
1.2 刷丝传热控制方程
刷丝与转子摩擦时设定了转速、跳动等工况等随时间变化的瞬态设置,转子在不同时刻下的偏心转动带来了刷丝与转子之间的接触状态发生改变,因此可将刷式密封瞬态流固热耦合温度场可将其看作无数个连续准稳态温度场进行处理,用t表示计算过程中的时间段,n表示计算过程中的时刻,则在[tn,tn+1]时间段内流场准稳态温度控制方程为[20]
(5)

刷丝束固体区域准稳态导热方程为
(6)
式中:h为显焓;λ为刷丝材料的导热系数;T为刷丝材料温度;Q为摩擦热源。式(6)等号左边第1项表示刷丝能量随时间的变化,右边第1、2项分别表示传导引起的热流以及刷丝尖端的摩擦热源。
刷丝与转子摩擦产生的热量通过刷丝内部及相互间传导,同时又被上游高压来流气体所带至下游低压区域,需要确定刷丝与泄漏气流间的表面换热系数。刷丝相互交叉排列在泄漏流动气流中,可将其考虑为流体横掠叉排管束的流动模型,可确定出流体与刷丝表面间换热系数hfs[21]:
(7)
式中:Nud为刷丝表面的努赛尔数;η为流体动力黏度;λf为流体的导热系数;d为刷丝的直径;C2为叉排管束修正系数;C1为根据雷诺数和管束排列方式选取修正系数;Pr是管束进出口流体平均速度来确定的普朗特数;Prs是根据管束平均表面温度所确定的普朗特数;Red,max是根据叉排管束中最小截面处的最大流速所确定的雷诺数。
1.3 刷丝热变形控制方程
1.3.1 热变形原理
热变形原理相当复杂,在刷式密封的应用中,刷丝材料热膨胀参数以实测的热膨胀系数来表示。在工程实际应用中,对刷丝材料进行热变形计算时,多采用式演化而来的计算式[22]:
L2=L1+αL0ΔT
(8)
式中:L0为刷丝初始长度;L2与L1分别为刷丝温度T2与T1下的试样长度,二者之差可表述为该温差下的热变形之差,ΔT为温度T1至温度T2的增量。
1.3.2 热量引起刷丝热变形控制方程
刷丝端部与转子摩擦生成热量在刷丝内部进行热传导,热量的输入引起刷丝的变形。由式(8)可知,热变形与材料的热膨胀系数、温度等参数密切相关。升高单位温度时单位刷丝材料能量的增量称为刷丝材料的热容,其表达为[22]
CV=W/ΔTΔV
(9)
式中:CV为等容热容;W为能量增量;ΔV为刷丝材料容积增量。
格律乃森由晶格振动理论导出的刷丝材料体膨胀系数与热容之间的关系式为
(10)
式中:β为材料体膨胀系数;γ为格律乃森常数;K为体积模量;V为试样体积。
由此可得:
CV=KVβ/γ
(11)
摩擦热源对刷丝材料加热达到热平衡时,刷丝内所含热量相同,若采用刷丝材料的平均线膨胀系数αm来计算热膨胀量,则有:
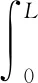
(12)
式中:f(x)为关于刷丝长度的刷丝材料温度分布函数;ΔL为材料伸长量。刷丝材料内部热容相同,由CV=W/ΔTΔV可得刷丝材料微元内的能量增量为
dW=CVf(x)πr2dx
(13)
则整根刷丝的能量增量为
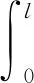
(14)
式中:r为刷丝端面半径。
由此可知,对于刷丝束,当摩擦热源位置不同时,工件内的温度分布将呈不同状态。只要刷式密封工作条件相同,当刷式密封达到热平衡时所吸收的能量必然相同,此时采用平均线膨胀系数计算得到的工件热膨胀值相等。在刷式密封实际工程应用中,刷式密封的温度分布函数较复杂,不便于计算,可将其变换为热量含量相同且温度均布的状况进行计算,这样可大幅度减少计算量且可保证计算精度。
图3所示为刷式密封刷丝与热量间的耦合流程图。刷式密封热固耦合计算流程中tn时刻和tn+1时刻表示在所设置的热固耦合瞬态计算总时长中的某一计算时刻及其下一时刻,设定热固耦合计算总时长,在该时长内设定计算步,图3中的tn到tn+1时间段为总计算时长的一个很小的时间段,[tn,tn+1]计算时长较短,在该时间段内的转子偏心转动带来的摩擦热量以及热传递可看作稳态过程。每一次计算步都会得到一个迭代计算的值,在该计算步上得到所迭代的节点温度值,将此时得到的节点温度值代入下一个计算步进行再一次迭代计算,得到新的节点温度值,在判断收敛时的将两个计算步所得到的节点温度值进行残差计算,如果其残差小于所设定的残差值,认为其收敛,否则将进行下一个计算步的迭代计算。

图3 刷式密封刷丝-转子系统热固耦合流程
2 刷式密封摩擦热效应实验
2.1 实验装置
设计搭建了基于柱面圆周摩擦形式的刷式密封摩擦热效应实验装置。如图4(a)和图4(b)所示,分别为该实验装置的主视图、俯视图、刷式密封三向可调刷式密封安装座。该实验装置以一矩形铸铁方箱为基础构建并竖直放置于水平实验台上,实验装置的动力由一台伺服电机提供,其最大转速为5 000 r/min。伺服电机通过扭矩传感器(量程范围:0~20 N·m)与主轴联结,扭矩传感器的作用是测量实验过程中的摩擦力扭矩。在主轴顶端是一最小直径360 mm的摩擦转盘(阶梯盘),该摩擦转盘设置10个阶梯,相邻阶梯之间半径相差0.1 mm,该摩擦转盘的作用是提供刷式密封实验件所需的不同干涉量,干涉量可在0~1.0 mm范围内调整。刷式密封实验件通过一带有特制凹槽的夹具安装在三向可调刷式密封安装座上,该安装座包括两个拉压力传感器(量程范围:0~50 kg),用于测量刷式密封实验件与转子间的x轴径向正压力与y轴转子表面切向摩擦力。在阶梯盘正上方将红外热像仪热成像仪利用相机架固定,红外热成像仪具有调焦、可人为设定检测范围以及调定红外成像范围的功能。通过调定焦距、范围等参数监测不同工况下的刷式密封摩擦热效应热成像图。红外热像仪可实时采集刷式密封摩擦磨损过程中的热成像,将刷丝温度在不同时刻、不同干涉量下记录并保存,在电脑中可对保存数据进行后处理。

图4 刷式密封摩擦热效应实验装置
图4(c)给出了刷式密封摩擦热效应实验装置三向可调刷式密封安装座示意图。刷式密封实验件装在密封实验件夹具上,而刷式密封夹具又安装在三向可调刷式密封安装座上,该安装座可使得刷式密封实验件的位置在3个方向上进行调节。实验时,首先通过密封实验件夹具将刷式密封实验件固定,之后通过调节x轴径向滑竿、y轴转子表面切向滑竿、z轴方向滑座使得刷式密封实验件可以与阶梯盘的不同阶梯相接触,进而使刷式密封实验件与阶梯盘间产生实验所需的的不同干涉量,最后启动伺服电机,记录扭矩传感器和拉压力传感器的数据。同时对拉压力传感器测量得到的刷丝与转子间正压力和摩擦力,采用拉压力传感器测得的摩擦力计算刷式密封摩擦系数。表1给出了基于刷式密封摩擦热效应实验装置采集刷丝温度分布的实验工况。

表1 刷式密封摩擦热效应实验工况
2.2 刷式密封实验件
设计加工了刷式密封实验件,如图5所示。实验件刷丝材料为Haynes 25,弹性模量为213.7 GPa,泊松比0.29。对刷式密封进行整周45°截取所得实验件,刷式密封在周向方向上具有周向循环特性,利用45°扇形段可以在周向方向上循环对称可以得到整环刷式密封的摩擦热效应温度分布特性图,且便于热成像仪对焦,有利于更加清晰的捕捉刷丝运动变形的情况,故将实际刷式密封简化为45°扇形段结构进行研究。同时为了降低试验所带来的误差,对所有实验均进行3次数据采集并通过3次所采集的数据取平均值。实验件安装位设计成T型槽结构,可与安装基座上的T形槽配合并通过螺栓顶紧使其稳定固定于安装基座上。刷式密封实验件主要参数如表2所示。

图5 刷式密封实验件
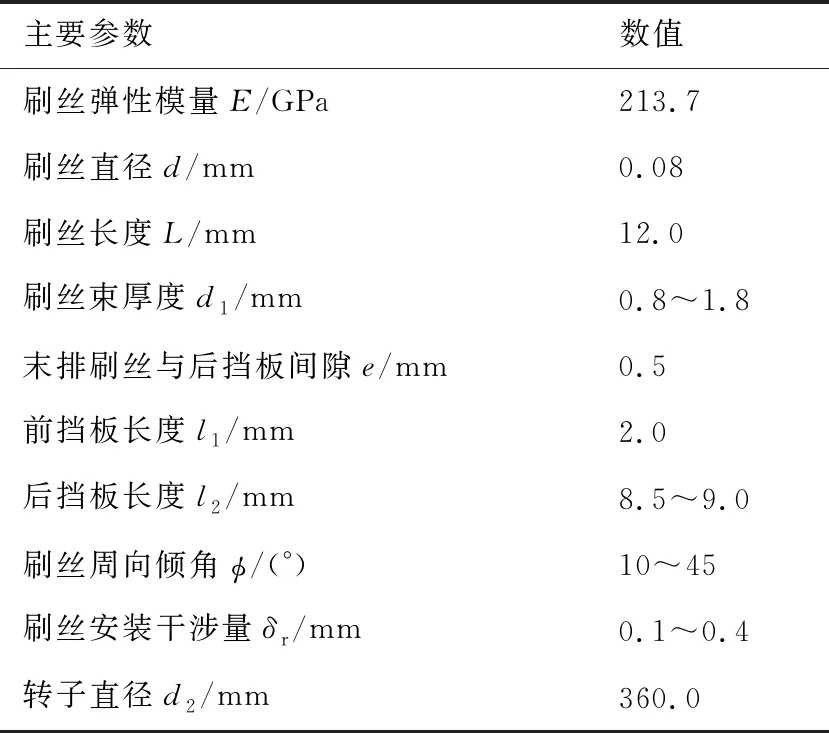
表2 刷式密封主要结构参数
2.3 实验结果分析
2.3.1 刷丝束厚度对摩擦热效应影响
图6给出了刷式密封在刷丝束厚度为1.8 mm,干涉量为0.4 mm,后挡板长度为8.8 mm,刷丝安装角为45°时在不同转速下的温度热成像图。由图6可以看出,在低转速时,刷丝与转子产生的摩擦热量较少,摩擦热量在刷丝中传导能力较小,导致刷丝尖端温度较高,但在刷丝中部温度依然较低,随着转速的上升,线速度增大,摩擦热量也增大,刷丝中传导的热量增大,刷丝中部以及固定端部位置的温度均随着转速的上升而上升,但最高温度依然集中在刷丝尖端部分。由图6还可以看出刷丝束最高温度的位置发生了变化,这是由于在摩擦过程中,由于刷丝束磨损情况发生变化,导致刷丝与转子间接触力发生变化,最高温度出现位置也随之发生变化。
图7给出了在不同转速下的刷式密封干涉量为0.4 mm,后挡板长度为8.8 mm,刷丝安装角为45°时最高温度随刷丝束厚度变化曲线图。由图7可以看出,1.8 mm厚度刷式密封最高温度是在2 000 r/min时的136.0 ℃,1.2 mm厚度刷式密封最高温度是在2 000 r/min时的110.0 ℃,0.8 mm厚度刷式密封最高温度是在2 000 r/min时的98.6 ℃。由图7还可以看出在低转速下,三种刷丝束厚度的温度相差不大,这是由于低转速时产生的摩擦热量较少,同时由于空气具有黏性,转子转动时会带起气流跟随转动,气流对刷丝束起到冷却作用,所以此时温度相差不大。但转速越大,摩擦热量越大,在本文刷式密封研究的干涉量工况下,转子转动带起的气流冷却效果小于摩擦热的产生。因此,刷丝束厚度越大,接触面积越大,同转速下产生的摩擦热量越大,最高温度差值随之增大。在设计过程中,可适量考虑刷丝束厚度,使其达到既能保证泄漏量的同时,也使刷丝束温度不至于过高,保证刷丝的寿命稳定在可靠范围。
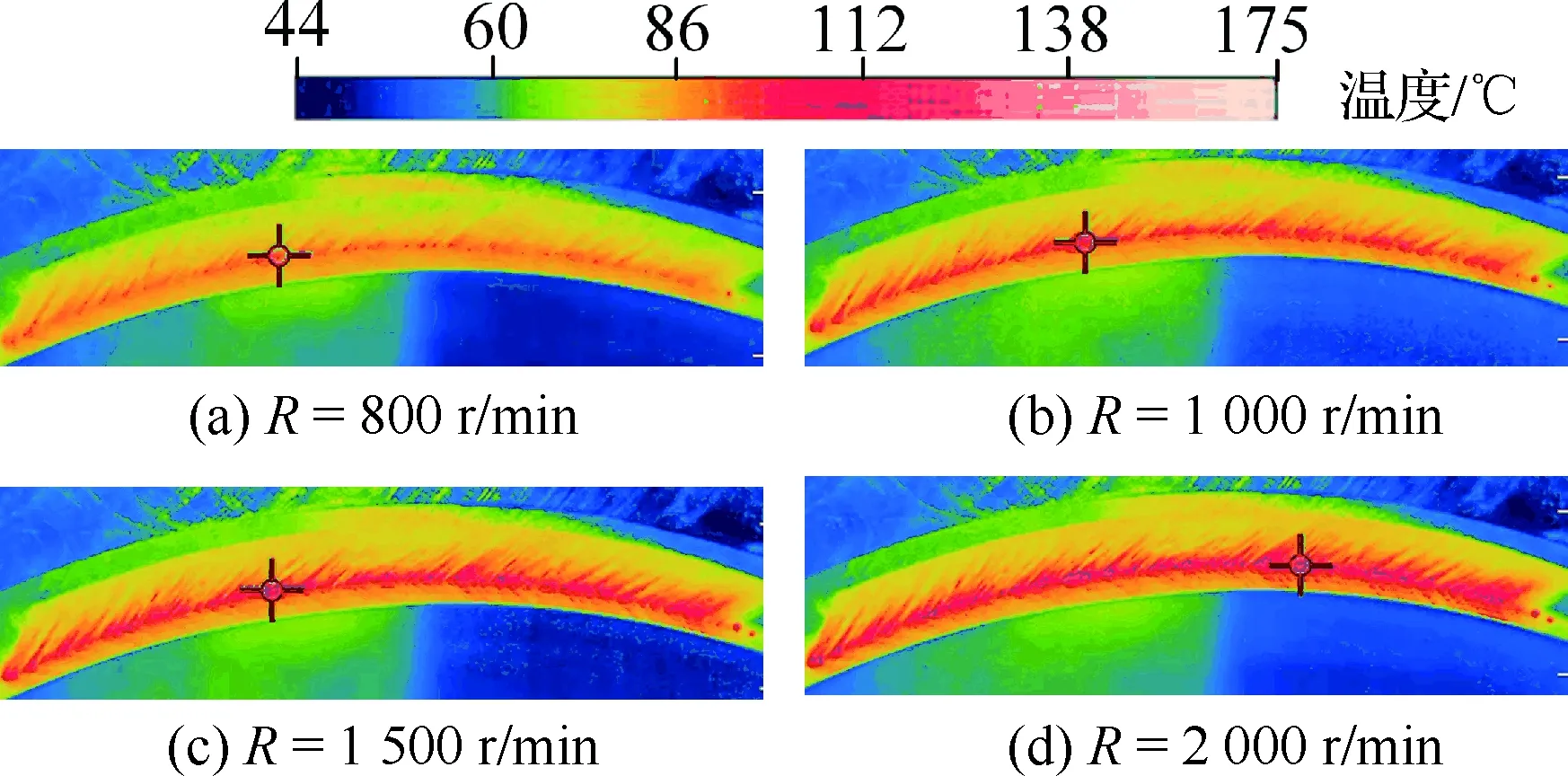
图6 刷式密封温度热成像图(d1=1.8 mm)
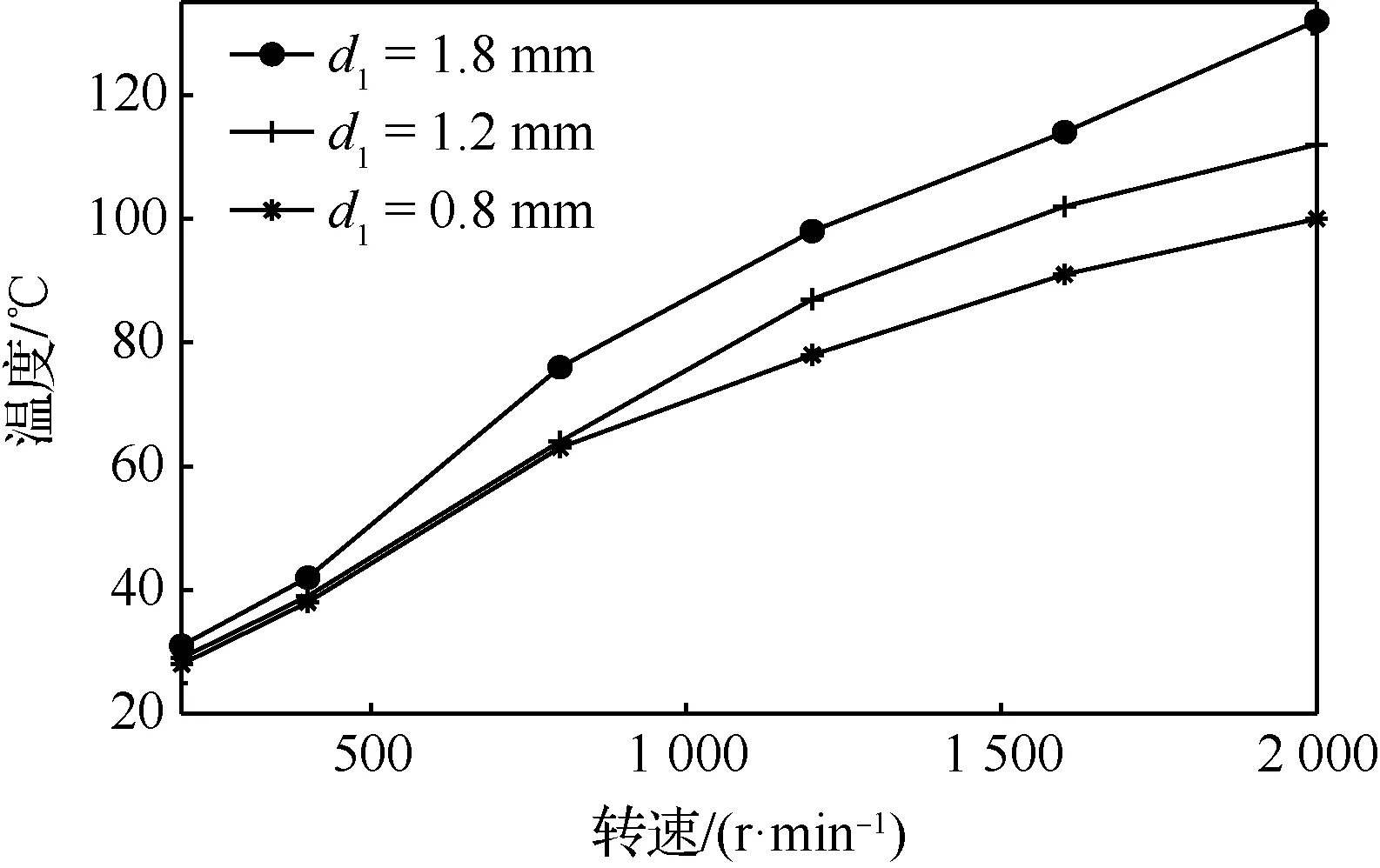
图7 刷式密封最高温度随刷丝束厚度变化曲线
2.3.2 后挡板长度对摩擦热效应影响
图8给出了刷丝密封在干涉量为0.4 mm、刷丝束厚度为1.8 mm、刷丝安装角为45°、不同转速下的刷式密封最高温度随后挡板长度的变化曲线图,由图8中可以看出,不同后挡板长度的刷式密封最高温度之间差值随着转速增大而增大,在较低转速时,3种后挡板长度的刷式密封最高温度值接近。随着刷式密封后挡板长度的减小,最高温度值降低,这是由于后挡板长度越小,刷丝裸露面积越大,热量在刷丝束内部的积累越少,使得最高温度随着后挡板长度的减小而降低。

图8 刷式密封最高温度随后挡板长度变化曲线
2.3.3 摩擦时长对摩擦热效应影响
图9给出了刷式密封在转速为2 000 r/min、干涉量为0.4 mm、刷丝束厚度为1.8 mm、后挡板长度为9.0 mm、刷丝安装角为35°、室温为31.0 ℃的工况下温度随摩擦时长变化曲线图,从图中可以看出,2.0 min时刻刷丝束温度为45.1 ℃,6.0 min时刻温度为79.4 ℃,在18.8 min时刻达到了最高温度164.0 ℃,从室温升高到164.0 ℃过程用了18.8 min,到达最高温度值164.0 ℃后温度开始逐渐下降,但相较于温度升高的过程,下降的趋势逐渐减缓,这是由于在初始阶段,刷丝束与转子过盈量较大,接触力较大,转子转动后在短时间内温度升高速率较大,当达到最高温度值后,此刻对应0.4 mm干涉量下的温度状况,随着时间的增长,刷丝束与转子摩擦,刷丝尖端被磨损,与转子干涉量逐渐减小,温度逐渐降低。

图9 刷式密封温度随摩擦时长变化曲线
由图9还可以看出,在0.5 h时之前,刷式密封温度变化速率较大,温度在18.8 min时刻达到164.0 ℃,然后下降至140.0 ℃开始变得平缓,随后又开始上升,这是由于在摩擦过程中,刷丝在摩擦力作用下出现刷丝刚化效应,刷丝刚度变大,刷丝与转子接触力增大,导致摩擦热量增大,温度又开始上升。随着摩擦时长增大,刷丝磨损量增大,接触力减小,温度逐渐降低。刷式密封在1.0 h之内出现较大磨损量,1.0 h后刷丝已被大量磨损,刷丝与转子的接触力大大减小,1.0~4.5 h间,温度从1.0 h的114.0 ℃降至4.5 h的51.0 ℃,该过程近似为线性降低。在4.5~6.0 h间,温度稳定在50.0 ℃左右,可以推断出此时刷丝束与转子磨损量很小,温度变化量较小。
2.3.4 干涉量对摩擦热效应影响
图10给出了刷式密封在转速为2 000 r/min、刷丝束厚度为1.8 mm、后挡板长度为9.0 mm、刷丝安装角为35°、室温为31.0 ℃的工况下刷式密封温度在不同干涉量下的变化曲线图,从图中可以看出,0.4 mm干涉量刷式密封最高温度为164.0 ℃,0.3 mm干涉量刷式密封最高温度为105.3 ℃,这是由于刷丝与转子干涉量不同,转子转动时刷丝接触力不同,导致产生的摩擦热量不同。
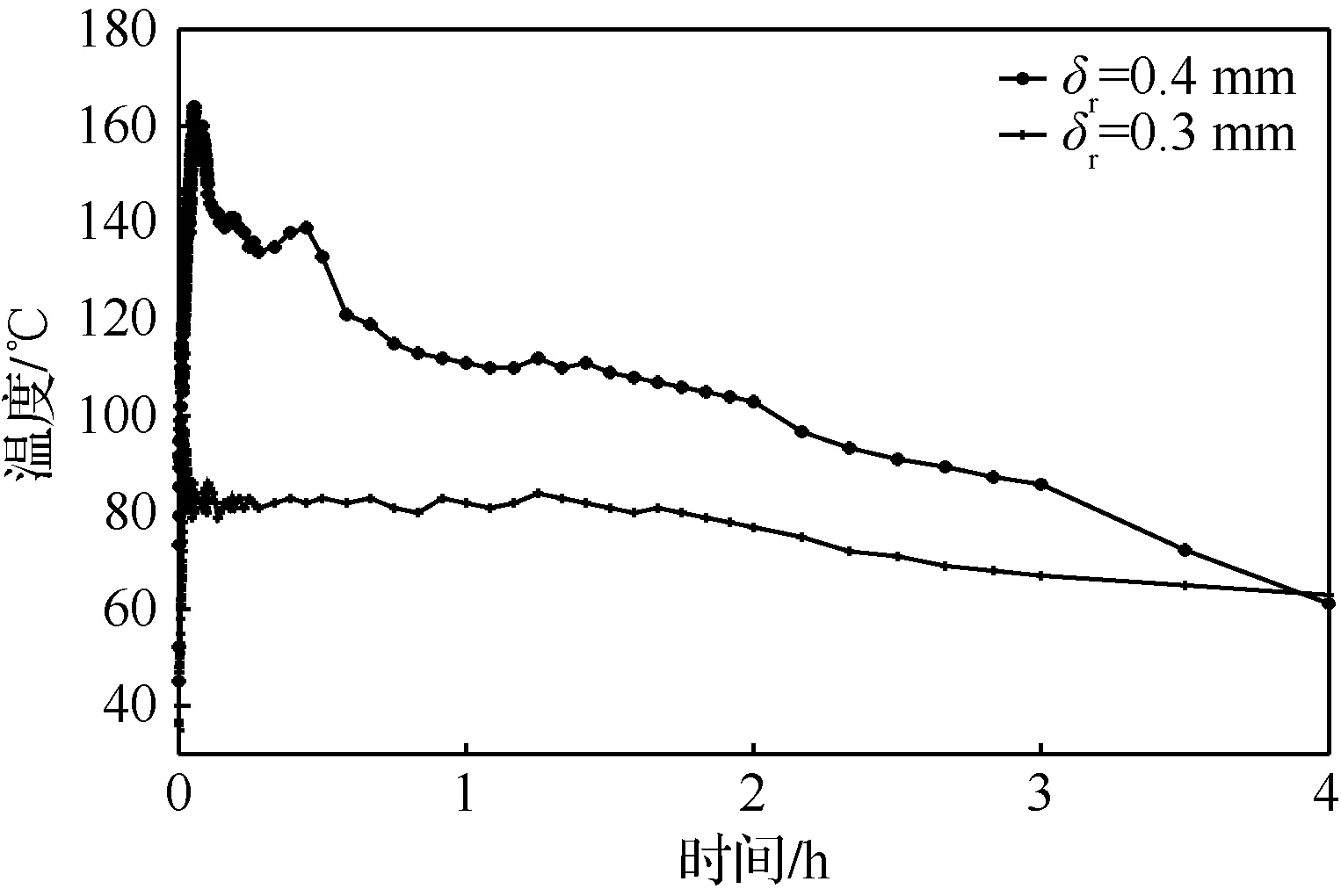
图10 刷式密封温度随干涉量变化曲线
由图10还可以看出,两种干涉量的密封达到最高温度后,均在较短时间内开始下降,其最高温度在2.0 h后稳定在某一个范围,这是由于刷式密封在与转子摩擦过程中,刷丝束被磨损,刷丝尖端接触面由于磨损使的磨损面变得更为光滑,摩擦系数降低,进而使得温度提升不高。但0.4 mm干涉量相较于0.3 mm干涉量同一时刻下温度更高,这是由于干涉量越大,刷丝被磨损越多,刷丝长度减小,刷丝刚度增大,接触力更大,所以同时刻下的0.4 mm干涉量刷式密封温度更高。干涉量越大,刷丝与转子间接触更紧密,能在相同情况下保持更优良的密封性能,但是同时所产生的摩擦热量也越大,磨损也更快,因此干涉量大小影响着刷式密封的使用寿命和封严性能,选择合适的干涉量即能保持良好的密封效果,也能保证使用寿命在可接受范围,在刷式密封设计参数中干涉量需要重点考虑。
3 刷式密封摩擦热效应数值研究
3.1 数值模型及边界条件
根据刷式密封摩擦热效应实验装置实验段建立基于三维实体模型的刷式密封刷丝-转子系统接触热固耦合模型。由于刷丝是长径比很大的结构,且整周刷丝数量较多,刷式密封刷丝之间、刷丝与挡板、刷丝与转子同属于多体接触,计算较为复杂困难,为提高刷式密封热固耦合瞬态分析计算效率,建立由20根刷丝组成的单排刷丝模型,刷丝安装角从10°~45°不等,根据实验装置建立转子、耐磨涂层带、前挡板及后挡板实体模型。
在数值计算过程中,对刷丝单元采用C3D8RT单元进行计算,该单元是具有8节点控制的缩减积分单元,能够获得三维线性位移和温度,控制三维实体模型下的刷丝模型进行热-位移耦合计算,减缩积分单元对位移的求解结果较精确,在弯曲载荷下不容易发生剪切自锁,网格的扭曲变形对其分析精度影响不大,同时对该单元采取ALE(Arbitrary Lagrange Euler)自适应网格属性,可自适应刷丝在热量传导下的变形情况。图11所示为刷式密封刷丝-转子系统实验段局部示意图。表3给出了刷式密封热固耦合边界条件。
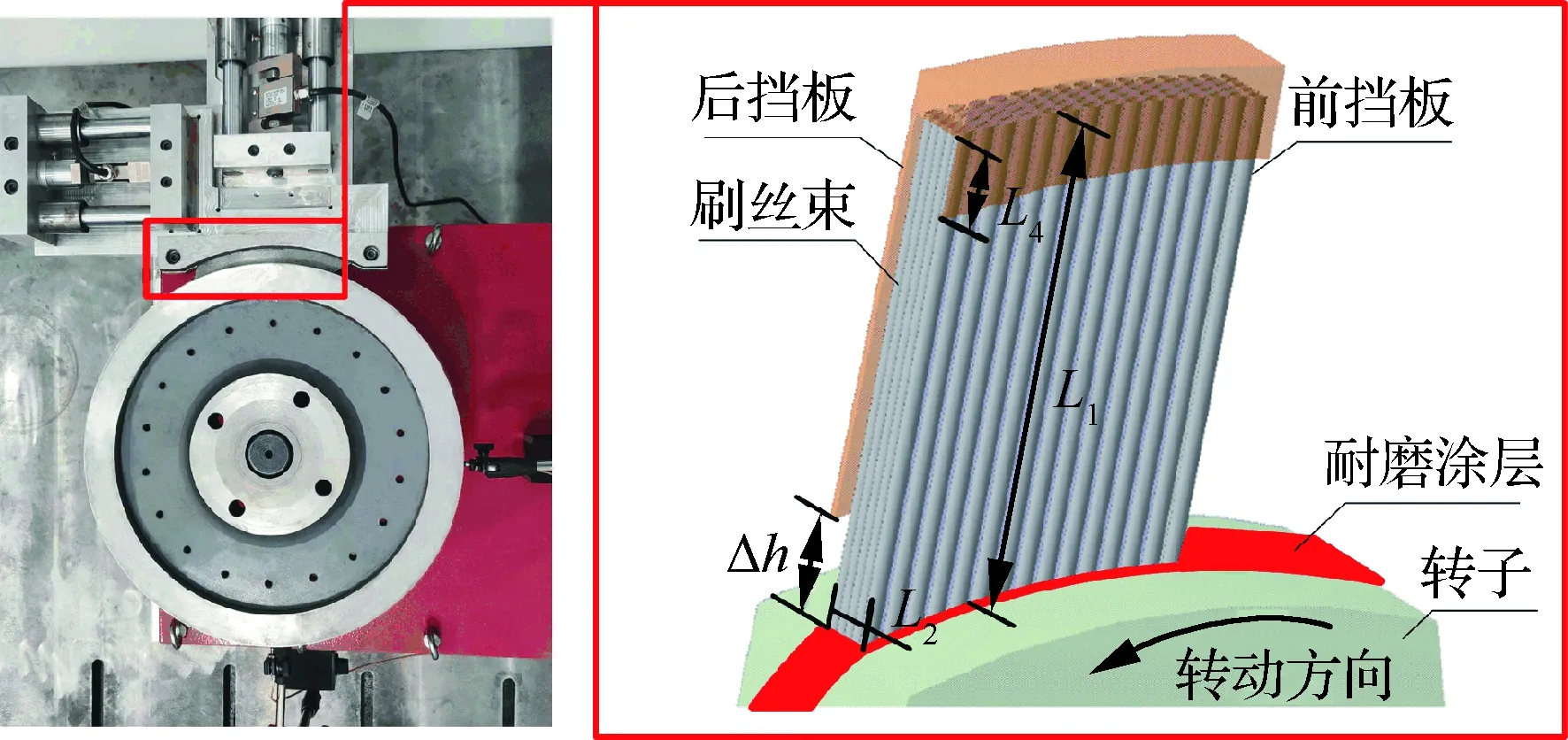
图11 刷式密封刷丝-转子系统实验段局部示意图
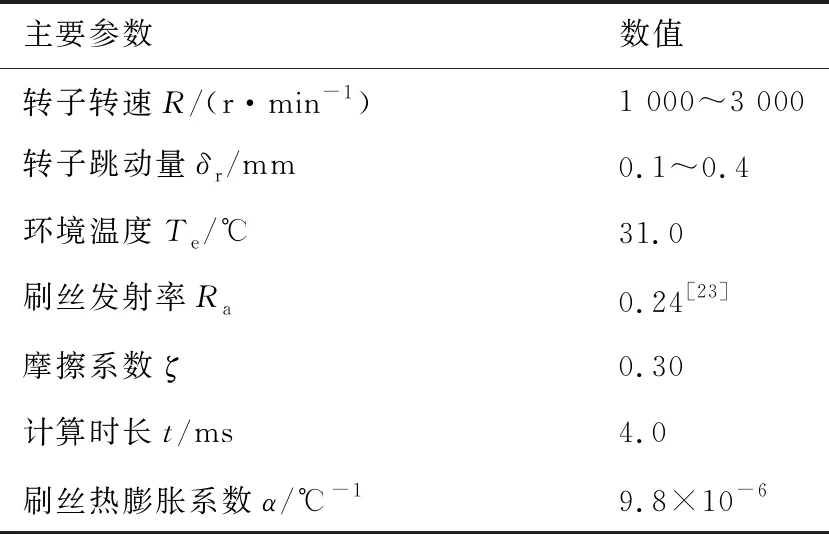
表3 刷式密封热固耦合模型边界条件
3.2 刷式密封热固耦合数值方法
刷式密封刷丝-转子系统热固耦合过程如下。首先是刷丝与转子间产生接触力,从而产生热量。其次产生热量在刷丝-转子系统中传递,刷丝在长轴方向上产生温差。温差的出现使刷丝材料内部产生不同的热应力,导致刷丝产生热变形,刷丝变形后与转子间的接触状态发生改变,接触力发生改变,产生的摩擦热量也随之发生改变。正是这种摩擦热量与刷丝材料固体之间的相互作用,使刷丝的摩擦热效应呈现动态循环。通过数值计算刷式密封热固耦合过程,在该过程中涉及到刷式密封热固耦合模型结构场与温度场控制方程,刷丝与转子接触理论控制方程,热量在刷丝内热传导控制方程,热量引起刷丝热变形控制方程,上述理论控制方程与刷式密封刷丝-转子系统热固耦合计算密切联系。图12为刷式密封热固耦合过程图。
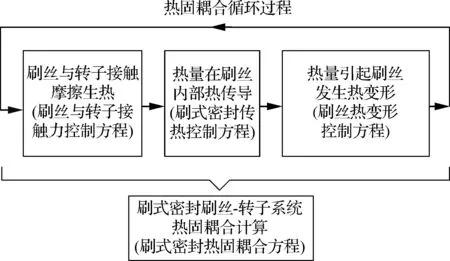
图12 刷式密封热固耦合过程图
3.3 刷丝-转子系统热固耦合模型准确性验证
图13给出了利用红外热成像仪采集测量刷丝束厚度为1.8 mm、后挡板长度为9.0 mm、干涉量为0.4 mm、刷丝安装角为45°刷式密封在不同转速下的温度分布及最高温度值。图14给出了刷式密封在刷丝束厚度为1.8 mm、后挡板长度为9.0 mm、刷丝安装角为45°,干涉量为0.4 mm下转速变化时最高温度数值计算与实验测量对比图。从图14中可以看出,数值计算与实验测量均随转子转速的增大而增大。数值计算值在转速较低时温度高于实验测量值,这是由于在实验过程中,转子转动带动周围气体流动,气流速度带走了刷丝与转子摩擦产生的较多热量,使得实验测量值偏低,而在转速上升至3 000 r/min时,此时的实验测量值高于数值计算值,这是由于在实验过程中,产生摩擦热量的一部分存储在刷式密封-转子系统中,随着时间的增长以及转速的提高,摩擦热量累积越来越多,使得实验温度测量值高于数值计算值。
从图14中还可以看出,数值计算值与实验测量值得最小误差集中在转速为1 400 r/min左右,此时的误差最小为0.6%,最大误差为17.9%,这主要是由于刷式密封结构过于复杂,数值计算采用的模型与实际刷式密封之间存在误差,三维实体模型的部分简化是造成数值计算与实验测量之间误差存在的主要原因,数值计算与实验测量的平均误差为8.9%,误差在可接受范围内,因此刷丝-转子系统热固耦合模型具有较高的准确性。

图13 刷式密封不同转速下热成像温度分布及最高温度值

图14 刷式密封最高温度数值计算值与实验测量值对比
3.4 数值结果分析
3.4.1 刷式密封刷丝应力分布结果
图15给出了刷式密封刷丝在安装角为10°,转速为2 000 r/min,干涉量为0.4 mm,刷丝束厚度为1.8 mm、后挡板长度为9.0 mm时的应力分布。从图15中可以看出,1.6 ms时刻,应力变化集中在刷丝束的中部偏上位置,2.4 ms时刻,刷丝束由于收到转子跳动而产生接触变形,应力变化集中在固定端和自由端,随着转子的继续扰动,4.0 ms时刻转子偏心转动达到最大值,刷丝出现无规则接触变形,刷丝各部分均出现较大的应力变化。刷丝最大应力为680.56 MPa,出现在刷丝固定端,沿着刷丝径向向下,应力逐渐减小,这是由于刷丝在随着转子跳动时,刷丝自由端变形较大,而在固定端的变形量接近为0 mm,刷丝变形量的差值引起刷丝内部产生应力,刷丝变形量越大,固定端与自由端变形量相差越大,则应力越大。
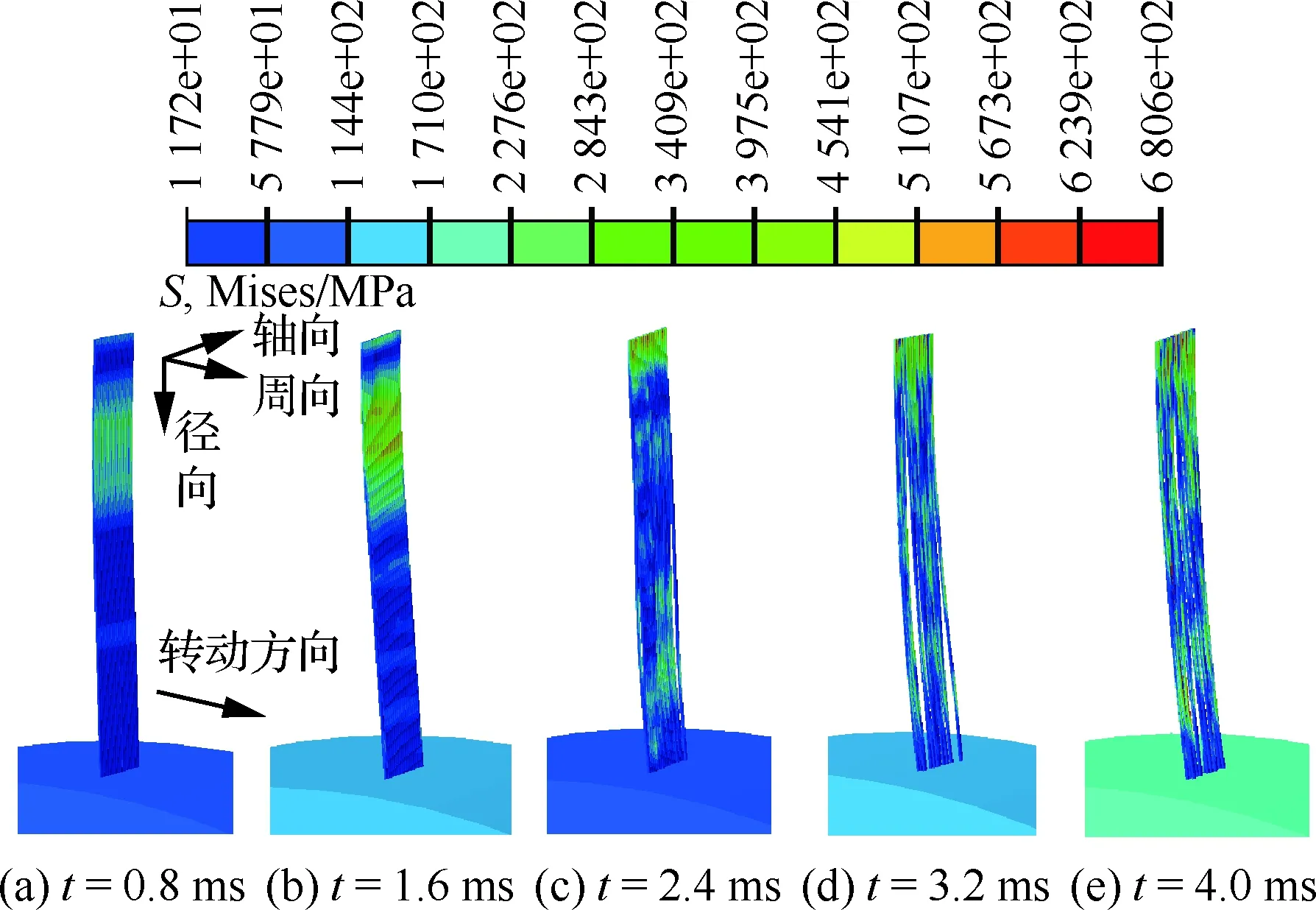
图15 刷式密封刷丝应力分布
3.4.2 刷丝与转子接触变形结果
图16给出了刷式密封刷丝在安装角为10°,转速为2 000 r/min,干涉量为0.4 mm,刷丝束厚度为1.8 mm、后挡板长度为9.0 mm时的刷式密封刷丝接触变形图。从图16中可以看出,1.6 ms时刻,此时转子偏心转动量较小,刷丝接触变形受转子影响较小,此刻变形量为0.508 mm,在2.4 ms时刻刷丝自由端变形量增大,在4.0 ms时刻自由端变形量达到最大值,刷丝与转子接触变形最大为1.524 mm,出现在中排刷丝的自由端,这是由于前排刷丝与后排刷丝在随转子跳动时,将自身所带能量传至中排刷丝,导致中排刷丝中某根刷丝受到压应力较大,增大了刷丝与转子之间的接触力。
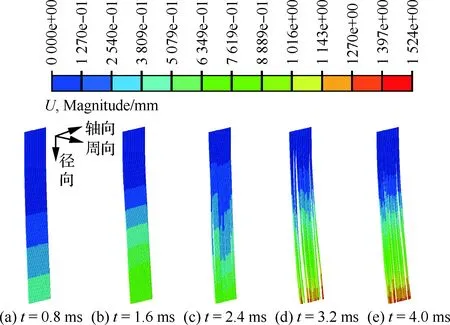
图16 刷式密封刷丝接触变形
3.4.3 刷式密封刷丝温度分布结果
图17给出了刷式密封刷丝在安装角为10°,转速为2 000 r/min,干涉量为0.4 mm,刷丝束厚度为1.8 mm、后挡板长度为9.0 mm时的温度分布。由图17中可以看出,刷丝温度最高为538.6 ℃,出现在刷丝自由端,且由于每根刷丝与转子接触力不同,每根刷丝最高温度均不同,这是由于转子发生跳动时,刷丝跟随转子跳动,由于刷丝自身柔性较大,刷丝与刷丝之间发生碰撞,某些刷丝受到相近刷丝干扰,导致了刷丝束并没有发生同步跳动,与转子之间接触力不同,摩擦热量不同,最高温度便出现差异。

图17 刷式密封刷丝温度分布特性
3.4.4 刷丝安装角对刷丝束最高温度的影响
图18给出了刷式密封在2 000 r/min,干涉量为0.4 mm,后挡板长度为9.0 mm,刷丝束厚度为1.8 mm下最高温度随刷丝安装角的变化曲线图,从图18中可以看出,最大温度值为538.6 ℃时,对应的刷丝安装角为10°,最小温度值为136.0 ℃时,对应的刷丝安装角为45°,随着刷丝安装角的逐渐增大,刷丝最高温度逐渐下降,且下降趋势逐渐减缓,刷丝安装角越大,接触力越小,因此最高温度也越低。因此,在刷式密封设计时,为保证刷丝力学性能保持在相对稳定范围,减小由于安装角过小带来的摩擦温升对刷丝力学性能影响,刷丝安装角设计越大越好,但刷丝安装角同时要采用适当角度,这是由于刷丝安装角越大,刷丝切斜角度过大,刷丝圆周面与转子接触,导致接触面积增大大,刷丝与转子由点接触变为面接触,转子高速转动下会使刷丝磨损增大。
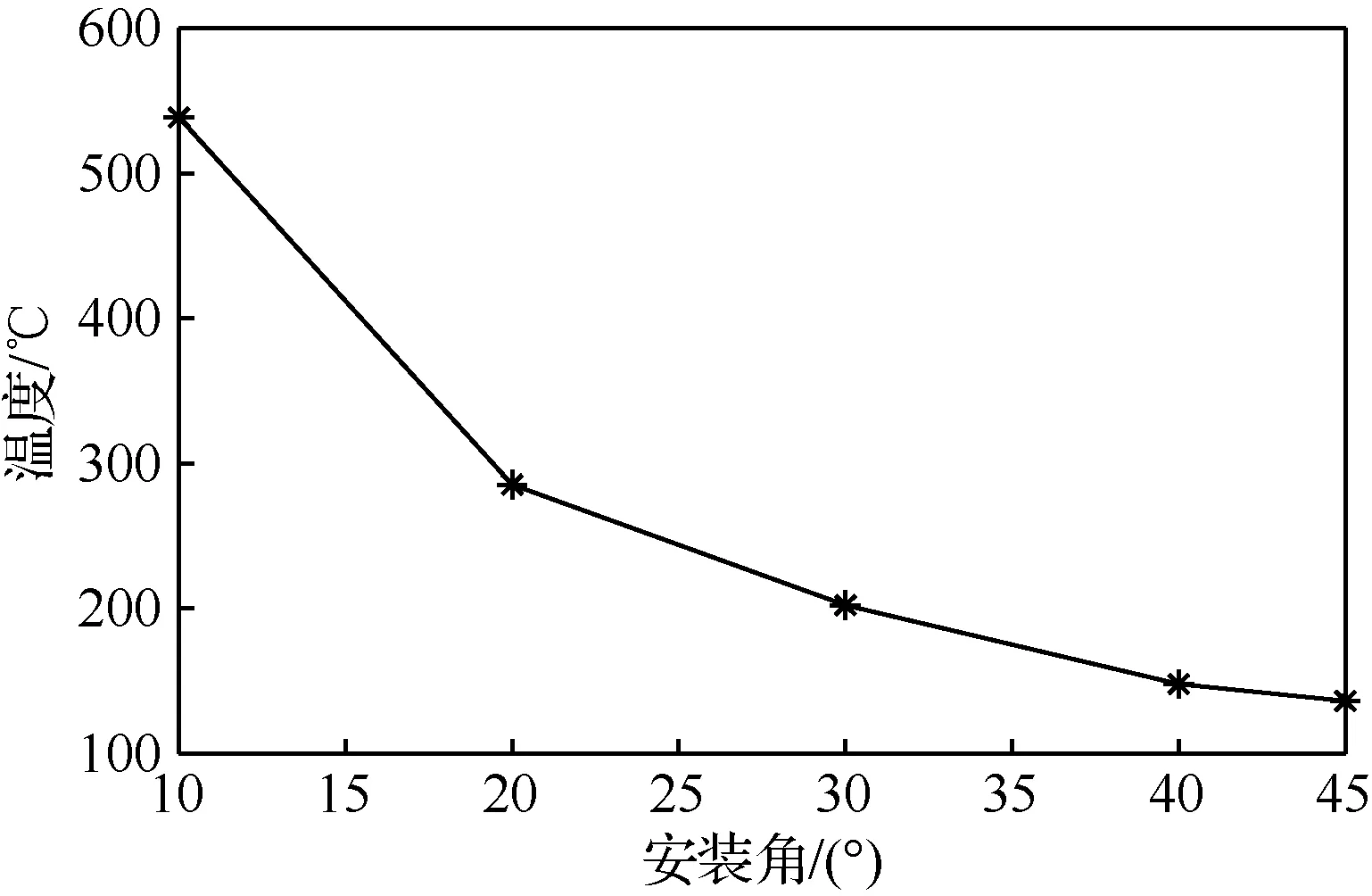
图18 刷式密封最高温度随刷丝安装角变化曲线
3.4.5 转速对刷丝束最高温度的影响
图19给出了刷式密封刷丝在干涉量为0.4mm,刷丝安装角为45°、后挡板长度为9.0 mm,刷丝束厚度为1.8 mm下最高温度随转速的变化曲线图。从图19中可以看出,转速为3 000 r/min时最大温度值为197.3 ℃,转速为600 r/min时最高温度值为46.1 ℃,3 000 r/min时的最高温度相较于600 r/min升高了4.3倍,最高温度随转速的增大而增大,这是由于转速增大后,跳动的转子与刷丝以更高频率接触,刷丝跟随转子跳动频率增大,产生的摩擦热量增大,温度上升加快。
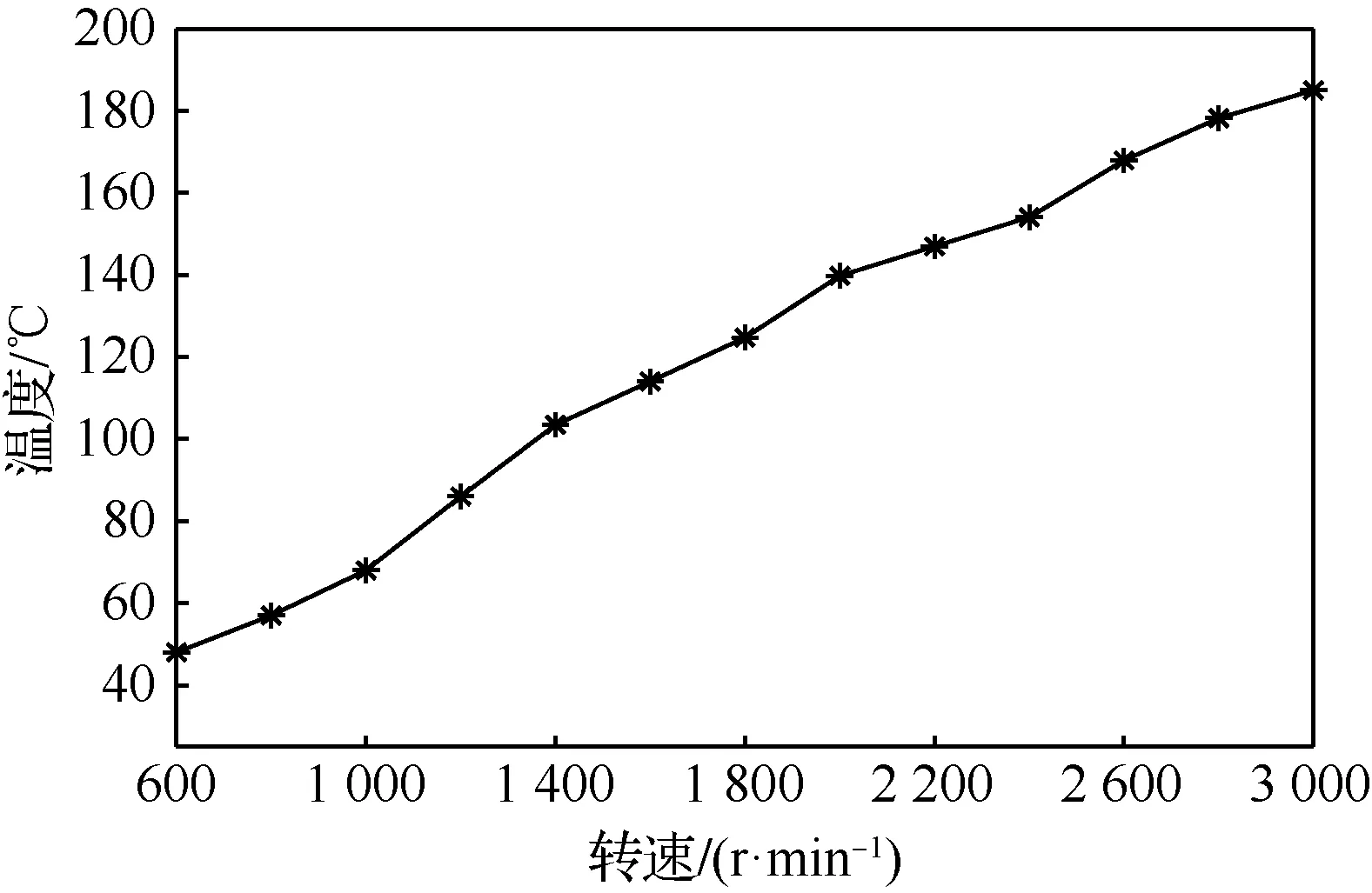
图19 刷式密封最高温度随转速变化曲线
3.4.6 干涉量对刷丝束最高温度的影响
图20给出了刷式密封刷丝在刷丝安装角为45°,转速为2 000 r/min,后挡板长度为9.0 mm,刷丝束厚度为1.8 mm下最高温度随干涉量的变化曲线图。从图20中可以看出,随着干涉量逐渐增大,温度也随之逐渐增大,在本文研究的工况下最高温度从58.0 ℃上升到了136.0 ℃,提高了1.34倍。这主要是由于随干涉量的增加,刷丝与转子的接触力增加,产生的摩擦热量增加,导致最高温度增加。因此在实际工作中,应当合理的选择干涉量,防止出现刷丝温度过高,刷丝磨损严重等现象,从而大大降低其密封性能。
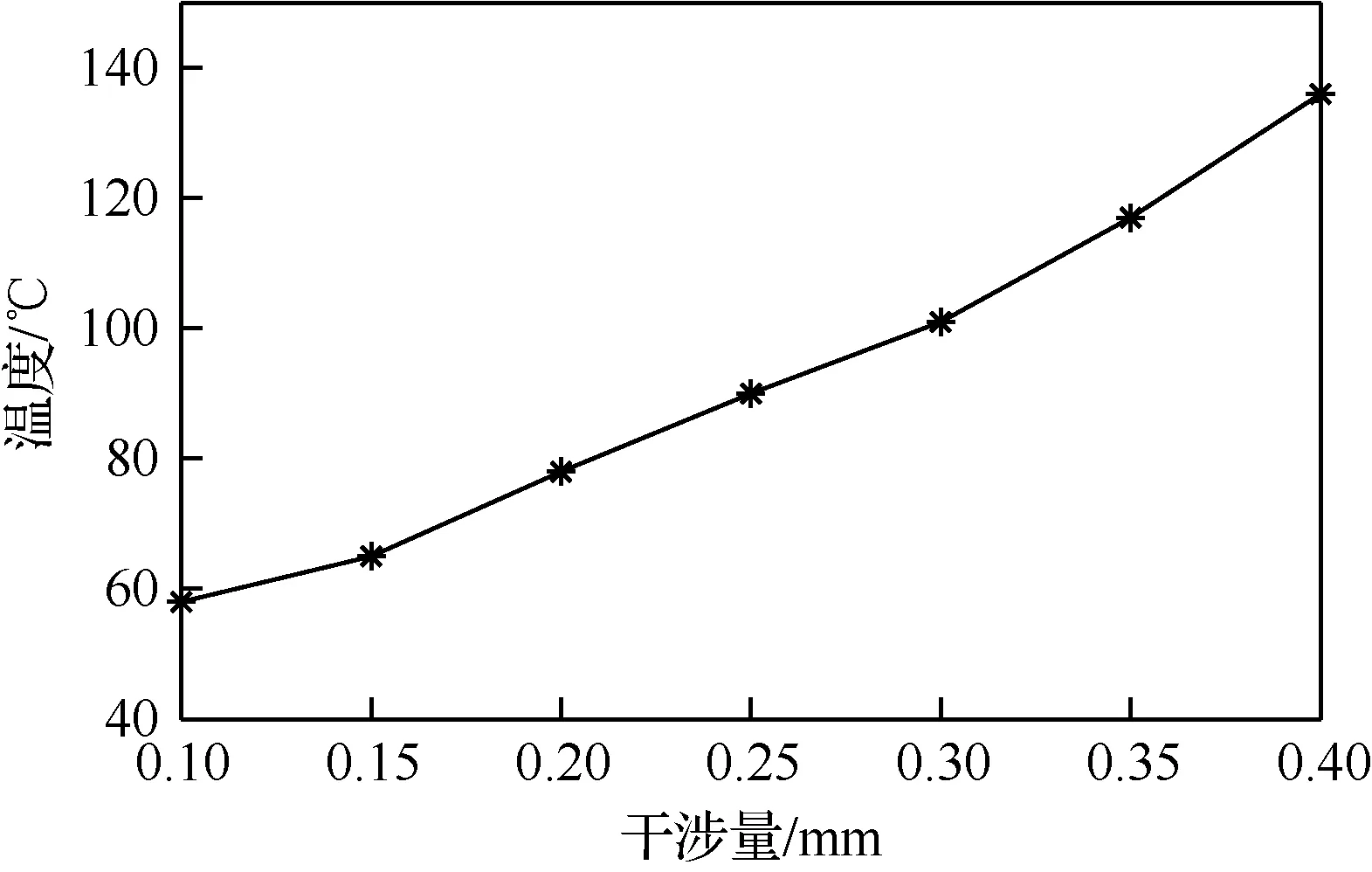
图20 刷式密封最高温度随干涉量变化曲线
4 结 论
1) 建立了基于三维实体的刷式密封刷丝-转子系统热固耦合数值模型,最高温度数值计算值与实验测量值的平均误差为8.9%,刷丝-转子系统热固耦合模型具有较高准确性。
2) 刷式密封最高温度随刷丝束厚度增大逐渐增大;刷丝束最高温度随着后挡板长度减小而逐渐降低;最高温度随干涉量的增大逐渐增大,0.4 mm相较于0.3 mm干涉量最高温度升高了59.0 ℃,随着摩擦时长增大,刷丝与转子磨损量减小,温度呈线性逐渐下降。
3) 刷丝束应力最大值出现在刷丝固定端,接触变形最大值出现在中排刷丝尖端,最大温度值出现在刷丝自由端。刷式密封最高温度随着刷丝安装角的增大而降低;最高温度随着转速的上升逐渐增大,2000 r/min转速相对于600 r/min转速最高温度提高了4.3倍;最高温度随干涉量的增大而逐渐增大,0.4 mm干涉量相对于0.3 mm干涉量最高温度提高了1.34倍。

