基于映射函数的新型五阶WENO格式

刘博，李诗尧，陈嘉禹，程启豪，时晓天,*

1.中国航天空气动力技术研究院，北京 100074

2.中国科学院 力学研究所 高温气体动力学国家重点实验室，北京 100190

3.中国科学院大学 工程科学学院，北京 100049

4.天津大学 水利工程仿真与安全国家重点实验室，天津 300072

5.天津大学 建筑工程学院，天津 300350

6.天津大学 数学学院，天津 300350

随着航空航天技术的发展，计算流体力学(CFD)逐渐成为研究各类复杂气体流动问题的主要手段，而计算机科技的进步为数值模拟提供了更广阔的前景。针对有强非线性效应的物理问题(诸如激波问题)，使用拥有良好频谱性的线性格式计算会出现非物理振荡，严重时甚至会使计算发散，即使加密网格也不会减弱振荡[1]，为解决此类问题需要发展非线性格式。TVD(Total Variation Diminishing)格式[2]具有良好的分辨率和稳定性,但是精度较低。DG(Discontinous Galerkin)[3]、FR(Flux Reconstruction)[4]等有限元方法虽然可以适应非结构网格，但在捕捉间断方面仍有待完善。Harten[5]和Shu[6]等把TVD格式要求降低为满足总变差有界TVB(Total Variation Bounded)的条件，提出了ENO(Essentially Non-Oscillatory scheme)格式。在此基础上，Liu等[7]首次提出WENO(Weighted Essentially Non-Oscillatory scheme)思想，Jiang和Shu[8]随后提出光滑因子和加权系数具体的表达式，并提出了三阶和五阶的WENO格式，此格式适合处理含有间断的问题，被广泛使用[9-14]。然而WENO-JS格式在极值点处的精度会降低，Henrick等[15]分析了其原因并通过引入映射函数重构加权系数，提出了WENO-M格式，Borges[16]和Castro[17]等对光滑因子进行改进，形成WENO-Z格式，克服了极值点降阶的缺陷。随后有研究者提出一系列针对WENO-Z的改进方案[18-20]，但仍然改进不了耗散较大的缺陷。Wu等[21]通过数学推导指出WENO-Z格式在高阶极值点处会降阶。为了减少耗散，Fan[22]提出WENO-η格式，Ha等[23]提出WENO-NS格式。另有研究人员基于Henrick的思想，构造新的映射函数，例如Feng等[24]将WENO-M格式推广到更高阶情形，提出WENO-IM格式，随后Feng等[25]又提出在端点处应接近ENO性质，改进得到WENO-PM格式。Li[26]和刘朋欣[27]等则认为在端点处应逼近恒等映射，提出WENO-PPM格式。Wang等[28]通过大量实验发现映射函数在右端点处的导数影响微小，从而改进出振荡更小的WENO-RM格式。Vevek等[29]提出基于变化因子λ的WENO-AIM格式。

基于映射函数思想重构加权因子，大多数已有的映射函数都是多项式型函数，为了提高函数在端点处的收敛速度与理想权重值处稳定性，以指数函数作为基函数构造分段映射函数WENO-Pe(Piecewise exponential mapping function)，使其匹配常用WENO格式，并以五阶为例通过若干经典算例验证，与其他格式对比来验证新格式的性能。

1 问题描述与数值离散

1.1 标量方程

一维对流方程是最简单的双曲线偏微分方程，该方程可分为线性与非线性两类：

(1)

(2)

1.2 矢量方程

无黏性流体动力学中最重要的基本方程，即Euler方程组，是指对无黏性流体微团应用牛顿第二定律得到的运动微分方程。以一维守恒的情形为例:

(3)

式中：

(4)

其中：ρ、u和p分别代表流体密度、速度与压强；E为单位体积流体的总能量，其表达式为

(5)

式中：γ为气体常数。

1.3 数值离散

在对Euler方程组离散时，采取Steger-Warming流通矢量分裂法，通量F分解为正负两部分分别参与运算：

F=F++F-

(6)

(7)

再对时间导数项进行离散，为了与空间项精度匹配，所用的五阶格式均采用三阶精度的Runge-Kutta格式[30]：

(8)

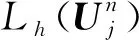
2 通量重构

2.1 WENO格式思想

(9)

该函数是通过每个子模板上使用Lagrange插值多项式得到代数多项式，正负通量模板如图1(a)和图1(b)所示。

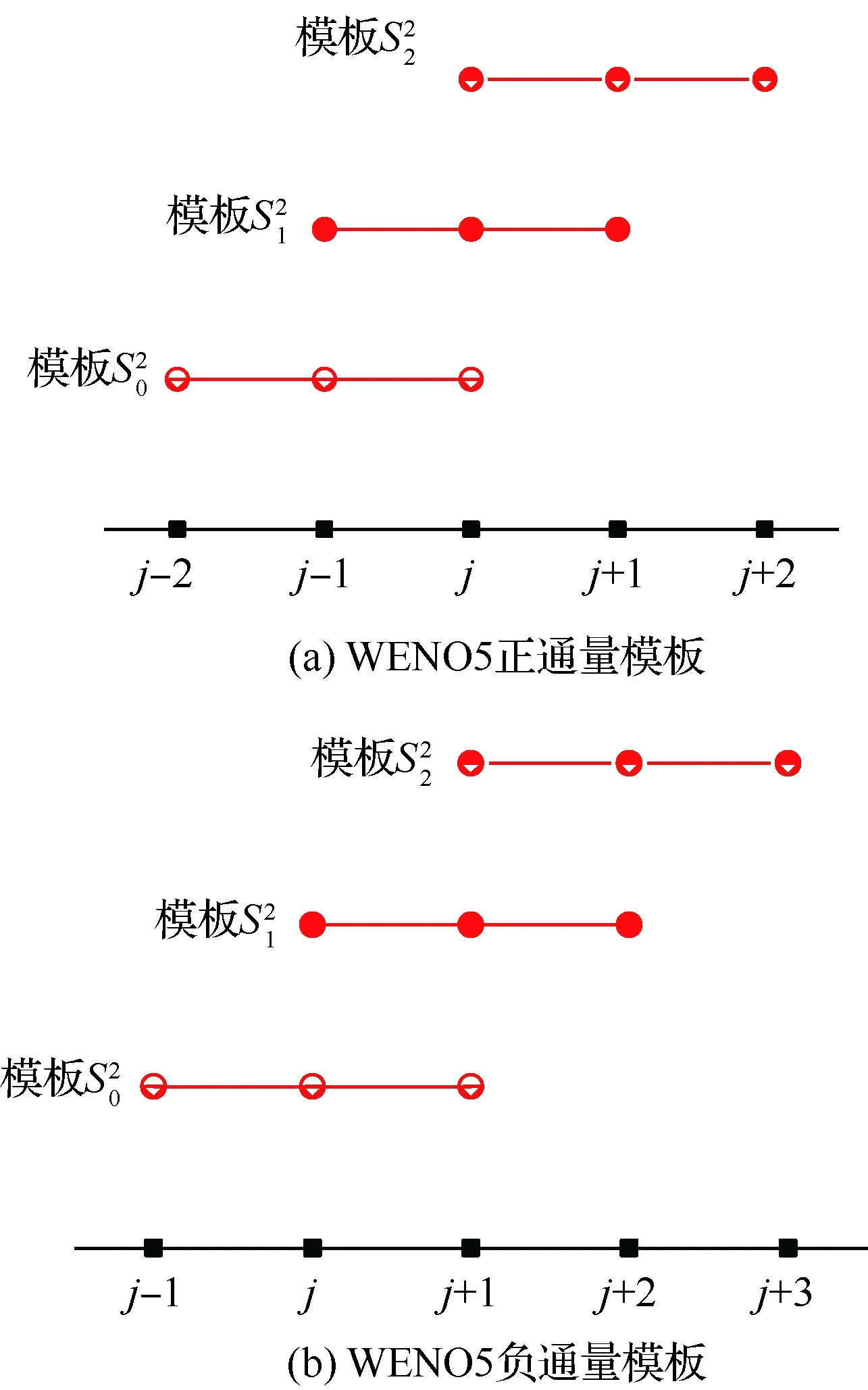
图1 WENO5总模板与子模板

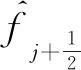
(10)

(11)

并要求非线性权在光滑区域充分接近理想权重，在间断附近退化为ENO格式，以保证减小振荡，因此构造合适的非线性权成为关键问题。

2.2 各类非线性权

2.2.1 WENO-JS格式

(12)

并提出一种非线性权构造方案：

(13)

式中:p为≥2的正整数;ε为防止分母为0的充分小正数，通常取10-6。

2.2.2 WENO-M格式

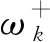
(14)

再将新得到的函数值重构为权重系数：

(15)

注意到该映射函数在(0,1)区间内严格单调递增且具有二阶连续导数，同时还应当满足如下性质：

(16)

通过将ωM,k表达式在Ck点做Taylor展开可以证明：

ωM,k=Ck+O(Δx3)

(17)

2.2.3 WENO-PPM格式

Li等[26]认为映射函数应经过映射以后的非线性权在定义域边界处应尽快地收敛到0或者1，于是提出分段多项式函数作为映射函数：

(18)

其重构加权因子为

(19)

2.2.4 WENO-PM格式

Feng等[25]注意到，Henrick等提出的映射函数(14)在端点处导数值偏大:

(20)

这样会使靠近端点处的权重被放大，出现较大误差，为了修正此问题，Feng等在式(16)基础上对映射函数补充了新要求，即端点处函数的趋近速度：

g′(0)=g′(1)=0

(21)

并设计出新的映射函数：

gPM(ω)=

(22)

使用五阶WENO格式时推荐参数n=4，重构权重系数为

(23)

2.2.5 WENO-RM格式

Wang等[28]认为分段函数的全局光滑性不足，应使用全局高阶连续函数克服来自不光滑模板的影响，故提出新的映射函数：

(24)

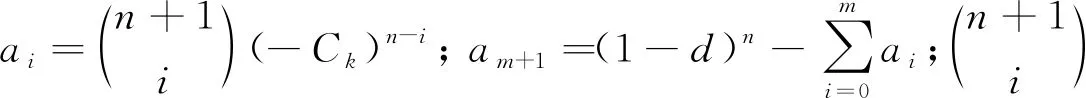
(25)

函数(24)仍然具备如下性质：

(26)

2.2.6 WENO-Pe格式

总结以上的研究，一个好的映射函数应具有如下特点：

1) 在(0,1)区间内具有良好的光滑性。

2) 在各阶极值点处精度不下降。

3) 有较强的克服不光滑模板的能力。

4) 在g(0)处平缓收敛到0。

5) 在g(1)处接近恒等映射。

多项式函数在固定区间的增长速率依赖次数与系数，故考虑使用其他类型函数替代，而指数函数具有无穷次可导且增长率较大的良好性质，可考虑使用其构造映射函数，使该函数具有如下性质：

(27)

2.3 构造WENO-Pe格式的非线性权

以Ck为分界点，将[0,1]区间分为[0,Ck)和[Ck,1]，在左半端内设

(28)

(29)

在右半段内设

(30)

αR,mR+1tRn+mR+1)+Ck

(31)

式中：AL和AR为正实数；mL、mR、n是正整数(n≥m≥2)；αL,i和αR,i是由AL、AR、mL、mR和n确定的系数，对于五阶WENO而言，取n=5，mL=mR=2(一般情况下取mL=mR，以下简称m)，并且AL=AR即可。易证

(32)

为使在左端点处表现为ENO性质，需满足

(33)

则αL,i应满足：

(34)

同样，为使右端点满足WENO性质，需满足：

(35)

αR,i应满足

(36)

式中：

(37)

因此整体有

(38)

(39)

图2是AL=AR=15时，五阶WENO-Pe格式关于3个理想权重的映射函数图像。

图2 WENO5-Pe的映射函数

图3是映射函数gPe同其他映射函数(按其文献中推荐的最佳参数)图像对比，其中各函数的具体参数如下：

(40)

图3 WENO5格式中第2个模板的Pe格式的映射函数与M、IM、PPM、RM和PM函数的对比

如果应用于(2r-1)阶WENO格式，可取n=r+2,m=r-1，相应的系数为

P(n+m;n,i,m-i)

(41)

式中：i=0,1,…,m；αR,0和αR,mR+1表达式同式(36)；P(n;q1,q2,…,qk)为多重全排列：

(42)

3 格式性能分析

3.1 截断误差

(43)

将光滑函数IS在xj处做Taylor展开

(44)

Henrick等[16]指出在f的一阶极值点x0处，即x→x0时有

f′(x)～O(Δx)

(45)

(46)

根据映射函数重构的权重系数，在ω=Ck处进行Taylor展开有

(47)

即有

(48)

只要n取不小于2的正整数, 该格式就能在极值点处达到空间上的五阶精度。

3.2 频谱性

WENO是非线性格式，其频谱性分析与线性格式Fourier频谱分析类似，可以使用Pirozzol提出的近似法色散关系(ADR)。令fj=eikxj，其中i为虚数单位，则

fj+n=eikxj+n=fjeikxn

(49)

由此可以推出修正波数：

K=Re(k)+iIm(k)

(50)

具体可参照文献[32-33]。其中,实部Re(k)代表色散误差，虚部Im(k)代表耗散误差。图4是格式WENO-Pe与其他格式的频谱性对比，系数同式(34)和式(35)，其中WENO-AIM系数选择k=4，m=2，C=104。

从图4可见，WENO-Pe格式的色散误差与数值耗散性均小于其他格式。

4 数值实验

无特殊说明，本文的算例均采用无量纲形式的方程。

4.1 精度验证

4.1.1 定常问题

下面验证WENO5-Pe格式捕捉高阶极值点的性能，仿照文献[34]，构造如下函数族：

u0(x)=ea(x+1)xn+1

(51)

式中：a= 0.5；n为非负整数，当n=0时，该函数在[-1,1]上无极值点；当n= 1时，在此区间上只有唯一的一阶极值点0；当n> 1时，仅有唯一的一阶、二阶极值点0。设N为网格数，分别使用WENO5-Pe、WENO5-PPM、WENO5-RM和WENO5-IM格式，具体格式参数同式(40)，在不同网格下计算其一阶导数，选取n= 0、1、2时的函数，统计数值解在x= 0处与真实值的误差并计算误差阶，结果如表1所示，关于WENO5-Z在极值点处降阶可参考文献[21]。由表1可见，WENO5-PPM格式在无极值点或仅有一阶极值点情况下能达到五阶，但有二阶极值点时，明显下降到三阶左右；WENO5-RM和WENO5-IM在一阶极值点处就会降阶到三阶，有二阶极值点时甚至降到更低的二阶；而WENO5-Pe格式无论有无二阶极值点均能保持在五阶左右精度，且在相同网格下，WENO5-Pe格式的误差更小，这表明提出的格式具备更高的精度。

表1 4种数值格式计算结果对比(定常问题)

4.1.2 非定常问题

本节验证一维线性对流方程，该算例选自文献[15]：

(52)

此问题存在精确解：

(53)

显然，这是一个周期为2的函数，且存在2个一阶极值点和一个二阶极值点，无三阶极值点。选取时间步长为Δt=h5/3(匹配精度)。分别使用WENO5-Pe、WENO5-PPM、WENO5-RM、WENO5-IM和WENO5-Z格式计算到时间t=2.2和t=3(均无量纲，下文同)，统计L2误差及精度阶，如表2所示。

(54)

由表2可以看出，WENO5-Pe、WENO5-PPM、WENO5-RM、WENO5-IM和WENO5-Z格式均能达到预期精度，但WENO5-Pe的精度要优于其他4种格式。

4.2 耗散验证

为了验证WENO5-Pe格式长时间计算的稳定性，选取如下一维对流方程：

(55)

式中:取C=10 000，a=-0.5;分别使用WENO5-Z、WENO5-PPM、WENO5-RM、WENO5-IM和WENO5-Pe格式计算到时间t=100，计算域为[-1,1]，选取网格N=100、N=200、CFL=0.5，得到计算结果如图5所示。

由图5可见，使用同阶格式时，WENO5-PPM与WENO5-RM效果相似，其耗散均小于WENO5-IM，WENO5-IM在网格加密后会出现较大非物理振荡，而WENO5-Pe更接近于真实值，比其他4个格式的耗散更小，能够更精确地捕捉高阶极值点。

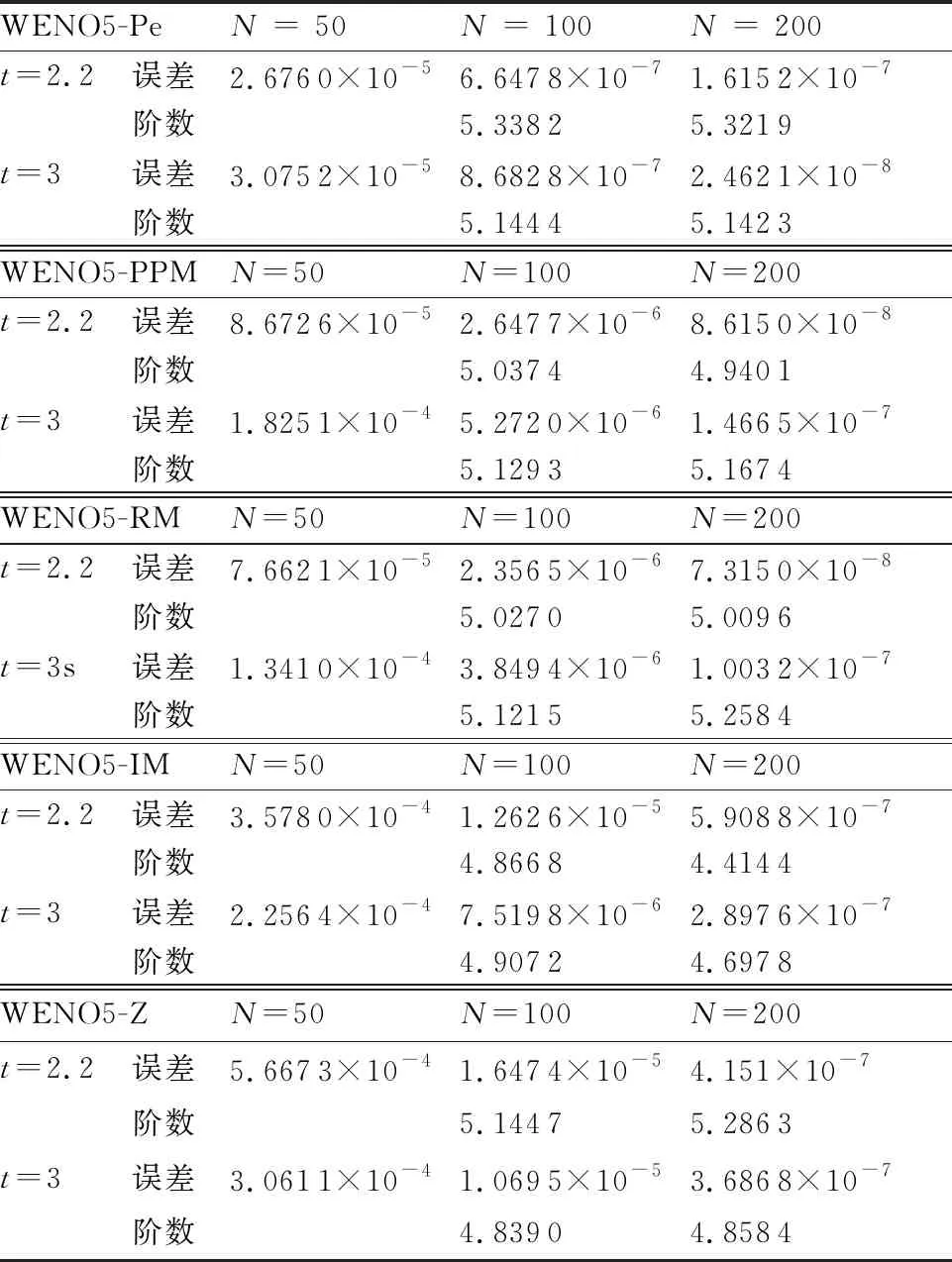
表2 5种数值格式计算的结果对比(非定常问题)

图5 WENO5-Z、WENO5-PPM、WENO5-RM、WENO5-IM和WENO5-Pe格式长时间计算的稳定性

4.3 Sod激波管

该算例的初始条件为[35]

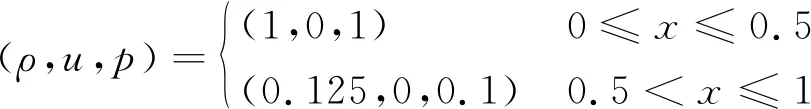
(56)

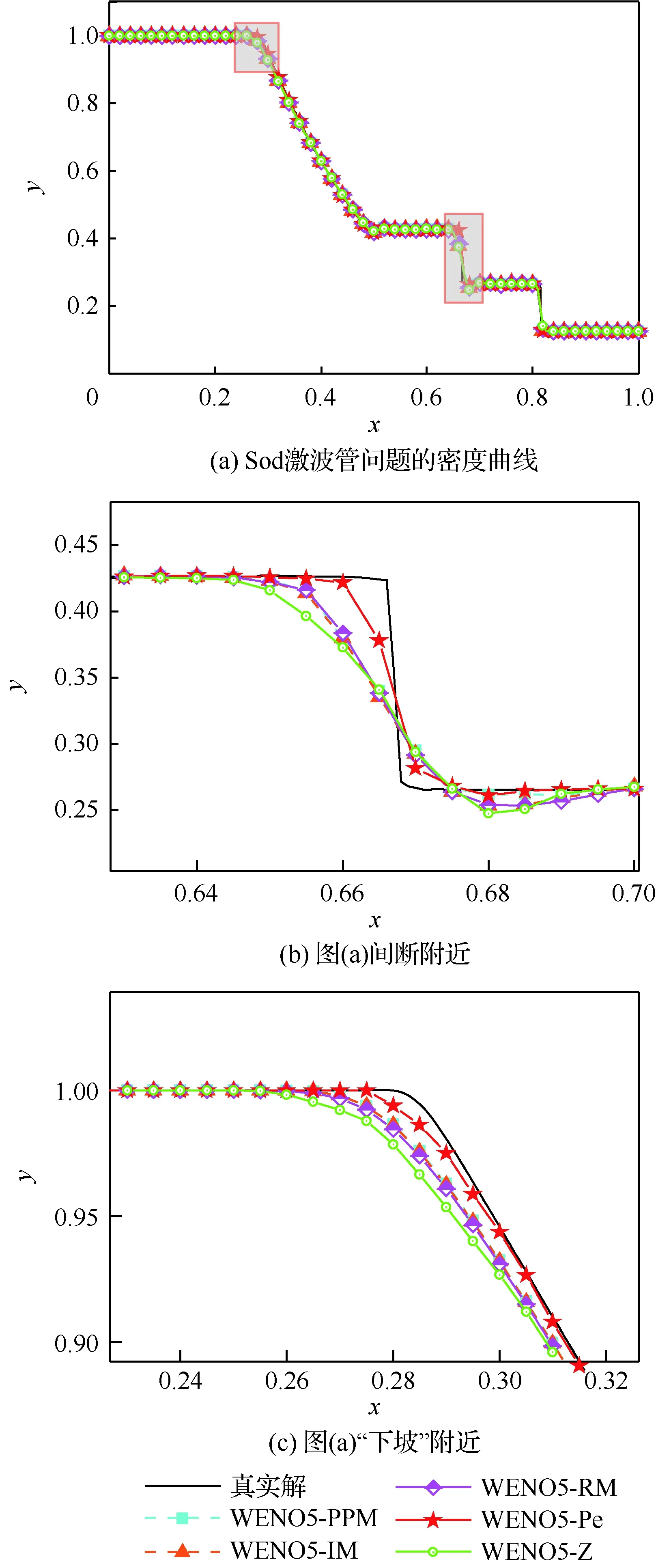
图6 WENO5-Z、WENO5-PPM、WENO5-RM、WENO5-IM和WENO5-Pe格式模拟Sod激波管

设置两边界为流边界，网格数J=200，计算时间为t=0.18，CFL=0.4, 并将WENO5-JS在2 000个网格下的计算结果作为准精确解，分别使用WENO5-Z、WENO5-PPM、WENO5-IM、WENO5-RM和WENO5-Pe格式，得到密度曲线如图6所示。由文献[16,24,26,28]的数值实验可知，WENO5-Z、WENO5-PPM、WENO5-IM和WENO5-RM均比WENO5-Z计算效果好，而从图6可见，WENO5-Pe的捕捉间断能力相较于以上格式有明显提升。

4.4 Lax激波管

此算例[36]描述的流场中同时包含有激波、接触间断、膨胀波和平滑区域，其初始条件为

(ρ,u,p)=

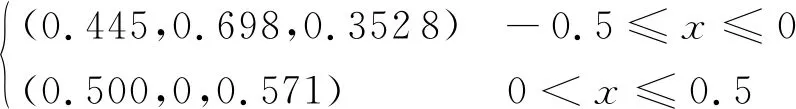
(57)

网格数J=200、CFL=0.2，计算终止到t=0.16，并将WENO5-JS在2 000个网格下的计算结果作为准精确解，分别使用WENO-Z、WENO5-PPM、WENO5-IM、 WENO5-RM和WENO5-Pe格式，得到密度曲线如图7所示。由图7(a)～图7(c)可见，WENO5-Pe更接近于真实解，产生的非物理振荡更小，在间断处的识别更加敏感，鲁棒性更强。

图7 WENO5-Z、WENO5-PPM、WENO5-RM、WENO5-IM和WENO5-Pe格式模拟Lax激波管

4.5 Osher-Shu问题

该问题[37]描述一道马赫数3 的右行激波与熵波的相互作用，熵波在激波作用下被压缩，并向下游传播方向生成一系列声波。此算例可以检验数值格式的间断识别能力、稳定性和分辨率，其初始条件为

(58)

选取网格点J= 240、CFL = 0.4，计算终止时间为t= 1.8，分别使用WENO5-Z、WENO5-PPM、WENO5-IM、WENO5-RM和WENO5-Pe格式计算该问题, 选取WENO5-JS格式在2 000个网格下计算结果为准精确解，得到密度曲线如图8所示，统计计算所用时间如表3所示。

由图8可见，在同样网格下WENO5-Pe格式具备更好的分辨率，而且比其他4个格式计算出的函数极值点偏移量明显的小，而WENO5-Z的分辨率要略差于其他4种基于函数映射的WENO格式，说明WENO5-Pe的色散误差更小。

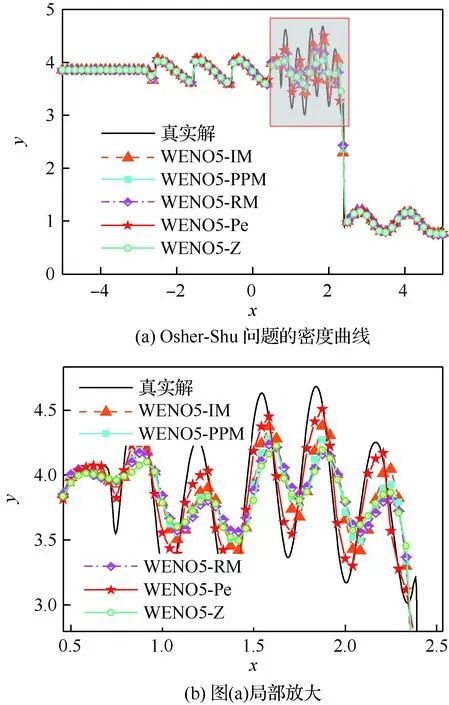
图8 WENO5-Z、WENO5-PPM、WENO5-RM、WENO5-IM和WENO5-Pe格式模拟Shu-Osher问题

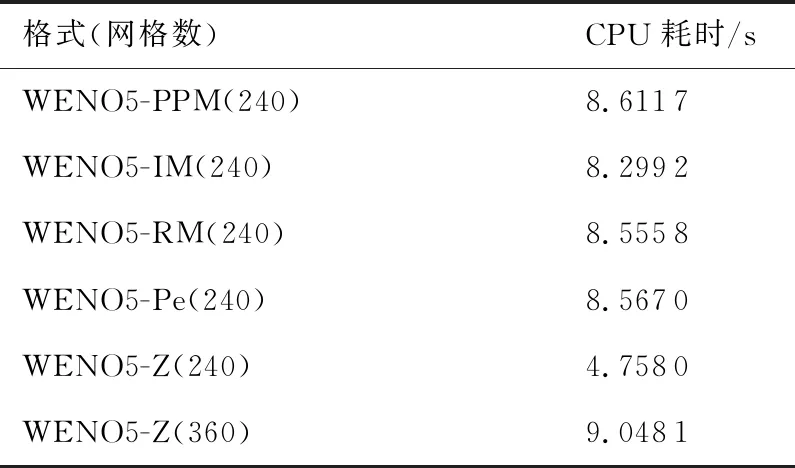
表3 指定网格下各格式计算耗时

另一方面，使用网格N= 360的WENO5-Z格式，与N= 240的WENO5-Pe格式计算结果对比，可见在CPU耗时接近的情况下，240网格数的WENO5-Pe计算效果依旧优于360网格数的WENO5-Z计算效果。

从以上一维的算例中不难看出，WENO5-IM与WENO5-PPM在精度与分辨率的表现上都优于WENO5--RM和WENO5-Z，而WENO5-Pe对极值点捕捉位置、识别间断的敏感性、数值精度以及计算的鲁棒性都要优于其他4个格式。

4.6 二维格式性能验证

二维欧拉方程的控制方程为

(59)

式中：

(60)

通量F与G的离散与分裂形式与一维情形一致。下面分别选取对流问题与定常问题分别验证格式精度与收敛性。

4.6.1 精度验证

二维对流问题：

(61)

该问题存在精确解：

u(x,y,t)=sin(x+y-2t)+1.200

(62)

且不需要通量分裂，可以更好地检验格式精度，分别使用WENO5-Z、WENO5-PPM、WENO5-IM、WENO5-RM和WENO5-Pe在不同网格下计算到t= 0.2和t= 1.2时刻，统计L2误差并计算误差阶，结果如表4所示。通过表4可见，5种格式在达到理论精度阶的同时，WENO5-Pe的精度要略优于WENO5-PPM、WENO5-IM和WENO5-RM，而它们均优于WENO5-Z。

4.6.2 平板激波反射问题

有一道与x方向成29°角的激波射向平面上一壁面，并与壁面碰撞进而发生反射，形成入射波和反射波[38]，如图9(a)所示。当流动达到稳定后，该问题存在精确解，如图9(b)所示，该问题属于无黏流动，可以用Euler方程描述该过程。该问题的计算域为[0,4]×[0,1]的矩形区域，当t= 0时，使激波刚好与底部壁面相遇，具体初始条件可以根据激波前后密度、压强等相关公式计算，其左侧初始条件：

(63)

顶部初始条件：

[1.699 97,2.619 34,-0.506 32,1.528 19]

(64)

表4 5种数值格式在二维算例下精度对比

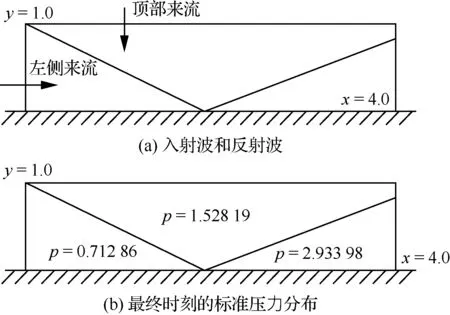
图9 二维平板激波反射示意图

式中：右侧边界为自由流出条件，底部边界为反射条件。分别使用WENO5-Z、WENO5-PPM、WENO5-IM、WENO5-RM和WENO5-Pe在200×50的网格下计算该流动，终止时间为t=4.5，CFL=0.5。将计算获得的结果与精确解对比，结果如图10所示，并统计L2误差如表5所示。

另外，比较相同网格下不同格式的L2误差随迭代步数发展的关系曲线如图10(e)和图10(f)所示，从而对比其收敛速度，计算网格仍然为200×50。在相同网格，相同物理时间下，从图10(a)～图10(c)可见，WENO5-Pe的分辨率更高，稳定性更好，捕捉激波的位置更准确，非物理振荡更小，而WENO5-Z对激波初始位置的捕捉误差较大，WENO5-IM出现了较明显的非物理振荡；通过表5可见，计算到相同时刻WENO5-Pe的精度高于其他五阶格式；通过图10(e)和图10(f)可见，相同网格和耗时的情况下，WENO5-Pe相较于其他格式计算到收敛的耗时更短，而最终收敛时的精度也更高。

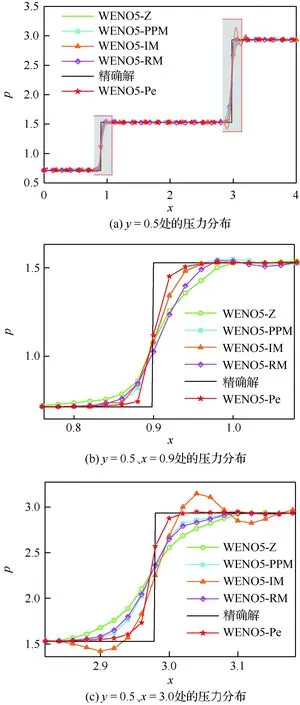
图10 WENO5-Z、WENO5-PPM、WENO5-RM、WENO5-IM和WENO5-Pe格式模拟平板激波反射问题

表5 5种WENO格式计算二维激波反射到t=4.5时刻得到的结果对比

4.7 二维Riemann问题

该问题选自Liu等的数值实验[39]，初始时刻4个计算子区域内流体有不同的初值，当瞬间除去4个计算子区域内膜后，在计算区域形成激波、涡和接触间断相互作用的复杂流动。该问题求解域为[0,2]×[0,2]，初始条件为

(65)

4条边界均为自由输出边界，即在每一条边界上，都有

(66)

使用400×400均匀网格，计算终止时间t=0.8,条件数CFL=0.5,分别使用五阶的WENO5-IM、WENO5-PPM、WENO5-RM、WENO5-Z和WENO5-Pe计算其流场变化。图11(a)～图11(e)是从0.2～1.7的30条密度等值线。

观察图11(a)～图11(e)可见，WENO5-RM和WENO5-PPM比WENO5-Z的分辨率更高，同时WENO5-IM比WENO5-RM和WENO5-PPM的分辨率稍高，而WENO5-Pe比WENO5-IM的分辨率更明显，可以观察到更多的涡结构细节，密度的分界线轮廓也更精准，由此可见其捕捉流场细节能力更强。

4.8 Rayleigh-Taylor不稳定性问题

该算例描述初始流场中存在两种密度不同的流体，在重力场作用下，位于上方的密度较大的流体加速进入下方的密度较小的流体的失稳过程，最终形成复杂的流场[40]。其计算域为[0,0.25]×[0,1]，计算初始条件为在控制方程式(59)和式(60)右侧添加源项以模拟重力影响。

(67)

S=[0,0,ρ,ρv]T

(68)

气体指数取γ=5/3，设置左右边界为反射壁面，上下边界设为常值。

(69)

计算网格为240×960，计算终止时间t= 1.95，CFL = 0.5, 图12(a)～图12(e)给出的是5种WENO格式的计算结果，密度等值线为0.965 0～2.1481之间15等份。

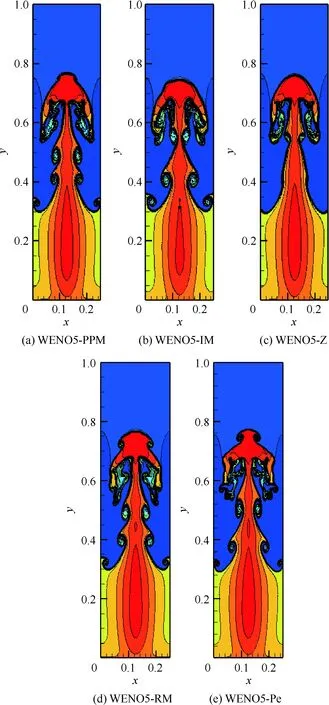
图12 WENO5-Z、WENO5-PPM、WENO5-RM、WENO5-IM和WENO5-Pe格式计算Rayleigh-Taylor问题得到的密度等值线

由图12可见，同样网格下WENO5-Z分辨率最低，甚至在y= 0.5附无法识别涡结构，WENO5-RM的分辨率略高于WENO5-PPM和WENO5-IM，而WENO5-Pe的分辨率更好，能够在扩散界面捕捉到更多流场结构。

4.9 双Mach反射问题

强激波双Mach反射问题[41]是测试数值格式分辨率的经典算例之一。本算例的计算域为[0,4]×[0,1], 初始条件为一道与x轴正方向成60°，Ma= 10的右行斜激波在x= 1/6处与下壁面相遇，激波一直延伸至上壁面，其右侧参数[ρ,u,v,p]为[1.4,0,0,1.0]，左侧参数为[8.0,7.144 7,-4.125,116.5]。上边界条件按激波传播精确解给出，左边界与x≤1/6的下边界按流入条件给出，右边界为流出条件，x>1/6的下边界部分为壁面条件。计算网格为960×240，终止时间为t=0.2，CFL = 0.5，图13(a)～图13(e)为最终时刻尾部区域5种WENO格式计算的密度2～22的40条等值线图。

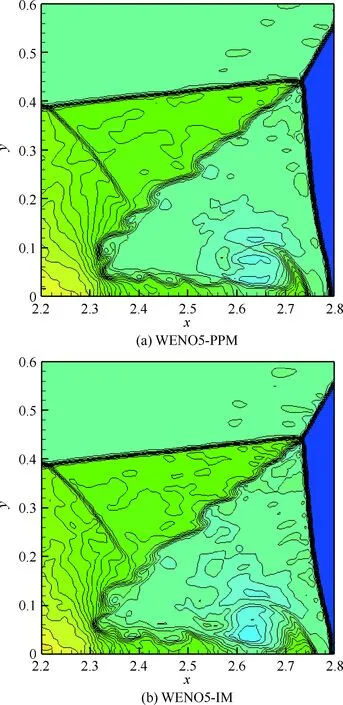
图13 WENO5-PPM、WENO5-IM、WENO5-RM、WENO5-Z和WENO5-Pe格式计算双马赫反射问题得到的密度等值线

由图13可见，WENO5-Z、WENO5-PPM和WENO5-RM格式的计算结果相似，三者的分辨率略低于WENO5-IM，而WENO5-Pe的分辨率又高于WENO5-IM，其计算结果显示的激波更清晰，滑移线上卷起的涡结构也更丰富。

5 结 论

针对传统WENO格式在极值点处精度降低的情况，本文基于对权重系数重构的思想，设计出一族以WENO-JS格式的权重系数为自变量的映射函数，从而得到新格式WENO-Pe，克服了一阶和高阶极值点处降阶的缺陷，且可以推广到高阶格式，并通过数值实验与其他格式对比验证了WENO-Pe格式的性能：

1) WENO-Pe格式的色散误差与数值耗散均小于WENO-JS、WENO-Z、WENO-M以及列举的其他映射函数型格式。

2) 对比WENO-IM和WENO-RM格式，WENO-Pe在一阶极值点处能够保持理论精度。对比WENO-PPM格式，WENO-Pe在二阶极值点处也基本保持精度不下降。

3) 在相同精度情况下，本文WENO-Pe格式拥有更良好的分辨率，在Riemann问题和双马赫反射问题中，明显可见其计算结果能捕捉更多的间断、涡结构等流场细节。