基于不确定性拔销器的机构运动可靠性分析

杨琨，程涛

基于不确定性拔销器的机构运动可靠性分析

杨琨，程涛

（陕西应用物理化学研究所，西安 710061）

实现拔销器可靠性的定量分析和高效精确评估，研究拔销器工作过程中随机变量对可靠性的影响，提出一种基于不确定性的拔销器机构运动可靠性建模与分析方法。首先，基于应力–强度模型和拔销器的机构运动失效模式，建立极限状态方程；然后，综合考虑工作过程中不确定性因素的影响，采用基于Kriging代理模型逼近极限状态方程的机构运动可靠性分析方法，对拔销器的机构运动进行高效可靠性分析；最后，对拔销器机构运动中的随机变量进行可靠性灵敏度分析，确定随机变量对拔销器的机构运动的可靠性影响程度，为优化设计提供方向。拔销器机构运动的可靠度均大于0.999 9，达到设计要求。影响拔销器活塞启动可靠性最大的是剪切销直径，其次是、、等，影响活塞运动可靠性最大的是，其次是、。该方法能够准确描述不确定性因素对拔销器机构运动的影响，提升机构运动可靠性定量分析的精度和效率，为拔销器的精细化设计提供了理论支撑。

拔销器；可靠性分析；Kriging模型；灵敏度；不确定性

拔销器是通过起爆器产生的高温高压气体推动机械机构运动的火工装置，具有体积小、质量轻、作用可靠等特点，能够有效降低总体承载方向的冲击，该类装置已广泛用于航天系统[1-2]。

近年来，针对拔销器的可靠性设计仅是采用冗余或裕度设计来保证产品的可靠度[3-4]，或者通过数值模拟[2]，从单因素的角度出发考虑对产品的影响，以提高产品可靠性。这些方法缺乏对产品设计可靠度的定量认识，随着拔销器在航天航空的应用越来越普遍，对其可靠性的要求越来越高，急需开展对拔销器机构作动可靠性分析，了解外部载荷、材料属性、结构尺寸等因素对拔销器机构作动可靠性的影响规律，以便采取设计措施，提高拔销器机构作动的可靠性水平。拔销器机构作动属于机构运动可靠性范畴[5]，针对机构运动可靠性方法主要分为近似解析法[6-7]、数字模拟法[8]、代理模型法3类[9-10]。其中，代理模型法由于有较高的求解效率，被广泛使用，特别是Kriging代理模型法[11]，与其他代理模型相比，具有插值精度高和预测准确的优点[12-13]。

本文以某拔销器为研究对象，建立了拔销器机构运动动力学仿真模型，通过综合考虑拔销器机构运动不确定性因素的影响，基于应力强度干涉模型，建立了拔销器作动极限状态函数。最后，采用Kriging代理模型和蒙特卡洛方法相结合的方法进行了可靠性分析和灵敏度分析，量化材料参数、结构尺寸、火药参数等不确定性对拔销器工作可靠性的影响。

1 拔销器的结构及工作原理

拔销装置主要包括主装药、起爆器、螺盖、活塞、剪切销、密封圈等部件，如图1所示。在工作前，为了限制活塞运动，拔销器使用剪切销将活塞和壳体定位，实现对航天器机械结构的锁定。在接到起爆信号后，起爆器作用，点燃主装药，产生的高温高压燃气通过壳体传火孔进入组合件密封壳体腔内，推动活塞运动，活塞前进，剪断剪切销，活塞沿轴线方向回缩，运动到位后，完成解锁功能。

2 建立拔销器机构运动极限状态函数

根据拔销器的工作原理，将拔销器的机构运动划分为活塞启动阶段、活塞运动阶段。当其中一个阶段发生失效，最后都将影响拔销器功能的可靠性。因此，将拔销器的机构运动失效模型分为活塞启动失效、活塞运动失效。下面分别建立各阶段运动过程的极限状态函数。

图1 拔销器的结构

2.1 建立拔销器的活塞启动极限状态函数

活塞启动失效指活塞不能克服剪切销的剪切力和密封圈的摩擦力，导致活塞不能启动，该阶段如图2所示。

图2 拔销器的机构启动阶段

因此，根据应力–强度干涉理论[14]和拔销器的机构运动失效模式，活塞启动阶段的极限状态函数1为：

式中：s为剪切销剪切力；f密封圈的摩擦力；p为起爆器输出的压力。

根据文献[15]，密封圈摩擦力f的计算公式为：

式中：m为密封圈与外筒内壁之间的摩擦系数，取值为0.4；m为密封圈材料的弹性模量，取值为7.84 Pa；m为密封圈外径，m；m为圆截面直径，m；为密封圈材料的泊松系数，取值为0.47；为预压缩率；m为沟槽底部至外筒内壁的距离，m。

根据文献[16]，剪切销的剪切力s可按照式（3）进行计算。

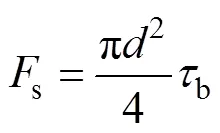
式中：为剪切销直径，取值为0.002 m；b为剪切销材料的剪切强度，MPa。

起爆器输出的压力可以按照式（4）计算。

式中：为输出压力作用在活塞上的面积，m2；为输出压力。

根据文献[17]，对于密闭膛内高温高压燃气，则按照如式（5）计算。

式中：为装药的火药力，J/kg；为装填密度，kg/m3；为余容，m3/kg。

2.2 建立拔销器的活塞运动极限状态函数

活塞运动失效指活塞沿轴线方向回缩时不能克服密封圈的摩擦力，导致活塞未能运动到指定位置，该阶段如图3所示。

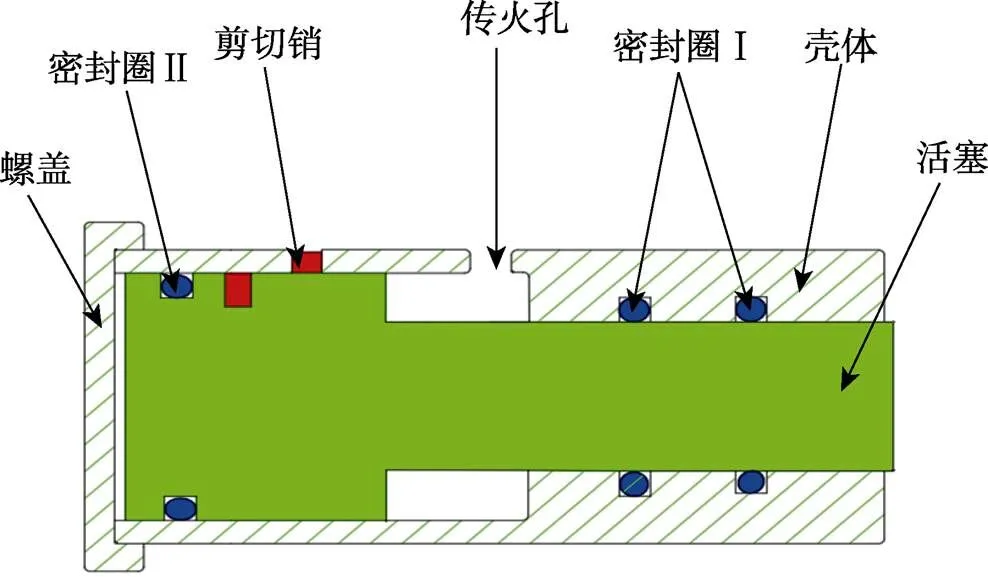
图3 拔销器的机构运动阶段

式中：为活塞运动时间，根据设计要求，为4.45 ms；min为活塞运动的最小距离，根据设计尺寸，min=2.5 mm。

由于拔销器机构运动受到诸多不确定因素的影响，导致极限状态函数涉及到的参数不是定值，所以将极限状态函数中所列出的主要参数作为随机变量来处理。在工程中，零件几何尺寸参数分布一般认为都服从正态分布，设计的名义尺寸作为均值，而标准差是1/6的公差[18]。各参数服从的分布类型和参数值见表1，均采用国际单位。

表1 主要不确定性因素分布类型及其参数

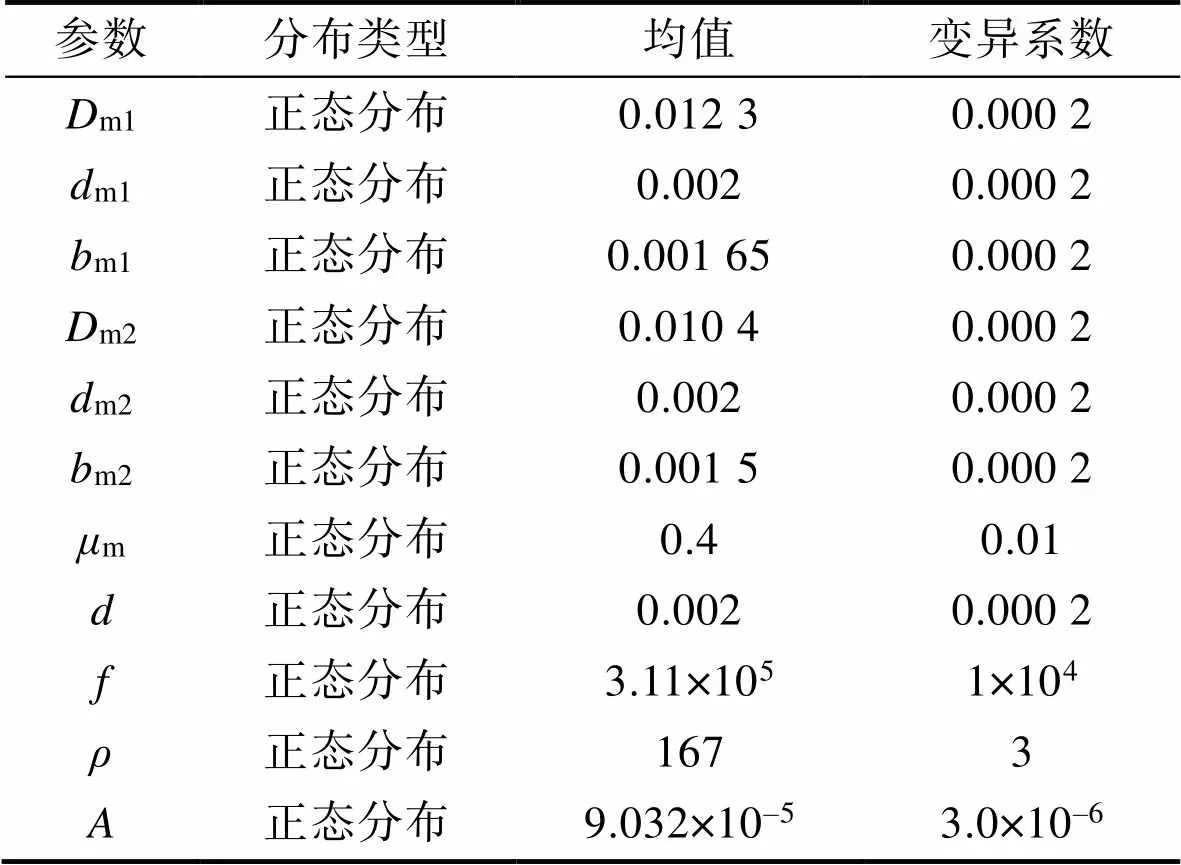
Tab.1 Distribution types and parameters of main uncertainty factors

3 拔销器的机构运动可靠性与灵敏度分析方法

根据可靠性理论，求解拔销器机构运动失效概率的模型为[19]：

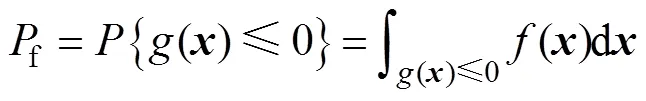
为了求解式（7），将式（7）改写为失效域指示函数I()的数学期望形式[20]，即：

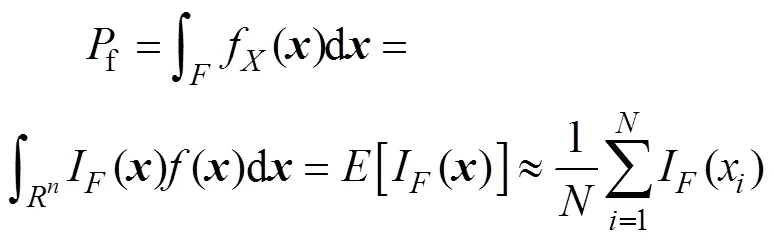
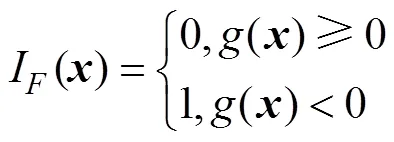
因此，可靠度模型为：

为了提高求解效率，采用Kriging代理模型逼近极限状态函数，进而采用蒙特卡洛法（Monte Carlo Simulation, MCS）求解失效概率的方法。其中，Kriging模型为[21]：

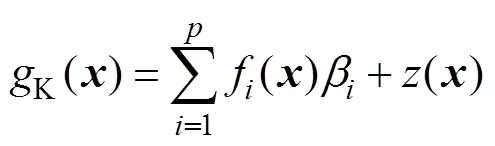
式中：K()为未知的Kriging模型；()为回归基函数，()={1(),2(),…, f()}T；为回归系数，={1,1,…,β}T；表示基函数的个数；()为高斯随机过程。

可靠性灵敏度反映了随机变量对失效概率的影响程度[22]。因此，拔销器机构运动可靠性灵敏度分析的计算公式为[23]：

式中：为随机变量的均值或标准差；=[λ]×n，当=时，λ是第个随机变量的标准差，当≠，其取值为0；为可靠度指标，根据文献[20]，=()；为独立的标准正态随机向量。

4 拔销器的机构运动可靠性结果分析

通过分析拔销器的失效模式，分别建立了拔销器启动阶段和运动阶段的极限状态函数，进而采用拔销器的机构运动可靠性分析方法得到了拔销器机构运动的可靠度，并与传统机构可靠性分析的MCS结果进行对比，结果见表2。

表2 不同方法拔销器的活塞启动和运动阶段可靠性分析结果

Tab.2 Analysis results of the pin puller startup and motion reliability by different methods

根据文献[24]，航天器分离任务所需的结构/机构可靠性为0.999 9。从表2可以看出，拔销器机构运动的可靠性均达到设计要求。通过分析随机变量的灵敏度，得到影响可靠性较大的随机因素，在后续的优化设计进行改进，继续提高拔销器机构运动可靠性。启动阶段和运动阶段随机变量的灵敏度分析如图4所示。

图4 不同阶段随机变量的灵敏度

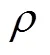
5 结论

本文以某拔销器为研究对象，采用基于Kriging代理模型和蒙特卡洛方法相结合的方法对拔销器机构运动的可靠性进行了分析。选取工作载荷、几何尺寸和火药燃烧参数等随机变量，建立了拔销器机构不同作动阶段的应力强度干涉模型。在拔销器活塞启动过程中，影响可靠性的最主要参数为剪切销直径；拔销器活塞运动过程中，影响可靠性的最主要参数为活塞的受压面积。可通过调节这些设计值的大小提高可靠性，该结果为优化设计提供了方向。

[1] 王凯民, 温玉全. 军用火工品设计技术[M]. 北京: 国防工业出版社, 2006.

WANG Kai-min, WEN Yu-quan. Design of Initiators and Pyrotechnics for Weapon Systems[M]. Beijing: National Defense Industry Press, 2006.

[2] 孙洁, 郭崇星, 吴瑞德, 等. 拔销器作用过程的仿真研究[J]. 火工品, 2017(1): 10-13.

SUN Jie, GUO Chong-xing, WU Rui-de, et al. Simulation Research on the Function Process of the Pin Puller[J]. Initiators & Pyrotechnics, 2017(1): 10-13.

[3] 王鹏, 杜志明. 火工烟火装置裕度研究与设计方法综述[J]. 火工品, 2005(2): 34-38.

WANG Peng, DU Zhi-ming. Summarize of Margin Research and Design Method of Pyrotechnic Devices[J]. Initiators & Pyrotechnics, 2005(2): 34-38.

[4] 荣吉利, 张涛, 董沛武, 等. 冗余设计火工装置的可靠性评定试验方法研究[J]. 北京理工大学学报, 2011, 31(5): 509-513.

RONG Ji-li, ZHANG Tao, DONG Pei-wu, et al. Study on Hardened Test Approach to Reliability Assessment for Pyrote­chnic Devices with Redundancy Design[J]. Transactions of Beijing Institute of Technology, 2011, 31(5): 509-513.

[5] 熊芬芬, 杨树兴, 刘宇. 工程概率不确定性分析方法[M]. 北京: 科学出版社, 2015.

XIONG Fen-fen, YANG Shu-xing, LIU Yu. Engineering Probability Uncertainty Analysis Method[M]. Beijing: Science Press, 2015.

[6] HAOFER A, LIND N. An Exact and Invariant First- Order Reliability Format[J]. Eng Mech ASCE, 1974, 100: 111-121.

[7] LEE I, NOH Y, YOO D. A Novel Second-Order Reliability Method (SORM) Using Noncentral or Generalized Chi-Squared Distributions[J]. Journal of Mechanical Design, 2012, 134(10): 100912.

[8] ZHU Zhi-fu, DU Xiao-ping. Reliability Analysis with Monte Carlo Simulation and Dependent Kriging Predictions[J]. Journal of Mechanical Design, 2016, 138(12): 121403.

[9] BEZERRA M A, SANTELLI R E, OLIVEIRA E P, et al. Response Surface Methodology (RSM) as a Tool for Optimization in Analytical Chemistry[J]. Talanta, 2008, 76(5): 965-977.

[10] ECHARD B, GAYTON N, LEMAIRE M. AK-MCS: An Active Learning Reliability Method Combining Kriging and Monte Carlo Simulation[J]. Structural Safety, 2011, 33(2): 145-154.

[11] KAYMAZ I. Application of Kriging Method to Structural Reliability Problems[J]. Structural Safety, 2005, 27(2): 133-151.

[12] HUANG Xiao-xu, CHEN Jian-qiao, ZHU Hong-ping. Assessing Small Failure Probabilities by AK-SS: An Active Learning Method Combining Kriging and Subset Simulation[J]. Structural Safety, 2016, 59: 86-95.

[13] ECHARD B, GAYTON N, LEMAIRE M, et al. A Combined Importance Sampling and Kriging Reliability Method for Small Failure Probabilities with Time-Demanding Numerical Models[J]. Reliability Engineering & System Safety, 2013, 111: 232-240.

[14] KOTZ S, LUMELSKII Y, PENSKY M. The Stress-Stren­gth Model and its Generalizations - Theory and Applications[M]. HongKong: World Scientific Publishing Co Pte Ltd, 2003.

[15] XU Fu-ren. Calculating Frictional Force Caused by O-Ring Seal[J]. Lubric Ation Engineering,1989(1):32-34．

[16] JIN Zhong-mou. Mechanics of Materials[M]. Beijing: Machinery Industry Press, 2009: 64-65．

[17] JIN Zhi-ming. The Ballistics of Interior Guns[M]. Beijing: Beijing Institute of Technology, 2004: 188-189．

[18] 杨帆. 电连接器锁紧分离机构可靠性设计方法的研究[D]. 杭州: 浙江理工大学, 2017.

YANG Fan. Reliability Design Method of the Locking Mechanism for Electrical Connectors[D]. Hangzhou: Zhejiang Sci-Tech University, 2017.

[19] DITLEVSEN O, MADSEN H O. Structural Reliability Methods[M]. West Sussex: John Wiley & Sons Ltd, 2007.

[20] 吕震宙, 宋述芳, 李璐祎. 结构/机构可靠性设计基础[M]. 西安: 西北工业大学出版社, 2019.

LYU Zhen-zhou, SONG Shu-fang, LI Lu-yi. Foundations of Structural/Mechanism Reliability Design [M]. Xi'an: Northwestern Polytechnical University Press, 2019.

[21] LOPHAVEN S, NIELSEN H, SØNDERGAARD J. DACE a Matlab Kriging Toolbox[K].Copenhagen: Technical University of Denmark, 2002.

[22] IONESCU-BUJOR M, CACUCI D G. A Comparative Review of Sensitivity and Uncertainty Analysis of Large-Scale Systems—I: Deterministic Methods[J]. Nuclear Science and Engineering, 2004, 147(3): 189-203.

[23] SALTELLI A, ANNONI P. How to Avoid a Perfunctory Sensitivity Analysis[J]. Environmental Modelling & Software, 2010, 25(12): 1508-1517.

[24] GONG Qi, ZHANG Jian-guo, TAN Chun-lin, et al. Neural Networks Combined with Importance Sampling Techniques for Reliability Evaluation of Explosive Initiating Device[J]. Chinese Journal of Aeronautics, 2012, 25(2): 208-215.

Motion Reliability Analysis of Pin Puller Mechanism Based on Uncertainty

YANG Kun, CHENG Tao

(Shaanxi Applied Physical-Chemistry Institute, Xi'an 710061, China)

The work aims to study the effects of random variables on the reliability in the working process of pin puller and propose a modeling and analysis method for the motion reliability of the pin puller mechanism based on uncertainty, so as to realize the quantitative analysis and efficient and accurate evaluation of the pin puller reliability. Firstly, based on the stress-strength model and mechanism motion failure mode of the pin puller, the limit state equation was established. Then, considering the effects of uncertainty factors in the working process, a reliability analysis method of mechanism motion based on Kriging surrogate model to approximate the limit state equation was proposed, and the efficient reliability analysis of the mechanism motion of the pin puller was carried out. Finally, the reliability sensitivity analysis was conducted to the random variables in the mechanism motion of the pin puller to determine the effects of the random variables on the motion reliability of the pin puller mechanism, which provided the direction for the optimization design. The motion reliability of pin puller mechanism was more than 0.999 9, meeting the design requirements. The diameter of shear pinwas the biggest factor affecting the startup reliability of pin puller piston, followed by,,,etc. The biggest factor affecting the reliability of piston motion was, followed by,. This method can accurately describe the effects of uncertainty factors on the motion of the pin puller mechanism, improve the accuracy and efficiency of the quantitative analysis of mechanism motion reliability, and provide support for the fine design of the pin puller.

pin puller; reliability analysis; Kriging model; sensitivity; uncertainty

TJ 450

A

1672-9242(2022)12-0014-05

10.7643/ issn.1672-9242.2022.12.003

2022–11–22；

2022–12–10

2022-11-22；

2022-12-10

杨琨（1984—），男，高级工程师，主要研究方向为火工装置设计技术研究。

YANG Kun (1984-), Male, Senior engineer, Research focus: Design technology of pyrotechnic device.

程涛（1971—），男，研究员，主要研究方向为火工系统技术研究。

CHENG Tao (1971-), Male, Researcher, Research focus: pyrotechnic system technology.

杨琨, 程涛. 基于不确定性拔销器的机构运动可靠性分析[J]. 装备环境工程, 2022, 19(12): 014-018.

YANG Kun, CHENG Tao. Motion Reliability Analysis of Pin Puller Mechanism Based on Uncertainty[J]. Equipment Environmental Engineering, 2022, 19(12): 014-018.

责任编辑：刘世忠