大规模考试中数学问题提出能力考查的必要性和可行性研究

陈 玉 婷 章 飞

(1.南京师范大学附属中学仙林学校初中部， 江苏南京 210046； 2.江苏第二师范学院课程与教学研究所， 江苏南京 211200)

近年来，学生的数学问题提出能力成为数学教育领域研究的热点。《义务教育数学课程标准(2022版)》[1]和《普通高中数学课程标准(2017年版)》[2]中都提出，要发展学生发现和提出问题的能力。数学问题提出能力无论对社会发展还是对个人发展都具有重要的价值。基于数学问题提出能力的重要性，应将数学问题提出落实到数学教学、学习及考试当中。而目前极少有关于数学问题提出在考试中的研究，并且尚未形成较为客观统一的数学问题提出评价框架，因此本文以中考等大规模考试中进行数学问题提出能力考查的必要性与可行性为研究切入，建议在中考等大规模考试中增加数学问题提出能力的考查内容，以期切实提升学生的数学素养。

一、问题提出的价值分析

探讨中考等大规模考试中学生数学问题提出能力考查的必要性与可行性，首先需要分析数学问题提出能力发展的必要性，为此，需要分析数学问题提出的价值，当然，更一般的就是问题提出的价值。

1.问题提出促进社会发展

纵观人类社会的发展史，一定程度上就是一个不断提出问题、解决问题的过程。人类社会的进步离不开科技创新，而每一个科技创新的成果都始于重大的现实问题，在问题的解决过程中产生新的方法和成果，形成新的发明创造，社会正是在问题的提出与解决的交替中不断进步。

2.问题提出利于个体发展

问题的提出活动被看作是一种创造性思维活动[3]，问题的提出需要人们对已有信息进行重新审视，从新的角度产生新的问题，这是一个创造性的过程。问题的提出活动，需要学生对已有情境或信息进行细致观察和缜密思考，它对于学生的观察能力、思维的灵活性、独创性以及流畅性都提出了很高的要求。学生在问题提出活动过程中，思维一直处于活跃状态，长期的问题提出活动能促进学生思维品质的提升。一个好的问题，是学生创造性、个性化思维活动的结果。因此，问题提出是培养学生创新能力的很好的载体，有利于学生个体的长远发展。

3.问题提出提升学习效益

教学中的问题提出活动实质上为学生提供了学习与思考的环境，它需要学生在给定情境的基础上，深入理解情境中的概念以及概念之间的关系。因此，问题提出能够促进学生对于有关知识以及它们之间相互关系的深刻理解。另外，问题提出与问题解决是伴生相随的，问题提出也促进了问题解决方法的形成。问题解决本质上是将问题从初始状态转变为目标状态，在此过程中，会对问题进行多次的重新表述，在多次处理问题的过程中就会出现问题提出[4]。如果在数学问题解决的过程中，对问题的重新表述或者问题提出的越好，那么解题者对于问题的解决将会越快。因此，数学问题提出能力的提升能够在一定程度上有效地提高学生解决问题的能力和学习效益。

4.问题提出的价值得到教师认可

为了了解我国初中生数学问题提出能力及其教学、测试现状，2021年，课题组编制了《初中数学问题提出情况的调查问卷(教师卷)》，通过有关骨干教师群发放，共收回来自江苏、山东、江西等14个省份的有效问卷1 752份。其中3道关于数学问题提出的重要性和价值的问卷数据如图1—3所示。

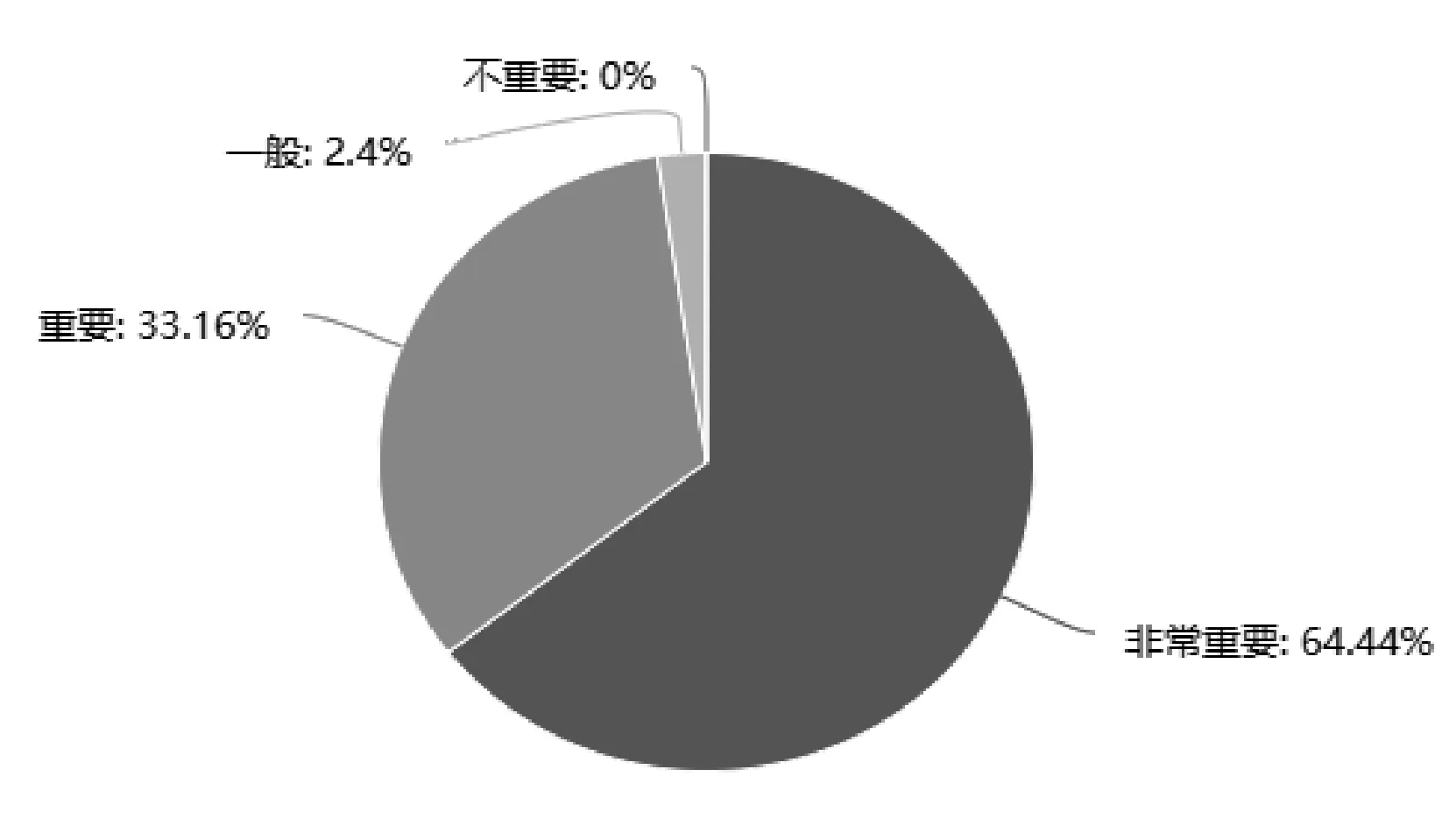
图1 教师认为数学问题提出的重要程度

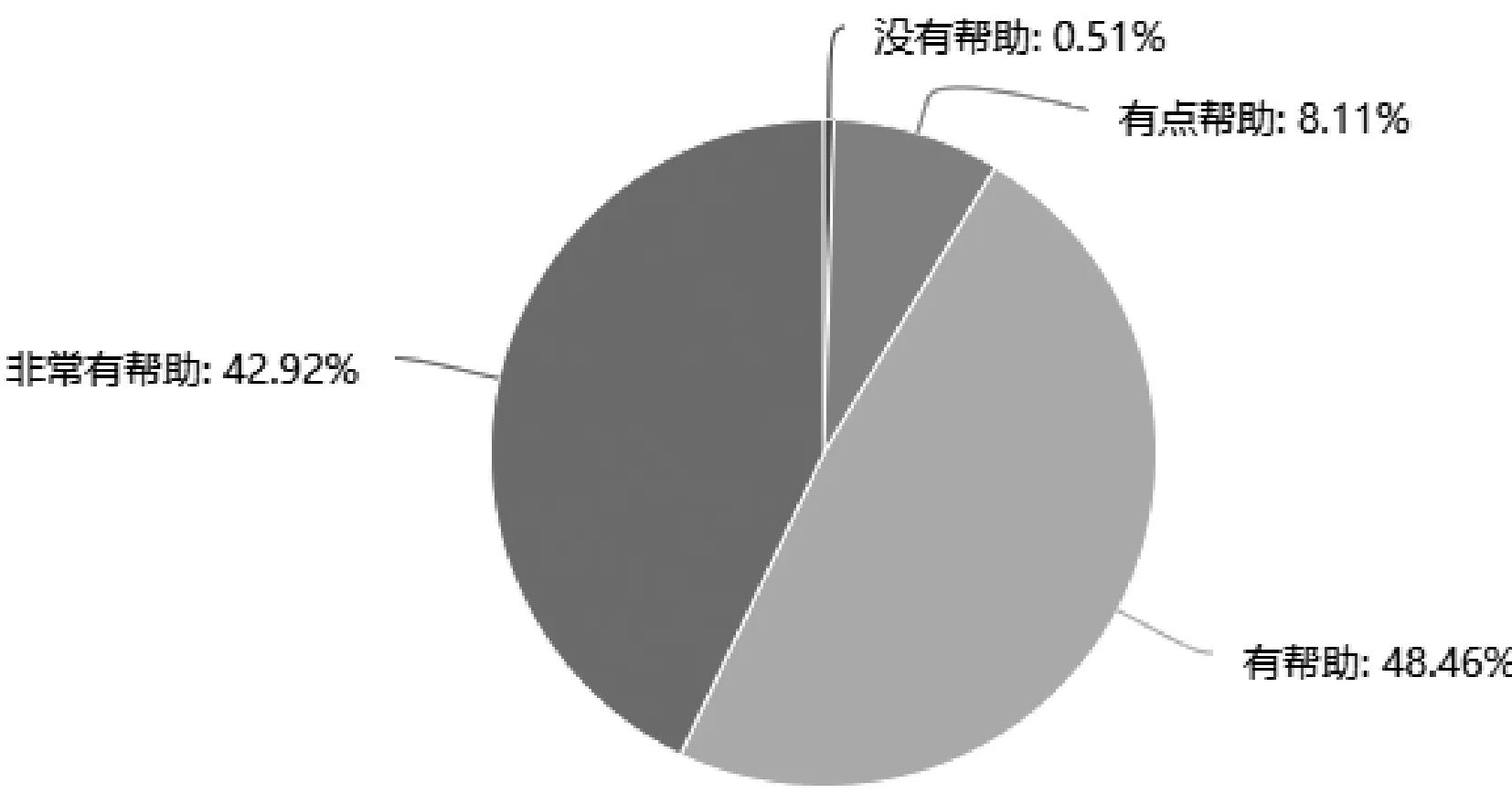
图2 教师认为数学问题提出对学生学习的帮助

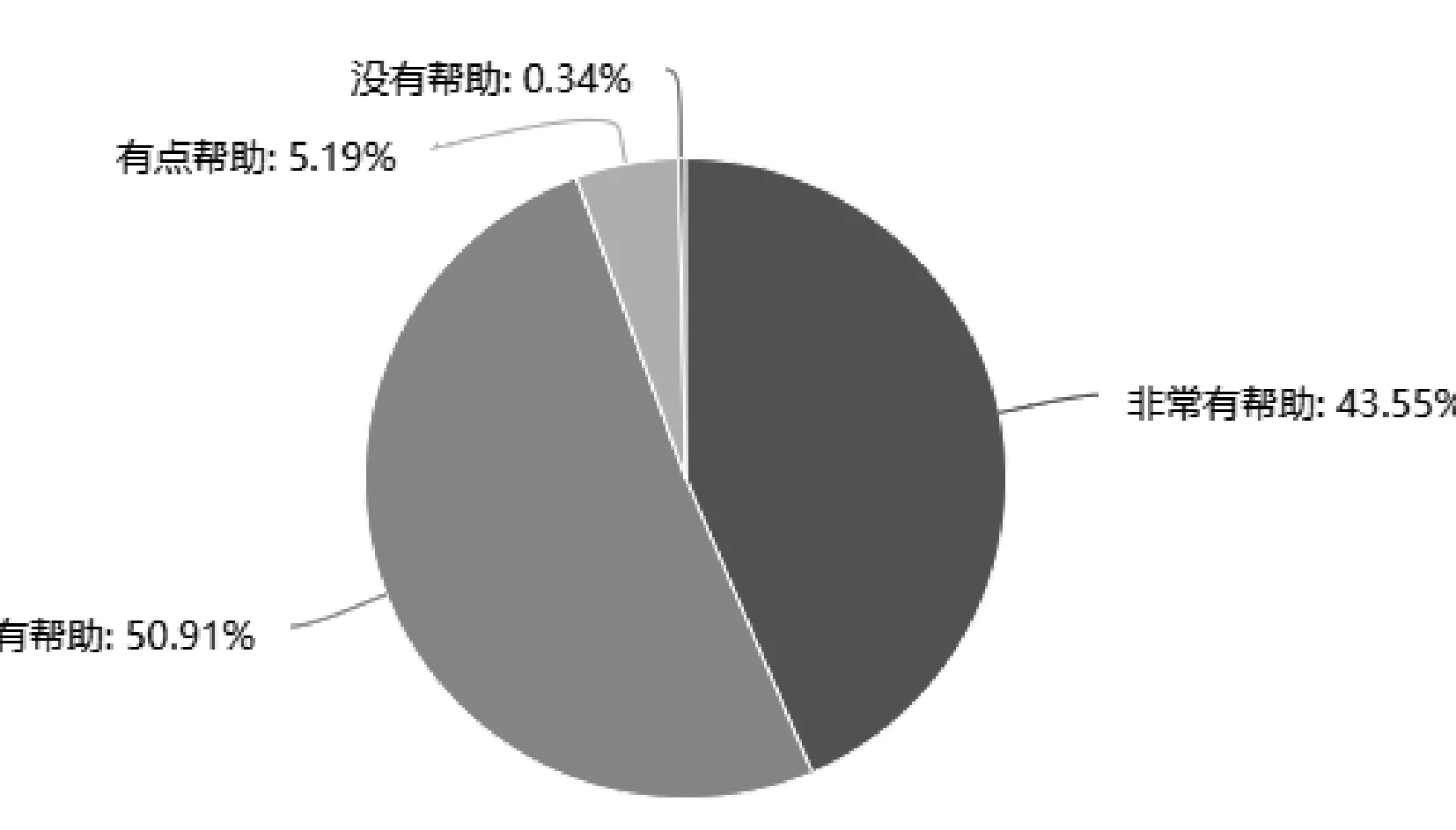
图3 教师认为数学问题提出对教学的帮助

数据表明，超过90%的教师认同数学问题提出的重要性，认为数学问题提出对于教师的教学和学生的学习均有帮助。因此，数学教学中应大力倡导对学生数学问题提出能力的培养。

二、大规模考试中数学问题提出能力考查的必要性

1.我国学生数学问题提出能力的现状

国内外多名学者对学生的数学问题提出能力进行了调查研究，研究结果均表明，当前我国学生数学问题提出能力偏低。如，2002年Cai和Hwang通过比较六年级和七年级的中美学生的数学问题提出能力，发现美国学生的数学问题提出能力优于中国学生[5]。曾小平、吕传汉和汪秉彝于2006年调查初中生“提出数学问题”的现状，选取贵州省5所中学初二的300名学生进行问卷调查，调查结果显示，学生主要从常规求解角度“提出数学问题”，创新精神和实践能力不够，总体来说学生的数学问题提出能力欠缺[6]。2013年，陈丽敏等人对辽宁省117名五年级小学生进行数学问题提出能力和观念的调查，结果表明,大部分学生能提出正确的数学问题,而提出创新性的、复杂程度高的数学问题存在困难，同时学生对学好数学问题提出,缺乏一定的信心[7]。Van Harpen 和 Sriraman 在 2013 年对美国和中国的优秀高中生进行数学问题提出测试，测试结果表明中国学生的数学问题提出能力较差[8]。2021 年，Yufeng Guo Jiajie Yan 和 Tongyu Men 以流畅性、灵活性和深刻性为评价指标，对中国大陆地区初中3个年级的学生进行数学问题提出能力的测试，研究结果表明，学生数学问题提出能力在三项评价指标上没有表现出整体上升的趋势，并且随着年级水平的提高流畅性分数下降且深刻性弱于流畅性和灵活性[9]。

2.学生数学问题提出能力偏低的原因分析

学生数学问题提出能力离不开日常教学的培养。为此，在编制的《初中数学问题提出情况的调查问卷(教师卷)》中，我们设置了3道问题以了解日常教学与考试中数学问题提出的情况，问卷数据如图4—6所示：

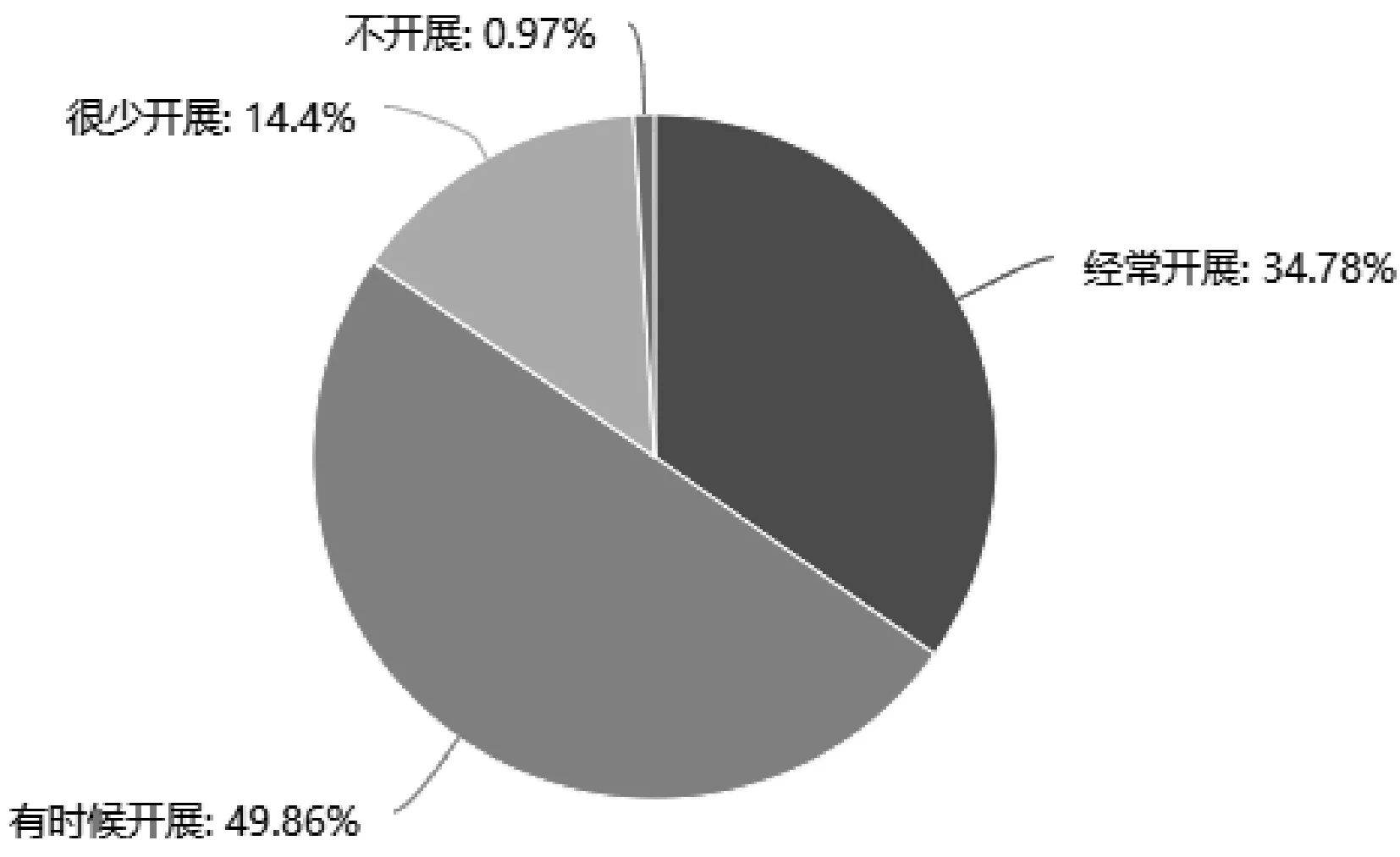
图4 教师开展数学问题提出教学的频繁程度

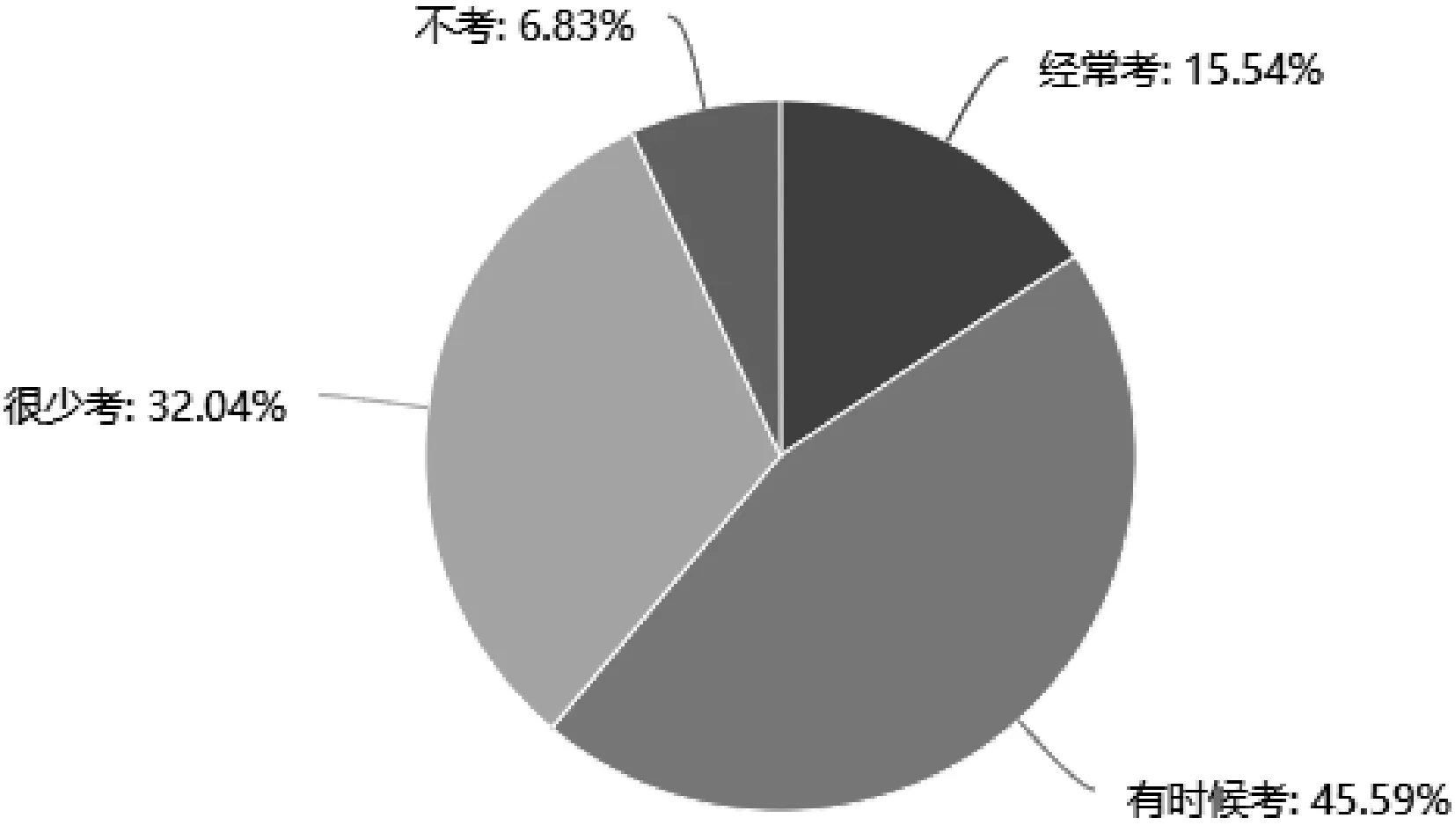
图5 教师在日常考试中考查数学问题提出的频率

图6 教师所在地的中考考查数学问题提出的频率

调查数据显示，65.22%的教师较少或不开展数学问题提出教学，超过80%的教师在日常考试中做不到经常考查数学问题提出，中考考查数学问题提出的频率也较低。总体来看，在教学和考试中，数学问题提出的实施情况并不乐观。

为进一步了解中考中数学问题提出能力考查的真实情况，我们查阅了2020年、2021年全国各省份的中考数学试卷301份，从中发现，试题以封闭的数学问题为主，只有极少数试卷中出现了开放性的试题，而并未发现与数学问题提出相关的试题。由此可见，各地的中考均未把学生的数学问题提出能力作为考查内容。

上述调研数据表明，学生数学问题提出能力的低下，根源在于日常教学中数学问题提出实践的欠缺和考试中问题提出能力考查的缺失。而数学问题提出实践的欠缺，一定程度上可能源于考试特别是大规模考试中对学生数学问题提出能力考查的缺失。

3.“以考导教”，提高学生数学问题提出能力

从当下的教育现状看，考试对于教师的教学与学生的学习具有极强的导向作用，考试的内容与形式直接影响着教师的教学方式，尤其是中考、高考这类大规模考试，作为升学考试，直接关系到学生下一阶段的学习。因此，一线教学中“以考定教”的观念盛行。在当下，“以考导教”不失为一种高效的教育调节手段。确立更为适切的考试目标，可以通过考试这一“指挥棒”引导一线教师开展更利于学生成长的教学。因此，在中考等大规模考试中加强对学生数学问题提出能力的考查，可以“以考导教”，促进数学问题提出能力的教学。调研数据也很好地支持了这一观点。在《初中数学问题提出情况的调查问卷(教师卷)》中我们特意设置了“若所在地中考考查数学问题提出，你是否进行数学问题提出的教学”这一问题，调查数据如图7所示：

图7 若中考考查数学问题提出，你是否进行数学问题提出教学

数据表明，如果教师所在地区中考考查数学问题提出，超过90%的教师会在日常教学中进行数学问题提出教学，这说明大部分教师认同“以考导教”，会顺应考试内容和考试形式调整自己的教学。因此，为提高师生对数学问题提出的重视程度和学生的数学问题提出能力，在大规模考试中考查数学问题提出十分必要。

三、大规模考试中数学问题提出能力考查的可行性分析

1.大规模考试中未进行数学问题提出能力考查的原因分析

(1)调查问卷分析

为调查中考中不考查数学问题提出的原因，本课题组在《初中数学问题提出情况的调查问卷(教师卷)》中设置了问题20：“目前大多数地区中考中不考数学问题提出，您认为原因是什么？(多选)”，以了解教师对目前中考当中很少考查数学问题提出的原因，同时设置了第21题“您参加过中考命题吗”，以对调查者的中考命题的经验加以区分，这两道题目调查数据交叉分析的统计结果如表1所示：

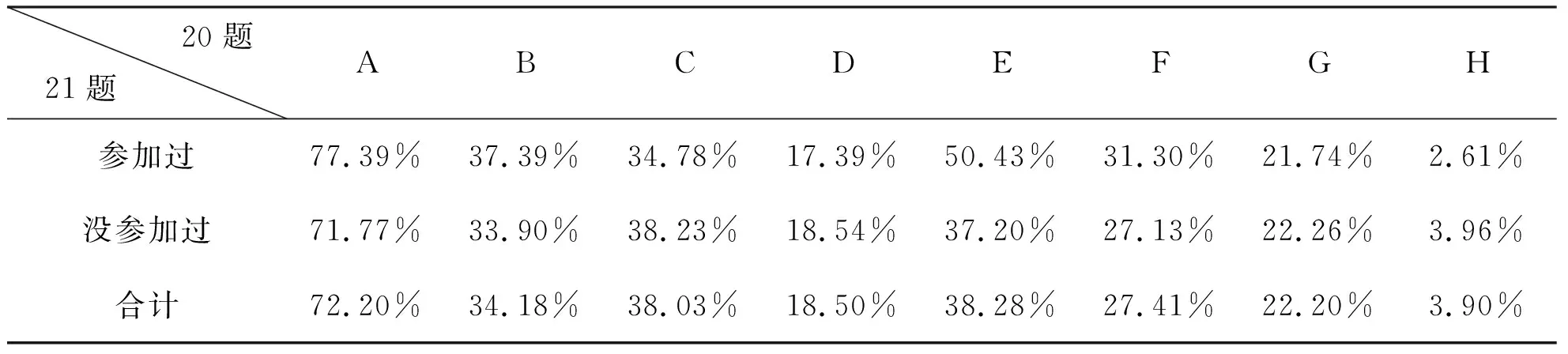
表1 调查问卷第20题和21题交叉分析

通过问卷结果分析，得出如下结论：

①超过70%的教师都认为“A.缺少客观的评分标准，改卷教师不能准确评分”是中考当中不考查数学问题提出的原因并且选择比重最大，可视为首要原因；

②其次选择较多的“E.阅卷时间长，阅卷工作量大”，虽然命题教师和非命题教师数据略有差异，但总体来看，选择该选项的人数排名第二。

③关于“B.教师在日常教学中不进行数学问题提出教学，考查问题提出会遇到教师的反对” “C.学生数学问题提出能力低下，考查问题提出会遇到家长的反对”“F.没有相关问题情境，命题工作人员没有相关经验”，分别是从教师教学、学生能力以及素材方面的不足进行考虑的，两类教师的选择比重相近，可视为第三梯度的原因。

④关于“D.数学问题提出考察不出学生的知识水平”“G.没有相关文件明确规定要考数学问题提出”是选择比重较低的选项，不是中考当中不考查数学问题提出的主要原因。

(2)中考命题人访谈分析

为深入了解中考等大规模考试中不考查数学问题提出能力的原因，课题组对南京市两位参加过中考命题的正高级教师进行访谈。两位教师均认同数学问题提出的重要性，认为数学问题提出能力的提高不论对于学生本身还是对于社会发展都具有重要影响，其重要性不容置疑。而对中考当中进行数学问题提出能力的考查，两位教师虽然都持赞成态度，但也表达了顾虑，认为存在很多障碍需要得到有效的解决，因此，在他们的中考试题命制实践中，也未敢尝试命制相关试题。他们认为，困扰问题提出能力考查的主要原因有：

其一，最重要的原因就是缺乏普遍认可的评分标准。数学问题提出作为开放性试题，并不像封闭性数学试题具有固定答案，因而亟须客观可持续的评分标准以保证评分的公平公正性。而目前虽然有不少学者研究了数学问题提出的评价框架，但并未形成统一的标准，因此在中考当中不便进行数学问题提出的考查。

其二，数学问题提出刻画学生数学水平的准确性有待验证。在多年的考试实践中，师生已经认可了常规数学试题，而对于数学问题提出类试题能否考查学生的数学水平尚存在疑问。

其三，阅卷工作量大。数学问题提出的评分过程较为复杂，阅卷工作量大，这在一定程度上增加了人力、物力和财力的消耗。

其四，数学问题提出的试题素材难找。中考命题时间短，本来日常教学中问题提出的素材就少，要在较短时间内找出合适的中考题较为困难。

(3)原因总结

综合问卷调查和访谈结果，对中考中不进行数学问题提出能力考查的主要原因如下：数学问题提出考查缺少客观的评分标准；数学问题提出的阅卷工作量大；命题人认为数学问题提出难以刻画学生水平；数学问题提出考查缺少出题素材；学生数学问题提出能力低下；教师在日常教学中较少开展数学问题提出教学。其中后3个原因主要是因为教学重视不够引起的，前述调查表明，如果中考中进行数学问题提出能力的考查，将会提高师生对数学问题提出的重视程度，随着日常教学中数学问题提出教学活动的常态化开展，学生的数学问题提出能力自然将得到较大幅度的提升，问题提出的素材也会随着教师的创造热情而大大丰富。第三个原因也只是命题者的一个担忧而已，已有研究表明，数学问题提出能力与学生的学习水平具有很高的相关性[10]。因此，我们认为，现阶段阻碍中考等大规模考试中数学问题提出能力考查的最主要的两个障碍是前两个，即：数学问题提出考查缺少客观的评分标准和数学问题提出的阅卷工作量大。

2.大规模考试中数学问题提出考查的可行性分析

只有切实破解以上阻碍大规模考试中数学问题提出能力考查的两个主要问题，大规模考试中进行数学问题提出能力考查才具有现实的可行性。为此，我们针对这两个问题提出两个对应的解决策略。

(1)构建评价框架，确保评价的准确性

关于数学问题提出能力考查的评价框架，有学者做过相关的研究，本文在借鉴他人研究的基础上，采用流畅性、灵活性、新颖性、深刻性、清晰性5个指标，构建了评价框架[11]，如表2所示。其中新颖性得分在“满意原则”的基础上采取加分制，新颖性加分S3以该题总分的25%左右为宜，其他四项得分加权求和。

表2 数学问题提出能力评价框架表

关于具体权重的确定，需要结合专家访谈和实际测试逐步完善。在力图通过大规模考试中数学问题提出能力考查促进师生重视数学问题提出能力教学的现阶段，首先应鼓励学生提出更多数量、更多种类的有效问题，从而打开学生数学问题提出的视界，因此，w1、w2所占权重不妨稍大一些；深刻性，本是考察所提出数学问题质量的一个重要指标，但考虑到在数学问题提出能力考查的初始阶段，学生提出问题时较少关注所提出数学问题的深刻性，学生也不易判断所提出数学问题的深刻性，因此，现阶段其权重占比可略小一些；至于问题表述的清晰性，并非考察学生数学问题提出能力的重点，其所占权重较小。基于上述考虑，可暂将w1、w2、w4、w5依次取值40%、30%、20%、10%。

为了检验该评价框架的稳定性和有效性，参照他人文献的基础上，研制了涵盖开放的生活情境、开放的数学情境和封闭的数学情境三类的测试卷(如图8)，并选取南京市某初中二年级两个平行班级的学生作为研究对象，在预测试的基础上进行了正式测试，收回有效测试卷110份。

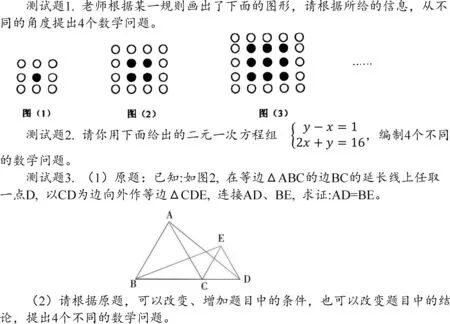
图8 初中生数学问题提出能力测试卷

测试卷编制经多次研讨、修改，并咨询5位一线数学教师的意见，测试卷得到了他们的认可。在正式测试之前进行了预测试以检验测试卷的有效性，因此测试卷具有较高的效度。

对于信度，本文首先按照评分标准，对于预测试时收回的15份测试卷进行评分，之后请某师范大学学科教学(数学)专业的研究生按照拟定的评分标准对这15份测试卷进行评分，运用SPSS26.0软件将两次评分的结果进行比较，比较结果如表3所示，皮尔逊相关系数r>0.96，因此说明两次评分是显著相关的，此测试卷信度较高，同时也说明了评价框架较为可靠，基于该框架的评价较为准确。

表3 不同评阅人评阅结果的相关性分析

此外，我们还进行了数学问题提出成绩与数学学业成绩的相关性分析，运用SPSS26.0软件，对被试学生的数学问题提出能力测试成绩与最近一次期中考试数学成绩进行相关性分析，分析结果如表4所示：

表4 数学问题提出能力测试成绩与数学学业成绩的相关性分析表

根据表4数据可以看出，学生的数学问题提出能力测试成绩与数学期中成绩的皮尔逊相关系数为0.588，其显著性值为0.000，小于0.05，说明被试学生的数学问题提出能力测试成绩与数学期中成绩具有显著的正相关性，这也进一步说明，学生数学问题提出能力可以反映学生的数学学业水平，“数学问题提出难以刻画学生水平”仅仅是部分教师的担忧而已。

2.研制评阅标准，减轻阅卷工作量

对于本文所建立的数学问题提出评价框架，可能有命题人员提出“在大规模测试中进行问题提出能力的评价，需要计算那么多达成度，会大幅增加阅卷者的劳动量”的担忧。实际上，在大规模测试中，命题的阅卷团队在试阅基础上可以制定出相对详细的评阅标准，在评阅标准中明确常规问题、新颖性问题的类型以及深刻度、清晰度的标准、示例，供阅卷人学习、参照，其后，阅卷人只要参照标准对学生提出的每个问题分别判断并进行勾选即可，具体勾选表如表5所示。

表5 阅卷勾选表

对学生提出的每一个问题，阅卷人只需依次判断该问题是否有效、是什么类型、深刻程度如何、清晰程度如何。如果是无效问题，不用进行后续判断；如果是有效问题，至多再进行3次判断，即在各备选的常规类型或新颖类型中勾选1项，在深刻性和清晰性中各勾选1项。大规模考试中，各地多采用机阅方式，这时可以设计简单的算法，教师仅仅进行勾选，赋分的计算工作可以完全交给计算机完成。如果尚未采用机器阅卷，可以让阅卷教师在阅卷勾选表下端增加一个合计栏，并按规则赋分即可。为了方便教师的赋分，还可以在各维度对应的汇总数下面直接给出对应的分值，减轻教师的计算量。

当然，具体工作量如何还需实践检验。研究中，我们对初二学生进行了数学问题提出能力测试，由于条件所限，采用线下阅卷，手工算分。评阅实践表明，平均评阅一道大题所需要的时间在3分钟左右。如果采用计算机赋分，还可以节约一定的时间。在中考这类大规模考试中，一道综合性的数学问题，阅卷时间大部分超过两分钟，因此，按照上述方法阅卷的时间并不算长。总之，通过事先研制相对详细的阅卷标准，对该题阅卷人员进行适当的专题培训，针对数学问题提出能力测试的相关试题的阅卷时间是可以得到有效控制的，因此，可以很好地解决数学问题提出能力考查中教师们对于阅卷工作量的担忧问题。

四、总结

总之，培养学生的问题提出能力十分重要，但我国学生数学问题提出能力偏低，其主要原因在于日常不进行数学问题提出的教学，也不进行数学问题提出能力的考查。调查表明，教师存在“以考定教”的观念，因此在中考等大规模考试中对学生进行数学问题提出能力的考查，“以考导教”，可以促进教师进行数学问题提出的教学，可见在大规模考试中考查数学问题提出十分必要。调查表明，中考等大规模考试中，命题人不进行数学问题提出能力的考查的最主要的两个担忧是：是否存在相对客观的评阅标准和阅卷工作量可能偏大。针对命题人员的这两个主要担忧，我们研制了相对客观的评价框架，研制了相对详细的阅卷建议并进行了实践检验。因此，在大规模考试中考查数学问题提出亦是可行的。为切实落实新课标理念，提高学生的数学问题提出能力，发展学生的“四能”，各地可以尝试在大规模考试中考查数学问题提出能力，进而“以考导教”以“撬动”各级学校和一线教师对学生数学问题提出能力的重视，从而将数学问题提出落实到日常教学和考试中。

由于本文研究中调查和测试的覆盖面还相对有限，各地在中考等大规模考试中进行问题提出能力的考查前，还可以结合当地实际进行更大范围的调研。期待更多考查学生“四基”“四能”的研究成果在大规模考试中出现，以切实促进学生获得良好的数学教育，使学生在数学教学中获得更好发展。