巧用逆向思维 妙解数学难题

◎翟翠莉

(广西桂林市国龙外国语学校，广西 桂林 541004)

逆向思维是对司空见惯的、似乎已成定论的事物或观点反过来思考的一种思维方式[1].实践表明，运用逆向思维解答初中数学习题有时能够实现简化解题步骤、减小运算量、提高解题正确率的重要目标，因此，在初中数学教学实践中，教师应将逆向思维纳入教学内容，通过教学活动的合理设计，使学习者认识到逆向思维的重要性以及在解题中的便利性，养成善于运用逆向思维解答数学习题的良好习惯，促进其解题能力以及数学学习成绩的进一步提升.

一、巧用逆向思维，解决函数求值问题

函数是初中数学的重点、难点，其中求值类问题在初中数学测试中较为常见.解答该类问题的常规思路是先从给出的已知条件入手进行推理，再逐渐向要求解的问题靠拢.而部分习题需要运用逆向思维来切入，即从要求解的问题入手通过分析构建与已知条件的联系，从而顺利解答.因此，教师在教学实践中应注重通过列举生活中的案例，使学习者加深对逆向思维的认识，掌握逆向思维在解答初中数学习题时的表现形式，如从问题出发、从给出的选项出发分析问题等都属于逆行思维的表现形式.同时，教师可以在课堂上展示经典例题，并与学习者一起分析习题考查的知识点、难在哪里以及如何运用逆向思维进行破题等，引导学习者主动思考.另外，为防止学习者知难而退，教师在讲解例题时应注重多给予学习者引导与启发，降低例题的理解难度，提升学习者听课体验[2].下面用此例题对此进行说明.

A.31 B.61 C.-21 D.-31

该题考查等价转化以及运用逆向思维解题的能力，难度较大.如从给出的已知条件入手正向推导，学习者不易找到解题思路.而基于已知条件进行变形，从要求解的代数式出发，通过拼凑逐渐向已知条件靠拢，解题的针对性会大大增加.当然期间还需要构造方程.为提高学习者的解题自信，教师应做好教学引导，帮助学习者更好地理解解题的关键点，使其通过认真听讲从而明白解题思路，掌握解题方法.

因为a，b，c分别为两个函数图像的三个交点的横坐标，故令(x-a)(x-b)(x-c)=0，则x3-(a+b+c)x2+(ab+ac+bc)x-abc=0，对照x3-4x2+1=0，可得a+b+c=4，ab+ac+bc=0，abc=-1，将其代入①可得16×(4-0)-3=61.故本题选择B项.

解题点评：遇到看似较为陌生、难以解答的习题，应考虑采用逆向思维，从要求解的问题出发分析如何将要求解的问题与已知条件关联起来，迅速找到思考方向.

二、巧用逆向思维，解决函数图像平移问题

函数图像平移问题是初中数学中常见的一类问题.解答该类问题可运用平移规律进行分析.但是部分习题具有一定难度，要求学习者不仅要理解平移规律，还要深刻理解函数图像与x轴之间的关系，并注重逆向思维的灵活应用.为此，教师应做好引导工作.一方面，教师要为学习者展示逆向思维的具体应用.如题干中给出平移后的函数表达式，要求平移前的函数表达式，此时就可以采用逆向思维反向思考平移方向[3].另一方面，由于初中数学习题类型较多，所以教师应引导学习者灵活运用逆向思维，尤其是对于选择题，可从给出的选项入手逐一分析，再验证推理得出的结果是否符合题干描述，从而做出正确判断.下面用此例题对此进行说明.

例2在坐标平面上移动二次函数y=-(x-2018)(x-2020)-2的图像，使其和x轴交于两点，且两点的距离为两个单位，则以下移动方式可行的是( ).

A.向上平移两个单位 B.向下平移两个单位

C.向上平移一个单位 D.向下平移一个单位

该题为选择题，可采用逆向思维，从给出的选项入手，运用函数图像平移规律逐一进行判断.需要注意的是要搞清楚题干中的函数表达式与一般表达式之间的关系.针对该题给出的四个选项中只有“上移”和“下移”，再结合函数平移规律可知，上下平移仅影响函数的常数项部分，因此，该题不需要将函数表达式转化为一般形式，直接运用平移规律判断即可，否则就会陷入复杂的运算中.同时，结合所学以及经验可以判断出y=-(x-2018)(x-2020)和x轴的交点横坐标分别为2018和2020.

A项，向上平移两个单位后得到的二次函数为y=-(x-2018)(x-2020)，图像和x轴的交点横坐标分别为2018和2020，两点距离为两个单位，符合题意；B项，向下平移两个单位得到的二次函数为y=-(x-2018)(x-2020)-4，图像和x轴两个交点的距离一定小于两个单位，不符合题意；同理C，D两项也不符合题意.故本题选择A项.

解题点评：要解决初中二次函数图像平移类问题，学习者应具备良好的逆向推理意识，要么将平移后得到的图像作为推理的切入点；要么根据习题类型，采用有针对性的逆向推理方法.如遇到选择题可分析其给出的选项，通过排除找到正确的选项.

三、巧用逆向思维，解决不等式组相关问题

求解一元一次不等式组是初中生必备的能力[4].在学习初中数学的过程中，学习者通常习惯于直接求解所给不等式组的解集，但是部分习题却给出不等式组解集，要求学习者判断不等式组中有关参数的取值范围，并以此为基础解相关方程[5].该类问题的难度较大，能很好地检验学习者对所学知识的理解程度.解答该类问题需要逆向运用解不等式组的思路，并结合数轴准确判断未知参数的取值范围.另外，解分式方程时不仅要在解上满足要求，还需保证分式方程有意义，这就要求学习者在解题时考虑全面，尤其在判断最终结果时不能顾此失彼.为提高学习者解答不等式组类难题的正确率，教师在讲解相关例题时应注重引导学习者积极动脑分析，认真揣摩解题思路，体会逆向思维的具体应用过程.下面用此例题对此进行说明.

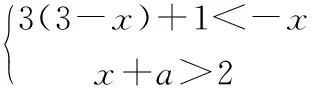
A.1 B.2 C.3 D.4

根据题意先解关于x的一元一次不等式组，采用逆向思维，再结合给出的解集得到a的取值范围，而后解分式方程进行分析.正确运用逆向思维是提高解题正确率的关键.众所周知，解一元一次不等式组的常规做法是先分别求出各一元一次不等式的解集，而后按照相关法则确定最终解集，而运用逆向思维时应注重反过来思考相关法则，尤其应重点分析等号能否取到.

由3(3-x)+1<-x，解得x>5，由x+a>2，解得x>2-a.由题可知不等式组的解集为x>5，如图1所示：

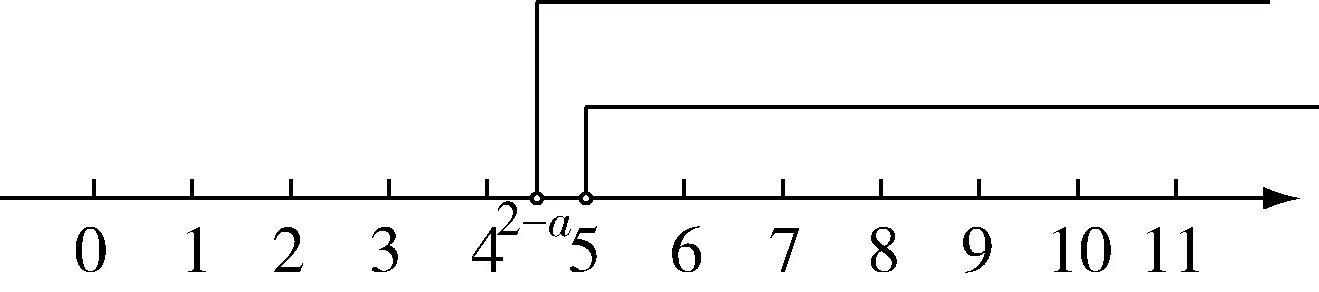
图1

解题点评：给出不等式解集求不等式组中的某一个参数的取值范围，可先采用常规方法解出各不等式的解集，而后结合给出的最终解集逆向思考，再结合数轴进行验证，构建正确的不等式关系，从而找到要求的参数的取值范围，在此基础上完成问题的解答即可.

四、巧用逆向思维，解决代数式求值问题

代数式求值问题在初中数学中是非常常见的一类问题.不同习题考查的知识点不同，应用的解题思维也有所区别.该类问题的常规求解思路是对要求解的代数式进行适当的变形与整理，使其含有已知条件中的代数式，而后将已知条件中的代数式的值代入即可[6].但是部分习题给出的代数式较为特殊，采用常规思路难以构建已知条件与要求解代数式之间的关系.针对该类问题学习者应认真分析给出的已知条件，积极联系所学知识，采用逆向思维构建对应方程，加深对相关参数关系的认识.如在整理已知条件时，得出两个参数和与积的值，此时可逆向运用根与系数的关系构造一元二次方程.在初中数学教学过程中，为使学习者理解并掌握这一解题思路，深刻体会逆向思维的具体应用，教师应重点为学习者做好例题讲解，通过设问逐步引导学习者向着正确方向思考，确保问题得以顺利解决.下面用此例题对此进行说明.

例4已知xy+x+y=28，x2y+xy2=160，则x2+y2的值为________.

该题的已知条件较为简洁，考查整体思维以及逆向思维的灵活应用，难度较大.很多学习者看到该题后一时难以找到正确的解题思路.事实上，解答该题需要联系一元二次方程中根与系数的关系逆向推理出对应的一元二次方程.同时，该题较为特殊的是需要采用逆向思维构造三个一元二次方程，并结合一元二次方程的根的判别式对求解的参数进行合理取舍，因此，教师讲解该题时应要求学习者做好听课记录，认真揣摩解题过程，多问为什么.真正理解与掌握了解题方法，以后遇到类似问题就能够迅速地找到解题思路了.

由x2y+xy2=160，可得xy(x+y)=160，而xy+x+y=28，将xy和x+y分别看成一个整体，两个等式即可对应一元二次方程的两根之积和两根之和，则其对应的一元二次方程为x2-28x+160=0，容易得到x1=8，x2=20.当xy=20，x+y=8时，其对应的一元二次方程为x2-8x+20=0，此时Δ<0，舍去；当xy=8，x+y=20时，其对应的一元二次方程为x2-20x+8=0，此时Δ>0，符合题意.∴x2+y2=(x+y)2-2xy=202-2×8=384.

解题点评：遇到有关两个参数或代数式的乘积与和的问题时应冷静分析，联系所学的一元二次方程中的根与系数的关系，通过逆向分析问题构建对应的一元二次方程，从整体上求出相关参数的积与和，而后联系所学知识得出最终结果.

五、巧用逆向思维，解决求解参数值问题

求解参数具体值是初中数学的热门考点.虽然采用正向思维能够解决大部分习题，但是一些习题则需要运用逆向思维对给出的已知条件进行巧妙转化，以更好地揭示参数之间的内在联系，为顺利求解出最终结果奠定基础[7].实践表明，运用逆向思维解答该类问题往往需要学习者能够逆向运用相关计算公式、规律等，因此，为使学习者熟练运用逆向思维解答该类问题，一方面，教师在讲解相关计算公式、规律时应引导学习者参与到公式、规律的推理中，使其搞清楚计算公式、规律的来龙去脉，而非死记硬背[8].同时，教师在课堂上应多设计判断正误类的问题，使学习者不仅能够正向推导和运用计算公式、规律，还能逆向运用.另一方面，教师还应通过对相关习题解答过程的讲解，使学习者更好地掌握运用逆向思维解答求参数值难题的具体思路以及应注意的细节，避免其在以后的运用中走弯路.下面用此例题对此进行说明.

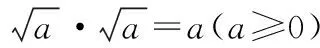
解题点评：遇到根式相关的问题时应考虑采用逆向思维，通过相关计算公式的逆向运用对给出的代数式进行因式分解，将复杂问题简单化，再结合相关解题经验，抽丝剥茧，逐步突破问题.

六、巧用逆向思维，解决求解参数范围问题

求参数取值范围类问题是初中数学测试以及中考的常考内容.因不同习题的设问角度不同，所以考查的知识点以及应用的解题思维也存在一定差别[9]，其中部分习题就主要考查学习者对于逆向思维的应用.该类问题虽然能够采用正向思维解答出来，但是计算是非常复杂的，在测试中是尤其不可取的.为高效地解答该类问题，应从要求解问题的反面出发，通过逆向思维达到顺利解题的目的.在教学实践中为使学习者亲身体会如何运用逆向思维解答求解参数范围问题，体会运用逆向思维解题的便利，教师应为学习者做好例题的筛选与讲解，尤其要注重预留空白时间，要求学习者通过思考讨论快速找到要求解问题的反面.如至少有一个条件成立的反面为所有条件均不成立，能够理解这一点便不难解答出相关习题.下面用此例题对此进行说明.

例6若关于x的方程(x2-2x+k)(x2-3x+k+4)(x2-4x-k+8)=0有实根，求k的取值范围.

该关于x的方程较为复杂，涉及三个代数式.从理论上来讲，若三个代数式的乘积为零则至少有一个代数值的值为零.如采用常规思路需要考虑很多种可能，计算复杂.而采用逆向思维，能大大地简化解题步骤并减小运算量.通过分析不难得知，上述问题的反面为所给方程无实根，则对应的三个代数式的值均不为零.运用根的判别式可很快求出k的取值范围，而后取其反面就是最终答案.

解题点评：解答初中数学习题时，当需要考虑的方面非常多时，可采用逆向思维，从要求解问题的反面入手，求解出问题答案，而后对得出的结果再取反面，这便是问题的正确答案了.如此能够大大地减小运算量，促进解题效率的有效提高.

综上所述，初中数学习题情境复杂多变，其中部分习题如采用常规方法来解反而会走弯路，此时应注重逆向思维的灵活应用.为使学习者更好地认识到逆向思维的重要性，提高其在解题中的应用灵活性，教师应在做好逆向思维理论基础知识系统讲解工作的基础上，优选、精讲典型例题，使学习者认真体会逆向思维与传统思维方式的不同，把握逆向思维适合应用的习题类型以及运用的注意事项，提高其应用水平.