对一个条件概率问题的思考与变式
张洪源 (河北省唐山市第一中学2020级16班 063000) 指导教师 王筱颖
条件概率是高中数学的重要知识点,掌握条件概率的概念和应用是学习的重点.近日,《天才基本法》这部电视剧在各大平台热播,剧情中出现了许多有趣的数学题目,其中的一个条件概率问题引发了笔者的深入思考.
1 情景
有三个完全相同的盒子,第一个盒子里面装了2个红球,第二个盒子里面装了2个蓝球,第三个盒子里面装的是1个蓝球和1个红球.
2 问题与分析
从三个盒子中随机选择一个盒子,从里面拿出一个球,发现球是红色的.这个盒子里剩下的那个球也是红球的概率是.
为了便于分析,我们将题目中各个盒子中的球进行编号.设第一个盒子中的两个红球分别为A1和A2;第二个盒子中的两个蓝球分别为B1和B2;第三个盒子里的红球为A3,蓝球为B3.
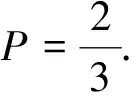

评注此问题属于条件概率中的“有序”问题,和著名的“三门问题”原理类似,解决问题时一定不能盲目依靠直觉求解.
3 变式
变式1 从三个盒子中随机选择一个盒子,发现盒里的两球中有红球.这个盒子里的两球都是红球的概率是.

评注此问题属于条件概率中的“无序”问题,如果采用列举法,一定要注意A3B3和B3A3两个事件都需满足已知条件.
变式2 从三个盒子中随机选择一个盒子,从里面拿出一个球,发现球是红色的.这个球来自第一个盒子的概率是.

评注此问题属于条件概率中的后验概率问题,即“执果寻因”,可以使用贝叶斯公式直接求解.
变式3 从三个盒子中随机选择两个盒子,分别从中拿出一个球,发现拿出的球里有红球.拿出的两球是一红一蓝的概率是.


评注此类问题事件情况数较多,需要对事件进行合理拆分,结合全概率公式求出所需事件概率.如果遇到求复杂事件的概率时,可以尝试使用“正难则反”的方法,先求出其对立事件的概率,再得到所求概率.
以上是笔者对于一个条件概率问题进行的思考与变式,希望能对各位读者学习、理解此类问题有所帮助.
——两球与墙壁三者间的碰撞次数与圆周率π间关系的讨论

