刷新思维突破“图形与几何”教学思维定式
浙江平湖市乍浦天妃小学(314201)沈勤
一、问题与原因分析
“图形与几何”对小学生几何思维能力的培养有着不可替代的作用。小学生的认知、心理、思维等方面较为特殊,这给他们学习“图形与几何”带来了许多障碍(见表1)。
笔者从儿童的知识与经验出发,以90名学生为研究对象,分析学生出现的错误,找出了引起学生学习“图形与几何”思维定式的问题所在(如表1)。
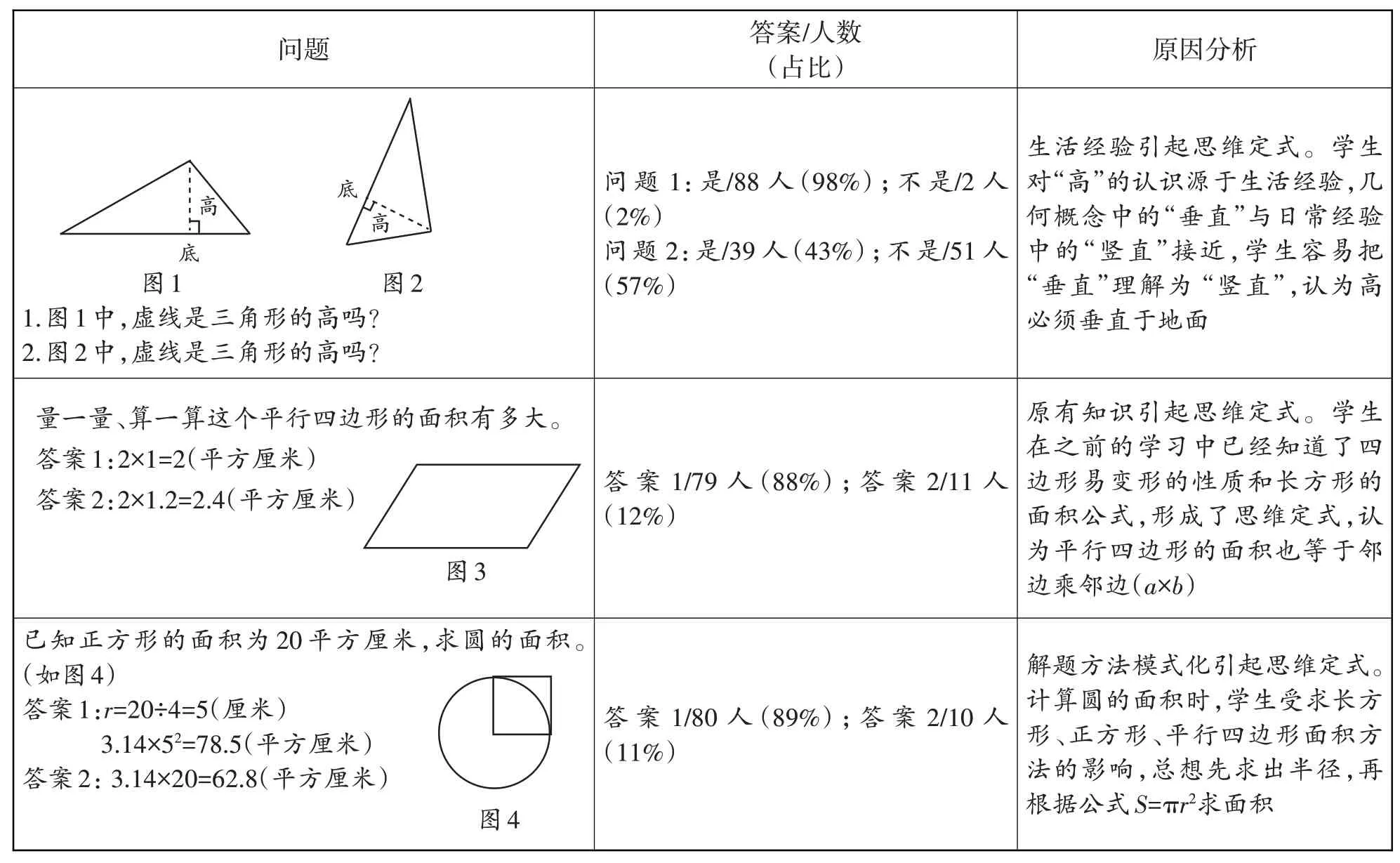
表1 小学生“图形与几何”解决问题的现状调查与原因分析
二、对策和措施
为了改善学生在学习“图形与几何”中存在的生活经验、原有知识、方法模式束缚几何思维的现象,笔者想出了经验刷新、对比刷新、变式刷新三大教学对策,走出了一条可行、灵动的突破“图形与几何”教学思维定式的道路。
1.经验刷新——突破生活经验对图形概念的负影响
现实生活中有许多几何图形,学生在生活中积累了一定的几何经验。但当生活经验和图形概念不同时,学生要巧借生活经验、生活原型来刷新原有经验,厘清生活经验与图形概念的区别,突破生活经验对图形概念的负影响。
(1)调用生活经历,明确要素
数学源于生活又服务于生活。教师可以提供恰当的、精心选择的生活原型,调动学生的生活经验,让学生感悟其中的道理,建立正确的表象,丰富对图形概念的认识。
如教学人教版教材六年级下册“立体图形总复习”时,让学生利用一张长方形纸折一折几种立体图形(如图5)。通过实践操作,学生发现直棱柱不仅体积可以用底面积×高的通用公式来计算,它们的侧面积也可以用底面周长×高的通用公式计算,从而打破学生习惯用常用公式求长方体和正方体表面积的思维定式。
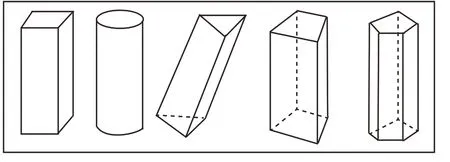
图5
(2)借助生活原型,排除干扰
数学模型源于生活原型,教学中,教师要引导学生充分经历从数学原型到数学模型的知识创造过程,消除生活原型对概念学习的干扰,消除事物非本质属性的干扰,深化学生的数学理解。
如“三角形的高”是教学的难点,教学时,教师将“两个人比高矮”的情境换成“两个三角形比高矮”,既保留了生活原型中“水平为底、竖直为高”这一关键特征,又满足了“三角形的高”的教学要求,让学生从“水平方向的底、竖直方向的高”这一生活原型中,抽象出“垂直”这一本质特征。在做出“水平方向的底、竖直方向的高”以后,学生旋转三角形,感知高不仅是从上往下垂直于水平面的,还有各种不同方向的,从而使学生对高的认识实现由生活原型到数学概念的飞跃。
2.对比刷新——打破原有知识对图形表象的负迁移
认知水平的提高得益于深刻的反思,有了对比,反思会更深刻。因此,教师在教学中要充分挖掘教材,开展新旧知识对比、易混知识对比,让学生真正了解新旧知识间的区别与联系,避免已有知识对图形表象的建立产生副作用。
(1)对比新旧知识,凸显图形本质
新旧知识对比是进一步优化思维的过程,这样可以达到沟通新旧知识、建构知识体系的目的,更好地发展学生思维。
学习新知前比一比——引入新知前,教师要深入剖析教材,让学生比较新旧知识,从而明确新旧知识之间的区别与联系,为正确理解图形概念打下坚实的基础。
如教学人教版教材“角的初步认识”时,教师可设计一个摆角活动,让学生用三根小棒摆一个学过的图形,再让学生拿走任意一根,然后观察它变成了什么图形。(如图6)摆角活动加强了新旧知识之间的联系。学生对三角形与角进行了有效的比较,找到它们的异同,理解了新知识角的本质特征:一个顶点,两条边。
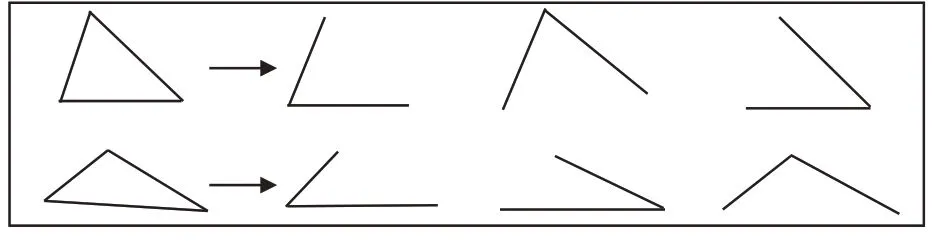
图6
学习新知后比一比——学习新知后,让学生比较新知识与旧知识,进一步了解新旧知识之间的联系。
如教学人教版教材“梯形的面积”时,在学生探究出梯形的面积公式后,开展探究“梯形上底变化会引起什么变化”的活动,让学生思考:当上底与下底一样长时,变成了什么图形?当梯形上底为0时,变成了什么图形?从而让学生更加了解长方形、正方形、平行四边形、三角形、梯形面积公式间的联系,有效防止学生产生思维定式。
(2)对比易混知识,构建图形表象
不少图形知识的意义相近却不同,它们之间互有联系又有所区别,容易混淆。教学时,通过对比易混知识环节,让学生开展“求同”或“辨异”比较,使易混知识在其头脑中清晰化。
用“比”破难点——学生易受思维定式的影响,面对熟悉的概念、图形时会出现思维僵化。教师可以在教学中设计对比活动,促进学生突破认知难点,避免学生受思维定式的影响。
如教学“角的初步认识”时,设计三角板比大小活动:出示三块形状一样、大小不同的三角板(如图7),让学生进行比较。
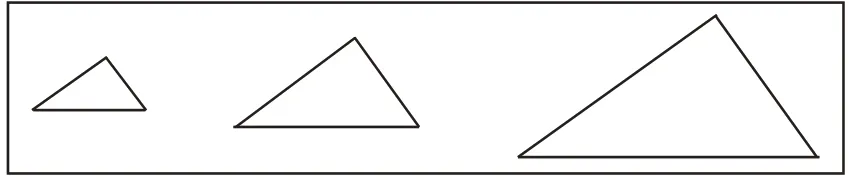
图7
比较一:这三块三角板有什么不同之处?有什么相同点?
比较二:三块三角板中,你觉得哪块的三个角大一点?
通过实际操作、比较、演示等手段,引导学生发现三个三角形的形状相同,对应角的大小也相同,但面积不同,从而使学生真正跳出一维长度和二维面积来认识决定角的大小的因素。
借“比”提思维——学习不能只停留在机械模仿的层面,教师可以设计通过比较揭示规律性知识的活动,让学生借助比较获取新知识和新技能,真正让学生在比较中提升思维能力。
如教学“角的初步认识”时,设计数角比大小活动:在一个角中添上一条线(如图8),就变成了几个角?哪个角最大?
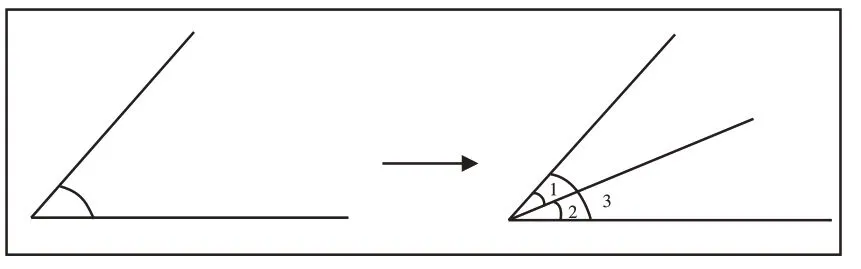
图8
学生通过电脑演示,明确一个顶点和任意两条边都可以组成一个角,三条边就可以组成三个角:∠1、∠2、∠3。再比较这三个角,学生想到了一种比较角的大小的重要方法——叠合法:因为∠1和∠2合起来正好和∠3重合,所以∠3最大。还有学生用∠1+∠2=∠3得出∠3最大,初步产生了角可以“相加”“相减”的观念。这样的比较活动使抽象的几何知识变得更加直观、具体,打破了学生对“角的大小与边的长短有关”的思维定式,真正提升了学生的几何思维。
3.变式刷新——突破单一思维对几何思维的负效应
变式刷新要求教师在原有教材练习的基础上进行创意练习设计,通过玩“多”、玩“逆”,引导学生从不同角度思考问题,打破思维定式,发展学生的求异思维、发散思维、逆向思维。
(1)玩“多”,凸显多样思维
玩“多”是指抓住思维训练这条主线,适当改变问题情境或思维角度,引导学生从不同途径寻求解决问题的方法,凸显多样思维。
常规练习新颖化——把常规练习改编成多样习题,为学生提供广阔的思维空间,培养思维的广阔性。
如:求图9中草地的面积。学生最常想到的方法是用标准图形面积减去小路面积,通过常规练习新颖化,激活了学生的几何变换能力,把较复杂的图转化为简单的图。
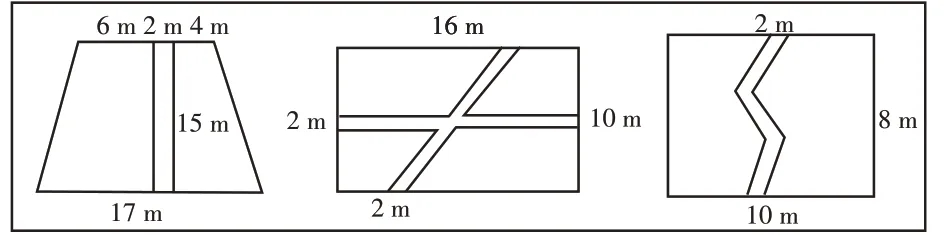
图9
单一练习多样化——把单一的练习进行多种变式,层层递进,从而削弱思维定式对学生的干扰。
如:下面三幅图(如图10)中正方形的面积都是20 m²,每个圆的面积各是多少?这一练习引导学生进行多维思考,深化了他们对圆与正方形面积比的理解,真正关注面积公式的本质,打破了套用公式的思维定式。
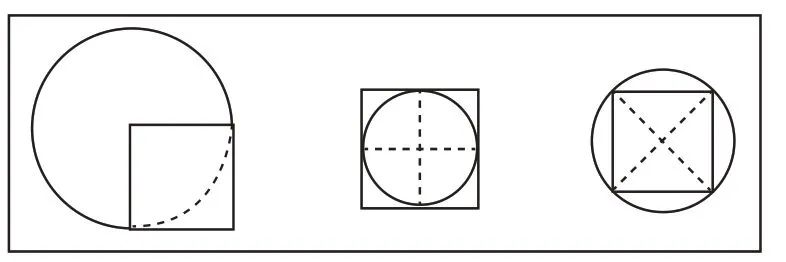
图10
(2)玩“逆”,凸显逆向思维
玩“逆”是指为实现某一创新或解决某一因常规思路难以解决的问题,以逆向思维进行求解的过程,引导学生从正向运用知识转向逆向运用知识,培养学生的逆向思维能力。
利用公式逆推图形——从图形推导出公式,是一个从直观到抽象的过程,在学生对转化方法应用较为熟练后,教师可以设计从公式逆推图形的练习。
如:你能根据三角形面积公式的三种不同形式,分别画出三角形吗?(答案如图11)
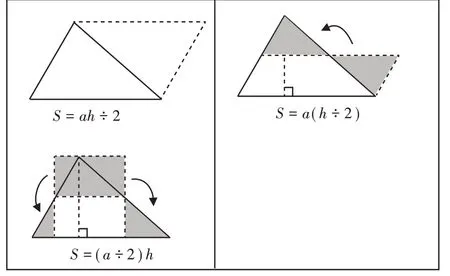
图11
①S=ah÷2 ②S=a(h÷2)③S=(a÷2)h
改变条件逆向练习——学生运用面积公式进行解题,容易形成思维定式,教师通过改变问题与条件设计逆向练习,可以锻炼学生思维的灵活性。如这个练习:靠墙边用篱笆围成一个花坛,用去46 m的篱笆,求花坛的面积。(如图12)
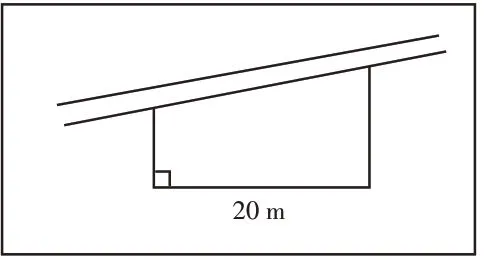
图12
总之,当我们走出了思维定式,就会创造许多奇迹。从飞鸟可以联想到飞机,从蝙蝠可以联想到电波,从苹果落地可以悟出万有引力定律……教师在教学“图形与几何”时,要全面把握教材,利用各种条件、采用多种手段,引导学生通过多种感官对图形进行感知,刷新思维,突破思维定式,形成正确的图形表象和清晰的几何概念,使学生的思维从单一、固化、定向逐步向丰富、灵活、多向发展,从而提升学生的“图形与几何”思维能力,提高学习“图形与几何”的效力。

