近十年高考数学全国卷“平面向量”试题分析及教学思考*

项丽红 逯彦周

(甘肃省永登县第六中学 730300)

向量理论具有深刻的数学内涵和丰富的物理背景.[1]向量具有几何与代数双重属性，是沟通几何与代数的桥梁，同时高中的平面向量知识是进一步学习高等数学的基础.2012年—2021年十年间，我国高考数学命题经历了考试大纲、课程标准并存指导，到终止考试大纲，完全依据课程标准的过程.[2]对这十年高考数学全国卷中的平面向量试题在宏观层面从类型、题数、分值、难易程度进行统计分析，在微观层面从试题考查知识点、融合其他知识点进行统计分析，并以此为依据对教师教学提出一些建议.

1 十年高考全国卷平面向量试题宏观统计分析

以2012—2021十年高考全国卷(共29套)中的平面向量试题(共38道)为研究对象，将38道平面向量试题从宏观层面按类型、题数、分值、难易程度进行统计，结果如表1所示.从类型看，38道题目中，选择题共20道，填空题共14道，解答题共4道，占比分别为52.6%、36.9%、10.5%.从题数看，29套试卷中，21套试卷的平面向量试题均为1道，占比72.4%，分值为5分；4套试卷的平面向量试题均为2道，占比13.8%，分值为10分；3套试卷的平面向量试题均为2道，占比10.3%，分值为17分；仅有1套试卷中平面向量试题为3道，分值为22分.从难易程度看，38道试题中，难度为易、中的试题分别为20道、12道，占比分别为52.6%、31.6%，较难题为6道，占比15.8%.

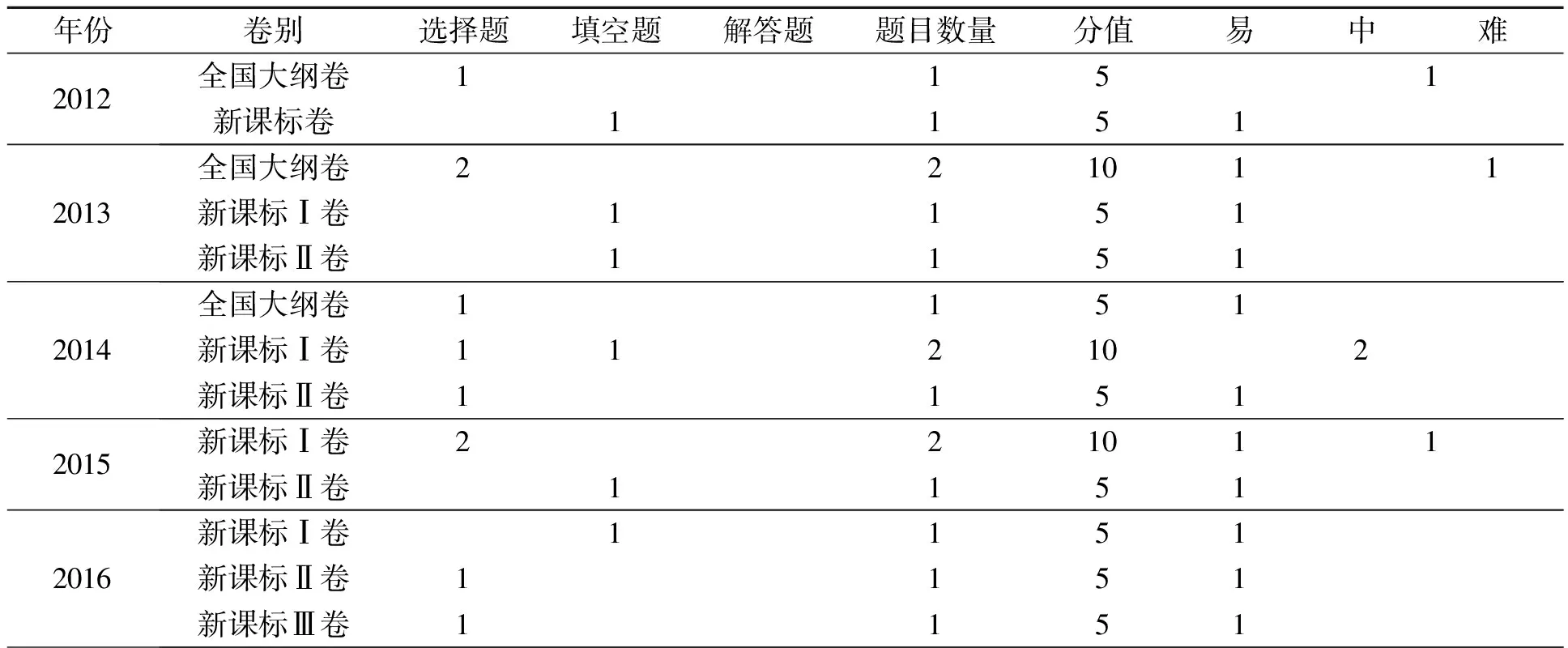
表1 2012—2021全国卷平面向量试题统计

2 十年高考全国卷平面向量试题微观知识点分析

2.1 试题考查知识点统计分析

将平面向量试题考查知识点按照线性运算及其几何意义、向量平行、平面向量基本定理、平面向量的数量积及模与夹角、向量垂直、平面向量坐标运算进行统计(只要试题有体现就计数)，结果如表2所示.由表2知，38道试题中，考查线性运算及其几何意义、平行、垂直、平面向量基本定理、数量积及模与夹角的试题分别有5道、4道、5道、4道、14道，占比分别为13.2%、10.5%、13.2%、10.5%、36.8%；考查线性运算、平行、垂直、数量积及模与夹角的坐标运算的试题分别有10道、4道、6道、17道，占比分别为26.3%、10.5%、15.8%、44.7%.总的来看，考查线性运算、平行、垂直、数量积及模与夹角的分别有15道、8道、11道、31道，占比分别为39.5%、21.0%、29.0%、81.5%.

表2 2012—2021全国卷平面向量试题考查知识点统计

在38道平面向量试题中，28道只考查了平面向量内容的知识点，没有与其他知识融合,且绝大多数试题考查知识单一，属于简单题.如：

例1(2021年全国甲卷第14题)已知向量a=(3,1),b=(1,0),c=a+kb.若a⊥c，则k=.

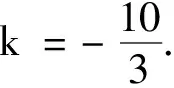
例2(2017年全国Ⅰ卷第13题)已知向量a,b的夹角为60°，|a|=2，|b|=1，则|a+2b|=.

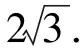
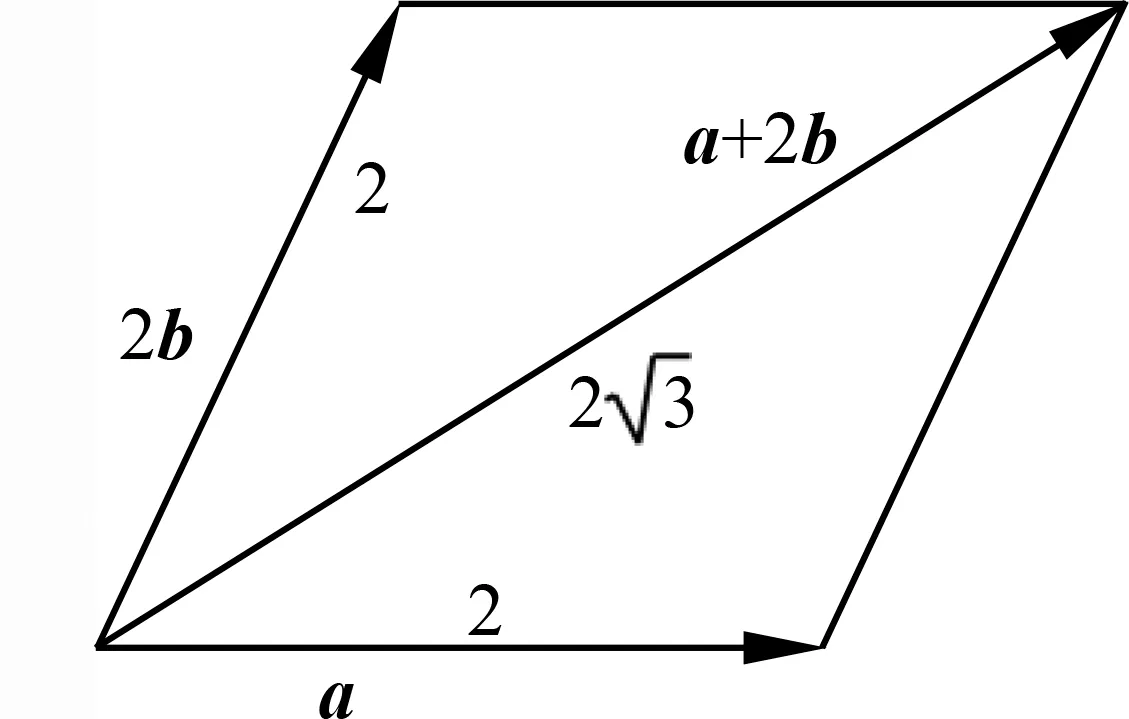
图1

2.2 试题融合其他知识点统计分析

平面向量与其他知识点的融合具有明显的倾向性(表3)，38道平面向量试题中，10道融合了其他知识，其中与圆锥曲线的融合包括圆、椭圆、双曲线与抛物线，共有6道，其余4道是与三角函数及解三角形、函数、数列融合.

表3 2012—2021全国卷平面向量试题交汇知识统计

当平面向量试题融合其他知识时，多考查平面向量的坐标运算，多数为数量积及模与夹角、垂直的坐标运算.如：

例3(2021年新高考Ⅱ卷第10题)已知O为坐标原点，点P1(cosα,sinα)，P2(cosβ,-sinβ)，P3(cos(α+β),sin(α+β))，A(1,0)，则( )

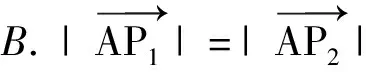
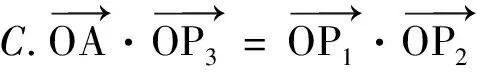
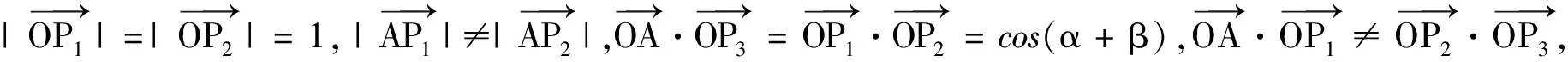
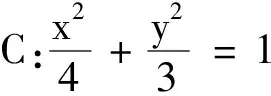
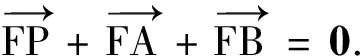
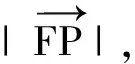
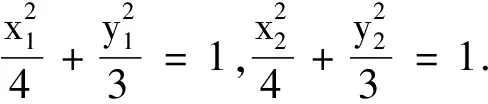
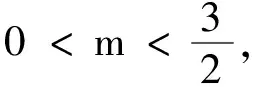
(2)由题意得F(1,0)，设P(x3,y3)，则(x3-1,y3)+(x1-1,y1)+(x2-1,y2)=(0,0).

由(1)及题设得x3=3-(x1+x2)=1,y3=-(y1+y2)=-2m<0.

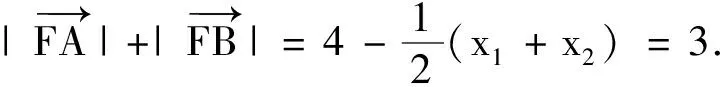
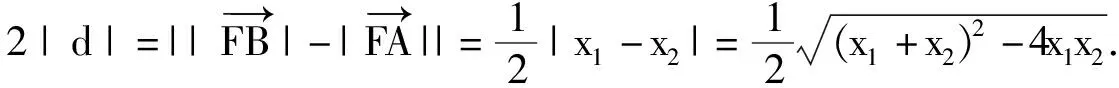
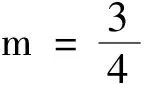
3 研究结论与教学建议

3.1 研究结论

近十年高考数学全国卷平面向量试题近九成是选择题和填空题，且选择题居多，超七成试卷只有1道平面向量试题，分值5分，超两成试卷有2道平面向量试题，分值为10分与17分(二者数量相差不大)，题目难度以易、中为主，占比和超八成，以知识融合题为主的难题占比低于两成.平面向量试题考查知识点按比例由高至低依次为数量积及模与夹角、线性运算及其几何意义、垂直、平行、平面向量基本定理，且对坐标运算的考查多于非坐标运算的考查.平面向量与其他知识的融合主要集中在圆锥曲线、三角函数与解三角形、函数、数列等.

3.2 教学建议

3.2.1理解概念，牢记公式，稳固双基

教材对于平面向量内容多是按照基本概念→线性运算及其几何意义→平面向量基本定理→坐标运算→平面向量数量积的顺序编排[3][4]，基本概念是后续知识展开的基础，特别是平面向量基本定理，是坐标运算的“根”，坐标运算是其“果”.这部分知识前面概念多，后面公式多，但就全国卷而言考查内容简单，多为选择题和填空题，考查内容基本为数量积及模与夹角、线性运算及其几何意义、垂直、平行、平面向量基本定理的简单应用，有坐标运算，也有非坐标运算.因此在教学中须让学生切实理解概念，记牢公式，稳固双基.

3.2.2画好图形，精准运算，数形结合

平面向量兼具几何与代数双重属性，教材安排也是先“几何”后“代数”的顺序，并且线性运算以及数量积运算都有丰富的物理背景，是学科交叉的良好案例.对于高中生而言，平面向量也是数形结合的良好案例.因此，在日常教学中，教师要注重学生画图习惯的养成，画对图，画好图，为之后的数学运算当好“眼睛”，在此过程中亦能培养数学抽象、直观想象、逻辑推理及数学运算素养.

3.2.3总结反思，建构体系，提升素养

在平面向量与其他知识的融合中，可以发现平面向量充当辅助工具的作用，且这类题目往往对平面向量知识的考查多在坐标运算上，也很简单，重点在于与其他知识融汇贯通，这就需要建构知识体系.高中数学知识点多，抽象程度也较高，但是好在知识之间彼此是相通的，所以我们的学习不会因所学知识的增多而负担增重，反而会因发现、理解先后知识的联系而叹为观止.因此，在教学中要注重引导学生对知识的梳理、总结、反思，总结的次数多了，学生就会发现知识间的联系，找到联系、及时反思，就能自主建构属于自己的“知识体系”，当然在此过程中也可提升数学核心素养.