基于归零神经动力学的水下无线传感器网络节点测距定位方法

杜秀娟，王丽娟，刘静萍，金龙

（1.青海师范大学计算机学院，青海 西宁 810008；2.青海省物联网重点实验室，青海 西宁 810008；3.藏语智能信息处理及应用国家重点实验室，青海 西宁 810008；4.高原科学与可持续发展研究院，青海 西宁 810008；5.兰州大学信息科学与工程学院，甘肃 兰州 730000；6.青海师范大学网络信息中心，青海 西宁 810016）

0 引言

水下无线传感器网络（UWSN,underwater wireless sensor network）逐渐成为一种实现海洋大规模监测的技术方向[1]。对于海洋资源开发和海洋灾害预警来说，能够提供精准的时空数据是对UWSN 的一个重要需求[2]。此外，还有许多UWSN 技术，如媒体访问控制（MAC,medium access control）机制、路由转发以及拓扑控制等，都依赖于节点位置信息来实现[3]。然而，水下环境的动态性或节点的自主运动导致节点位置时刻在改变，使UWSN 中的节点定位问题成为时变定位问题。如何对时变定位问题进行建模并实现快速且精确的求解值得关注。

国内外学者针对UWSN 节点定位开展了各种研究，并以测距定位方法和无测距定位方法为主[4]。前者通过测距技术获得节点间距离，进而采用三角定位法或三边定位法实现定位；后者通过节点连通性实现定位[5]。在测距定位方法中，使用的测量技术有到达角度（AoA,angle of arrival）、到达时间（ToA,time of arrival）、到达时间差（TDoA,time difference of arrival）以及接收信号强度（RSS,received signal strength）[6]。少部分位置信息已知的节点被称为锚节点；其他节点被称为未知节点，需要借助锚节点坐标来确定位置。文献[7]提出了一种被动式水下定位方案（UPS,underwater positioning scheme），未知节点通过被动接收锚节点依次发来的定位信息，采用TDoA 测量实现静默定位。文献[8]提出一种按需异步定位（ODAL,on-demand asynchronous localization）机制，将主动定位与被动定位相结合，按需实现高精度或相对低精度的定位，被动定位过程涉及TDoA 测量。借助深度传感器，文献[9]提出了一种将三维ToA 测距结果投影到二维平面的解决思路，不仅不影响定位性，还在一定程度上降低了定位难度。文献[10-11]结合ToA 和AoA信息，通过单个锚节点对水下潜器进行定位。测距定位方法的定位精度高于无测距定位方法。但上述文献都以一种静态的方式处理定位问题，并未考虑真实情况下定位问题的时变特性。鉴于此，本文使用测距定位方法，即AoA 定位算法和TDoA 定位算法，结合UWSN 节点定位问题的时变性，采用一种高效的解决办法——神经动力学方法，实现对未知节点的快速精确定位。

递归神经网络（RNN,recurrent neural network）可用于解决一些复杂问题，如时变希尔维斯特方程求解[12]、非线性优化[13]、自动控制[14]等。此外，一些基于递归神经网络的方法被用于解决无线定位问题。文献[12]提出了一种用于求解时变广义希尔维斯特方程的具有噪声抑制功能的RNN 模型，其在声源定位上的应用证明该RNN 模型适用于移动节点定位场景。此外，Assaf 等[15]针对无线信道开发了一种新的无测距定位算法用于对抗各向异性衰减。文献[16]提出的一种RNN方法被有效应用于WSN的无测距定位场景中。作为一种特殊的递归神经网络，归零神经网络及其不同程度的改进版本[17-20]为神经网络的发展和应用做出了突出贡献。归零神经动力学（ZND,zeroing neural dynamics）由神经网络发展而来，是一种特殊的神经动力学，可以保证误差函数收敛于零。如前文所述，RNN 已被应用于无线定位系统，但其与UWSN 节点定位相融合的有关工作并未被开展。本文设计了带有非线性激活函数的归零神经动力学（NL-ZND,nonlinear function-activated ZND）模型分别求解基于AoA 和TDoA 的UWSN 时变定位问题。理论分析和计算机仿真结果表明，该神经动力学模型具有良好的收敛性能、高精确度以及动态环境下的稳健性。本文主要贡献如下。

1) 将神经动力学技术拓展到UWSN 领域，使用归零神经动力学模型实现对节点定位问题的高效求解。

2) 由于水下环境的动态性或节点的自主运动，UWSN 节点定位问题为时变问题，对该问题进行分析，将其建模为线性动态矩阵方程。

3) 提出了带有非线性激活函数的改进神经动力学模型，并通过严格的数学分析证明其具有有限时间收敛性能。仿真实验表明，所提NL-ZND 模型在求解基于AoA 和TDoA 定位问题时具有较高定位精度以及移动定位稳健性。

1 定位问题及归零神经动力学方法

本节阐述了基于AoA 和TDoA 的UWSN 定位问题，并给出了这2 个问题的统一数学模型；然后，给出利用传统ZND 求解定位问题的解决方案。

1.1 定位问题

本文分别考虑了二维AoA 定位算法以及三维TDoA 定位算法。以一个小型的局部拓扑为研究范围，一个未知节点通过几个锚节点的辅助实现定位。需要说明的是，UWSN 通常被视为处于三维场景中，但对于处在相同深度的节点，可以暂时忽略深度信息，视为二维平面进行简化处理，因此本文讨论了二维AoA 定位算法。无论是二维还是三维UWSN拓扑结构，本文所提模型均具有灵活的适用性。

1.1.1 AoA 定位算法

对于AoA 定位算法，未知节点的位置坐标需借助通信信号（声波信号）在接收节点即锚节点处的到达角度求得。考虑在一个二维场景中，未知节点的位置随时间而改变，锚节点则被随机部署，且位置固定。首先，定义m个锚节点的坐标H以及未知节点的坐标h(t)分别为

根据AoA 的几何意义，在任一时刻，每个锚节点与未知节点的AoA 的正切函数值为

其中，i∈ ｛1,2,…,m｝，αi(t)表示未知节点与第i个锚节点的通信信号到达角度。式(1)可被等价转化为-tan(αi(t))x(t)+y(t)=yi-xitan(αi(t))。最终，二维场景下基于AoA 的节点定位问题可表示为

1.1.2 TDoA 定位算法

TDoA 定位算法通过测量未知节点发出的通信信号分别到达各个锚节点的时间差来估计未知节点的位置，其考虑的是一个动态的三维场景。定义m个锚节点的坐标N和未知节点的坐标n(t)分别为

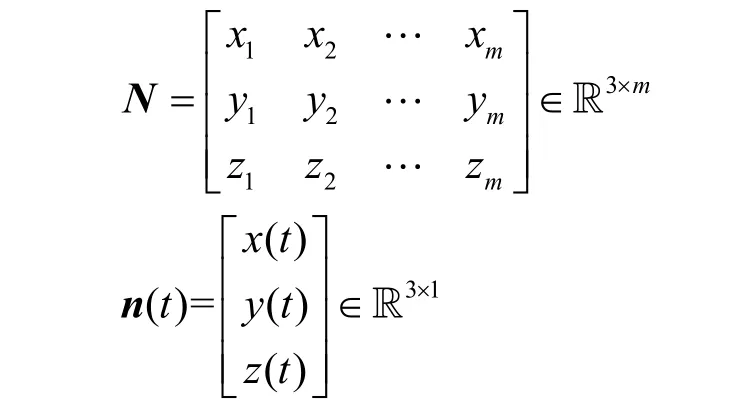
根据TDoA 的物理意义可得

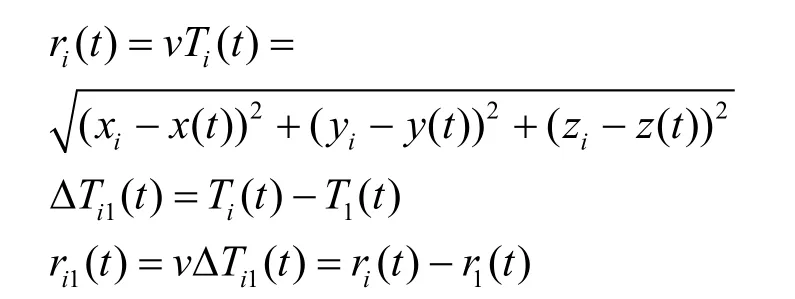
其中，i∈ ｛1,2,…,m｝，v表示通信信号在介质中的传播速度，Ti(t)表示信号从未知节点到第i个锚节点的传播时间，ΔTi1(t)表示信号从未知节点分别传播到第i个和第一个锚节点的时间差，ri(t)表示未知节点和第i个锚节点间的距离，ri1(t)表示未知节点到第i个和第一个锚节点的距离差。经推导（如附录1 所示）可得三维场景中基于TDoA 的节点定位问题为

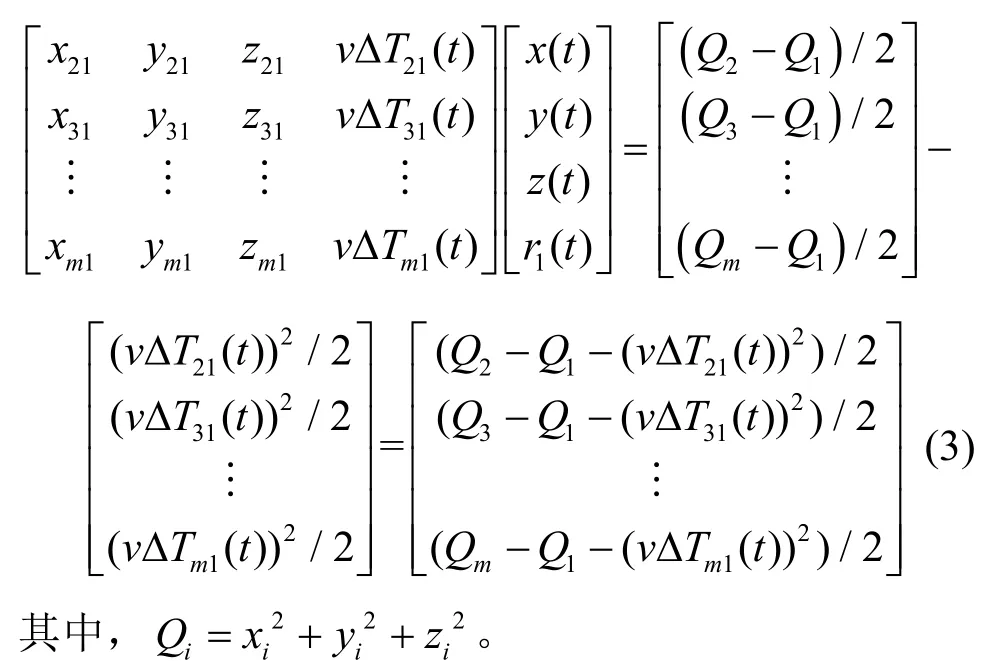
1.1.3 统一的表达式

根据式(2)和式(3)，基于AoA和TDoA的UWSN定位问题可表示为动态矩阵方程，即

其中，P(t) ∈Rp×q为已知的系数矩阵，并且涉及通信信号的到达角度和到达时间差；z(t) ∈Rp为已知向量；s(t) ∈Rq（q=2或者q=4）为未知向量，并且涉及未知节点的待求位置。

1.2 传统ZND 模型

目前，ZND 在动态问题上已得到了较好的应用。传统ZND 模型的构建分为以下3 个步骤。

步骤1构建误差函数e(t)=P(t)s(t) -z(t) ∈Rp。

步骤2为了保证误差函数e(t)的每一个元素收敛于0，定义演化方程e˙ (t)=-γF(e(t))，其中，e˙ (t)为e(t)的时间导数；缩放因子γ＞ 0；F(·) : Rp→Rp为线性激活函数组，其中的每个元素为f(·):R →R。

步骤3将e(t)误差函数代入演化方程，获得用于求解UWSN 定位问题式(4)的传统归零神经动力学求解方案，即

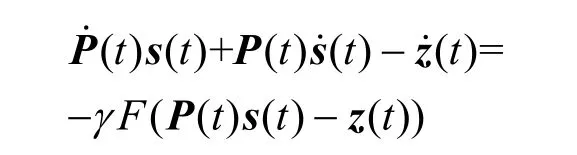
2 改进的归零神经动力学模型

基于以上ZND 模型，本文进一步探索并提出了一种改进的归零神经动力学模型——NL-ZND 模型，用来求解式(4)。

2.1 NL-ZND 模型

首先，定义误差函数为e(t)=P(t)s(t) -z(t)∈Rp；然后，采用非线性的单调递增的奇函数加快e(t)收敛。因此，步骤2 中的演化方程可改写为

其中，φ为一个正值，用于控制神经动力学模型的收敛速率；与传统ZND 模型所使用的线性激活函数组F(·): Rp→Rp不同，L(·) :Rp→Rp为一组单调递增的奇函数ι(·) : R →R，使误差函数的每一项都在有限时间内收敛于零。式(5)中，等号左边表示e(t)的变化率，右边表示以负反馈的方式使e(t)趋近于0。对于实际应用中的网络部署场景，式(4)在数学上通常是正定或超定的。接下来，利用式(5)得出正定情况下求解UWSN 定位问题的神经动力学模型为

其中，P+(t)表示矩阵P(t)的逆矩阵。对于超定情况（p＞q），通过将误差函数代入式(5)并对两边同时乘以P(t)T，得到神经动力学模型为

如果P(t)是列满秩的，那么P+(t)P(t)是可逆的，并且P+(t)=(P(t)TP(t))-1P(t)T成立。因此，式(7)可写作

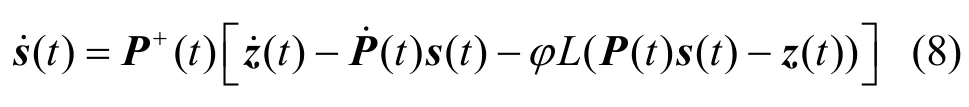
显然，正定或者超定情况下的神经动力学模型是一致的。因此，用于求解UWSN 定位问题的神经动力学模型可以统一表示为式(8)。从上述分析中可以看出，式(7)和式(8)在一定情况下是等价的，本文在后续的计算机仿真实验中也证实了这一点。仿真部分展示的式(8)模型的结果同样可以解释式(7)模型。

一般而言，一个激活函数表示从一个集合到另一个集合的投影操作，不同的激活函数产生不同的收敛性能。使用线性激活函数的ZND 模型往往花费较长时间达到收敛效果。因此，本文基于式(8)模型，提出了带有非激活函数的归零神经动力学模型来求解UWSN 定位问题式(4)，并对其收敛性能进行了严格的理论证明。

正如前文所述，使用线性激活函数的ZND 模型的能力是受限的。受文献[21]的启发，本文将一个特殊设计的非线性激活函数应用于式(8)模型，即

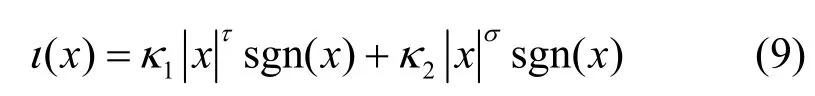
其中，符号| |表示标量的绝对值；缩放因子κ1,κ2＞ 0；设计参数τ∈ (0,1)，σ∈ [1,+∞)。符号函数定义如下

将激活函数式(9)代入式(8)，可以得到用于求解定位问题式(4)的改进神经动力学模型为

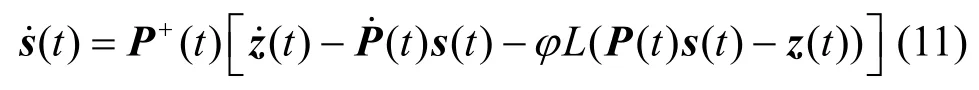
式(11)所示改进模型称为NL-ZND 模型。接下来，本文对NL-ZND 模型的收敛性能进行理论证明。

2.2 收敛性分析

定理1给定一个任意的初始位置s(0)，由NLZND模型估计的未知节点运动的实时位置可以在有限时间C内收敛于理论位置s*(t)，有限时间C表示为

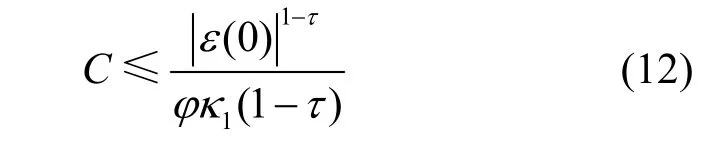
其中，ε(0)为误差e(0)中绝对值最大的元素。

证明s*(t)是基于AoA 或基于TDoA 的UWSN 定位问题的理论解。从一个随机产生的初始值s(0)开始，由NL-ZND 模型生成的状态向量s(t)将在有限时间C内收敛于s*(t)。根据误差函数的定义，当误差函数收敛于0 时，s(t)收敛于s*(t)。因此，可以对误差函数e(t)进行讨论。针对第i个子系统可以定义为

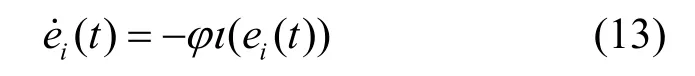
然后，定义ε(t)为向量e(t)中绝对值最大的元素，即在t时刻，对于所有的i(i=1,2,…,p)都有成立。根据ε(0)的符号，分为以下3 种情况进行讨论。

情况1意味着当ε(t)达到0 时，ei(t)收敛于0。设C为ε(t)的收敛时间，也就是NL-ZND 模型在时间C收敛于理论解。基于ι(x)的定义，可通过式(14)～式(18)来计算C。

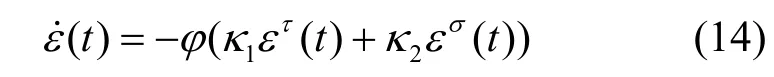
因为κ2εσ(t)＞0，式(14)可化简为

根据微分的概念，可写为如下形式

两边同时积分可得

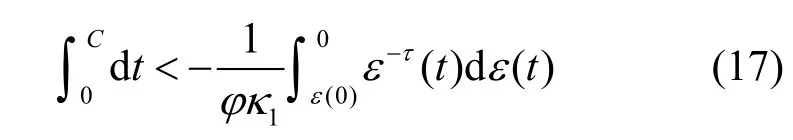
求解式(17)可得

情况2ε(0) ＜ 0。经过与情况1 类似的推导，可得收敛时间为

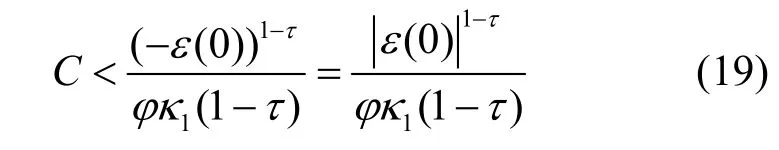
情况3ε(0)=0。经过与情况1 类似的推导，可得收敛时间为

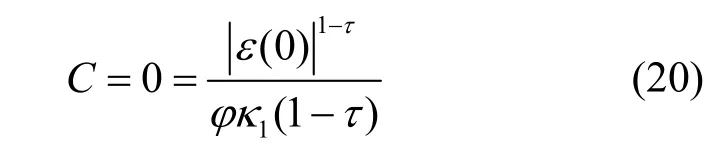
从上述3 种情况的分析可得，NL-ZND 模型在求解式(4)时将在有限时间C内收敛于理论解，也就是说，未知节点的位置在时间C内收敛于理论位置。

需要说明的是，从时变的角度出发，将节点定位问题建模为控制理论中的调节问题，即P(t)s(t)=z(t)，进而得到该问题的误差函数为e(t)=P(t)s(t) -z(t)。NL-ZND 模型的目的是使误差函数e(t)收敛到0，即可得出未知节点的位置s(t)。NL-ZND 模型被设计为一个常微分方程形式的动力学系统，当其达到收敛状态时，该模型的平衡点与定位问题的解s(t)相同。

2.3 复杂度对比

本节分别给出了NL-ZND 模型和传统ZND 模型的计算复杂度。

从离散的角度计算本文所提出的神经动力学模型的复杂度。首先，利用欧拉差分公式对式(11)进行离散化可得

其中，τ＞ 0∈R 为采样间隔，k=1,2,…为迭代索引，

()L· 为激活函数，。模型在第k个时刻产生的运算包括对Γk和sk+1的求解。此外，本文定义浮点运算如下。

1) 一个标量和一个向量（大小为ζ1）相乘需进行ζ1次浮点运算。

2) 一个矩阵（大小为ζ1×ζ2）和一个向量（大小为ζ2）相乘需进行ζ1(2ζ2-1)次浮点运算。

3) 2 个向量（大小都为ζ1）相加或相减需进行ζ1次浮点运算。

4) 一个方阵（大小为ζ1×ζ1）求逆需进行ζ13次浮点运算。

本文以正定情况下的复杂度为参考（即p=q）。在第k个时刻，计算Γk需要q3+6q2+(τ+σ+5)q次浮点运算，计算sk+1需要 2q次运算。因此，本文所提神经动力学模型在每个采样间隔需进行q3+6q2+(τ+σ+7)q次浮点运算。不同于陆地的传感器节点，水下的节点具备了更高的计算能力，可以满足处理上述规模的计算以实现定位需求。

本文以相同的方式得出传统ZND 模型在每个采样间隔需进行q3+6q2+3q次浮点运算。由于采用了非线性激活函数，本文所提NL-ZND 模型的复杂度比传统ZND 模型高，并且在每个采样间隔增加了τ+σ+4q次运算，其中，τ∈ (0,1)，σ＞ 1，q=2或4。增加的运算次数τ+σ+4q只是q的一阶函数，但模型的收敛速度却得到很大提升。

3 仿真实验

本文首先进行了基于AoA 和TDoA 的定位仿真实验，实验结果验证了NL-ZND 模型在求解UWSN 定位问题时的有效性；然后，对NL-ZND 模型在收敛时间和收敛速率等方面的性能进行仿真验证；最后，将该模型应用在UWSN 实验床中的节点定位以进一步说明模型的可行性。

3.1 基于AoA 的UWSN 节点定位

本节模拟了一个 30 m×20 m 范围的二维UWSN 场景，其中，未知节点沿“钻石形”轨迹运动，周围的4 个锚节点被随机部署且位置固定，如图1(a)所示。从图1(a)可以看出，未知节点的真实轨迹与模拟轨迹几乎是重合的。图1(b)展示了剩余误差的收敛情况。图1(c)描述了位置估计误差，X坐标估计误差epX和Y坐标估计误差epY均在短时间内收敛到足够小，达到10-4级别。因此，本文所提神经动力学模型具有较高的定位精度。

图1 基于AoA 的UWSN 节点定位仿真实验

综上所述，所提神经动力学模型在求解基于AoA的节点定位问题时，可以正确计算出节点的运动轨迹，并且具有较高的精确度以及快速的收敛性能。

3.2 基于TDoA 的UWSN 节点定位

本节进行了基于TDoA 的UWSN 节点定位仿真实验，实验结果如图2 所示。

图2 基于TDoA 的UWSN 节点定位仿真实验

如图2(a)所示，锚节点被随机且固定地部署在1.4 km×1.4 km×30 m 的三维空间内，未知节点在空间内沿Z轴正方向做螺旋线运动。NL-ZND 模型针对未知节点生成的模拟轨迹与真实轨迹重合。如图2(b)所示，模型生成的剩余误差在1 s 内收敛。如图 2(c)所示，模型收敛时，位置估计误差epX、epY、epZ的阶数均为10-3。验证了所提模型解决基于TDoA 的UWSN 节点定位问题的有效性。

综上所述，所提神经动力学模型在求解基于TDoA 的节点定位问题时，可以正确计算出节点的运动轨迹，并且具有较高的精确度以及快速的收敛性能。

3.3 对比验证

本节分别对NL-ZND 模型进行了收敛时间、收敛速率方面的性能验证，此外，还观察了锚节点数量及分布情况对定位结果的影响。

3.3.1 收敛时间

借助3.1 节中基于AoA 定位和3.2 节中基于TDoA 定位的实验场景，本节对NL-ZND 模型和传统ZND 模型的收敛时间进行了对比，结果如图3 所示。

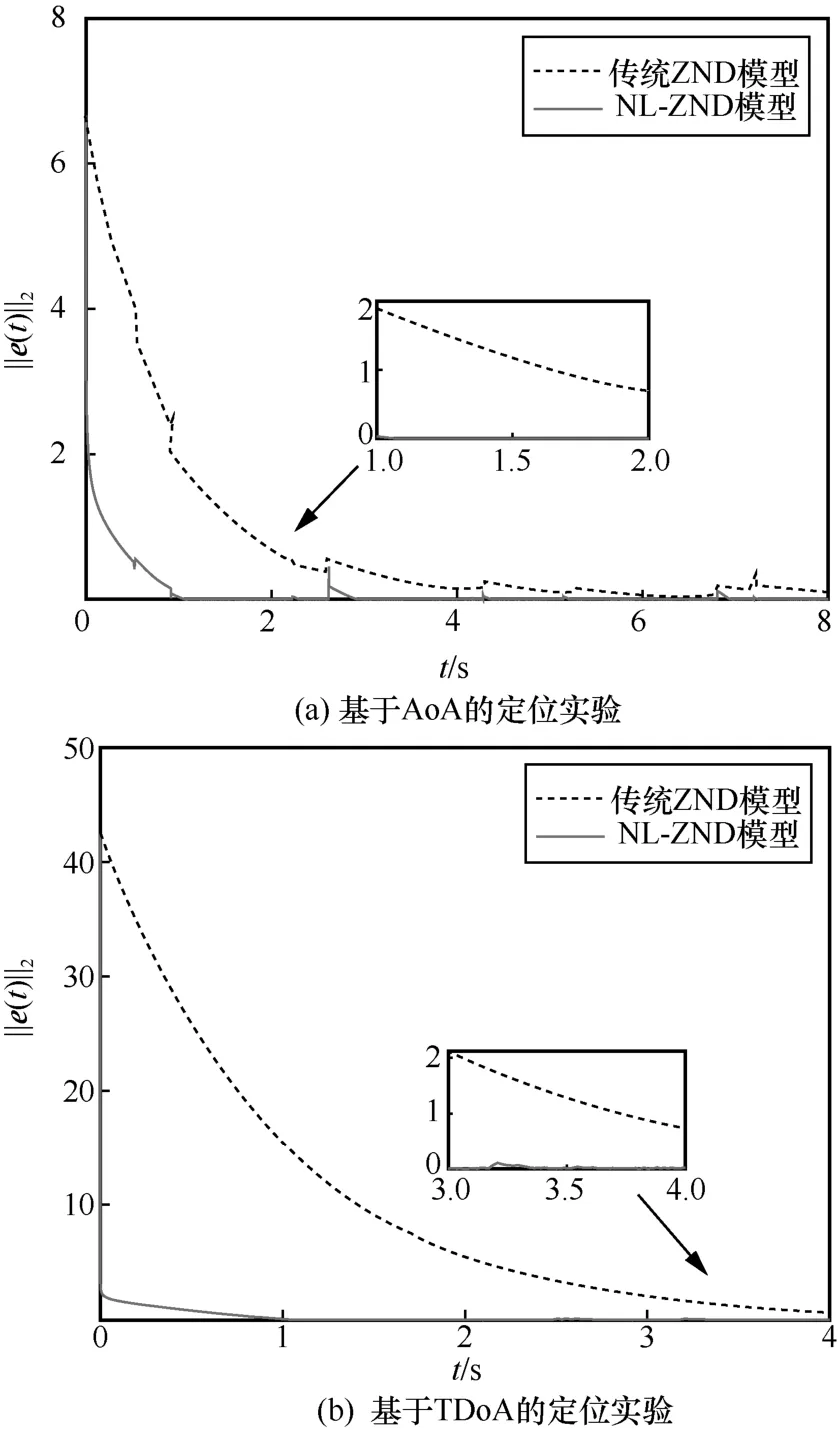
图3 收敛时间对比

从图3(a)可以看出，使用NL-ZND模型和传统ZND模型求解基于AoA 的定位问题时，NL-ZND 模型的剩余误差在2 s 内收敛到0，而此时传统ZND 模型还存在较大误差且并未达到收敛状态。从图3(b)可以看出，求解基于TDoA 的定位问题时，NL-ZND 模型在1 s 时收敛，而传统ZND 模型在仿真结束时仍未达到收敛状态并且存在较大误差。以上仿真结果有效地验证了本文提出的NL-ZND 模型具有有限时间收敛性能。

3.3.2 收敛速率

在NL-ZND 模型中，φ是一个正值，用于控制神经动力学模型的收敛速率。本节借助3.2 节的实验场景，设置φ分别为0.5、1、2，对NL-ZND模型的收敛速率进行了仿真验证，结果如图4 所示。从图4 可以看出，随着φ的增大，曲线斜率逐渐变大，即收敛速率逐渐增大；相应地，收敛时间缩短，从而验证了NL-ZND 模型中φ具有调节收敛速率的作用。

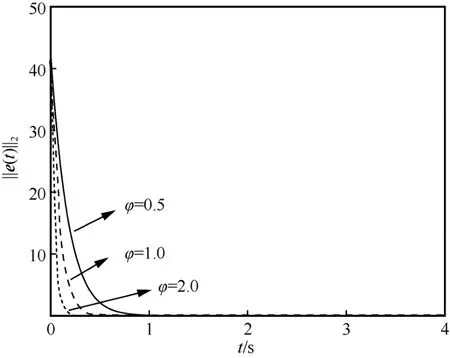
图4 NL-ZND 模型收敛速率验证

3.3.3 锚节点数量及分布

为了观察锚节点数量对定位结果的影响，本节将锚节点的数量设置为4～8 个，并在二维TDoA 定位场景中进行多次仿真实验，得到相应的定位误差

。未知节点运动轨迹及锚节点A1～A8分布如图5 所示，锚节点数量及定位误差如表1 所示。

图5 未知节点运动轨迹及锚节点分布

表1 锚节点数量及定位误差

如表1 所示，随着锚节点数量的增加，未知节点的定位误差降低。当锚节点数量达到TDoA 定位所需的最小节点数4 个时，本文所提NL-ZND 模型的定位结果即可满足大多数应用的精度需求。然而考虑到实际部署场景，锚节点数量不会过于密集。随着锚节点数量的增多，网络中会不可避免地产生信号碰撞等问题，从而影响定位效果。

3.4 在UWSN 实验床的应用

本文团队已成功搭建了一个集成Micro-ANP协议栈[22-24]的UWSN 实验床，并在青海湖进行了大量的湖试实验。实验床主要由工业路由器、节点和远程服务器构成。每套节点又包括一个C15 CTD 传感器、一个AquaSeNT OFDM modem 和一个树莓派开发板。本节利用实验床中部署的节点的地理坐标进行基于AoA 的定位实验。在本节实验中，节点的深度是忽略不计的，并且不考虑湖水流动速度。

基于AoA 的节点定位实验结果如图6 所示。实验拓扑如图6(a)所示，节点A1～A4是配备了GPS 模块的锚节点。未知节点U1的实际坐标为(36.706 770,100.544 254)。位置估计误差的收敛情况如图6(b)所示。从图6 可以看出，未知节点U1的实际位置被正确地计算出来。因此，NL-ZND模型在求解UWSN 实验床中基于AoA 的节点定位问题时具有潜在的适用性。

图6 基于AoA 的节点定位实验结果

4 结束语

本文对神经动力学方法进行了探讨并将其拓展到UWSN 领域。针对UWSN 定位问题，提出了改进的神经动力学模型，并对模型的收敛性能进行了严格的理论分析。在仿真部分，该模型成功地应用于基于AoA 和TDoA 的UWSN 节点定位问题，证明了模型在高精度和动态环境稳健性方面的有效性。此外，实验验证了所提模型具备有限时间收敛性能。目前，大多数UWSN 协议及算法的测试都基于仿真软件，本文通过对UWSN 实验床中的节点进行定位实验，说明了神经动力学模型在真实环境中的潜在适用性。

附录1 三维场景中基于TDoA 的节点定位问题推导过程