Málaga 湍流信道下改进型光广义空间调制

赵辉，马薇雯，李进，邓文超，万辉，张天骐，刘媛妮

（1.重庆邮电大学通信与信息工程学院，重庆 400065；2.信号与信息处理重庆市重点实验室，重庆 400065；3.重庆邮电大学网络空间安全与信息法学院，重庆 400065）

0 引言

近年来，自由空间光通信（FSOC,free space optical communication）[1-2]凭借安全性高、传输带宽大、抗干扰能力强、实施成本低等诸多优势引起人们广泛关注。然而，大气湍流和指向误差[3-4]一直制约着其发展。光空间调制（OSM,optical spatial modulation）作为一种新型的光多输入多输出技术，由于每个符号周期仅激活一根光学天线，不仅有效避免了传统多输入多输出技术[5]信道间干扰强和天线间同步难等问题，还降低了链路成本和接收端信号检测复杂度。此外，OSM 不仅采用传统数字调制星座（即信号域）传递信息，还通过天线索引（即空间域）来承载信息，很大程度上提高了系统的频谱效率。因此，近年来OSM 引起了学者的广泛关注，高效的OSM 方案是FSOC 系统抵抗大气湍流和指向误差效应、提升系统性能的有效保障。

2015 年，Ozbilgin 等[6]将OSM 与脉冲位置调制和脉冲幅度调制相结合，构建了一种适用于大气激光通信的空间调制方案，并给出了该方案在对数正态和Gamma-Gamma 信道下的理论分析框架。2017 年，Jaiswal 等[7]提出了光空移键控（OSSK,optical space shift keying）调制方案，并推导了系统在Gamma-Gamma 信道上的平均误码率上界。该方案只利用空间域传输信息，相较于OSM 收发器设计更加简单。2020 年，王惠琴等[8]提出了光完全广义空间调制方案，通过激活不同数量的光学天线使系统的频谱效率随光学天线数量的增加呈线性增长，并分析了该方案在对数正态信道下的误码率性能。2021 年，Bhowal 等[9]研究了带有指向误差的Gamma-Gamma 信道下的光广义空间调制（OGSM,optical generalized spatial modulation），通过光学天线组合的方式增加可选激活状态，克服了OSM 光学天线数量必须为2 的整数次幂的限制，提高了系统的频谱效率。

目前，FSOC 光空间调制技术的研究刚刚起步，现有研究大多致力于如何提高系统的频谱效率，且已有方案只针对Gamma-Gamma信道或对数正态信道展开研究，不能全面反映所有湍流状态下的系统性能。同时，现有方案大多选取预先固定的光学天线或天线组合，不仅浪费空间资源，而且由于没有考虑时变的信道状态信息（CSI,channel state information）限制了系统的误码率性能。因此，本文结合CSI，提出一种基于欧氏距离的低复杂度发射天线组合集自适应选择算法。与经典的欧氏距离最优天线选择（EDAS,Euclidean distance optimized antenna selection）算法[10]相比，本文所提算法在牺牲较小误码率性能的条件下较大程度降低了光学天线组合集选择的复杂度。此外，为了反映真实湍流信道下的系统性能，本文采用可以表征所有大气湍流状态的Málaga 湍流[11-13]信道，综合考虑大气湍流、指向误差和路径损耗的联合影响，分析系统误码率性能，并推导出OGSM 方案的误码率上界。

1 信道与系统模型

1.1 信道模型

采用适用于所有湍流强度的Málaga 湍流信道，同时考虑指向误差和路径损耗的影响，信道衰减系数可以建模为[14]

其中，ha为大气湍流引起的信道增益；hl为路径损耗，当传输距离一定时hl可被认为是固定的；hp为指向误差，其概率密度函数（PDF,probability density function）可以表示为[4]

其中，g=2bo（1 -ρo）为离轴涡旋接收到的散射分量的平均功率；2bo为总散射分量的平均功率；为散射分量和非散射分量产生的相干光平均功率，Ω为视距分量的光信号平均功率，φA和φB分别为视距分量和耦合到视距分量的散射分量的相位，ρo为耦合到视距分量的散射功率量（0 ≤ρo≤ 1），α为与散射过程中大尺度涡旋的有效个数相关的正参数，β为衰落参数且为自然数，G［·］ 为Meijer G 函数[15]。

1.2 系统模型

改进型OGSM 系统模型如图1 所示。设系统含有Nt根光学天线（OA,optical antenna）和Nr个光电探测器（PD,photoelectric detector），发送端每次激活Na根光学天线，采用M阶的QAM。系统的频谱效率为

图1 改进型OGSM 系统模型

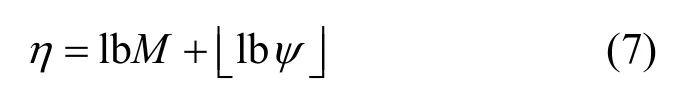
具体地，在每个传输周期内，二进制比特流输入系统后经过串并变换被分为两部分。其中，前lbM个比特映射为M阶的 QAM 符号，后个比特映射为特定的光学天线组合来发射调制符号。

一个大气信道是一个时变信道，光信号经过不同的子信道时会受到不同程度的衰落影响。因此，接收端根据当前CSI，结合天线组合集选择算法动态地从ψ种光学天线组合中选出个光学天线组合，作为当前状态下的最佳光学天线组合集，并通过反馈链路反馈给发射端。发射端根据空间域比特映射的天线组合序号激活对应的Na根光学天线来发送调制符号。因此，系统发送的传输信号为

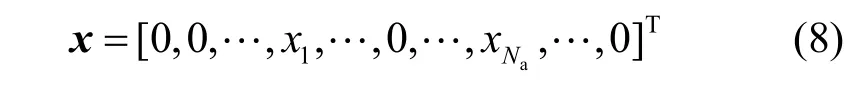
其中，x为 1×Nt维的向量；为发送的Na个调制符号，其位置对应激活光学天线的索引号。

电信号经过直流偏置转换为光信号，经过大气信道传播后，光电探测器接收到的信号为

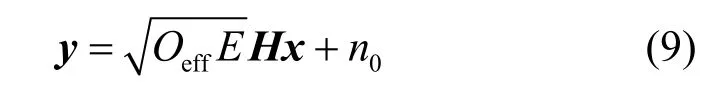
其中，Oeff是系统的光学效率，E是平均符号能量，H是Nr×Nt的信道矩阵，是均值为0、方差为的加性白高斯噪声。

接收端采用最大似然（ML,maximum likelihood）算法从受到信道衰落和噪声干扰的接收信号y中估计原始发送信号。其基本原理为

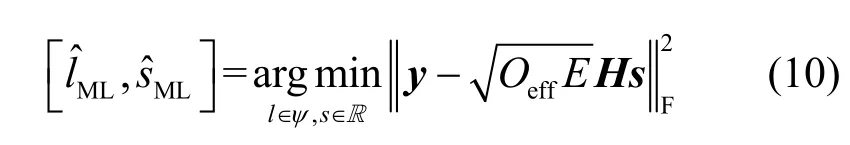
可见，改进型OGSM 系统充分考虑动态的信道状态信息，自适应选择最佳发射天线组合集，在提高系统空间资源利用率的同时，通过有效利用最优信道改善系统的误码率性能。

2 低复杂度发射天线组合集选择算法

经典的天线选择算法包括EDAS 算法、基于天线相关性（AC,antenna correlation）准则[16]和最大化信道范数的天线选择算法[8]等。对于采用ML 检测的光空间调制系统，接收机的性能与传输向量之间的最小欧氏距离有关。因此，EDAS算法性能最优，但需要遍历所有可能的候选天线组合和所有可能的接收星座点，复杂度高。为此，本文基于欧氏距离等价原则，提出一种低复杂度光学天线组合集选择算法，简称 LCED（low complexity Euclidean distance）算法，以改善OGSM 方案的误码率性能。

在OSM 系统中，光学天线之间的欧氏距离可以表示为

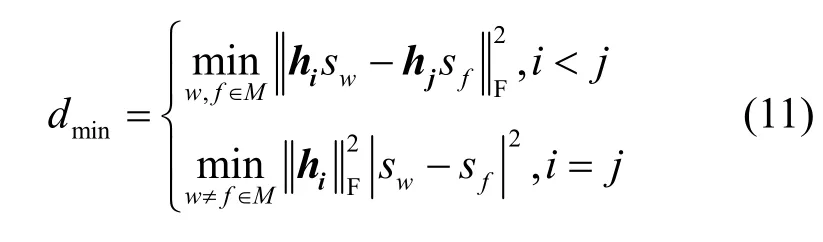
其中，hi和hj表示信道矩阵中光学天线索引号对应的列向量，sw和sf表示发送的QAM符号。而OGSM系统需要考虑光学天线组合之间的距离。此时，表示光学天线组合对应的信道矩阵列向量的和。

由式(12)可知，i*和j*不会同时存在于最优光学天线子集中。

基于此，本文通过降低光学天线组合对应的欧氏距离矩阵维度，提出了一种低复杂度光学天线组合集选择算法，具体流程如下。

1) 根据式(11)计算上三角距离矩阵为

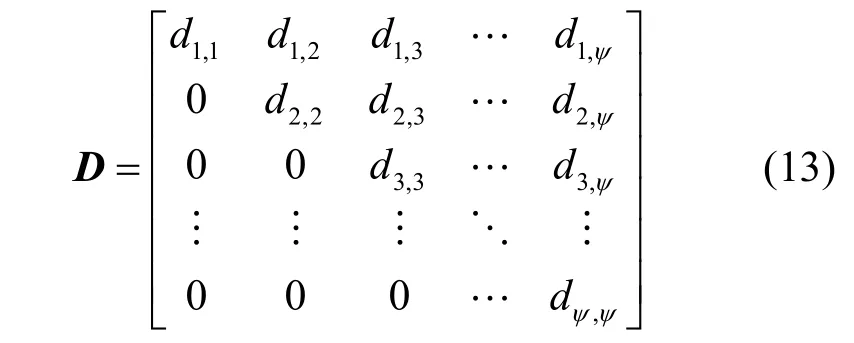
其中，矩阵元素di,j代表光学天线组合之间的欧氏距离。矩阵的大小由光学天线组合个数ψ决定。

2) 找出D中欧氏距离的最小值。根据天线组合相关对称性的特点[18]，D中元素的最小值可能不止一个。设矩阵D中元素最小值集合为

3) 确定κ的大小，需要删除的组合个数为ψ-κ。计算集合I中各元素所对应的天线组合范数，删除范数较小的光学天线组合。如果同时删除hi和hp对应的行和列以得到新的距离矩阵。若需要删除的光学天线组合个数τ（τ＜ψ-κ）小于集合I中元素的个数，则只计算I中前τ个元素所对应的范数。

4) 重复步骤2)～步骤3)，直到D的大小恰好为κ×κ。矩阵元素对应的天线组合即当前信道状态下的最佳光学天线组合集。

具体地，考虑一个含有4 根光学天线和4 个光电探测器的OGSM 系统，光学假设该系统每次激活2根光学天线，使用4-QAM，光学天线组合集选择算法示例如图 2 所示。可能的光学天线组合为Ψ=｛ψ1,ψ2,ψ3,ψ4,ψ5,ψ6｝，如图2(a)所示。根据式(11)计算出上三角距离矩阵，如图2(b)所示。可见，d1,2与d5,6、d1,3与d4,6、d1,4与d3,6、d1,5与d2,6、d2,3与d4,5、d2,4与d3,5分别相等。找到矩阵的最小值1.072 6，其分别对应ψ1与ψ2、ψ5与ψ6之间的欧氏距离。再根据计算ψ1与ψ2、ψ5与ψ6的范数，其中，Hψi表示光学天线组合对应的信道矩阵的列向量，有ψ1＜ψ2、ψ5＜ψ6，删除范数小的ψ1和ψ5对应的组合，则最后剩下的天线组合即当前信道状态下系统的最优光学天线组合集，如图2(c)所示。

图2 天线组合集选择算法示例

综上，本文所提算法不需要遍历所有可能的光学天线组合集，也不需要重复计算光学天线组合之间的欧氏距离，相比于EDAS 算法，复杂度显著降低，更加适用于实际FSOC。

3 性能分析

3.1 复杂度分析

光学天线组合集选择算法的复杂度由搜索复杂度和计算复杂度组成。对于本文所提LCED 算法，在第δ次迭代时矩阵中有个元素。若每次搜索的最小值集合都只包含一个元素，则需要次搜索找出最小值。若每次搜索的最小值集合包含多个最小值，则需要次对比操作。因此，所提LCED 算法的搜索复杂度为

类似地，可以得到EDAS 算法和ACAS 算法的搜索复杂度和计算复杂度。不同算法的复杂度对比如表1 所示。可见，EDAS 算法和LCED 算法的复杂度与Nt、Na、Nr、M有关，ACAS 算法的复杂度与Nt、Na、Nr有关。

表1 不同算法的复杂度对比

表2 和表3 分别为Na=2，Nr=4，M=4时系统所需搜索复杂度和计算复杂度与Nt的关系。由表2 可知，增加光学天线的数量，EDAS 算法、ACAS算法的搜索复杂度都会急剧增加。当Nt=4时，本文所提LCED 算法的搜索复杂度比EDAS 算法、ACAS 算法最多可降低86.6%、77.5%。从表3 可以看出，当Nt=6时，EDAS 算法、ACAS 算法分别需要74 851 920、2 702 700 次乘法运算，而LCED算法仅需42 810 次乘法运算。可见，本文所提LCED算法相比于经典的天线选择算法在复杂度方面更具优势，且随着光学天线数量的增加，这种优势更加明显。

表2 搜索复杂度与Nt 的关系

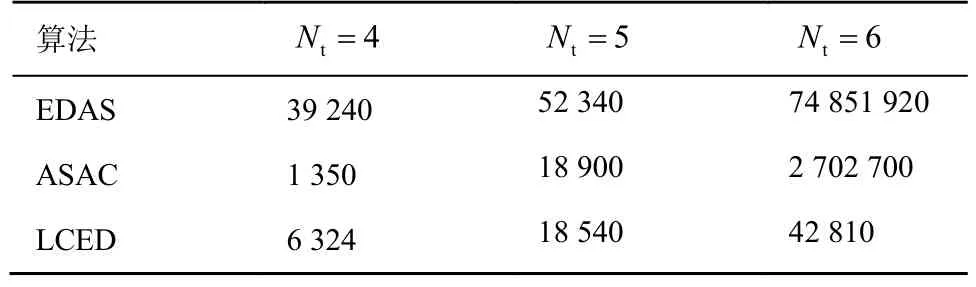
表3 计算复杂度与Nt 的关系

3.2 误码率分析

为避免传统联合上界分析法在高阶调制和少量光电探测器的情况下分析精度受限的问题[19-20]，本文在计算误码率上界时，分别考虑空间域和信号域。因此，系统的平均误码率（ABER,average bit error rate）上界可以表示为[9]

其中，Psymbol表示调制符号s被检错成s＇所引起的ABER，Pindex表示光学天线索引号j被检错成i所引起的ABER，且有

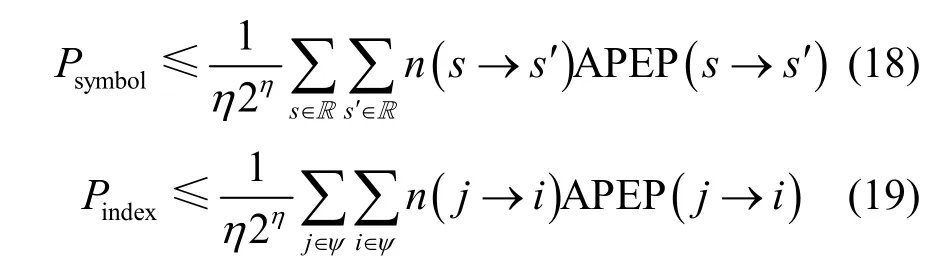
其中，n（s→s＇）和n（j→i）分别表示信号域和空间域检测错误的比特数，APEP（s→s＇）和APEP（j→i）分别表示信号域和空间域的平均成对错误率（APEP,average pairwise error probability）。

根据文献[9]，APEP（s→s＇）可以表示为

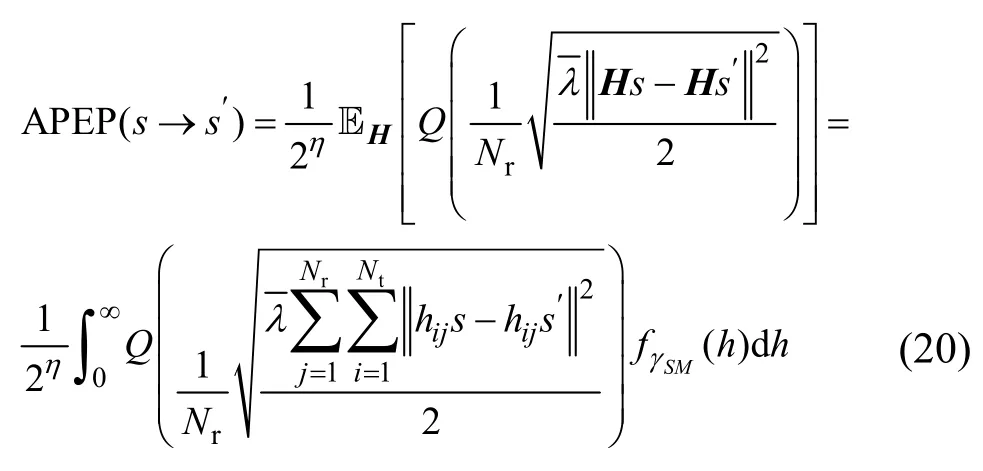
空间域的APEP 为

详细推导过程如附录1 所示。

由于式(21)包含的k为0 →∞的无穷级数和，无法精确计算，可通过将式(21) 中的无穷求和级数截断为求和变量的有限项求出近似值。下面，证明式(21)中无穷级数的收敛性。令

由于式(24)中2 个MeijerG函数的比值对于k的所有值都是非零实数，且分母中k的阶数比分子中k的阶数多1，因此，故无穷级数绝对收敛。图3 为不同SNR、ξ值和湍流强度下空间域APEP 随k值的变化。可见，随着k值的增大，APEP 趋于收敛，且SNR 越高，APEP 收敛得越快。因此，考虑不同参数对OGSM 系统的影响，在利用MATLAB 计算空间域APEP 时，令k=10，此时由级数截断引起的误差可忽略不计。

图3 空间域APEP 随k 值的变化

4 仿真分析

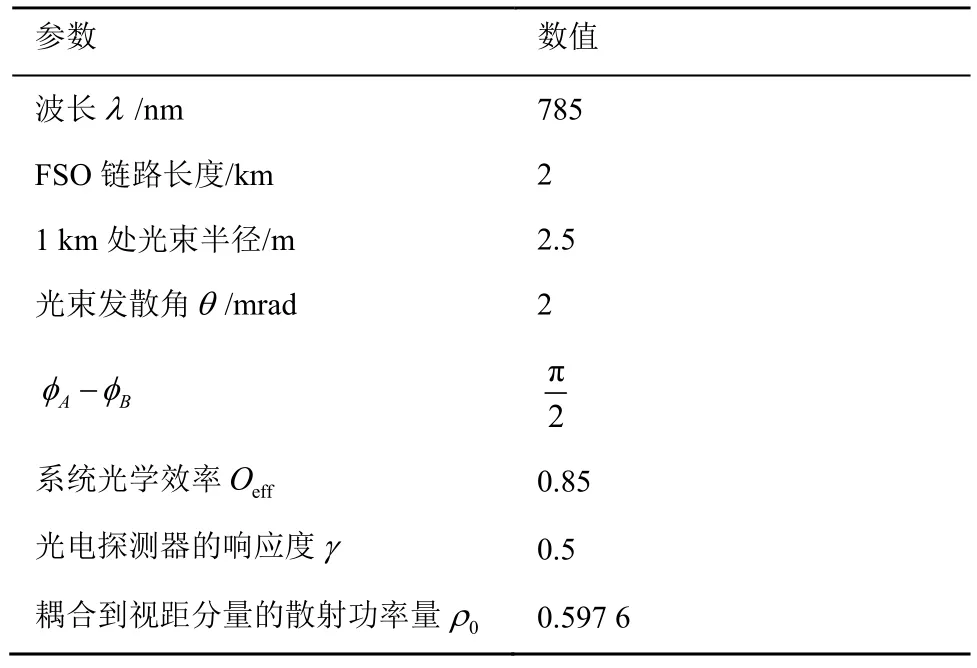
表4 系统参数

不同光电探测器数量下OGSM 系统的理论误码率与实际误码率仿真结果对比如图4 所示。仿真参数如下：ξ=1.1，强湍流，Nt=4，Na=2，M=4。由图4 可知，在低信噪比区域，OGSM 系统受噪声影响较大，导致理论误码率的计算误差较大。随着信噪比的逐渐增加，理论误码率曲线与实际误码率曲线趋于重合，验证了本文理论推导的正确性。此外，当 ABER=1 ×10-5时，相较于Nr=4，Nr=5时的信噪比增益约为4 dB；相较于Nr=5，Nr=6时的信噪比增益约为3.5 dB。由此可知，光电探测器数量的增加可以提高OGSM 系统的接收分集增益，进而改善系统的误码率性能。

图4 理论误码率与实际误码率仿真结果对比

指向误差与湍流强度对OGSM 系统误码率性能的影响如图5 所示。仿真参数如下：Nt=4，Nr=4，Na=2，M=4。由图5 可知，当ξ=1.1、ABER=1 ×10-5时，与弱湍流相比，强湍流下的信噪比损失了约4 dB。这说明当指向误差一定时，OGSM 系统的误码率性能随湍流强度的增加而逐渐恶化。此外，在弱湍流的条件下，当ξ=1.1时，系统达到 ABER=1 ×10-4所需的信噪比约为29 dB；而当ξ=0.53时，系统达到相同ABER 所需的信噪比约为40 dB，相较于ξ=1.1的情况，信噪比损失了约11dB。这说明当湍流强度一定时，指向误差越大（即ξ值越小），OGSM 系统的误码率性能越差。

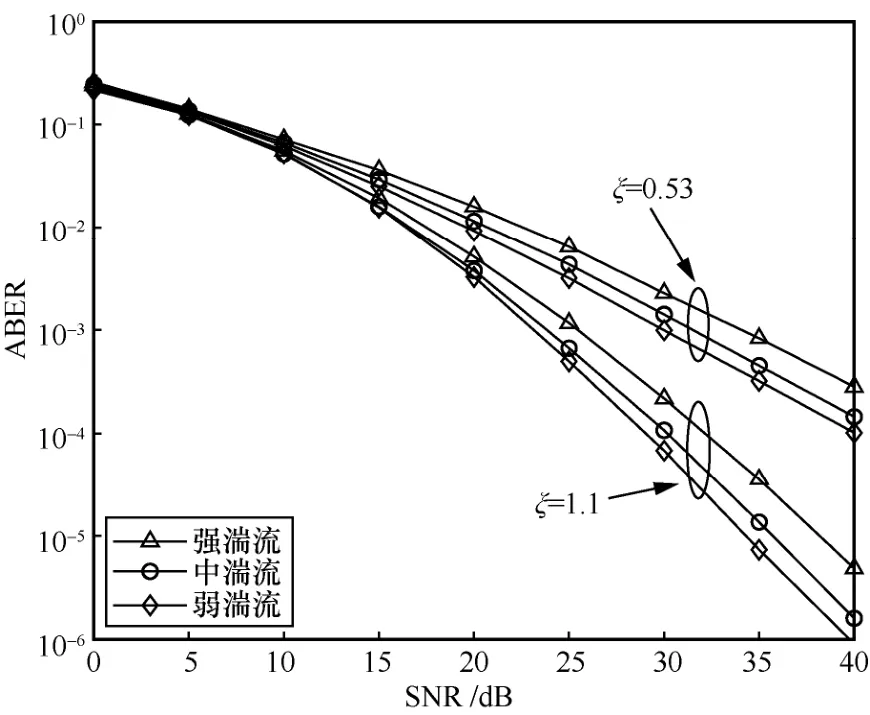
图5 指向误差与湍流强度对OGSM 系统误码率性能的影响

不同Nt和Na对OGSM 系统误码率性能的影响如图6 所示。仿真条件如下：频谱效率为5 bpcu（bpcu指每信道中传输的比特数），Nr=4，ξ=1.1，M=4，强湍流。由图 6 可知，(5-4-2)OGSM 方案与(6-4-2)OGSM 方案的误码率曲线基本重合，2 种方案所需的光学天线组合数κ相等。这说明OGSM 系统误码率性能实际上与光学天线组合数κ有关，与Nt无直接关系。但是采用LCED 算法后，OGSM 系统的误码率性能更优。例如，当 ABER=1 ×10-4、Nt为5 和6 时，本文所提LCED-OGSM 方案相比于传统OGSM 方案所需信噪比分别改善了约5 dB 和8 dB，而且改善后的误码率曲线不会重合，这是由于(6-4-2)LCED-OGSM 方案相比于(5-4-2)LCED-OGSM方案ψ值更大，增加光学天线数量使可选的天线组合范围变大，进而误码率性能表现更优。相比于(5-4-2)LCED-OGSM 方案，(5-4-3)LCED-OGSM 方案的误码率性能表现更差，说明当激活的光学天线数Na增加时，系统误码率性能会明显恶化，这是因为接收端必须正确地估计更多数量的光学天线，增大了检测光学天线索引号出错的概率。

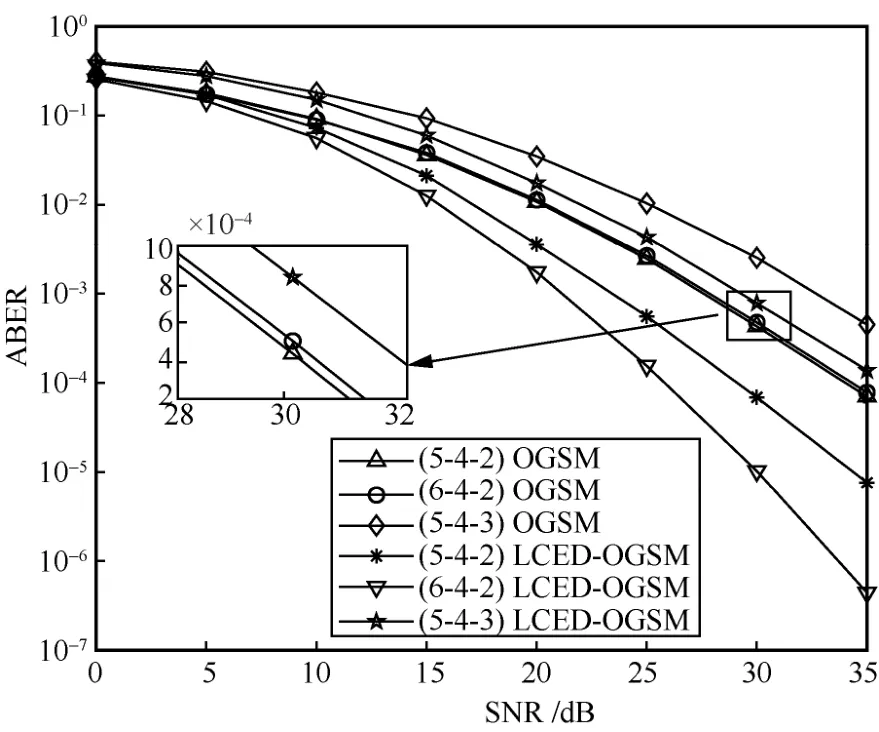
图6 不同Nt和Na对系统误码率性能的影响

不同调制阶数对系统误码率性能的影响如图7所示。仿真条件如下：ξ=1.1，Nt=4，Nr=4，Na=2，强湍流。由图7 可知，OGSM 方案和LCED-OGSM 方案都是在4-QAM 时误码率性能最好。对于OGSM 方案，当 ABER=1 ×10-4时，相较于16-QAM 和32-QAM，采用4-QAM 时的信噪比增益分别约为3.1 dB 和2.8 dB。采用本文提出的LCED算法之后，信噪比增益分别约为4 dB 和6.5 dB，说明调制阶数越高，OGSM 方案和LCED-OGSM 方案的误码率性能越差，这是因为随着调制阶数的增大，星座点之间的间隔变小，进而导致信号域检测误差变大。此外，由图7 可知，本文所提LCED 算法对低阶的OGSM 方案的误码率性能改善更加明显。

图7 不同调制阶数对系统误码率性能的影响

ACAS 算法和EDAS 算法是射频中经典的天线选择算法，本文将其应用于改进型OGSM 方案并与本文提出的LCED 算法进行比较。不同算法的误码率性能对比如图8 所示。仿真条件如下：Nt=4，Nr=4，Na=2，M=4。

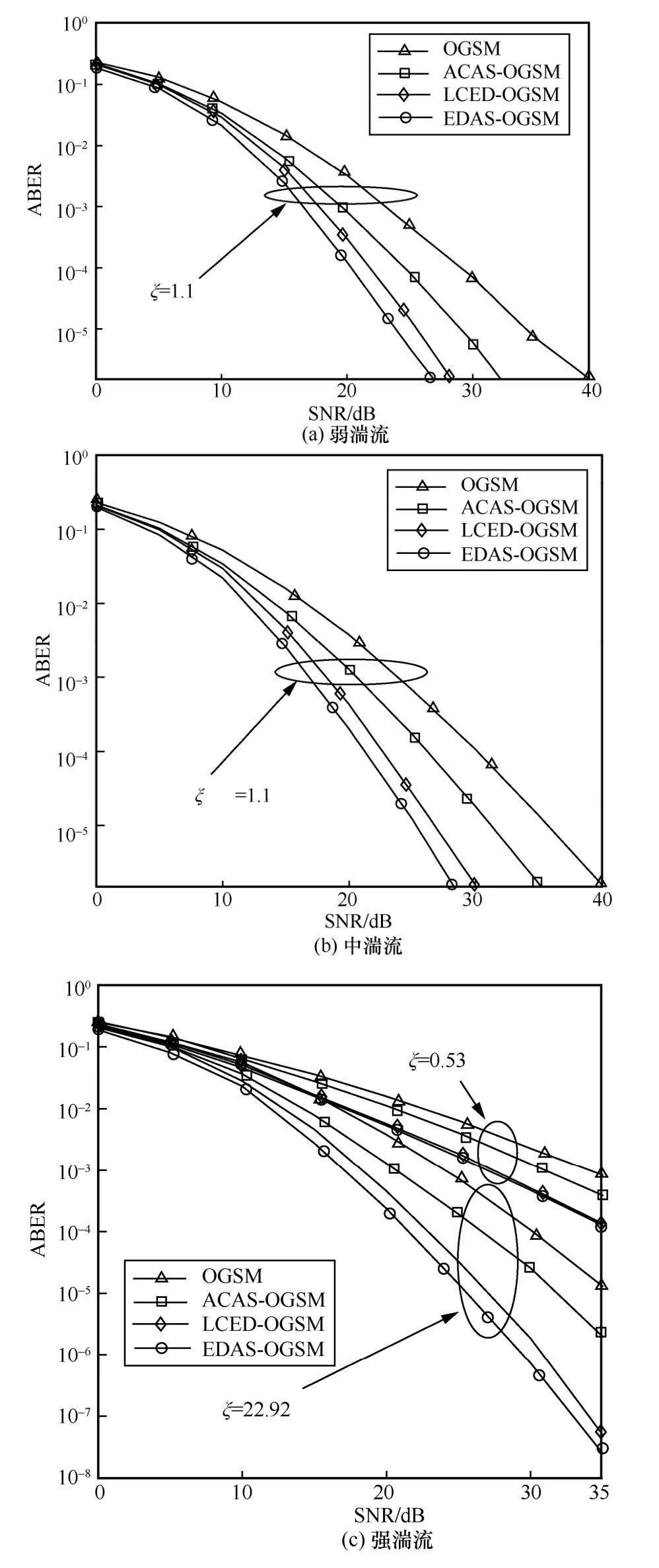
图8 不同算法的误码率性能对比

由图8 可知，本文所提LCED-OGSM 方案在不同湍流与指向误差条件下均优于传统OGSM 方案和ACAS-OGSM 方案。在图8(c)中，当ξ=22.92、ABER=1 ×10-5时，本文所提LCED-OGSM 方案信噪比约为 26 dB，相较于传统 OGSM 方案和ACAS-OGSM方案，信噪比增益分别约为9 dB和5 dB。虽然与最优的EDAS-OGSM 方案相比，本文所提LCED-OGSM 方案的信噪比损失约为2 dB。但如表2 和表3 所示，本文所提方案在复杂度方面占据更大的优势。当ξ=0.53时，相比于ξ=22.92的情况，3 种算法对OGSM 系统性能的改善程度都有所下降，但此时本文所提LCED 算法与最优EDAS 算法的性能非常接近。可见，在不同湍流情况下，本文提出的LCED-OGSM 方案的误码率性能都明显优于传统OGSM 方案和ACAS-OGSM 方案；与最优EDAS-OGSM 方案相比，在误码率性能相近的同时还大幅降低了复杂度。

5 结束语

针对现有OGSM 方案使用预先固定天线组合集导致空间资源浪费以及系统误码率性能受限的问题，本文提出了一种低复杂度的天线选择LCED算法。该算法充分利用CSI，从天线候选集中删去信道状态较差的天线组合，保留最优天线组合集，不仅充分利用空间资源，还有效改善了系统的误码率性能。同时，采用可表征所有湍流强度的Málaga信道，综合考虑指向误差和信道衰落的影响，分别考虑信号域和空间域，推导了OGSM 的系统误码率上界。仿真结果表明，相较于传统OGSM 方案，本文所提改进型OGSM 方案在不同湍流强度和频谱效率条件下明显提高了系统误码率性能；增加光电探测器的数量可提高接收分集增益，有效改善系统的误码率性能；相较于EDAS 和ACAS 天线组合集选择算法，所提LCED 算法实现了复杂度和误码率性能的折中，更适用于大容量、高速率的FSOC。

附录1 空间域APEP 的推导

根据文献[21]，在检测光学天线索引时，索引号j被错检成i的成对错误概率（PEP,pairwise error probability）为

其中，k表示级数求和的范围，其值为0 →∞的非负整数。re的矩母函数（MGF,moment generating function）为

其中，φ(Nr)表示φ的Nr-1次卷积。对式(28)进行拉普拉斯逆变换可得到ℓ 的PDF

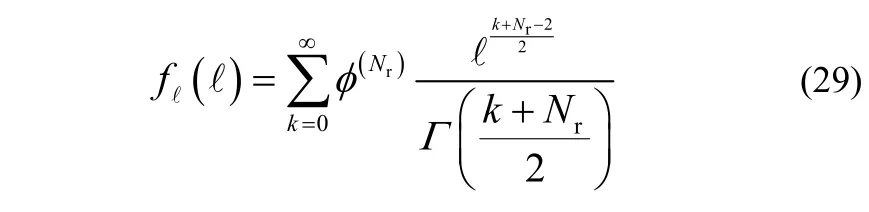
因此，空间域的APEP 为