复合材料层合结构悬臂梁振动特性试验

李虹熹，周清华，张 凯

(江南造船(集团)有限责任公司, 上海 201913)

0 引 言

目前，复合材料已广泛应用于新型民用飞机、高速列车、船舶等高新技术产业，受到研究开发人员的青睐。复合材料的主要特性为固有频率低、阻尼小、刚度低和质量轻等，可有效控制和降低机械噪声[1]，是工程领域中各类悬臂结构制造的理想材料。

国内外学者对于复合材料层合梁振动特性的研究主要集中在理论、数值仿真和试验等3种方法。JING等[2]基于Reddy理论，研究黏性夹层梁的振动特性。杨帅等[3]分析竖直方向弹性约束悬臂梁的固有频率。KAHYA等[4]基于一阶剪切变形理论，采用五节点单元分析层合梁的屈曲及振动特性。PANDA等[5]根据一阶剪切变形理论，分析温度和湿度对纤维层合梁振动特性的影响。THAI等[6]指出一阶剪切变形理论可以适用于中厚梁的自由振动分析，但所得计算结果的精度较差。SWAMINATHAN等[7]开展三阶理论研究并加以改进，其优势主要在于未知变量的数目与一阶变形理论相同。GIUNTA等[8]为研究层合梁的振动特性，分别基于3种不同的理论进行分析。黄凌志等[9]为获得更精确的层合板自由振动固有频率，推导并提出一种改进的高阶剪切变形理论。牛超[10]采用锤击法开展隧道空洞检测的试验研究。杨和振等[11]采用试验方法研究不同的环境条件对复合材料层流梁振动特性的影响。

上述国内外研究现状表明全球各国学者在理论法方面所做的研究最多，试验法也有涉及，但考虑试验仪器设备各不相同，得到的试验数据也千差万别。研究针对复合材料层合结构悬臂梁开展不同方法的试验，通过将悬臂梁简化为单自由度系统模型，测试悬臂梁的低阶频率并与理论精确解对比分析误差，得出一种能较好地适用于复合材料层合结构悬臂梁振动测试的试验方法。

1 理论分析

1.1 复合材料层合梁振动参数分析

如图1所示：考虑铺层总数为N层的层合梁，由2种材料交替铺设，铺层角度为0，用L、b、h分别表示层合梁的长度、宽度和厚度。

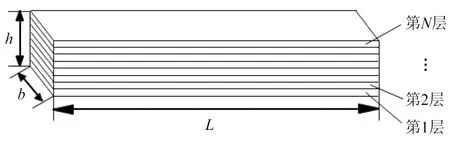
图1 复合材料层合梁几何参数

根据Timoshenko梁理论，得：

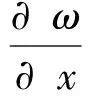
(1)

式中：ω为梁的横向挠度；φ(x)为不计剪力情况下的挠度曲线倾角；β(x)为同一截面上中心轴的剪切角。

假设各铺层结构的横向挠度ω相同，同时假定各层没有初始沿x方向的位移，且各层中面上拉伸所产生的位移关于悬臂梁的厚度方向z为线性。设梁的总旋转角为φ(x)，则对第i层：

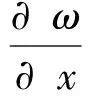
(2)

ui=liφ(x)

(3)

式中：ui为第i层梁的挠度；li为第i层梁的长度。

第i层的弯矩、轴力和剪力可表示为

(4)

(5)

(6)

式(4)～式(6)中：Ei为第i层x方向的弹性模量；Ii为第i层梁对y轴的惯性矩；Ai为第i层梁的横截面积；Zi为第i层梁的厚度；ki为剪切修正因数；Gi为第i层梁的x-z平面的剪切弹性模量。

根据Hamilton原理，第i层梁的势能为

(7)

式中：φ为梁的总旋转角。

整体梁的势能为

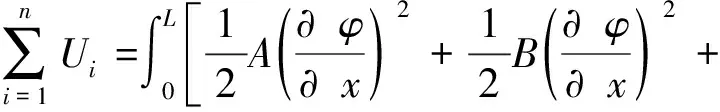
(8)

同样，可求得梁的整体动能为

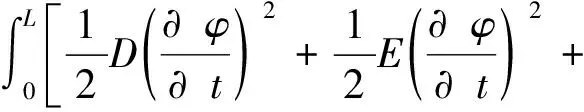
(9)

根据文献[12]可得到梁的自由振动方程：

(10)

(11)

设自由振动方程的解如下：

ω(x,i)=ω(x)sin(ωt+φ0)

(12)

式中：φ0为初始位置时梁的旋转角。

φ(x,t)=φ(x)sin(ωt-φ0)

(13)

将式(12)代入式(10)得：

(14)

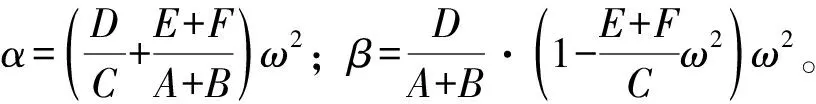
由此解得：

ω(x)=Aisinλ1x+B1cosλ1x+C1sinλ2x+

Dicosλ2x

(15)

式中：A1、B1、C1、D1为任意常数；λ1、λ2为2个特征值。

同样，将式(13)代入式(11)得：

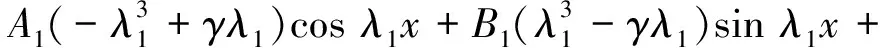
(16)

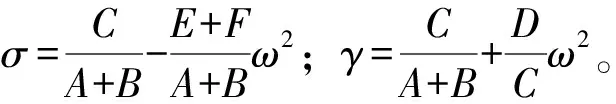
式(15)和式(16)即为复合材料层合梁振动方程的通解。

计算悬臂梁应满足的边界条件为

ω|x=0=φ|x=0=0

(17)

(18)

须令通解中：

(19)

解得：

cosλil·cosλil=1,i=1,2,3,…,n

(20)

方程的前3个根为

(21)

代入(16)得：

(22)

式(22)为悬臂梁的频率方程，由此可求得复合材料层合结构悬臂梁的各阶频率。

1.2 低阶固有频率值

纤维布层合梁一般至少由2种材料、多层0°交替铺设，任意相邻的2层纤维布经胶层粘贴固定，制作简单，可采用热压罐或普通压机直接热压工艺成型。采用的复合材料悬臂梁分别为玻璃纤维布层合梁和碳纤维布层合梁，梁的尺寸均长为500.0 mm、宽为25.0 mm、厚为5.0 mm，平均密度分别为1 800 kg/m3和1 600 kg/m3，玻璃纤维布层合梁铺层厚度为0.4 mm，碳纤维布层合梁铺层厚度为0.3 mm，具体材料参数如表1所示。

表1 复合材料层合梁主要材料参数

根据式(17)，结合表1层合梁的主要材料参数，可分别计算式(8)和式(9)中未知变量A、B、C、D、E和F的值，由此分别得出玻璃纤维层合结构悬臂梁与碳纤维层合结构悬臂梁的前三阶固有频率值，计算结果如表2所示。

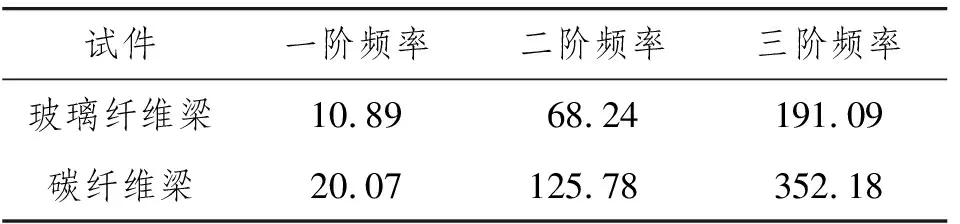
表2 复合材料悬臂梁低阶频率理论值 Hz

2 电测试验法

电测法是振动试验中较常用的方法之一，具有灵敏度高、频率范围宽、动态线性范围宽、易于检测和消除、对电磁干扰敏感等优点，室温下的静态测量误差通常为1%～3%，动态测量时的误差为3%～5%。电测振动试验根据激励方式主要可以分为阶跃激励法、锤击法和胁迫振动法，其中阶跃激励法的操作较简便，应用较广泛。根据阶跃激励法开展层合梁的振动测试试验。

2.1 试验试件

试验针对复合材料层合结构悬臂梁分别进行，设置的悬臂梁固定端深入预留长度为20.0 mm，悬臂梁外形尺寸长为500.0 mm、宽为25.0 mm、厚为5.0 mm，沿长度方向等分为5份，在宽度方向的中心点上，将悬臂梁由约束端至自由端依次标记为测点P1～测点P5，玻璃纤维层合梁和碳纤维层合梁分别如图2和图3所示。

图2 玻璃纤维层合梁实物图

图3 碳纤维层合梁实物图

2.2 试验装置及原理

试验分别选用玻璃纤维梁和碳纤维梁作为研究对象，固定在支架上，安装加速度传感器(B&K4519-003)，传感器与动态信号测试分析系统相连。采用阶跃激励，即将悬臂梁自由端抬至一定高度后瞬间松开，通过加速度传感器测试悬臂梁各测点的振动加速度响应，分析操作软件的自由衰减振动曲线识别悬臂梁的振动特性，测试原理如图4所示。

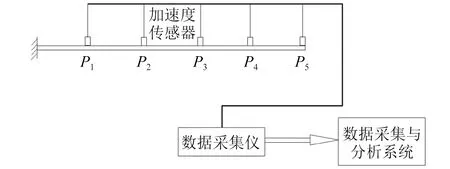
图4 电测试验法测试原理

试验均采用B&K系统的加速度传感器及数据采集仪，具体步骤为：(1)将悬臂梁固定在支架上，支架的质量相对悬臂梁来说较大，使其不影响悬臂梁的自由衰减振动；(2)将加速度传感器分别连接在数据采集仪对应的通道上，设置测量设备的采集参数和传感器参数；(3)采用阶跃激励使悬臂梁自由振动，用操作软件记录数据，测量结束后对测量结果进行分析，得到测量对象的振动频率。

分别设置3个和5个拾振点，用操作软件记录测量结果，分析悬臂梁相应的振动参数，所有工况如表3所示。

表3 阶跃激励法试验工况 mm

2.3 试验结果分析

根据阶跃激励法测得复合材料悬臂梁的低阶频率，设计不同的测点位置、数量等工况，以理论解析值作为试验值的对照基准，偏差率取试验值与理论值之差再除以理论值的百分比，试验测量结果如表4所示。电测试验法悬壁梁一阶频率测量偏差如图5所示。

综合分析表4和图5的数值可得如下结论：

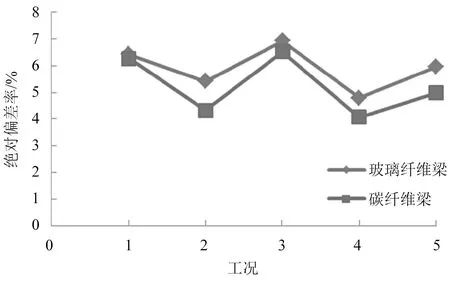
图5 电测试验法悬臂梁一阶频率测量偏差

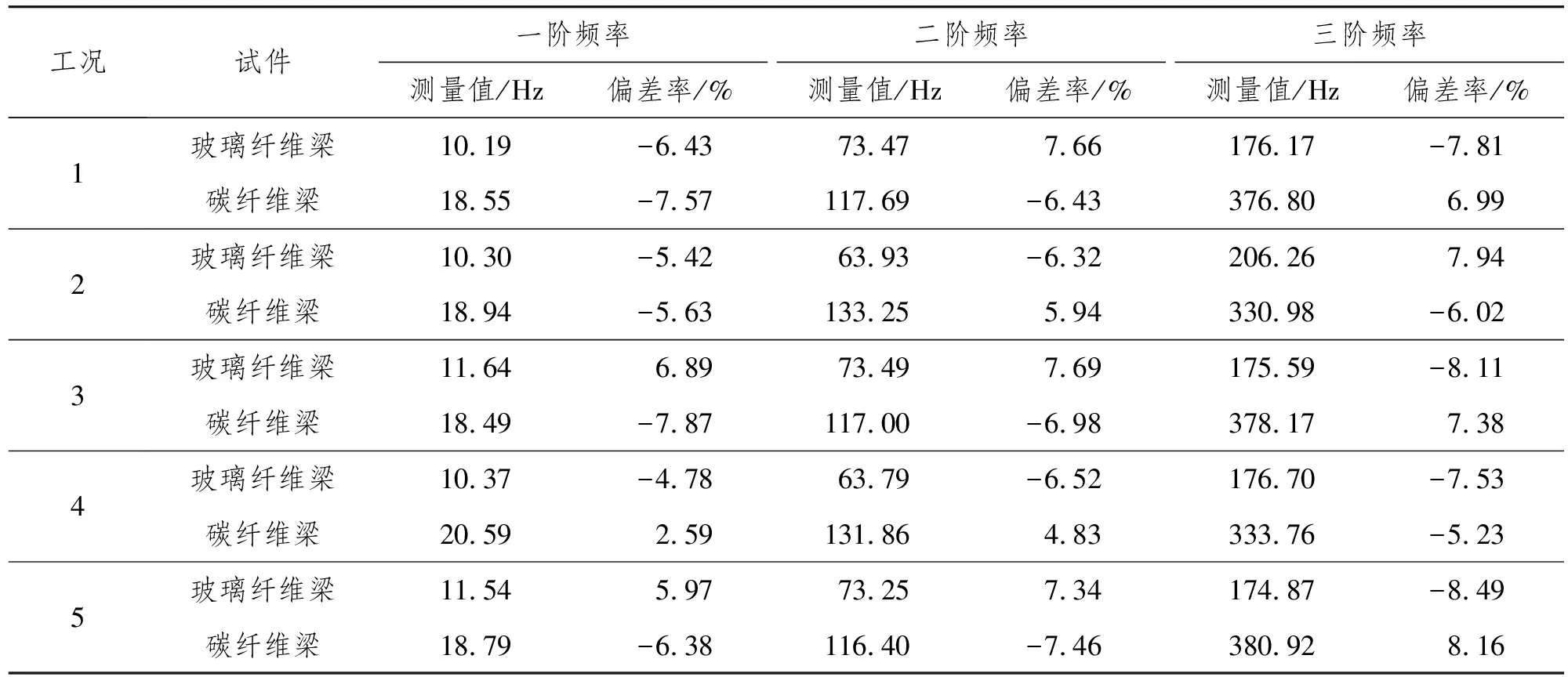
表4 悬臂梁低阶频率电测试验测量值与理论值的相对偏差

(1)采用阶跃激励法测悬臂梁的低阶频率，相对偏差率大多为负，即试验值小于理论值。试件在加工过程中产生负公差，导致测量结果始终偏小。在相同工况下，对于玻璃纤维梁所测量的低阶频率偏差总是略大于碳纤维梁，说明该试验方法更适用于碳纤维层合梁，这与层合结构梁材料参数不精确有关，层合梁在加工过程中其结构强度、刚度发生变化以及使用性受到损伤，碳纤维层合梁的各材料参数比玻璃纤维层合梁更贴合实物情况。

(2)采用阶跃激励法测悬臂梁的低阶频率，试验测量值与理论值的偏差随悬臂梁的频率阶数升高而增大。研究表明该试验方法在测量低频段时偏差更小。

(3)采用阶跃激励法测悬臂梁的低阶频率，用单测点法，P2为拾振点的最佳位置，测量偏差范围为4.00%～7.00%。

(4)采用阶跃激励法测悬臂梁的低阶频率，用多测点法，设置3个拾振点测量效果较好，测量偏差范围为4.00%～6.00%。

(5)综合分析阶跃激励法所有试验工况的测量结果，玻璃纤维梁和碳纤维梁在工况4所测得一阶频率的测量偏差均最小，分别为-4.78%和2.59%，其二阶和三阶频率也在此工况条件下的测量偏差最小，即工况4为最佳工况。

3 光测试验法

目前，电测法已广泛应用于振动测试试验之中。随着振动测量技术的成熟与完善，光测法也在材料探伤、机械系统的故障诊断、噪声消除、结构件的动态特性分析及振动的有限元计算结果验证等方面展开应用[13]。光学测量技术具有结构简单、精度高、抗压强度高、耐腐蚀、可在易燃易爆环境中连续工作、抗电磁干扰、功率范围宽等优点。通过锤击激励使悬臂梁自由振动，采用激光测振仪接收信号，搭建悬臂梁自由振动的试验装置台，设计不同类型的激振测振仪、不同的测振仪探头与试件的垂直距离和不同的采样时间等工况，开展各工况的试验并将测量结果与理论值对比分析误差。

3.1 试验装置及原理

为测量玻璃纤维梁和碳纤维梁的低阶频率，搭建试验平台，其主要由夹具、基座和压板等组成，如图6所示。试验试件与第2.1节相同。将层合梁固定在支架上，测点位置对准激光测振仪光学头，激光测振仪控制箱与动态信号测试分析系统相连。沿悬臂梁长度方向等分为10份，依次标记为测点P1～测点P10，贴上反光纸(鉴于不平整表面会影响光学头接收反射光的效果，反光纸可以减少悬臂梁本身凹凸不平的表面带来的测量误差)。采用锤击激励，通过自由衰减振动曲线识别悬臂梁的振动响应特性，试验原理如图7所示。

注：1为激光测振仪的光学头；2为激光测振仪的控制箱

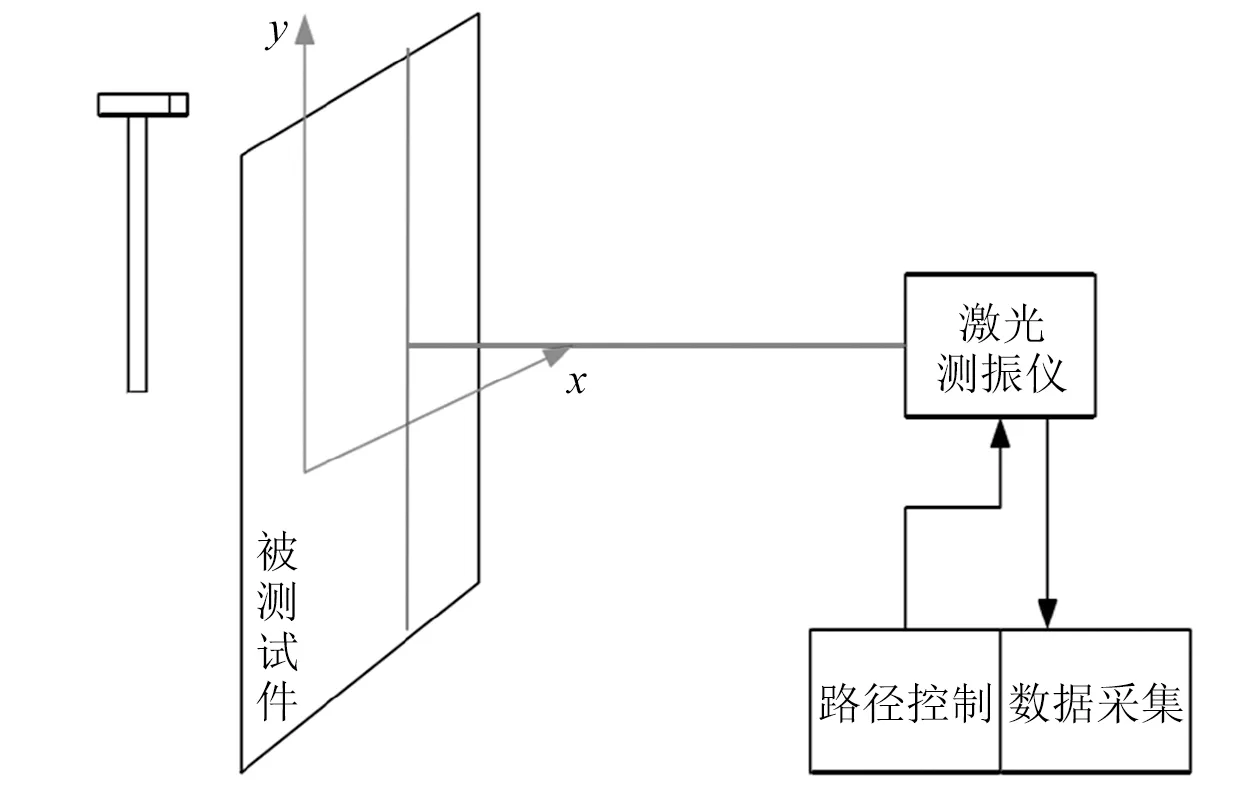
图7 激光测振法测试原理

3.2 试验工况

试验工况如表5所示，工况设计主要从如下3个方面考虑：

表5 激光测振法试验工况

(1)分别用光纤式、单点式和扫描式激光测振仪开展试验，采用操作软件记录测量结果，测得悬臂梁相应的振动参数。试验所用光纤式激光测振仪型号为LV-FS01，单点式激光测振仪型号为LV-S01(法向)，扫描式激光测振仪型号为LV-SC300。

(2)采用光纤式激光测振仪LV-FS01，改变测振仪光学头与被测试件的垂直距离，由1.0 m分别改为0.5 m和1.5 m进行试验，采用操作软件记录测量结果，测得悬臂梁相应的振动参数。

(3)采用光纤式激光测振仪LV-FS01，设置测振仪光学头与被测试件的垂直距离为0.5 m，改变采样时间步长：3 s、5 s和10 s，采用操作软件记录测量结果，测得悬臂梁相应的振动参数。

3.3 试验结果分析

根据激光测振法可测得复合材料悬臂梁的前三阶固有频率，将试验测量值与第1.2节的理论值对比，结果如表6所示。激光测振法悬臂梁一阶频率测量偏差如图8所示。

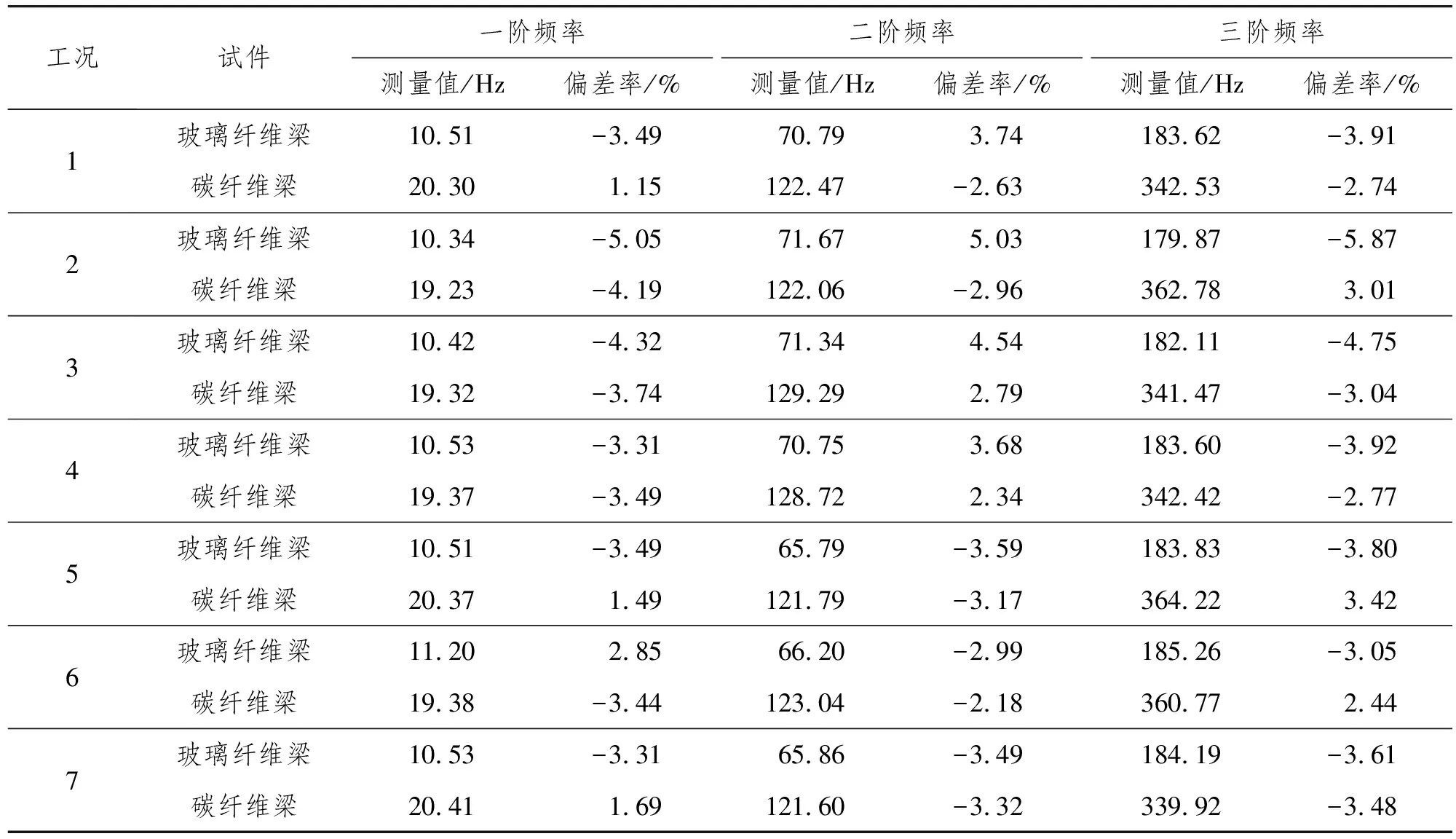
表6 悬臂梁低阶频率光测试验测量值与理论值的相对偏差

综合分析表6和图8的数值可得如下结论：

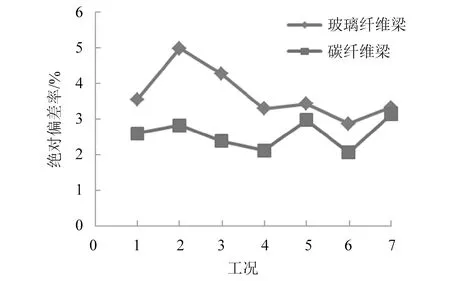
图8 激光测振法悬臂梁一阶频率测量偏差

(1)采用激光测振仪测悬臂梁的低阶频率，用单点式、扫描式和光纤式激光测振仪所测得悬臂梁的一阶频率偏差逐渐递减，偏差范围为1.00%～5.50%。由于单点式激光测振仪的测量分辨率比扫描式、光纤式激光测振仪都低，因此其测量偏差最大；扫描式激光测振仪通常用于大型结构测点数量多的试件而不适用于微小型试件；光纤式激光测振仪为测量小型悬臂梁振动参数的最佳选择。

(2)采用激光测振仪测悬臂梁的低阶频率，用光纤式激光测振仪，测振仪光学头与试件测点的垂直距离由1.0 m分别改为0.5 m和1.5 m，试验结果表明测振仪光学头距离被测试件越近，测量结果越精确，偏差范围为2.00%～3.50%。

(3)采用激光测振仪测悬臂梁的低阶频率，采样时间由3 s分别改为5 s和10 s。试验结果表明：在采样时间为3 s时，时间过短导致采集的数据不够完整、精确；在采样时间为10 s时，时间过长而易受到周围环境的影响，采集数据中混杂环境的微弱振动源会导致测量结果的偏差变大；设置采样时间为5 s测试效果最佳，测量偏差范围为4.00%～7.50%。

(4)研究结果表明，玻璃纤维梁和碳纤维梁在工况6条件下所测得一阶频率的偏差最小，分别为2.85%和-3.44%，其二阶和三阶频率也在此工况条件下的偏差最小，即工况6为最佳工况。

4 结 论

以复合材料层合结构悬臂梁的振动特性为研究对象，采用电测和光测这2种试验方法开展研究，得出结论如下：

(1)鉴于理论分析方法计算层合梁的振动参数过程繁琐、耗时长，通过刚度迭合，基于Timoshenko梁理论和Hamilton原理，将层合梁作为整体梁来考虑，推导一个简化振动方程，可快速计算复合材料层合结构悬臂梁的低阶频率，该方程亦适用于实际工程问题。

(2)无论采用阶跃激励法还是激光测振法，试验测量值与理论值的偏差随悬臂梁的频率阶数升高而增大。

(3)激光测振法的测量效果比电测试验法更好，偏差更小，原因在于光测法为非接触式测量，无附加质量的影响，测量结果的准确性更高。