基于PCA-SVM的混合气体分类研究

杨 朝， 张平平， 汪国强， 杜宝祥

(1.黑龙江大学 电子工程学院, 哈尔滨 150080；2.苏州慧闻纳米科技有限公司 研发部，苏州 215000)

0 引 言

在我国的工业领域，易燃或者有毒的气体检测技术一直是产品安全控制的重要技术，如乙醇、甲烷、一氧化碳以及硫化氢等有害气体的检测。乙醇和甲烷气体虽然没有毒，但是浓度过高的时候会引起人头晕、乏力，会对人的呼吸消化系统产生严重的危害，如果不及时进行处理，可导致人窒息死亡[1]。而一氧化碳和硫化氢气体是有毒气体，会对人的身体健康产生一系列的危害。如果在工业领域的生产过程中产生这样的气体，则会造成不可预测的后果。因此，有害气体的识别和分类问题在相关领域显得愈加重要。

针对气体的分类问题，国内外很多的学者都对此展开了深入的研究，如印度的Sunny等利用反向传播神经网络和支持向量机对丙酮和丙醇两种气体进行分类，实验表明支持向量机(Support vector machine，SVM)分类器表现良好，该研究为两种气体的分类提供了希望，但是在多种气体的分类中的效果未知[2]。Habib等利用决策树和神经网络两种算法对氨气、乙醛、丙酮、乙烯、乙醇和甲苯6种气体进行分类，能够减轻传感器漂移对气体的正确分类和识别的影响，但是实验的准确率还有待提高[3]。在国内的研究中，Xu等提出了一种基于极端随机树的混合气体检测算法，提高了分类准确率和时间效率，但是仅基于两种混合气体进行的实验，没有在多种气体混合的气体中进行实验[4]。宋海声等基于PCA-BP神经网络对甲醛和甲醇的识别研究表明，PCA方法有效降低了数据的维数，能够提高甲醛和甲醇识别分类的准确率[5]。宋婷婷等采用粒子群算法对最小二乘支持向量机模型中的相关参数进行迭代优化，构建PSO-LSSVM模型对混合气体的成分进行定性分析，对乙烯、甲烷和一氧化碳混合气体的公共数据集进行实验，识别的准确率较高[6]。由此可以看出，随着机器学习和深度学习的发展，越来越多的学者尝试借鉴机器学习分类算法的思想，从单一气体或者混合气体中提取特征，然后训练分类器实现对气体的分类。

在前人研究和总结的基础上，本文对8阵列传感器和24阵列传感器采集到的乙醇、甲烷、一氧化碳以及硫化氢的混合气体进行分类。首先，提取不同传感器对目标气体的响应值，利用PCA算法找出数据中的主要成分，用主要成分去描述数据，从而达到对提取的数据特征降维的效果；然后，将主要成分作为SVM的输入向量，构造PCA-SVM模型，并且与SVM、参数优化的BP神经网络以及PCA-BP神经网络模型进行对比。实验结果表明，PCA-SVM模型不仅能够将不同浓度的同一气体很好地分类，而且在不同浓度的4种混合气体中分类具有较高的准确度，能够解决气体分类的实际问题。

1 数据采集及来源

1.1 数据采集系统

数据采集系统可以分为两部分：第一部分是模拟信号处理部分，主要包括气体传输系统和气体传感器部分，气体经过气体传输系统随之进入气体传感器的室内，气体传感器阵列对进入的气体会产生一系列的化学反应并将气体浓度以电信号输出[7]；第二部分是数字信号处理部分，主要包括信号预处理、特征提取以及模式识别部分，气体传感器阵列产生的电信号进入数字信号处理部分进行后续的处理[8]。先将模拟信号产生的数据进行滤波，去除一些无用的信息，再进行特征提取，将提取出来的信息送入模式识别单元中分析得出结果。数据采集系统的结构如图1所示。

图1 数据采集系统结构图

1.2 数据来源

对不同浓度的甲烷、一氧化碳和硫化氢气体进行了分析。其中包括用8阵列传感器采集的甲烷气体(1 000、3 000、6 000和9 000 ppm)、一氧化碳气体(50、100、150、200和250 ppm)和乙醇气体(20、50、100和200 ppm)，以及用24阵列传感器采集的甲烷气体(1 000、2 000、3 000、5 000和8 000 ppm)、一氧化碳(100、150、200、250和300 ppm)和硫化氢(0.2、0.5、0.8、1.0和1.5 ppm)。同一浓度的相同气体是在相同的温度和湿度条件下获得的，不同种气体的不同浓度都是在不同的温度和湿度条件下获取的。把每一个传感器采集的数据以及温度湿度等作为数据的特征，故用8阵列传感器采集的气体都含有13个特征值，把一种浓度的气体作为一类，那么把8阵列传感器采集的气体分为13类。同样，24阵列传感器采集的气体都有27个特征值，将24阵传感器采集的气体分为18类。

2 算法描述

采用PCA对所采集的气体特征进行主成分分析，选取主要的成分，其主要是利用降维的思想，把多个指标转换为少数的几个综合指标，将降维后的数据作为SVM的数据输入，从而进行数据分类。

2.1 主成分分析

主成分分析技术(PCA)主要是将数据的维数降低，把多个指标转换为少数的几个综合指标，在简化数据集上有广泛的应用，它是一个线性变换，是将原始的数据变换到一个新的坐标系统中，使得任何数据投影的第一大方差在第一个坐标上(称为第一主成分)，第二大方差在第二个坐标上(称第二主成分)，以此类推。主成分分析主要应用在减少数据集的维数，同时，保持对方差贡献最大的特征，保留数据主要的方面，最终的目标是用较少维数的主要特征来描述数据集[9-10]。

PCA的主要原理是将原始的数据样本投影到一个新的空间，将原来的样本数据空间经过数据变换矩阵变到新空间坐标下，新空间坐标由原始数据样本中不同维度之间协方差矩阵中几个最大特征值对应的前几个特征向量组成，较小的特征值对应的特征向量将作为非主要成分被去掉，就可以达到提取一些主要特征来代表数据，降低数据复杂度的目的[11]。

PCA算法流程主要分为以下几个步骤：

步骤1：通过n次采样得到的m维数据构成矩阵X∈Rn×m,具体形式如式(1)所示：

(1)

(2)

步骤3：计算其样本数据维度之间的相关度，使用协方差矩阵C，如式(3)所示：

(3)

步骤4：计算协方差矩阵C特征值和特征向量，并按照特征值从大到小排列，如式(4)所示：

(4)

步骤5：根据降维的要求，比如降到k维，取前k个向量组成降维矩阵P，如式(5)所示：

P=(P1,P2,…,Pk)T,P∈Rk×n

(5)

步骤6：通过变换矩阵P对原样本X进行坐标变换，从而达到数据降维和提取特征的目的，如式(6)所示：

Y=X·P,Y∈Rk×m

(6)

PCA重建误差的计算：

在投影完成之后，要对投影的误差进行重建，通过式(7)和式(8)来计算降维之后的信息损失：

(7)

(8)

将Error1与Error2比率记作η，通过式(9)计算：

(9)

通过η来衡量数据降维之后的信息损失,根据η的大小来选择数据合适的k值。

2.2 支持向量机

支持向量机(SVM)是在20世纪90年代由Cortes和Vapnik开发的一种监督机器学习技术，它把样本空间映射到高维特征空间，构造最优分类超平面的高维空间。传统的支持向量机是用来实现二分类，SVM是在寻找和分类线平行而且接近两类样本的最优分类线，从而达到对输入的数据进行二分类的目的[12]。

给定一个样本(xi,yi),i=1，2，3，…，n，xi是输入向量，而且满足xi∈Rd，yi是样本的标签，而且满足yi∈{1,-1}，其中φ(x)能够将输入向量x从输入空间映射到d维特征空间的函数，那么特征空间中的分类超平面就可以定义，如式(10)所示：

wTφ(x)+b=0

(10)

式中：w=(w1;w2;…;wd)为法向量，决定了超平面的方向；b为位移项，决定了超平面与原点之间的距离。

支持向量机的思想是将建立好的超平面作为决策曲面，将两个类之间的边界进行最大化，这也是将分类问题转化为带惩罚项的最小化问题，可写成如式(11)所示：

(11)

式中：w代表权向量；ξi是将分离误差最小化的松弛变量；C代表对误差容忍度的惩罚参数，如果C的值越大，则代表分类的结果越好，但是泛化能力越低。

由于目标函数和约束条件构成了不等式的约束问题，需要引入拉格朗日函数来推导这个不等式的解，如式(12)所示：

(12)

式中：L为拉格朗日系数；αi≥0是拉格朗日乘子。

最优分类面求解问题，根据式(12)对w和b求偏导数，结合拉格朗日多项式，可以将其转化为约束优化的最大化的问题，约束函数如式(13)所示：

(13)

式中：Q为二次规划函数；K(xi,xj)为非线性映射的内积核函数，K(xi,xj)=φ(xi)·φ(xj)。

(14)

式中b*为分类阈值。

采用的核函数为高斯径向基函数(Radial basis function, RBF)核，表达式如式(15)和式(16)所示：

(15)

(16)

式中σ是由(16)中的Gamma(γ)确定的自由参数，γ的值越大，训练的结果越好，但泛化能力也越低。

不同的支持向量机可以由不同的核函数构成，如线性核函数、径向高斯核函数和多项式核函数，之前的研究表明，径向高斯核函数与其他函数相比较有明显的优势，因此，选择RBF作为SVM的函数，SVM在结构上与神经网络相似，SVM的结构如图2所示，隐藏层中的每一个节点对应一个支持向量，并且输出的是支持向量的线性组合[13]。对于在训练过程中多分类的问题，将某一类的样本作为一类，其余的样本作为另一类，如果样本有k个类别，那么就构建k个支持向量机，当用SVM算法进行分类的时候，将未知样本分类到函数值最大的类别中。

图2 SVM的结构图

3 气体分类模型构建

基于PCA算法和SVM模型原理，本文构建了PCA-SVM模型应用于气体的多分类问题。虽然大多数支持向量机的输入参数与气体分类的过程相关，但是气体数据中的固有冗余影响气体分类的速度和准确性，因此为了提高分类的速度和精度，采用PCA的方法通过减少与类别不相关的特征来降低数据的维度，为了降低气体数据特征的维数，PCA调用了线性变换，通过对数据进行线性组合求出协方差矩阵的最大k个特征值对应的特征向量，原数据集有n个特征值，在尽量减少对原始数据影响的情况下进行降维处理，在k个特征值中选择方差最大的p1为第一主成分，如果p1不足以代表原来n个特征值代表的信息，那么继续选取第二主成分p2,如果p1和p2的累积贡献量不能满足需要，那么继续选取，直到满足实际的需要为止，而且p1,p2,…,pn互不相关，因此可以构造T个主成分，构造公式为：

(17)

在支持向量机的训练和学习的过程中，支持向量机通过参数的优化来提高识别精度，而且通过对几种核函数的比较，选择高斯RBF核作为核函数，同时对RBF中的惩罚因子C和γ采用10倍交叉验证技术来优化，才能使SVM模型得到最准确的分类方法[14]。PCA-SVM的分类模型如图3所示。

图3 PCA-SVM分类模型

4 实验与分析

为了验证所提出方法的有效性与可行性，与SVM、BP神经网络以及PCA-BP神经网络进行了气体分类方法对比。

4.1 气体数据集

数据集采用的是某公司采集的气体数据来验证本文提出的模型的有效性，主要利用8阵列的传感器和24阵列的传感器来采集气体的数据，其中包括用8阵列传感器采集的不同浓度的甲烷、乙醇和一氧化碳气体，24阵列传感器采集的不同浓度的甲烷、一氧化碳和硫化氢气体。采集气体的信息如表1所示。

4.2 实验结果分析

采用两个混合气体的数据集来分别进行实验，第一个数据集是8阵列传感器采集的不同浓度的甲烷气体(1 000、3 000、6 000和9 000 ppm)、一氧化碳气体(50、100、150、200和250 ppm)和乙醇气体(20、50、100和200 ppm)的混合气体，随机取样本650个，共有13类样本，每个样本含有13个特征。第二个数据集是采用24阵列传感器采集的不同浓度的甲烷气体(1 000、2 000、3 000、5 000和8 000 ppm)、一氧化碳气体(100、150、200、250和300 ppm)和硫化氢气体(0.2、0.5、0.8、1.0和1.5 ppm)的混合气体，随机取样本1 800个，共有18类样本，每个样本含有27个特征。利用SVM分类模型和PCA-SVM分类模型对气体的原始数据进行分类对比，考虑到分类器是有监督的，因此，从每个数据集中随机抽取70%的样本作为训练集，其余的30%的样本作为测试集。

为了验证本算法的有效性与优越性，首先使用不降维且完整的第一个数据集的气体数据作为特征参数，将支持向量机与高斯RBF作为核函数的模型用于气体分类，分类的准确率为95.897%。为了提高识别的准确度，在将气体特征数据作为支持向量机的输入数据之前，先利用PCA对数据进行降维，对数据进行降维最重要的就是选择降低的维数，需要选择最合适的k值，那么就用数据重建误差来衡量，k的值由1取到13。通过比较，当k的值由1取到6时，数据重建误差是逐渐减小的，当k的值由6取到13时，重建误差稳定在0.439 9，所以把k=6作为最合适的k值，说明降维后的数据特征代表了原始样本集中的大部分特征，在一定程度上消除了参数的冗余。部分k值对应的误差比率如表2所示。经过PCA降维后的数据特征作为SVM模型的输入，训练SVM模型后，基于PCA-SVM的气体分类的准确率为98.974%。SVM分类准确率和PCA-SVM分类准确率分别如图4和图5所示，其中，横坐标代表测试集的样本编号，纵坐标代表测试集样本的类别。红色的点代表每个测试样本的真实类别，蓝色的点代表测试样本预测的类别。如果蓝色点落在红色点上面，那么就代表这个样本分类准确，如图4绿色的框所示。如果蓝色点没有落在红色点上，则代表样本分类错误，如图4红色的框所示。通过统计正确的分类样本数，可以计算分类准确率。通过比较图4和图5可知，SVM错分样本数8个，计算的分类准确率为95.897%，PCA-SVM错分样本数2个，计算的分类准确率为98.974%，PCA-SVM模型相对于未降维的SVM模型，准确率提高了3.077%。

表2 不同k值对应的误差比率

图4 SVM模型

接着利用SVM模型和PCA-SVM模型在第二个数据集上分别实验，将SVM与高斯RBF作为核函数的模型用于气体分类，准确率为98.704%，结果如图6所示。利用PCA-SVM模型进行分类时，首先要选择合适的k值，然后再进行分类，k的值由1取到27。通过比较，当k的值由1取到14时，数据重建误差是逐渐减小的，当k的值由14取到27时，重建误差稳定在0.365 8，所以把k=14作为合适的k值。部分k值对应的误差比率如表3所示。PCA-SVM模型进行分类的结果如图7所示，准确率为100%。通过比较图6和图7可知，SVM错分样本数7个，分类准确率为98.704%，PCA-SVM错分样本数0个，分类准确率为100%，PCA-SVM模型相对于未降维的SVM模型，准确率提高了1.296%。

表3 不同k值对应的误差比率

图6 SVM模型

图7 PCA-SVM模型

为了验证本文提出的PCA-SVM模型的有效性与优越性，不仅和利用RBF作为核函数的SVM作比较，而且还和BP神经网络模型以及PCA-BP神经网络模型进行了比较，如今BP神经网络是被广泛应用的模型之一。BP神经网络包含输入层、隐藏层以及输出层。神经网络各层的层数和结点数是由输入气体的特征个数和数据量的大小决定的。BP神经网络算法的实现过程需要信号的正向传播和误差的反向传播，正向传播时，输入样本从输入层进入，逐次经过隐层，最后到达输出层。如果实际输出值与期望输出的值相差太大，则将误差进行反向传播，误差的反向传播是将误差逐层经过隐层，并且将误差分给每一层的所有单元，从而获得每一层的误差信号去修正各单元的权值[15]。

将BP神经网络模型和PCA-BP神经网络模型分别在两个数据集上进行实验，通过不断调整优化BP神经网络的参数，得到的分类结果如表4所示。由表可知，在含有13个气体特征的第一个数据集和在含有27个特征的第二个数据集上应用BP神经网络模型和PCA-BP神经网络模型，从准确度方面考虑，在第一个数据集上，分类准确率提高了3.077%，在第二个数据集上，分类准确率提高了2.889%。从性能方面考虑，用均方误差来衡量，由图8可知，BP神经网络的最小均方误差为0.014 9。由图9可知，PCA-BP神经网络的最小均方误差为0.009 4，无论是从分类的准确率的角度比较，还是从神经网络模型的性能的角度比较，PCA-BP神经网络模型都优于BP神经网络模型。通过以上的结论可知，PCA无论是应用在SVM模型上还是应用在BP神经网络上都能提高分类的准确率。

表4 BP神经网络与PCA-BP神经网络模型的对比

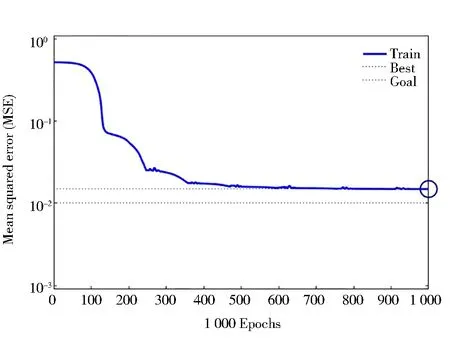
图8 BP神经网络的MSE

图9 PCA-BP神经网络的MSE

由表5可以看出，PCA-SVM分类模型的分类准确率更高，在第一个数据集上准确率能达到98.974%，在第二个数据集上准确率能达到100%，分类结果优于SVM模型、BP神经网络模型以及PCA-BP神经网络模型，因此，PCA-SVM分类模型能够解决8阵列传感器和24阵列传感器采集到的混合气体进行分类的实际需求。

表5 不同分类模型分类准确率比较

5 结 论

采用PCA-SVM模型对混合气体进行分类。在原有气体特征的基础上利用PCA对数据降维，将降维后的气体特征作为SVM的输入从而进行分类，并且与不对数据降维的支持向量机、BP神经网络模型和PCA-BP神经网络模型进行对比，经过实验验证，利用主成分分析对输入数据进行降维，提高了支持向量机算法的分类准确率，能够满足8阵列传感器和24阵列传感器采集到的混合气体进行分类的实际需求。随着大数据的快速发展，将支持向量机与主成分分析相结合，能够减少数据的冗余，提高模型的分类效率，广泛地应用于多种混合气体分类的研究。