具有媒介的多种群炭疽传播模型的动力学分析

韩梦洁, 刘俊利, 刘白茹

(西安工程大学 理学院，西安 710048)

0 引 言

炭疽是一种人畜共患的急性传染病[1]，能够引起家畜和食草动物的突然死亡，造成巨大的经济损失。世界上多个国家都曾爆发炭疽疫情，在中东、非洲等一些发展中国家尤为常见，此外，炭疽也能用于生物战争[2]。因此，研究炭疽的传播动态具有非常重要的意义。

食草动物是炭疽最主要的感染源，如牛和马等。在研究动物种群中炭疽的传播动态时，一些学者提出了几种数学模型。1983年，Hahn等以动物吸入环境中的孢子病毒感染炭疽为背景，在动物种群中建立了炭疽传播的微分方程模型[3]。2013年，Friedman等提出了一个带有局部扩散的微分方程模型，模型既考虑了环境污染和动物死亡，又考虑了动物以染病尸体为食的情况[4]。在炭疽爆发期间，血食性蝇被认为是一种潜在的疾病传播媒介[5]。2013年，Baldacchino等研究了血食性蝇传播炭疽的方式，指出血食性蝇能够从呕吐物和内脏中分离出炭疽杆菌，进而通过叮咬传染易感动物[6]。2017年，Mushayabasa等在动物种群中建立炭疽传播模型时加入了血食性蝇，研究了所建模型的理论结果与媒介对炭疽传播和控制的影响[7]。随着对炭疽疾病的深入研究，很多文章表明尽管炭疽是一种食草动物疾病，但是接触炭疽孢子病毒的人和动物都有感染炭疽的风险。如1980年，McKendrick研究了当血食性蝇存在时，食草动物与人之间的传播机制[8]。2010年，Fasanella等研究了炭疽在不同物种之间的传播方式，表明了在炭疽爆发期间，血食性蝇发挥着重要的作用[9]。

虽然已经有很多文章研究了炭疽在动物种群之间的传播，但是多种群之间炭疽的传播很少受到关注。为了寻找控制炭疽传播的有效措施，本文根据食草动物-血食性蝇-人三个种群之间的炭疽传播机制，建立了一个具有媒介的多种群炭疽传播模型。

1 模型的建立

根据炭疽在食草动物-血食性蝇-人之间的传播机理建立如下炭疽传播模型。将模型分为9个仓室，t时刻易感食草动物的数量为Sa(t)，染病食草动物的数量为Ia(t)，则动物的总数量Na(t)=Sa(t)+Ia(t)。P(t)表示t时刻环境中孢子病毒的数量，C(t)表示t时刻感染炭疽死亡的动物尸体的数量。假设t时刻易感血食性蝇的数量为SH(t)，染病血食性蝇的数量为IH(t)，则血食性蝇的总数量FH(t)=SH(t)+IH(t)。对于人，考虑易感者(Sh(t))、染病者(Ih(t))和恢复者(Rh(t))三类，且总数量Nh(t)=Sh(t)+Ih(t)+Rh(t)。为了简便，使用FH(t)-IH(t)替代SH(t)，根据以上假设，建立如下模型：

(1)

式中：假设Λa为食草动物的输入率；Λh为易感人群的输入率；bH(FH)为血食性蝇的出生率函数；di(i=a,H,h)为食草动物、血食性蝇和人的自然死亡率；δa为染病动物的因病死亡率；δh为感染炭疽的人的因病死亡率，ηC是染病动物尸体释放孢子病毒的速率；孢子病毒对易感动物的传染率为βPa。

由于染病动物的粪便中携带孢子病毒，因此ηa表示染病动物释放孢子病毒的速率。假设孢子病毒的衰减率为k，染病动物尸体的腐烂率为μ，则1/k为每克孢子病毒存活的平均时间，1/μ是染病尸体完全腐烂的平均时间。血食性蝇叮咬染病动物后携带孢子病毒，之后在叮咬动物的时候可以传染食草动物，则βaH表示染病动物对血食性蝇的传染率，βHa表示染病的血食性蝇对易感动物的传染率。人不仅能够通过吸入孢子病毒感染炭疽，而且能够通过接触染病动物皮毛等制品或食用染病动物感染炭疽，则βPh、βah和βCh分别表示孢子病毒对易感人群的传染率、染病动物对易感人群的传染率和染病动物尸体对易感人群的传染率。此外，大部分的炭疽感染者都能恢复[10]，则ρI表示染病者的恢复率，恢复者的免疫丧失率为ρR。假设δa≥0，其他参数为正常数。

下面证明系统(1)的非负有界性。

定理1对于系统(1)的任意初值(Sa(0),Ia(0),P(0),C(0),FH(0),IH(0),Sh(0),Ih(0),Rh(0))∈Ω，当t≥0时系统(1)存在唯一的非负有界解，其中

此外，系统(1)的正向不变集为：

证明由微分方程基本理论可知，对任意的初值(Sa(0),Ia(0),P(0),C(0),FH(0),IH(0),Sh(0),Ih(0),Rh(0))∈Ω，系统(1)在其最大存在区间[0,T)，T≤∞上存在唯一的非负解。

将系统(1)中的Sa(t)和Ia(t)相加可得：

(2)

则对任意的t∈[0,T)，Na(t)有界。同理可得，对任意的t∈[0,T)，Nh(t)有界。由于

(3)

根据比较定理可知，P(t)和C(t)在t∈[0,T)上有界。

血食性蝇增长所满足的方程：

(4)

在文献[11]中曾经提到出生函数bH(FH)的假设如下：令血食性蝇的出生率函数bH(FH)=B(FH)FH，对FH∈(0,+∞)，假设B(FH)满足以下3个性质：

注：在生物学文献中满足性质(A1)～(A3)的出生率函数B(FH)的例子有：

(ii)B2(FH)=be-aFH，a>0，b>dH

2 平衡点分析

平衡点是研究系统(1)动力学性质的基础，本节将讨论系统(1)的平衡点的存在性。

当血食性蝇不存在时，当且仅当Rp>1时，系统(1)存在地方病平衡点E2=(Sa2,Ia2,P2,C2,0,0,Sh2,Ih2,Rh2)，其中

下面计算系统(1)的地方病平衡点。

记m1=βPaP+βHaIH，m2=βaHIa，m3=βPhP+βChC+βahIa，此时系统(1)的正平衡点的分量为：

把上面的表达式代入到m1和m2的表达式中，得：

(5)

(6)

将式(6)代入式(5)中，得：

(7)

下面仅考虑m1≠0的情况。式(7)两边同时除以m1，可得：

(8)

3 平衡点的稳定性和疾病的持久性

无病平衡点表示疾病的消亡，地方病平衡点表示疾病最终会长期存在而成为一种地方病。研究平衡点的稳定性能够为控制炭疽的传播提供理论依据。本节将从理论上讨论系统(1)的平衡点的稳定性。

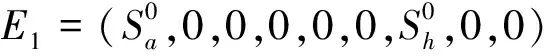
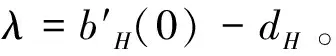
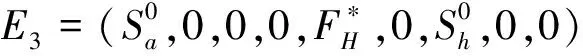
(1)如果R0<1成立，则平衡点E3是局部渐近稳定的；

(2)当R0>1时，正平衡点E*存在。若δa=0成立，则平衡点E*是局部渐近稳定的。

证明对于平衡点E3，它的特征方程为：

(9)

其中I4×4是四阶单位矩阵，且

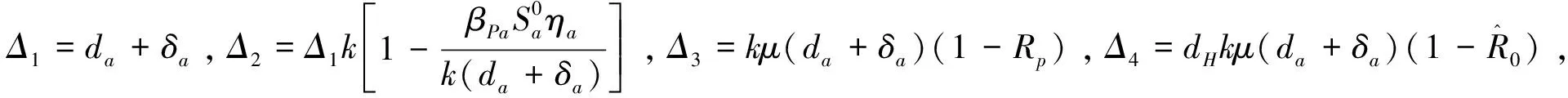
由于地方病平衡点E*的稳定性不易证明，因此在证明其稳定性时只考虑δa=0的情况。

对于平衡点E*，当δa=0时，其雅克比矩阵的形式为：

其中

由分块矩阵的性质可知，J(E*)的特征值由J11和J22的特征值组成。J11的特征方程为:

(10)

其中I4×4是四阶单位矩阵，且

-M2的顺序主子式为

此时-M2的顺序主子式均大于0，又因为-M2的主对角线元素均大于零，非主对角线元素非正，则-M2是M-矩阵。由文献[13]可知，M2的所有特征根均具有负实部。由于方程(10)的另外两个特征根均小于0，则矩阵J11的所有特征根均有负实部。容易证明-J22是M-矩阵。因此J22的所有特征根均具有负实部,从而矩阵J(E*)的所有特征根均具有负实部，则E*是局部渐近稳定的。定理证毕。

局部稳定性只能描述当初始值位于平衡点附近时系统的动力学行为，而全局稳定性则可以将系统的初始值扩大到更大范围来研究解的长期行为。下面将分析系统(1)的平衡点的全局稳定性。

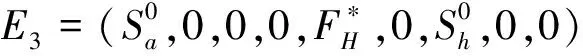
(1)当R0<1时，如果FH(0)>0，则E3在Ω内部是全局渐近稳定的;

(2)当正平衡点E*存在时，对于δa=0，若FH(0)>0成立，则E*在Ω内部是全局渐近稳定的。

(11)

考虑系统(11)的辅助系统：

(12)

(13)

f1(ρυ1,ρυ2,ρυ3,ρυ4)>ρf1(υ1,υ2,υ3,υ4)，f2(ρυ1,ρυ2,ρυ3,ρυ4)=ρf2(υ1,υ2,υ3,υ4)

f3(ρυ1,ρυ2,ρυ3,ρυ4)=ρf3(υ1,υ2,υ3,υ4)，f4(ρυ1,ρυ2,ρυ3,ρυ4)>ρf4(υ1,υ2,υ3,υ4)

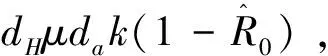
(14)

定理4中讨论了δa=0时地方病平衡点的全局稳定性，对于δa≥0的一般情况，正平衡点的全局稳定性不易得到，下面的定理给出了R0>1时疾病的持久性。

定理5若R0>1，则存在ε>0，使得对于系统(1)中具有初值条件Ia(0)>0，P(0)>0，C(0)>0，IH(0)>0，Ih(0)>0的解(Sa(t),Ia(t),P(t),C(t),FH(t),IH(t),Sh(t),Ih(t),Rh(t))满足

由于定理5的证明方法与文献[15]类似，因此这里不再赘述。

4 控制措施

在传染病建模中，依据所建模型的理论结果与实际生活中传染病的病例数据研究疾病的控制措施是极其重要的。结合文献[16]中给出的参数值，利用弹性指数和目标再生数两种方法寻找食草动物-血食性蝇-人之间炭疽传播的有效控制措施。

4.1 弹性指数

基本再生数R0在炭疽控制方面起着非常重要的作用。当R0>1时炭疽流行成为一种地方病持续存在，R0<1时炭疽消亡，因此，通过研究R0寻找控制炭疽传播的有效措施极其重要。在许多流行病学研究中，通常使用弹性指数研究基本再生数R0对参数的敏感性。此时，变量为R0，根据文献[16]的计算方法可得弹性指数为：

显然，上述所有的弹性指数都有一个确定的符号，即基本再生数R0随着参数βPa、ηa、ηC、βaH和βHa的增加而增加；随着参数k、μ、dH、da和δa的增加而降低。

为了从数值上确定系统(1)的弹性指数，下面以土耳其的人炭疽病例数为例，对系统(1)的相关参数值进行估计。2004年土耳其接种疫苗的动物数量为60 387[17]，感染炭疽的动物数量为376[17]，其中337只动物病死[17]，动物出生率为1.216 7/年[16]，由于染病动物与死亡动物的数值均是在已接种动物中监测得到的，则Sa(0)=60 387，Ia(0)=376，C(0)=337，从而食草动物的常数输入为Λa=Sa(0)×1.216 7=73 472.862 9，染病动物的因病死亡率为δa=C(0)/Ia(0)=0.896 3/年。假设血食性蝇出生率函数为Ricker型，即B(FH)=be-aFH。血食性蝇一生产卵量约500粒，生命周期约30天，则b=6 083.33/年，dH=12.166 7/年。据统计，土耳其2004年总人口为7 115万人[18]，出生率为19.9‰[18]，人均寿命为70岁，则Λh=7.115×107×19.9‰=1 358 965，dh=0.014 3/年。由于染病者恢复后不会永久免疫，则ρR=1/年。由文献[10]和文献[18]知，参数δh=0.023 5/年，ρI=0.976 5/年，βph=0.038/年，βah=0.952/年，βCh=0.5/年。其余参数值见表1，根据世界卫生组织发布的土耳其1996～2004年人炭疽病例数[18]进行拟合，对参数ηa、βaH和βHa进行估计，具体参数值如表1所示。

依据上述参数值，计算R0的所有参数的弹性指数，具体值如表1所示。

表1 基本再生数R0的弹性指数值

由表1可知，参数对炭疽的爆发或消亡有不同程度的影响，其中参数da、δa、dH、βaH和βHa对R0的影响最显著，因此及时对动物接种疫苗、降低食草动物的患病率和因病死亡率、尽可能消除苍蝇的繁殖地点、对苍蝇使用杀虫剂、减少染病苍蝇的数量是控制炭疽传播最有效的措施。此外，虽然上述理论分析中没有涉及人群对炭疽传播的影响，但是对人群普及教育、不食用染病动物等措施能够降低易感人群感染炭疽的风险，对炭疽传播也有一定的抑制作用。

4.2 目标再生数

为了量化根除炭疽而需要控制的特定种群的百分比，依据文献[19]描述的方法进行计算。首先计算食草动物进行疫苗接种的目标再生数。假设公共卫生部门决定对食草动物进行疫苗接种，此时目标集S={(1,1),(1,2),(1,3),(1,4)}，则目标再生数为：

(15)

血食性蝇是传播炭疽的一个重要媒介，在叮咬染病动物之后携带孢子病毒，进而传染食草动物，因此消灭血食性蝇的数量、降低血食性蝇的传染率是控制炭疽的一个有效方法。此时目标集S={(4,1)}，根据文献[19]的计算方法可得目标再生数为：

(16)

根据式(16)可得，如果Rp<1，则通过消灭1-1/T41比例的血食性蝇能够根除炭疽。依据表1得T41=6.874 6，因此，为了使R0小于1，需要消灭1-1/T41=85.45%的血食性蝇。

5 结 论

本文研究了具有媒介的食草动物和人的炭疽模型，分析了模型的动力学行为。根据土耳其1996～2004年人炭疽病例数估计了模型参数值，并研究了基本再生数关于参数的敏感性，同时，依据目标再生数将控制措施数值化。结果表明，对超过85.05%的动物接种疫苗或消灭85.45%以上的血食性蝇都能够根除炭疽。