基于多目标PSO-ACO融合算法的无人艇路径规划

杨 琛，陈继洋，胡庆松，张 铮，牛锋杰

(上海海洋大学 工程学院 , 上海 201306)

如今水产养殖规模持续扩大，养殖过程中用工成本高、劳动力短缺等问题日渐尖锐，养殖设备机械化、自动化的要求越来越高，水产养殖业正逐步向智能化、现代化和协同化的方向转变[1]。河蟹等“惰性”生物在养殖过程中，传统的人工遍历式饵料投喂方式，常常存在局部点投喂不足的问题。为解决这一问题，同时提高河蟹养殖自动化程度，采用无人艇对多目标点进行全局路径规划自动投饵，实现精准作业的同时避免水体富营养化，提高投料效率和养殖收益。

路径规划技术借助搭载丰富的传感器，获取实时位姿信息以及作业环境，并在预设环境模型下利用合适的寻优算法规划出最优路径轨迹[2]。学者们针对静态问题的全局规划研究包含A*算法[3-5]、蚁群算法 (Ant colony optimization, ACO)[6-8]和粒子群算法 (Particle swarm optimization, PSO)[9-11]等。Votion等[12]在A*算法的基础上增加惩罚激励机制以此来提高多目标路径轨迹的安全性与多样性。Chen等[13]提出一种基于混沌的混合粒子群优化蚁群路径规划算法，利用切比雪夫混沌序列生成随机因子更新公式，优化调整粒子群算法参数，引入全局异步特性和精英策略，改进信息素更新方式，算法搜索速度快，但缺少自适应调整参数。杨立炜等[14]提出初始信息素阶梯分配原则和运用动态切点调整法平滑路径，解决了目标单一无法应对复杂多变的实际问题。陈劲峰等[15]通过设置节点之间的属性关系，减小搜索范围，缩小运算时间，改进一种自适应不同复杂环境的蚁群算法。董翔宇等[16]将蚁群算法的单向搜索变为双向搜索，把人工势场思想引入到启发因子中，对转移概率做了改进，证明了改进算法的优越性。张天瑞等[17]对于路径转角过大、收敛慢的问题，把转角启发函数加到节点转移概率中，提高路径选择的适应性，降低局部最小值概率，并利用遗传交叉环节进行二次优化，保证了寻优速度和路径质量。何少佳等[18]对于存在的搜寻效率低和路径不平衡等问题，利用粒子群算法的全局搜寻优点，快速得到初始信息素，方便下一步蚁群算法的路径规划，过程中对每个点进行遍历，对可行路径进行惯性优化。简而言之，启发式算法具有各自相对较好的优点，但也存在其不足。学者们通过对算法参数因子的改进、目标函数的调整和融合其他算法，提高算法的先进性与适应性。

经典规划算法易实现，但搜索效果一般；启发式算法寻优能力强，但存在其弊端。因此，为解决单一算法寻优不足，提出一种多目标粒子群-蚁群(PSO-ACO)的无人艇路径规划算法。首先建立静态水深栅格环境模型和目标函数，利用改进粒子群算法搜索路径调整蚁群算法的初始信息素，然后采用改进蚁群算法进行多目标点全局路径寻优，最后在不同环境投饵策略下仿真，验证算法的优良性。

1 问题描述与环境建模

可视图空间法、拓扑法、栅格法和Voronoi图法等几何法是当下建立环境模型的常用办法[19]。在全局路径规划下的环境建模过程中，选用恰当的建模方法有利于改善路径算法的精度与效率[20]。

1.1 一般栅格模型

最先由学者Howden[21]提出的栅格法应用得较为普遍且易于实现，其思想是将环境信息划分成一个个单元格，并对其每个单元格进行序号表示，亦可用坐标点表示。序号与坐标点能互相代替。栅格法的2种表示，如图1所示。

图1 栅格法的 2种表示Fig. 1 Two representations of grid method

栅格划分越多，环境描述越精确，但信息计算存储量也越大；反之，环境描述越模糊，计算速度越快。所以，栅格的长度选取尤为重要，一般取决于环境信息与运动对象的大小。矩阵表示为0(白色自由栅格)和1(黑色障碍栅格)。假设平面存在一点(xi,yi)，则其对应栅格点 (xa,ya)在直角坐标可表示为公式(1)：

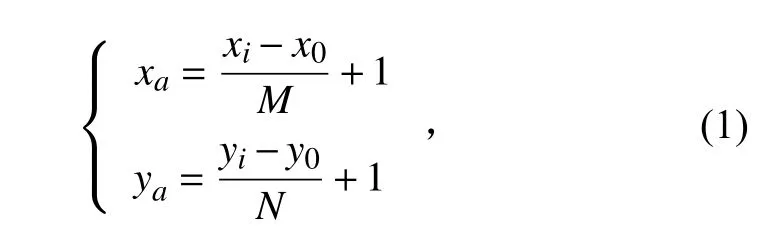
1.2 基于蟹塘环境的水深栅格模型

螃蟹养殖周期内，养殖规律和季节变化影响蟹塘水位深度。在春季养殖初期，为了促进水生物的生长，保证充足的日照和提高水温，水深一般控制在0.5～0.8 m；夏季光照充足，为保证螃蟹生长环境的舒适度，水深则保持在1.0～1.5 m。水位的高低影响航行的路径轨迹，因此引入和表征栅格位置信息；表示栅格的静态水深。通过采用样条函数的计算方法，预估每个栅格静态水深，建立静态水深栅格模型[22]：

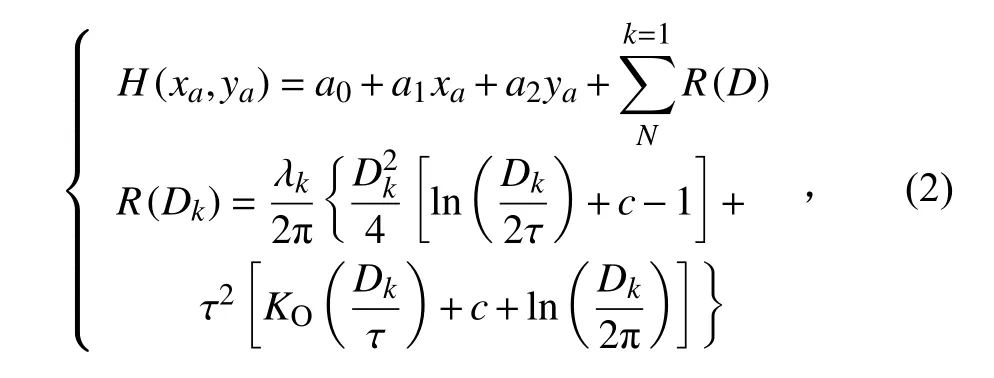
式中， H (xa,ya)表示点栅格的水位；、为通过求解线性方程组获取的系数；为规则样条插值法的函数；表示点到第个输入点的距离；c=0.517 217 5；表示修正贝塞尔函数；τ表示权重系数。

在蟹塘栅格模型中，对其不规则形状进行膨化处理，使占满整个单元栅格。蟹塘中央水位越高，栅格颜色越深。建立适合的环境模型，对无人艇的全局路径规划有着重要意义。蟹塘环境优化模型如图2所示。

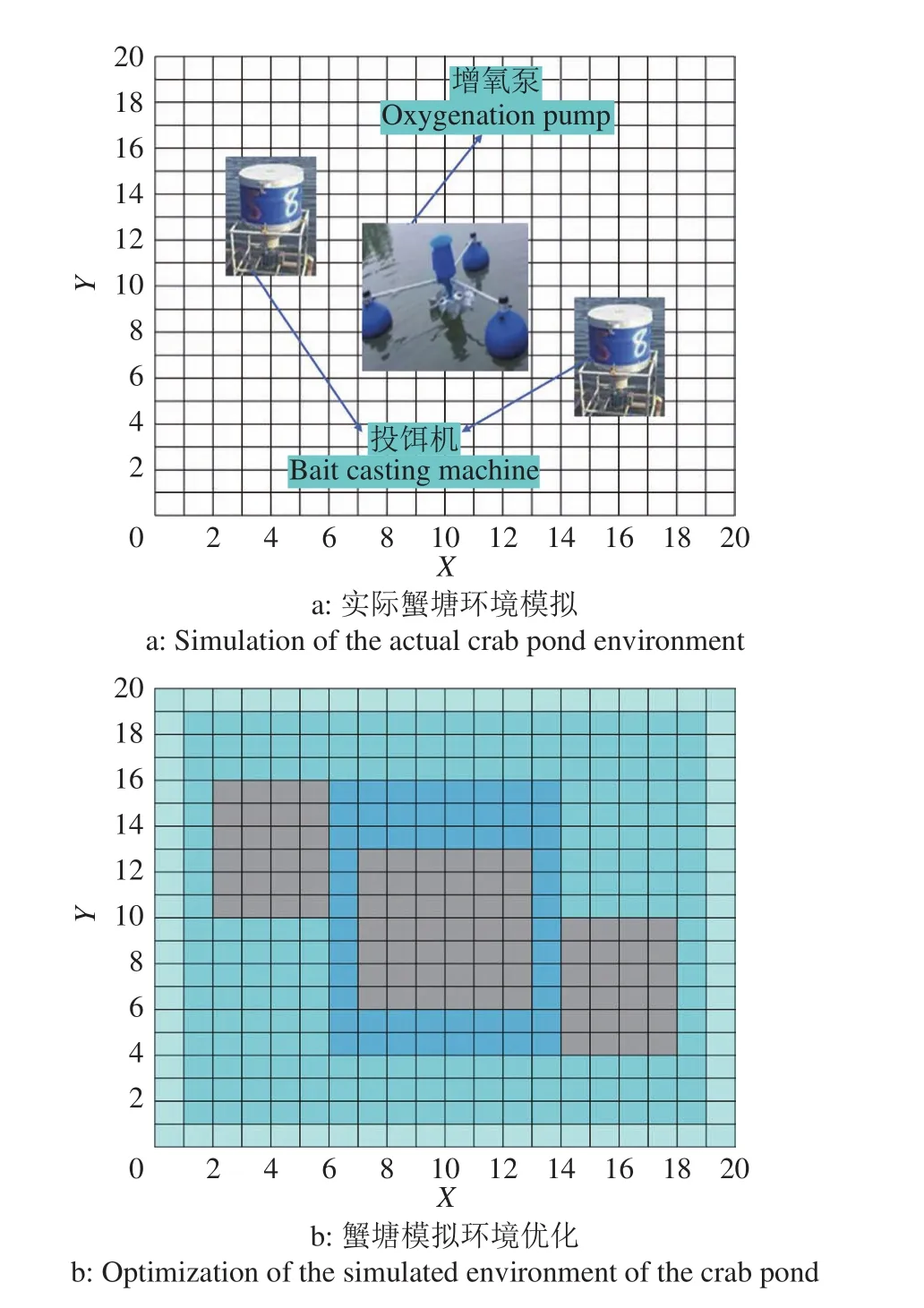
图2 蟹塘环境优化模型示意图Fig. 2 Schematic diagram of crab pond environment optimization model

1.3 目标评估函数建立

对于空间所有存在的可行解，必须建立一个目标函数来评估路径的好坏。本文结合无人艇的实际作业要求，考虑路径长度、平滑性和安全性因素，建立目标评估函数。

1.3.1 路径长度 路径长度 (L)是每一段路径的长度总和。路径长度越小越好，经济性越高。其中，是路径点的坐标，每一段的路径长度计算公式为：

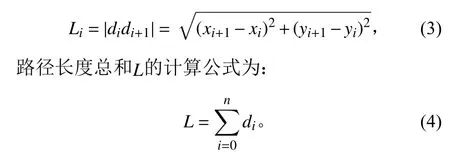
1.3.2 路径平滑性为保证规划期望轨迹应尽可能保证平滑，减少不必要的拐角。选取轨迹上的3个点。路径平滑性(艏向角的变化)()计算公式为：

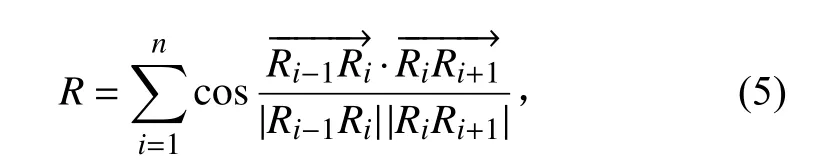
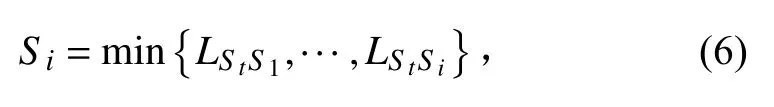
2 基于多目标 PSO-ACO 融合算法的路径规划

水面无人艇的路径规划实质上就是满足在一定约束条件下的最优化问题，规划算法多需要考虑环境的复杂性、无人艇自身的约束性以及优化指标的多样性。针对无人艇路径规划算法收敛慢、精度低的问题，对粒子群算法和蚁群算法的参数因子优化改进，提出一种多目标PSO-ACO的无人艇路径规划融合算法。

2.1 粒子群-蚁群融合算法

本文首先利用改进的粒子群算法对路径进行初始全局规划，根据粒子群算法求得的最优解，调整蚁群算法的初始信息素分布，提高算法的搜索效率；同时蚁群算法具有较好的反馈机制与搜索精度，利用改进蚁群算法进行多目标的全局路径规划。PSO-ACO融合算法流程如图3所示。

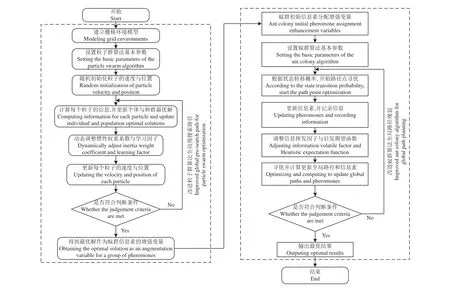
图3 PSO-ACO 融合算法流程Fig. 3 PSO-ACO hybrid algorithm flow chart

2.2 改进粒子群算法

1995年，Eberhart等[23]通过对自然界中鸟群觅食活动行为的思考，率先提出了粒子群的群智能算法。粒子群算法参数流程简单，易于实现。速度与位置代表了粒子的全部特征，其中，速度表征粒子的运动速率，位置表征粒子的方向变化。粒子在空间解运动中，不断地迭代更新自己的速度与位置，具体如式(7)所示：

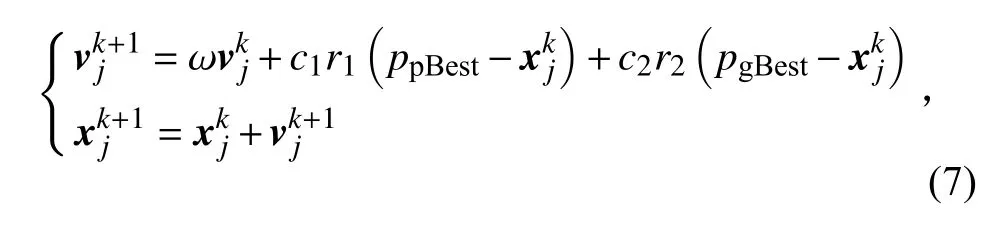
2.2.1 惯性权重的非线性自适应调整 惯性权重的取值影响着算法的寻优性能。过大时全局搜索影响较大，搜索精度较低；反之，较小时局部搜索能力较强，容易陷入局部最优。的调整多采用线性、非线性和自适应调整3种策略。为保证粒子前期搜索效率高，文献[24]采用余弦函数调整惯性权重系数的方法，并仿真对比分析了多种函数，得出凹函数优于线性函数优于凸函数，改善了迭代后期的不足。

针对粒子搜索速率慢和迭代过程易陷入局部最优的问题，本文提出采用非线性自适应调整的策略，选用非线性与自适应相结合策略，对ω进行调整。在正切函数调整ω的算法中，引入迭代系数因子()，ω取值随迭代次数的实时变化相应调整。正切函数图像随时间呈现非线性递增的趋势，起初其递增速率较慢，保证ω取较大值，便于粒子搜索全局最优解；随着迭代次数的进行，正切函数随增大而增大，使得ω取值较小，同时函数变化速率较为平缓，有利于稳定的寻优。第次迭代表达式为：

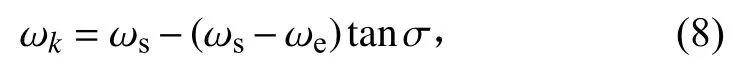
2.2.2 异步学习因子的自适应改进 在标准粒子群算法中，学习因子一般取 c1=c2=2。初始搜索阶段，为了提高算法的全局搜索性能，尽可能取较大值，取较小值；后期迭代过程中，提高群体学习因子的影响，提高算法的收敛精度。在满足c1+c2=4的情况下，文献[25]提出2种区间变化。从算法的平均适应度和整体寻优效果考虑，得出落在区间[2.25,3]和落在[1,1.75]的时候，算法的整体寻优效果较佳。本文针对学习因子对算法性能的影响，提出一种非线性自适应变化的方法,提高异步学习因子的适应性，实时计算出异步学习因子的具体值。动态调整异步学习因子，提高算法粒子的全局搜索效率和后期的寻优精度，如公式(9)所示：

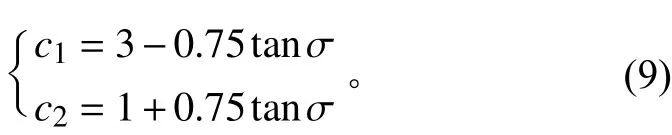
2.3 改进蚁群算法

在实际生活中，蚂蚁寻找食物会在经过的途中，留下自身的位置信息作为标记，每经过一次路径点就会累积，并将累积的信息反馈给其他蚂蚁。在观察蚂蚁觅食行为活动中，Dorigo[26]得到启示并率先提出蚁群算法。ACO算法具有全局搜索范围广，精度高等优点。路径留下的信息素密度决定了节点到节点之间的转移状态，状态转移概率的计算公式为：

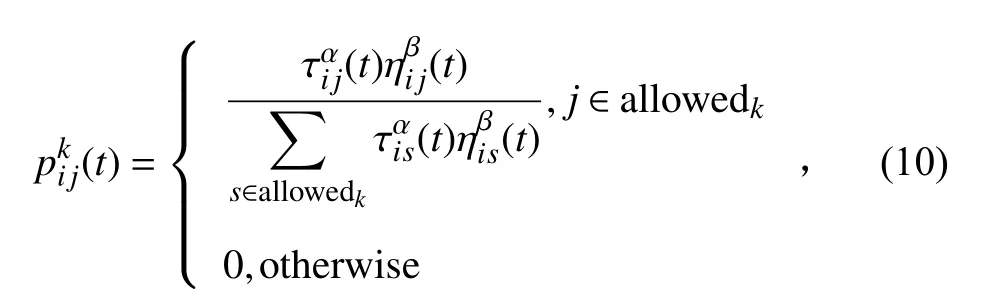
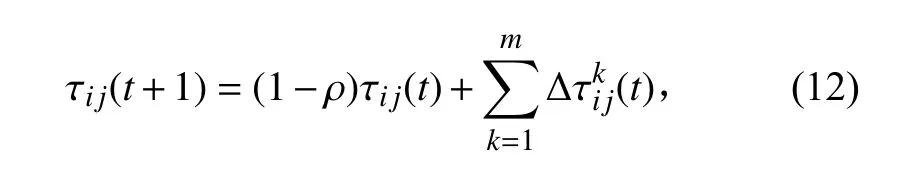
2.3.1 信息素挥发因子的优化初始信息素挥发因子要保证足够大，降低路径过程中的信息素密度，提高蚂蚁路径选择的多样性；后期迭代过程中，挥发因子随着迭代次数的增加而逐步减小，路径过程中的信息素密度逐渐增加。为了能够使蚁群算法全局寻优过程中，提高全局收敛速率和后期搜索精度，本文引入基本最小量，提出非线性地调整信息素挥发因子，提高算法搜索效率。信息素挥发因子的表达式为：

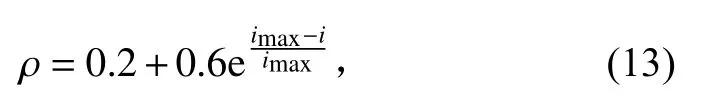
2.3.2 启发期望函数的优化为降低算法陷入局部最值的可能，本文引入A*算法的估价思想，利用节点之间的关系建立估价函数，改进启发期望函数。距离可以用节点i到节点的距离和节点的距离到目标点的距离的权重来表示。欧几里得度量计算节点间距离，具体表达式如下：

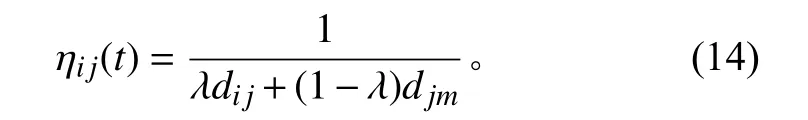
3 仿真案例分析

为验证融合算法的优良性，在2.4GHz PC，i5-1135G7，16GB RAM操作系统上运行仿真软件Matlab R2018b。

3.1 改进粒子群算法仿真分析

首先使用改进粒子群算法对多投喂点全局路径规划问题进行仿真求解。设定粒子数量1 000，最大迭代次数50，投喂点位置数目14。标准粒子群算法 ω =0.9，c1=c2=2。分别从平均运行时间、路径距离和迭代次数考虑算法的优良性，仿真结果如表1所示。

表1 2种粒子群算法仿真对比Table 1 Simulation comparison of two algorithms

算法仿真图结果对比如图4和图5所示。仿真结果表明：改进PSO算法的全局收敛速度更快，适应度值更小，全局路径长度更短，算法的效率较好。

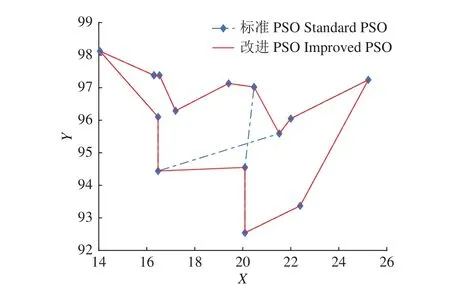
图4 多投喂点的全局最优路径Fig. 4 Global optimal path of multiple feeding points

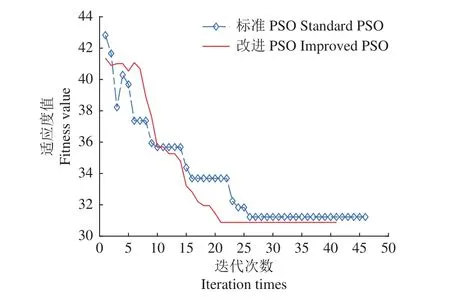
图5 对比 PSO 收敛曲线图Fig. 5 Comparison of PSO convergence diagram

3.2 简单环境单投喂点环境仿真分析

为提高算法结果的普遍性，对简单环境下单投喂点的无人艇全局路径规划问题进行了多次仿真。设置算法初始参数，栅格尺寸选用20×20，设定蚂蚁个数50，迭代次数50，单个投喂点数目为1。如表2所示，在简单环境单投喂点路径规划中，相比较于标准ACO与改进ACO，融合算法不具有路径长度的优势，但迭代次数和拐点数目均较低，整体轨迹效果较好。

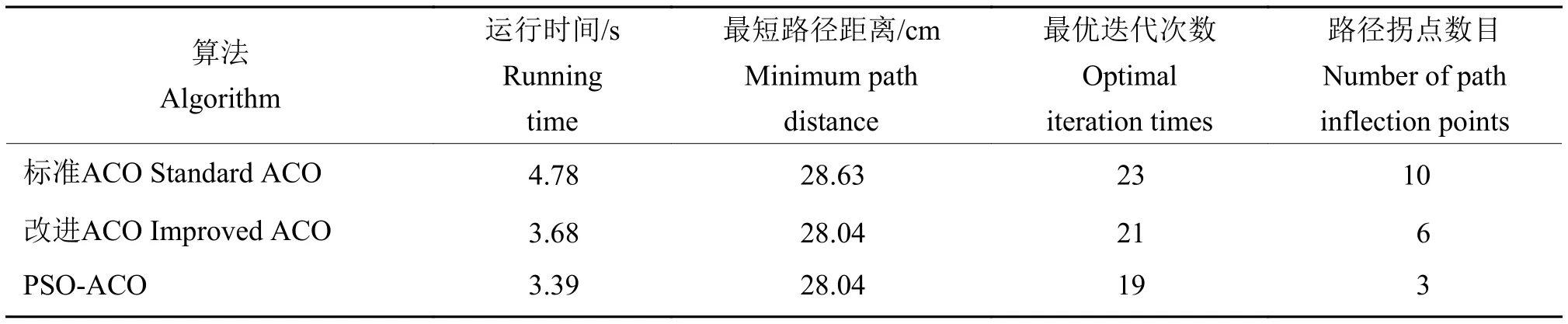
表2 简单环境单投喂点的算法仿真结果对比Table 2 Comparison of algorithm simulation results of single feeding point in simple environment

图6 和图7分别表示路径算法轨迹对比图和算法收敛曲线对比图。仿真结果表明：相较于标准ACO算法，PSO-ACO融合算法轨迹的平滑性更佳，收敛速度快，路径长度较短。

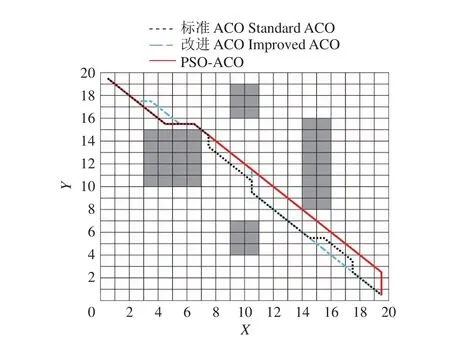
图6 简单路径算法轨迹对比图Fig. 6 Trajectory comparison of simple path algorithm

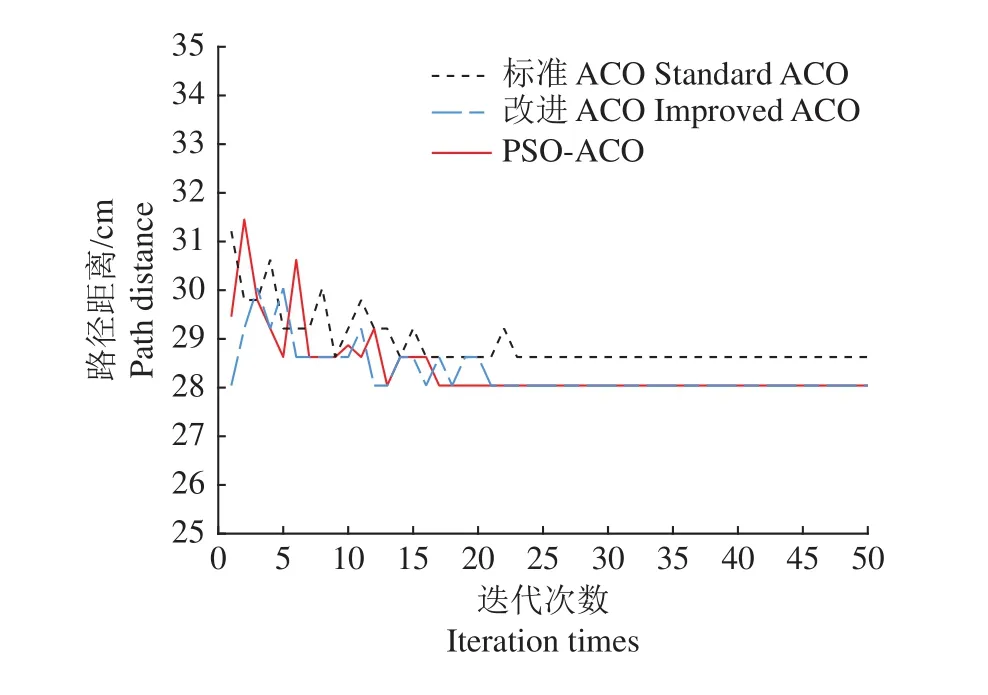
图7 简单路径算法对比收敛曲线图Fig. 7 Comparison of convergence curve of simple path algorithm

3.3 复杂环境多投喂点环境仿真分析

为了验证融合算法在复杂环境的适应性，对复杂环境下多投喂点的无人艇全局路径规划问题进行了仿真。栅格尺寸选用20×20，设定蚂蚁个数80，迭代次数200，投喂点数目为4。如表3所示，在复杂环境多投喂点路径规划中，融合算法各参数指标优势更加明显。

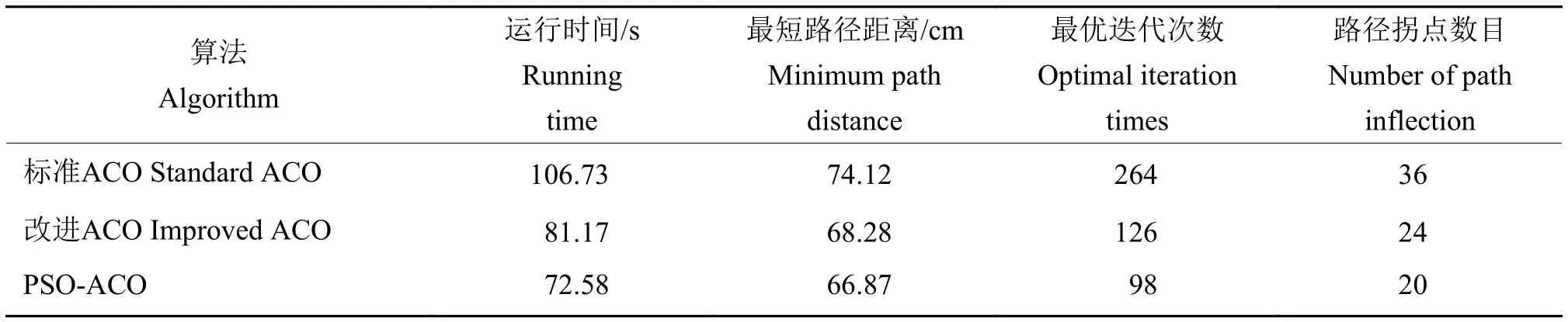
表3 复杂环境多投喂点的算法仿真结果对比Table 3 Comparison of algorithm simulation results of multiple feeding points in complex environment

图8和图9分别表示路径算法轨迹对比图和过程点收敛曲线图。融合算法路径平滑性远优于改进蚁群算法，且无危险碰撞。仿真结果显示：PSOACO融合算法的轨迹平滑性好，收敛速度快，适应度值更小，路径距离更短。

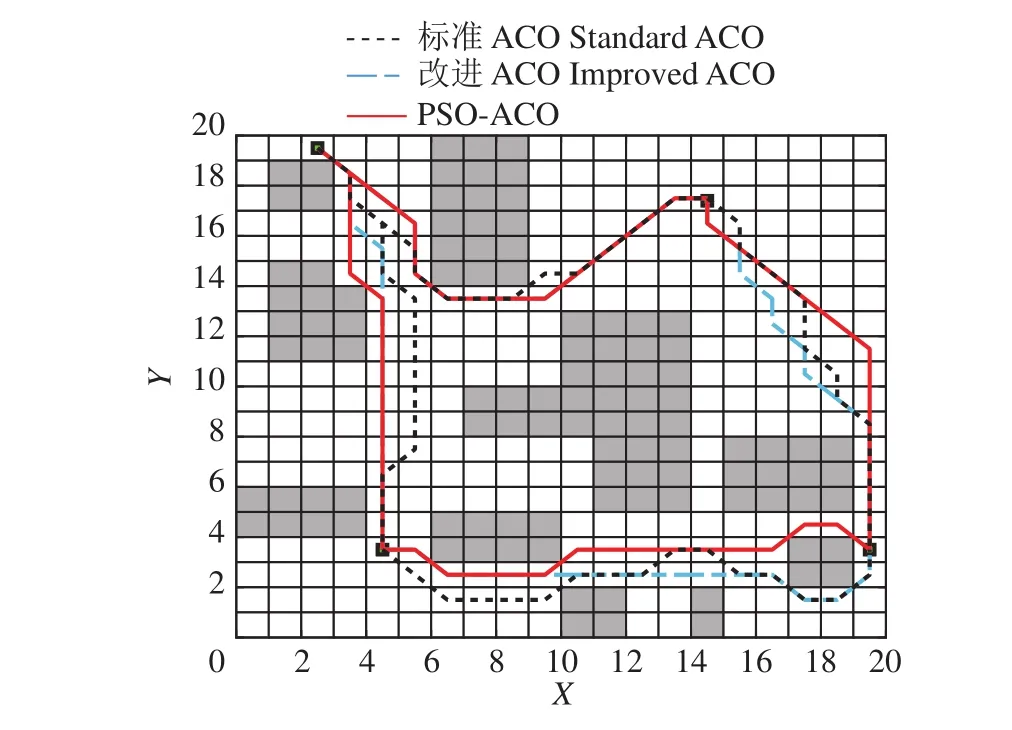
图8 复杂路径算法轨迹对比图Fig. 8 Trajectory comparison of complex path algorithm

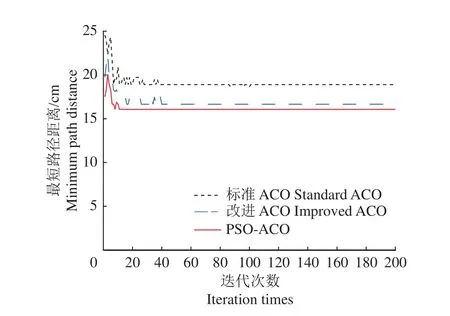
图9 复杂路径算法过程点收敛曲线图Fig. 9 Process point convergence curve of complex path algorithm

3.4 基于栅格静态水深仿真分析

鉴于河蟹养殖规律及季节环境等因素，蟹塘的水位会发生变化。水位在春季养殖初期最浅，因此只需考虑春季养殖初期水位与无人艇吃水深度的关系，当栅格的水深低于无人艇的吃水深度，则默认此栅格为浅滩区。设定某一区域栅格静态水深低于无人艇的吃水深度，并在复杂环境下对多投喂点进行全局规划。仿真结果如图10所示。融合算法不仅具有较优的规划能力，而且能够较好地规避障碍区与浅水区。

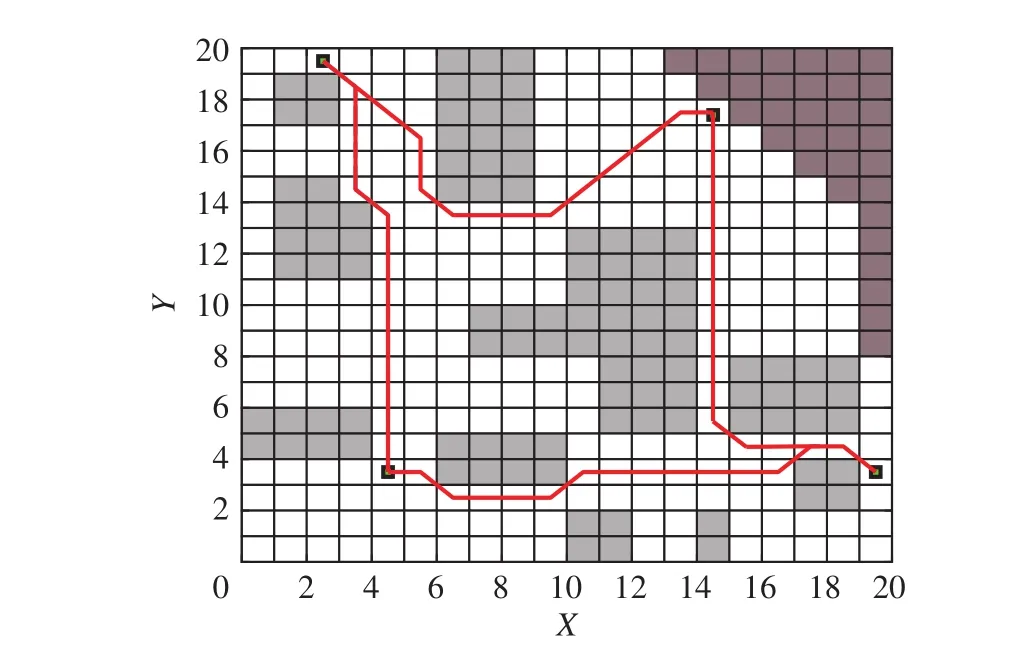
图10 静态水深下的全局规划Fig. 10 Global planning under static water depth

4 结论

针对河蟹养殖过程中，蟹塘水位环境变化以及无人艇路径规划算法收敛慢、精度低的问题，基于静态水深栅格环境模型，提出一种多目标PSO-ACO融合算法的无人艇路径规划算法。针对粒子群算法寻优精度低和蚁群算法寻优速度慢的问题，融合算法通过对自身参数的适应性调整，解决了单一算法寻优不足的弊端。在不同环境投饵策略下仿真表明，改进融合算法在对多目标路径寻优时，不仅环境适应性好，而且提高了寻优效率和精度。