基于动态能耗模型与用户心理的电动汽车充电负荷预测

张美霞，吴子敬，杨秀

（上海电力大学电气工程学院,上海市杨浦区 200090）

0 引言

由于电动汽车具有低碳、环保的优势，汽车产业发展转型是实现“碳达峰、碳中和”目标的重要途径，推动新能源汽车产业的发展是应对气候变化、推动绿色发展的战略举措。大规模电动汽车接入会影响配电网可靠性，精细的电动汽车充电负荷模型能够保证可靠性评估的准确性[1]；电动汽车作为一种特殊的可转移负荷及储能装置是连接路网交通与城市配网的载体，其本身的可移动性和空间转移的随机性受到用户出行特征与客观城市道路结构的双重影响[2]；因此，建立精细化的电动汽车充电负荷预测模型分析充电负荷的时空分布特性是研究电动汽车充电负荷对配电网影响的关键[3-4]。

针对电动汽车充电负荷预测，文献[5]提出一种基于动态交通系统的电动汽车最优路径模型，确定每辆电动汽车在使用源点-终点（origindestination,OD）分析法时的最佳路径规划，探讨了电动汽车动态通勤下的充电需求；文献[6]分析充电区域的差异性，利用马尔科夫决策对用户出行模拟，获取电动汽车充电负荷时空分布；文献[7]引入天气和温度等外界客观因素对电动汽车出行特征与出行能耗的影响，证明了气温对电动汽车出行需求有显著的影响效果。然而，在温度的处理上仅考虑单一温度条件下的充电负荷变化，在实际中温度是一个随时间变化量，若能在计及温度对充电负荷影响需要根据时间的变化精确分析温度对电动汽车充电负荷的影响会更符合实际情况；文献[8]和文献[9]综合考虑天气温度、路网交通以及充电设施之间的耦合关系，基于出行链与Dijkstra算法对用户出行过程进行规划，采用蒙特卡洛法对城市各功能区内电动汽车充电负荷时空分布进行仿真；文献[10]与文献[11]分析了用户充电差异性对电动汽车充电决策的影响，运用模糊推理法分析分时电价对用户充电行为的影响，确立了用户充电行为对充电负荷预测的影响。

基于现有的研究现状分析，电动汽车充电负荷预测存在以下3个方面的不足：

1）在预测模型上习惯将电池容量认定为一个固定参数忽略了EV能耗随环境的变化问题，给充电负荷预测结果带来了误差；

2）在用户主观意愿方面，缺少精细化的研究，用户在实际出行过程中受到实时路况与用户心理共同作用的影响，路径选择不会完全按照既定的最短路线出行。因此，电动汽车出行的路径选择不宜局限于最短路径算法，需要对用户出行的路径决策做进一步细化分析；

3）针对用户主观充电意愿，弱化了用户心理的影响，未从用户的经济水平、消费能力等角度属性考虑，缺少定量分析。

根据上述问题，提出一种基于动态能耗模型与用户心理的电动汽车充电负荷预测模型。首先对家用电动汽车和出租车的出行特征进行分析，通过蒙特卡洛法模拟不同类型电动汽车的出行过程。根据交通拥堵指数引入惩戒系数，建立基于最优策略的马尔可夫动态路径决策模型，使用户路径选择不局限于单一最短路径；在不同温度和路况下电动汽车能耗建立出行里程能耗模型，计算不同情景的实时单位里程动态能耗。引入锚定效应对用户心理进行分析，建立基于锚定效应的用户充电决策模型；最后，通过城市路网对所建模型进行验证，预测电动汽车充电需求的时空分布特点。

1 电动汽车出行时空特征

1.1 电动汽车出行模型

电动汽车出行以及充电行为的随机性为对充电负荷的时空特性有不确定的影响，同时车辆行驶路径也具有动态不确定性，使得上述变量之间的影响更加复杂。但是，电动汽车出行流量具有一定的规律性和周期性，通过考虑城市属性和不同时空场景下的出行需求，提高与车辆出行相关变量的概率分布函数在时间和空间上的相关性[12]。根据城市不同区域的功能特性以及地理信息，将城市划分为居民区（H）、工作区(W)、商业区(C)以及其他区域(O)。

家用电动汽车出行起始位置较为固定且出行具有明确的目的性，将不同的出行目的按照时间顺序进行连接就构成了私家车的出行链[13]。基于出行链理论对用户的日常出行规律进行建模，按照出行时停车节点数量将出行链模式分为简单链和复杂链，出行链中每个节点均包含有开始行驶时刻、停车时长以及停止行驶时刻等出行特征值，两节点之间包含有用户在行驶过程中的行驶里程以及行驶时间等信息。通过对NHTS2017数据库中出行数据进行概率分布拟合分析，从中选择拟合效果最好的一种概率函数代表该特征量的变化规律[14]，特征量的概率分布与参数拟合结果如表1所示。

根据GAIA计划中提供的脱敏出行数据为基础，分析电动汽车出行特征。由于网约车目的在于为城市中的居民提供便捷的出行服务，出行目的地以及出行订单数由乘客的出行需求决定，选择中国成都市区三环内的订单数据分析出租车在一天内的订单数量需求以及时间分布情况，如附录图A1所示。

电动汽车出行空间位置分布进行数据挖掘，筛选出电动汽车出行订单数据的起点位置以及终点位置，运用OD分析法获取电动汽车的出行起始点分布以及概率转移矩阵。基于图论法将现实中的道路抽象为路网拓扑图，采用OD分析法确定出租车出行的起讫点分布，通过实际订单行程中接送地点和匹配时间段获取用户出行OD概率转移矩阵[15]。根据不同时间段下的交通路况获取相应的电动汽车路段速度，计算电动汽车行驶路径所需时间，将道路邻接矩阵中的道路权值替换为行驶时间，如式(2)所示：

式中：P(G)为路网中的交通节点集合，节点数量为k；E(G)为路网中任意两节点pi，pj构成的行驶道路集合；ΨG为道路行驶时间邻接矩阵，表述各个节点与路段行驶时长tij之间的对应关系。

1.2 基于最优策略的马尔可夫动态路径决策模型

马尔可夫决策模型主要包括5个关键要素：决策时刻集Γ、状态集S、行动集A、状态转移概率p以及收益目标函数R。在某一决策时刻t(t∈Γ）下，决策者在状态i(i∈Γ）采取行动a(a∈A(i))，决策者选择行动a可获得收益为R(i,a)；在下一个决策时刻t+1(t+1∈Γ），系统的状态由概率分布为p(j∣i,a)决定；将这五重组{Γ，S，A(i)，p(j∣i,a)，R(i,a)}记作一个马氏决策过程，其中转移概率与收益仅取决于当前的状态与决策者采取的行动，与过去的历史无关[16]。

针对离散时间决策时刻有限阶段的马氏决策问题，选取决策时刻集Γ={0,1,…, N-1}，0＜N＜∞，在最后一个决策阶段N时不需要进行决策行为，在进行决策时采取的决策规则序列记为策略π，所有策略的集合称为策略集，记作Π，决策者在每一时刻进行决策时会获取一系列收益，将收益进行累加记为决策模型的效用函数VN，如式(3)所示：

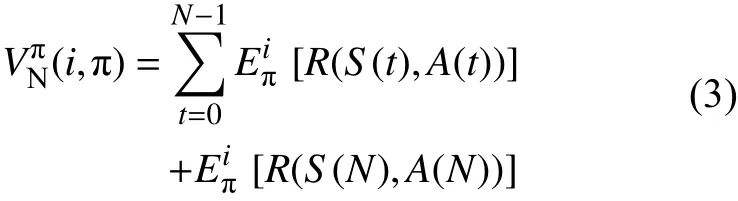
式中：S(t)，A(t)为决策时刻t时的状态与行动；R(S(t)，A(t))为t时刻获取的收益；R(S(N)，A(N))是过程的终止收益。虽然决策过程已经结束，决策者不需要再进行决策行为，但是仍可以获得系统剩余价值。

如果从策略集Π中选取一个策略π能使得效用函数VN为最优函数，则选取策略π为最优策略解。基于Bellman最优化原理可知，在任意状态下从最优行动集中选取任意行动，对于下一个决策时刻而言剩余的决策规则序列组成的策略集仍为最优策略，因此可以通过收益向后递归的方式得到决策模型的效用函数VN，其递归函数：

式中：j为下一个决策时刻t+1时的状态。

用户在道路选择上优先选取道路畅通的路段，对于交通拥堵指数值越高的路段，行驶速度越低，行驶时间越长，用户选择意愿越低。为了保证用户在出行时可以避开拥堵路段，并考虑到实际中用户决策时局部的信息不对称、对路况不熟悉以及自身心理原因，会影响决策时作出“逆向选择”，使用户决策不局限于单一最短路径，引入惩戒系数λ，如式：

式中：λt,k为决策时刻t道路k的惩戒系数；Itp,t为决策时刻t交通拥堵指数；Itp,max为参考路段交通拥堵指数最大值。

用户出行时的路径决策步骤如下：

1）用户在出发之前，选定出行目的并将规划好的最短出行路径记为πd，最短出行路径中各路段记为参考路段ld，路网节点中未被选取的路径集合选为备用路径集，记为Ak；

2）当到达决策状态i，即道路节点i时，用户会以参考路段ld的路段长度Ld、交通拥堵指数Itp,d以及惩戒系数λt,d为参考，消去备用路径集中的交通拥堵指数高于Itp,d的路段；

3）将备用路径集中的备选路段以路段长度Lk与参考路段长度Ld进行比较，计算各路段惩戒系数对路段的状态转移概率的影响，各路段状态转移概率pt：

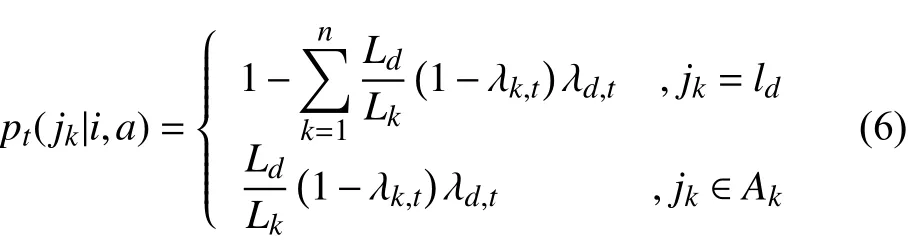
式中：jk=ld表示决策行动按照原计划进行最短路径选择的状态转移概率；jk∈A表示决策行动选择备选路段的状态转移概率。

2 电动汽车动态能耗（DEC）模型

2.1 电池容量模型

电动汽车在正常行驶过程中受到道路等级、路况交通、车速以及气温等外界客观因素的影响，进而影响充电负荷需求及其日常状况。通过耦合外界客观信息对电动汽车出行里程能耗的影响，建立精细化的电动汽车单位里程能耗模型。同一种电池在不同温度下的容量和充放电特性差别很大，所以采用目前主流的锂电池的实验数据为例，建立了温度与电池容量的关系[17]。

使用美国国家航空航天局(National Aeronautics and Space Administration, NASA)艾姆斯研究中心的锂电池测试数据来分析不同温度以及充放电循环对电池容量的影响。在磷酸铁锂电池的测试中以25℃时的电池容量为基准分析在不同温度下的电池相对容量百分比(relative capacity of battery,CR%)，如附录图A2所示。在高温环境下，CR%略有提高，但提升幅度不明显，在40℃时CR%为106%，当环境温度大于55℃时CR%上升趋势转为下降。在低温环境中，CR%相对于基准容量下降幅度明显，当温度到达-20℃时CR%仅有43%。为了量化充电负载模拟过程中温度对电池容量的影响，采用多项式函数模型拟合温度和CR%之间的关系，如式(7)所示。

式中：T为环境温度(℃)；η0、η1、η2、η3为函数模型拟合系数；CR为电池相对容量百分数。

2.2 车载空调启停能耗模型

车载空调系统(包括制冷和制热)作为电动汽车主要耗能电器直接影响了电动汽车充电需求以及续航里程[18]。在不同的环境温度和湿度等天气条件下空调系统的启停和能耗值也会有所差别，根据实验数据分析不同温度T下车载空调耗能，并通过车载空调开启时的能耗数据拟合得到空调能耗和空调使用率随温度变化如图1所示。

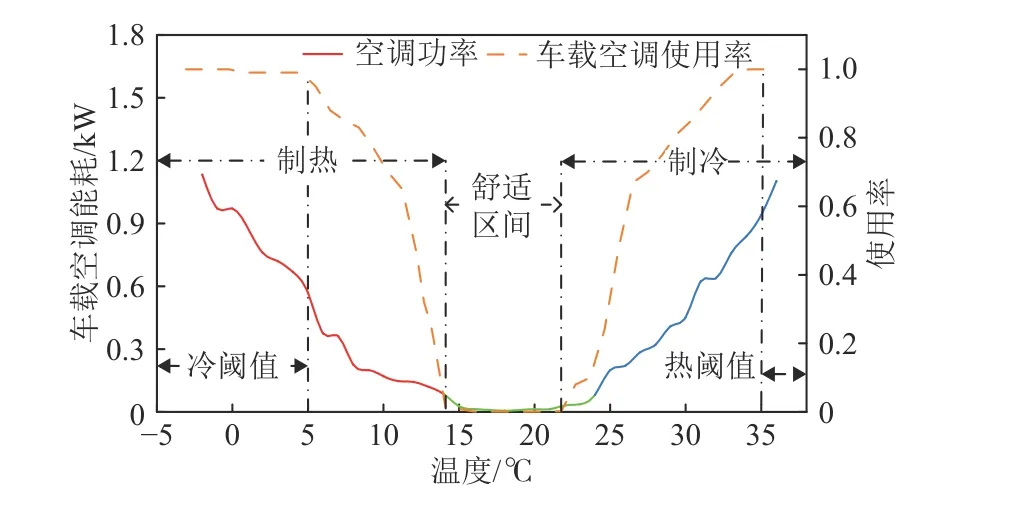
图1 不同温度下车载空调能耗及使用率Fig.1 Energy consumption and usage rate of EV airconditioner under different temperatures

在文献[8]的基础上，对空调开启决策模型进行改进，通过对车载空调使用率曲线分析建立相应的空调开启决策模型，根据车载空调使用率曲线进行正态分布拟合，并设定冷阈值Tc、热阈值Th以及舒适温度区间，介于阈值与舒适温度之间的分段曲线根据MATLAB中的cftool工具箱进行正态分布拟合获得相应的拟合参数得到相应的空调启动正态分布函数，如式：

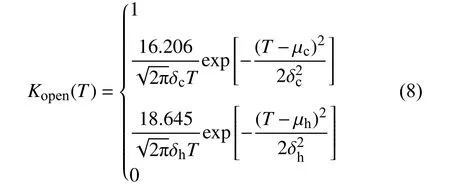
式中：Kopen(T)为温度T下空调开启概率；μc、δc为制热启动参数的均值与方差；μh、δh为制冷启动参数的均值与方差，当温度低于冷阈值Tc或者大于热阈值Th时用户空调开启概率为1；当温度在舒适温度区间内，开启空调的概率为0。参数值设定如表2所示。

表2 车载空调开启概率拟合参数Table 2 Fitted parameters of EV air condition starting-up probability

为了量化充电负荷模拟中日内温度变化对空调能耗的影响，可采用分段多项式模型拟合温度与空调功率之间的关系，如式(9)所示。

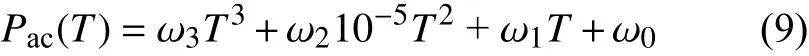
式中：Pac为空调功率；ω0、ω1、ω2和ω3为函数拟合系数。

2.3 基于交通路况的里程能耗模型

电动汽车在正常行驶过程中单位里程能耗主要受不同道路等级以及交通路况的影响最显著。为了消除了各路网络车速与感觉不一致的问题，充分吸取了人们对不同等级道路拥堵的容忍感受，引入交通拥堵指数(transport performance index, TPI)用数值方式量化描述道路交通运行状态，提高道路交通运行状态表达精度。由于车辆以非经济速度行驶，交通拥堵增加了驾驶持续时间和空调服务时间，降低了驾驶效率，这些将显著影响能源消耗和充电需求，引入行驶时长修正系数ζt调整在不同交通路况下的驾驶时长[17]。用户在道路选择上优先选取道路畅通的路段，对于交通拥堵指数值越高的路段，行驶速度越低，行驶时间越长，用户选择意愿越低，具体如表3所示。

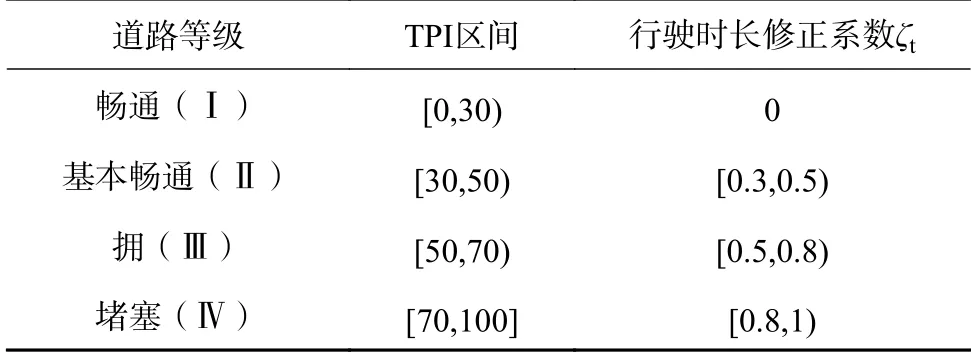
表3 道路交通拥堵指数等级划分Table3 Grading of road traffic congestion index

将道路分为快速路、主干道和次干道3个等级，通过实时交通路况调查获取整体交通路况随时间变化情况[19]，并根据不同时间段内的TPI选取对应的平均速度代入交通能耗因子模型内，如式(10)所示，不同交通拥堵程度下各等级道路行车速度的选取如表4所示。

表4 不同交通拥堵程度下各等级道路行车速度Table4 Running speeds of each level roadsunder different traffic congestion degree

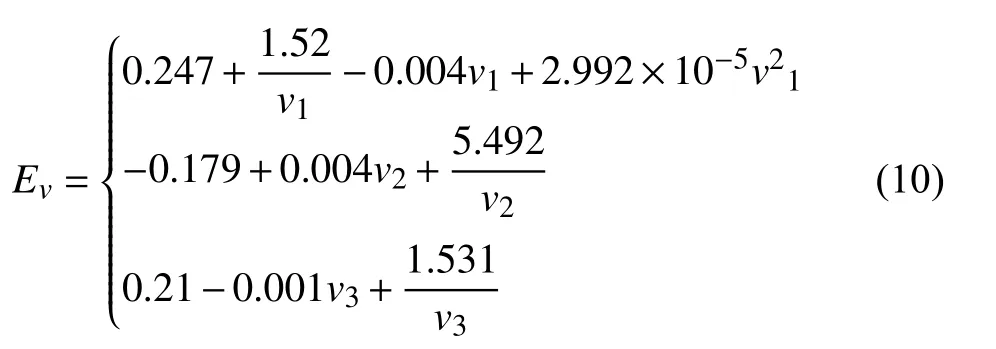
式中：Ev表示电动汽车在不同等级道路中以速度v行驶时产生的单位里程能耗，单位为kW·h/km；v1、v2、v3分为快速路、主干道和次干道3个道路等级下的行车速度，速度取每段道路上的平均行驶速度，单位为km/h。

综上所述，电动汽车在不同环境温度T以及交通路况中的实际耗电量可由电池能耗模型精确计算，如式(11)所示：

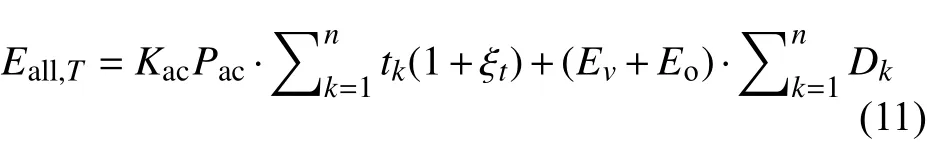
式中：Eall,T为电动汽车在温度T下的总能耗值；Kac为温度T下的空调启停状态，取值为1或者0(表示车在空调开启和关闭状态)；tk、Dk为第k段出行过程中的行驶时长和行驶里程；Eo为电动汽车初始单位里程能耗；ζt为行驶时长修正系数，其取值如表3所示，表示在电动汽车受交通拥堵路况影响，对行驶时间和速度进行修正。

3 基于用户心理的电动汽车充电需求模型

3.1 基于锚定效应的用户充电决策

锚定效应(anchoring effect)，是指个体在不确定情境下进行判断时其最后估计结果向该初始值的方向接近而产生偏差。用户在进行充电决策时，分时电价会成为“锚”而影响用户的充电决策行为，不同的锚值会对用户的充电意愿产生不同影响[20]。由于用户的充电行为受到电网分时电价的调控，通过提高峰值电价、降低谷值电价影响电动汽车充电负荷，达到“削峰填谷”的效果。锚定效应通过定义“高锚”与“低锚”的概念去判断用户对电价的接受程度。其中“高锚”是指用户对电价的期望值要高于实际价格，“低锚”是指用户对电价的预期值要低于其实际价格。在充电决策过程中，不同的“锚”会对用户的充电意愿产生不同的影响，与低锚相比，高锚能产生更高的充电意愿。消费者剩余是愿意支付的最高电价与实际分时电价之间的差额。充电决策过程中用户将实时电价与预期支付电价进行比较，通过对消费者剩余的感知进行充电决策，如图2所示。

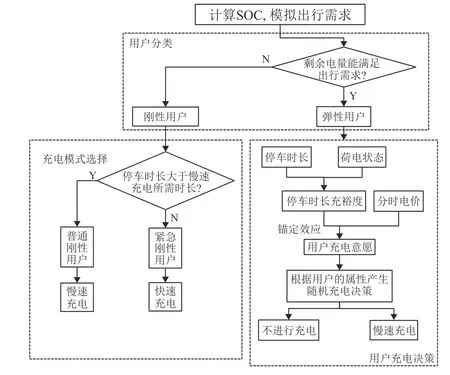
图2 用户充电决策过程Fig.2 User's charging decision process

当EV荷电状态(state of charge,SOC)无法满足下一次出行的电量需求时，用户会根据停车时长进行充电模式选择，对于停车时长充裕的用户定义为普通刚性用户，选择慢充方式进行充电；对于停车时长内慢充无法满足下次出行需求的用户定义为紧急刚性用户，选择快充方式进行充电。当电动汽车的SOC充裕且满足下一次出行的电量需求时，充电决策取决于不同锚值设定时产生的消费者剩余，将愿意支付的最高价格高于实时电价的用户定义为高锚弹性用户，根据消费者剩余充裕度，用户会进行充电行为；将实时电价高于用户电价预期值定义为低锚弹性用户，由于消费者无剩余，则不会进行充电行为。出于对电池寿命的考虑，弹性用户在家充电优先使用慢充方式进行充电。

3.2 充电需求计算

基于不同用户类型、车辆类型的出行特征，在每个路段节点判断电动汽车的进行充电行为，将不同功能区内的充电需求进行叠加，得到电动汽车充电需求的时空分布。具体仿真计算流程如图3所示。

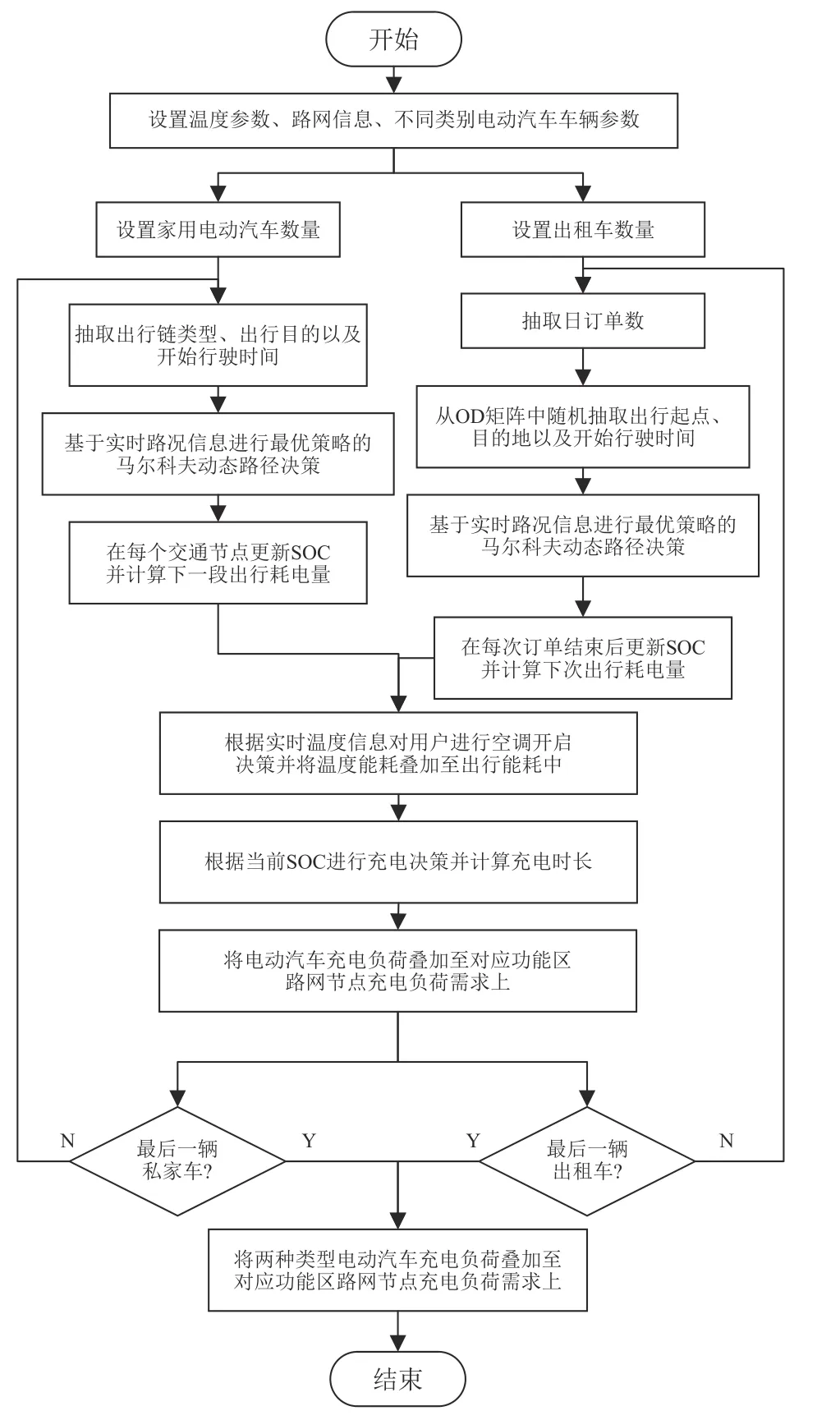
图3 充电需求计算流程Fig.3 Flowchart of calculating charging demand

1）设置温度、交通路况相关参数以及不同类别的电动汽车车辆参数；

2）根据EV充放电循环次数以及环境温度计算并更新电池容量；

3）基于出行链理论模拟家用电动汽车的出行，运用蒙特卡洛法随机抽取出行链类型、时间参数以及出行目的地；根据日订单数量时空分布以及OD概率转移矩阵，运用蒙特卡洛法随机抽取日出行次数以及出行起讫点；

4）通过最优策略的MDP路径决策模型确定行驶路径；在每个出行道路节点，预先计算下一段出行过程产生的耗电量，根据电动汽车的剩余电量是否满足下一段出行的用电需求，对用户的充电决策进行判断；

在宿州市特色农产品销售管理系统功能模块实现之前，需要优化的系统架构，可以为该系统未来的可持续拓展和延伸提供保障。在该销售管理系统技术架构实现过程中，本文以移动端App和服务器端两个部分组成。两个部分构建的基础数据库都是采用的SQLserver数据库。在移动端部分，本销售管理系统基于Windows系统内核，利用谷歌公司的Andorid Studio开发环境构建移动端的框架体系。在服务器部分，基于Windows系统内核，利用模型—控制理论，在JFinal体系下，基于基层通信链路，构建特色农产品销售管理系统的服务器。

5）将各个区域的充电需求按照电动汽车数量进行累加，得到总的电动汽车充电需求时空分布。

4 算例分析

4.1 参数设定

设定各类型电动汽车数量以及不同类型家用电动汽车和出租车的占例，如表5所示。电动汽车开始出行时刻的SOC服从正态分布N(0.8,0.12)，充电站的充电模式选择快充和慢充两种充电方式，根据国家推广的电动汽车充电桩类型以及位置分布，设定不同功能区的充电模式以及充电功率，各区域充电模式与充电功率如表6所示。家用电动汽车出行链类型以及占比设定如表7所示，以成都三环区域内的路网为参照形成电动汽车出行路网模型。

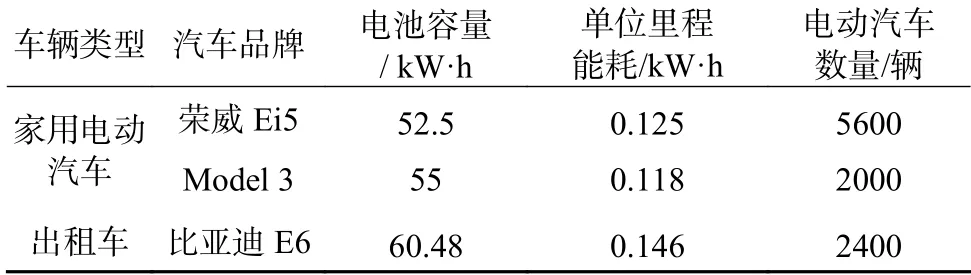
表5 各类型电动汽车数量及参数Table 5 Number and parametersof each typeof EV

表6 各区域充电模式与充电功率Table 6 Charging modes and charging power in each region

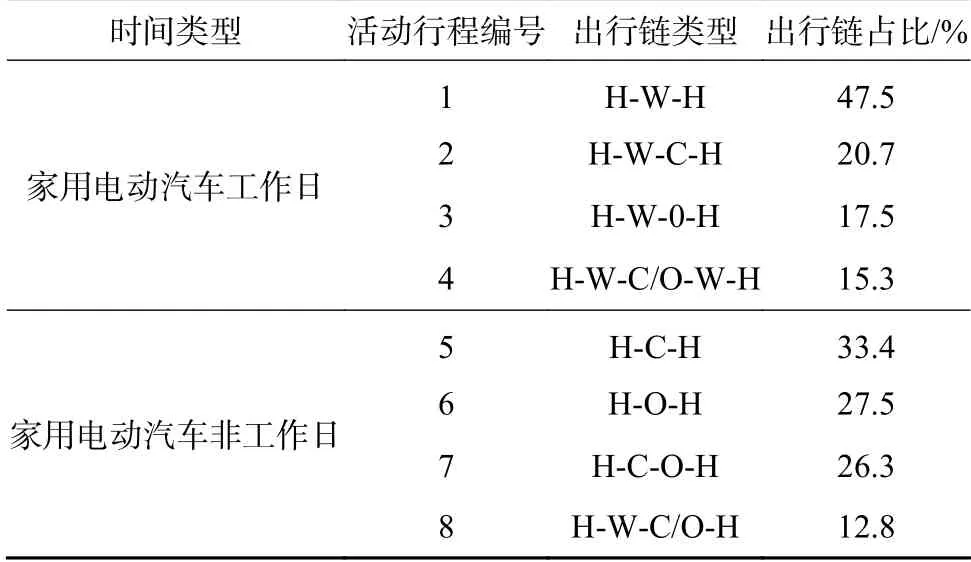
表7 家用电动汽车出行链出行活动类型及占比Table7 Travel activity typeof household EV trip chain and proportion

4.2 仿真结果

1）电动汽车充电负荷时空分布。

在不同功能区内电动汽车充电负荷特性有一定差异性，如图4所示。以工作日充电负荷为例，充电负荷白天主要集中在工作区，负荷占比高，充电负荷高峰发生在10:27，负荷峰值为8.91 MW；夜间则分布在住宅区，在16:00—20:00时段充电负荷较为集中，负荷峰值为4.02 MW。商业区充电负荷在工作日充电负荷整体偏小，负荷高峰时段发生在12:00—18:00，负荷峰值为0.23 MW。

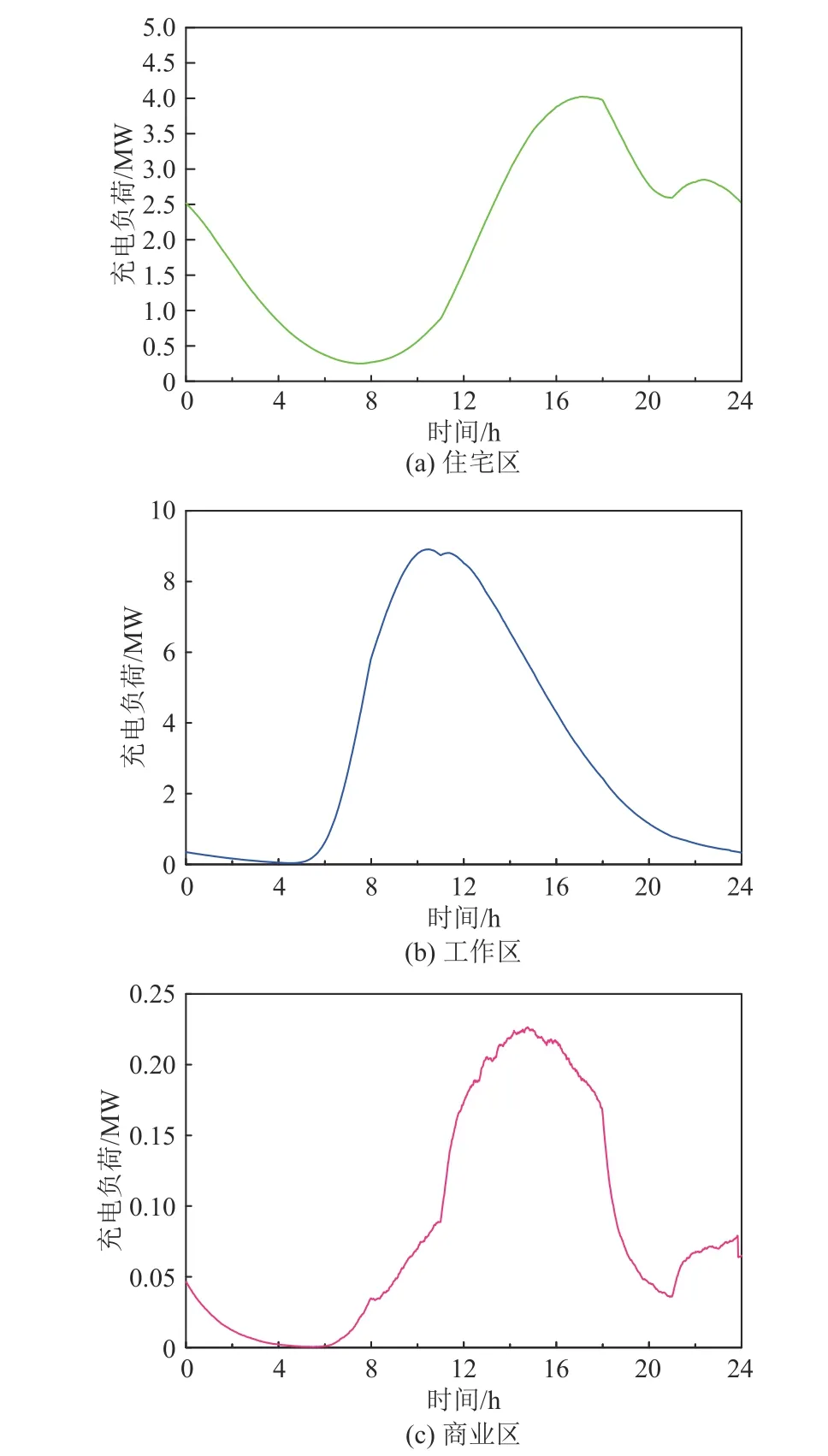
图4 各区域电动汽车充电负荷时空分布Fig.4 Spatial and temporal distribution of EV charging load in each region

比较工作日与双休日总充电负荷曲线，如图5所示。工作日总充电负荷从5:18开始逐渐增大，在12:21达到充电负荷高峰，峰值为10.46 MW。相比于工作日，双休日充电负荷更加集中，负荷高峰推迟至14:16，负荷峰值为15.61 MW，负荷峰值相较于工作日增长了49.25%。由于工作日出行高峰发生在上下班时段，而在双休日出行高峰集中在12:00—17:00，因此充电负荷增加时间段不同。用户在双休日出行活动更加频繁且出行集中在出行高峰，同时在双休日租出车订单数量增多，日间出行量增大，充电需求整体增多。

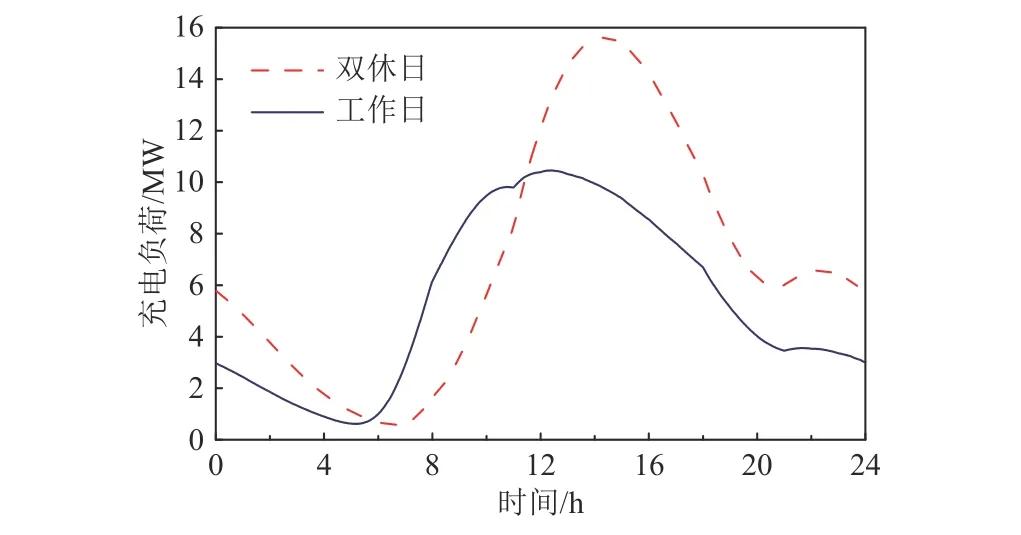
图5 各场景电动汽车总充电负荷时间分布Fig.5 Total charging load time distribution of EV in each scenario

2）动态能耗模型对充电负荷的影响。

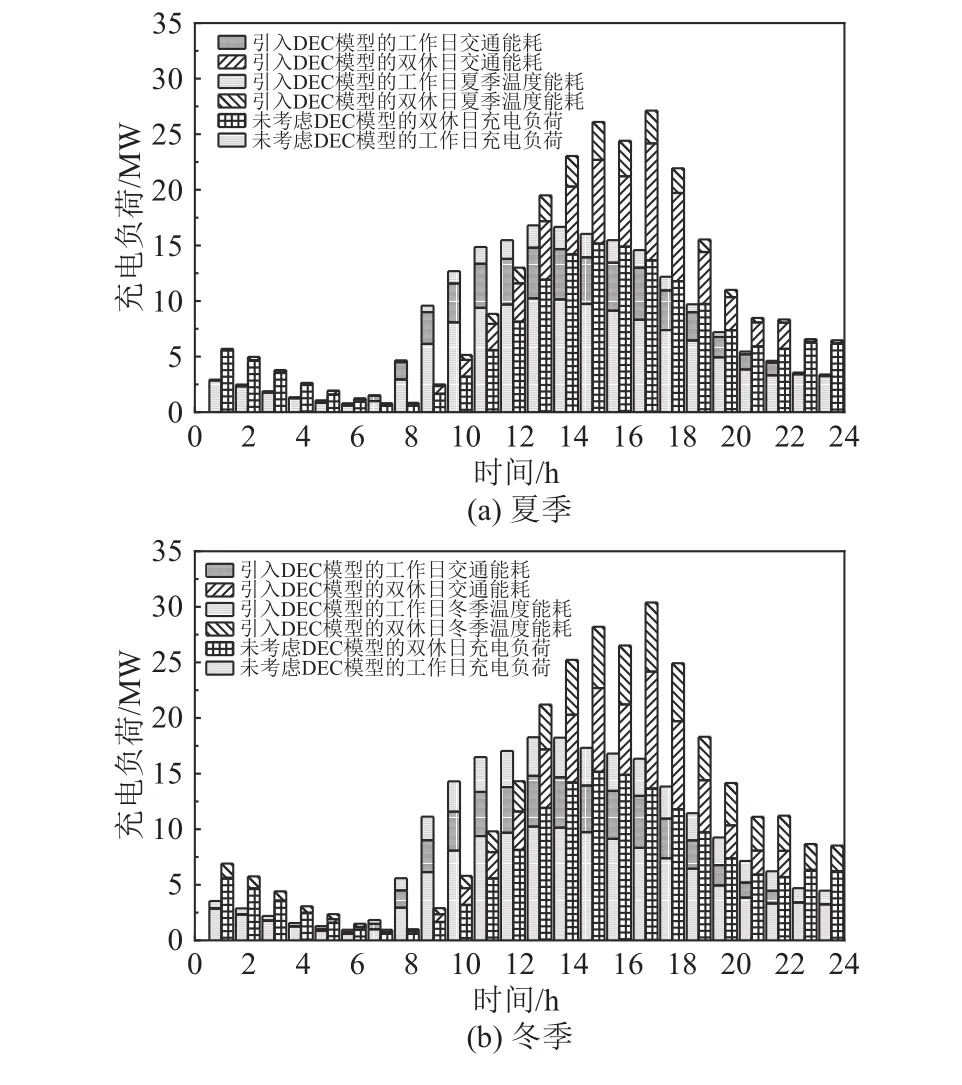
图6 基于DEC模型的电动汽车充电负荷Fig.6 EV charging load based on DEC model

结合图6与表8可知，在夏季高温或者冬季低温的环境中，路况与温度对电动汽车充电负荷影响显著。以夏季工作日为例，夏季8:00～10:00为出行高峰时段，交通拥堵指数高，电动汽车在行驶过程中里程能耗增加，电动汽车充电需求开始激增；在夜间交通畅通时段，由交通路况引起的能耗明显偏低。引入DEC模型后，在出行高峰期受交通路况影响产生的额外充电负荷占总充电负荷的28.17%。随着时间推移，夏季温度逐渐升高，在高温时段10:00—15:00，由温度引起的能耗值持续上升，最大增幅为13.09%。针对不同季节分析，由于在冬季低温环境下车载空调的使用率高于夏季，而且在低温环境中电池容量降低，充电次数更加频繁，导致冬季充电负荷的峰值及充电需求总量高于夏季，冬季温度引起的日充电负荷占总充电负荷的21.17%。仿真结果验证了DEC模型的有效性，符合实际情况。

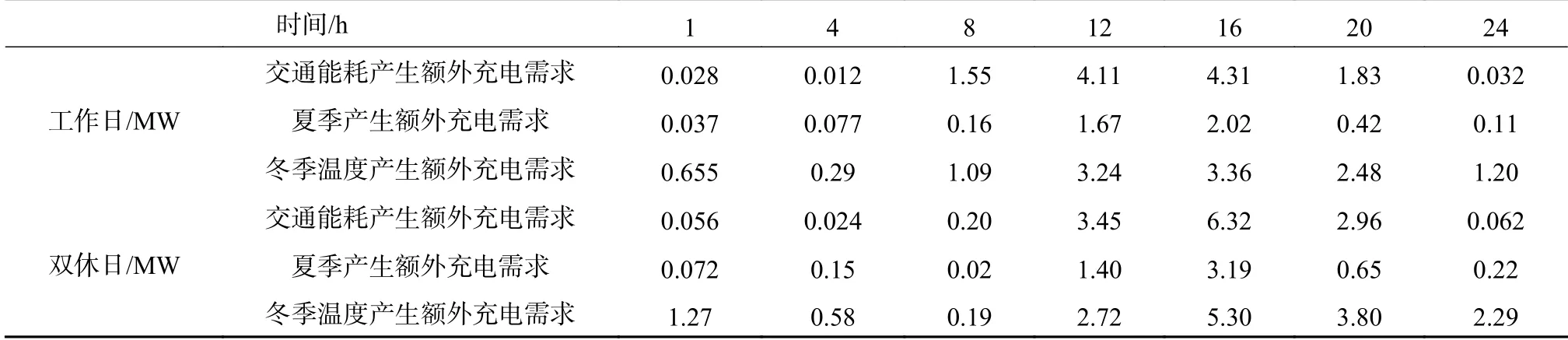
表8 引入DEC模型的电动汽车充电负荷变化Table 8 Change of EV charging load under DEC model led in

5 结论

电动汽车充电负荷时空分布受多源客观因素与用户心理影响，故提出一种基于动态能耗模型与用户心理的电动汽车充电负荷预测模型方法，并以成都三环内的实际路网交通为依托对电动汽车充电负荷进行了时空分布预测，仿真结果表明：

1）充电区域、充电偏好以及时间场景类型会影响充电负荷曲线的大小、峰值时间和曲线形状。不同区域的电动汽车充电负荷在时间分布上存在明显的差异性。工作日充电负荷曲线相对平缓，而双休日充电负荷更加集中，负荷峰值相较于工作日增长了49.25%。

2）考虑道路等级、路况交通、车速以及气温等外界客观因素的影响与未考虑情况下的电动汽车充电负荷曲线在特性和幅值上有很大差异。峰值负荷之差高达21.17%，且出现最大峰值时间会发生偏移现象。受温度影响，冬季电池容量明显缩小，冬季情况下温度过低造成电池容量衰减对充电负荷的影响更大，车载空调开启更加频繁，导致负荷峰值持续升高且峰值持续时间增加，冬季充电负荷充电需求总量远高于夏季。

仿真结果验证了模型的有效性和方法的可靠性，动态能耗模型能够准确获取在不同环境状态下电动汽车的实际能耗，提高负荷预测结果的精度，为配电网的布局配置提供的合理规划依据。

本文假设在各个路网节点均有充电且充电站的容量足够大，因此忽略了汽车充电的排队时间以及电动汽车在充电时充电站的选择过程，需要将实际中充电站分布情况做进一步分析。

（本刊附录请见网络版，印刷版略）