电力市场环境下考虑可再生能源保障性消纳的电价风险评估
何洁,金骆松,赵雯,黄恒孜,李思颖,桑茂盛,丁一
(1.浙江电力交易中心有限公司,浙江省杭州市 310016;2.浙江大学电气工程学院,浙江省杭州市 310027)
0 引言
自21世纪以来,全球气候与环境条件对人类社会提出了巨大考验,低碳化成为世界能源产业发展的必然趋势[1-2]。当前,我国也正处于能源转型的关键时期,习近平总书记关于“CO2排放力争于2030年前达到峰值,努力争取2060年前实现碳中和”的庄严承诺为新时代我国能源低碳转型指明了方向[3]。低碳化趋势和能源转型目标的提出将促使高比例可再生能源接入电网,2020年风电、光伏等可再生能源发电量超过2.2万亿kWh,占全部发电量比重接近30%,预计到2025年可再生能源发电装机占我国发电总装机50%以上[4]。未来,以风电、光伏为主的可再生能源将逐渐成为我国主要的能源供应形式[5]。
与此同时,2015年3月《中共中央国务院关于进一步深化电力体制改革的若干意见》(中发[2015]9号文)发布以来[6],我国新一轮电力体制改革开展迅猛。在9号文及相关配套文件的指导下,全国各省结合政策要求和自身实际情况稳步推进电力市场化建设,广东、浙江等8个试点省份已建立省级电力市场,电力市场化改革成效显著[7]。随着电力市场建设的持续推进,市场在资源优化配置中的作用愈加明显,通过市场化机制实现可再生能源优先或保障性消纳,是我国电力市场建设的重要任务[8-9]。然而,以风电、光伏为代表的可再生能源发电在降低系统发电成本、减少碳排放的同时,其出力不确定性和间歇性的特点也可能会给电力市场运营带来不可忽视的影响。
电力市场环境下的电价机制与传统计划体制下的电价机制存在很大差异,国际上采用的电价模型主要包括节点、区域和系统电价,其中美国PJM、ERCOT等电力市场以及我国试点省份大多采用节点边际电价,因为其能够反映电力供需和网络阻塞信号,同时该模型也是其他电价模型的基础[10]。为了保证可再生能源优先消纳,在多数电力市场出清模型中,将可再生能源预测出力作为边界条件进行出清计算。以广东电力现货市场规则为例[11],为了保障可再生能源消纳,在实时电力市场对日前可再生能源出力边界进行调整。但是,可再生能源出力边界条件的变化可能会使实时电力市场出清电价发生变化,导致电价波动剧烈[12]。因此,随着可再生能源占比的逐渐增大,亟需重视由可再生能源出力不确定性造成的电力市场出清电价风险[13]。
当前,针对电力市场环境下的电价进行风险分析的研究工作已经开展较多。文献[14]研究了考虑随机故障影响的电价风险分析模型,并提出了期望节点电价等量化评估指标;文献[15]提出了考虑应急备用的节点电价和节点可靠性分析方法,分别用于评估节点电价风险和市场运行可靠性;文献[16-17]分析了可再生能源对市场运行效益的影响,但是所考虑的可再生能源发电规模较小,且被视为用户侧负荷进行建模;文献[13]提出了概率边际电价的概念,分析了风电不确定性引起的实时市场价格波动风险并提出了价格管理机制;文献[18-19]基于数据驱动方法对风电渗透和电力市场价格波动进行了关联性分析,结果表明高比例可再生能源接入电网更容易导致电价飙升。上述文献对电力市场环境下的电价波动以及电力系统可靠性问题进行了深入研究,而鲜有兼顾电力市场整体和节点层面的高比例可再生能源的参与对出清电价造成风险的分析,目前也尚无有效的量化评估方法和指标体系。作者对可再生能源引起的系统电价风险在国际会议ICNERA2021上进行了初步探讨[20],但是尚未从节点层面提出详细的电价风险分析方法,难以有效辨识高电价风险的区域或节点,所提模型对我国各试点省份指导作用有限。
针对上述研究的不足,本文提出考虑可再生能源参与的电价风险评估方法,针对电力市场环境下可再生能源保障性消纳引发的电价风险进行量化分析,旨在促进可再生能源消纳的同时,也重点关注由此造成的电价风险,为可再生能源参与电力市场提供一定的理论指导。
1 可再生能源出力场景缩减方法
可再生能源的不确定性主要是指出力的预测偏差[21],因此,本文采用多场景技术描述风电、光伏可再生能源出力的不确定性,主要算法步骤如下:
1)采用预测箱对风电、光伏历史发电数据进行统计,根据每个预测箱的历史实际数据分布情况,拟合得到累积经验分布函数。
2)按照文献[22],通过递归估计协方差矩阵ΣT,描述可再生能源出力的时间相关性。递归方程如式(1)所示
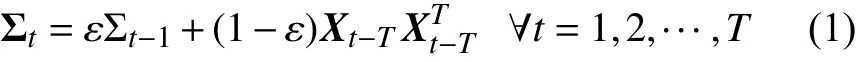
式中:Σt和Σt-1分 别表示时刻t和 t-1的协方差矩阵,为T×T 阶矩阵;ε表 示遗忘因子; Xt-T表示可再生能源在历史时刻t-T的实际出力(经累积经验分布函数转化为服从正态分布的样本[21]),为T维向量;T为预测周期。
3)基于估计的协方差矩阵ΣT,采用蒙特卡洛模拟法进行随机采样,生成服从标准正态分布N(0,ΣT)的T维随机数。
4)根据累积正态分布函数,得到每个随机数对应的累积概率。
5)基于累积经验分布逆函数[23],得到对应累积概率的实际可能出力,即出力场景。
6)采用基数约束子模块化(cardinality constrained sub-modularity,CCS)的场景缩减法[24]对大量场景进行削减,使得最终保留的场景子集与未削减前的场景集合之间的概率距离最小[25],如式(2)所示。

式中:Pi和Pj表示可再生能源在场景 i和场景 j下输出功率的时间序列;I 和J分别表示被削减的场景子集和最终保留的场景子集;λ表示相似性控制参数。
基于上述可再生能源出力场景生成算法,可以得到有限数量的具有较大概率值的典型场景集合,以逼近原始场景集合。
2 电价风险评估
2.1 市场出清与节点电价
首先,建立考虑可再生能源保障性消纳的电力市场出清优化模型,目标函数为总发电成本费用与弃风弃光以及失负荷惩罚费用之和最小[26]

值得说明的是,为了保障可再生能源的消纳,目标函数公式(3)中弃风、弃光惩罚价格应设为远大于发电机组报价值,只有当电网由于物理运行约束不满足导致全额消纳条件下出清模型无解时,才会出现弃风、弃光情况。模型满足以下约束条件[20]。
1)节点功率平衡方程:各节点的净注入有功/无功功率等于净流出有功/无功功率。
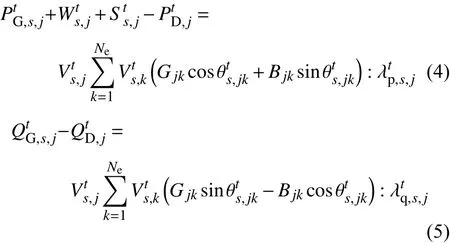
在电力市场实际运行中,一般采用直流潮流法对潮流方程进行简化[9],本文主要从理论层面研究交流潮流环境下的出清电价风险,但所提模型和方法同样也适应于直流潮流环境。
2)常规机组出力限制:各机组的有功/无功中标出力不能超过其出力上限和下限,各机组在相邻时段的出力变化量不能超过其上下爬坡限制。
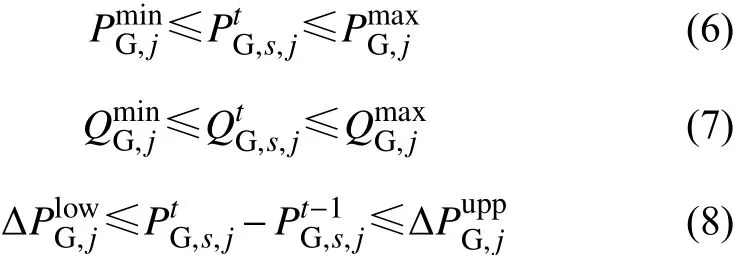
式中:PmG,inj和PmG,ajx分别表示节点 j上发电机组的有功出力下限和上限;QmG,inj和QmG,ajx分别表示节点j上发电机组的无功出力下限和上限;ΔPlGo,wj和ΔPuGp,pj分别表示节点j上发电机组有功出力的下爬坡限制和上爬坡限制。
3)风电、光伏出力限制。风电、光伏机组的有功出力不能超过其出力预测值。
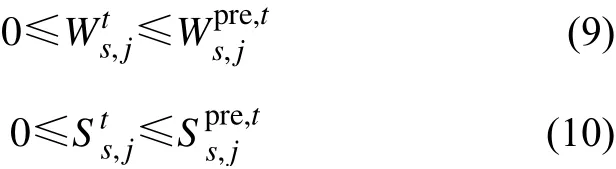
4)线路传输容量限制。各输电线路、区域间联络线的潮流不能超过其传输容量。

式中:Fts,l为 线路l在 场景s流过的潮流; Flmax表示线路l 的最大传输容量。

式中: fst,rr′为区域r和r′间联络线在场景s流过的潮流; frmr′ax分别表示线路l、区域r和r′间联络线
的最大传输容量。
5)节点电压限制。各节点的电压幅值不能超过其上下限。
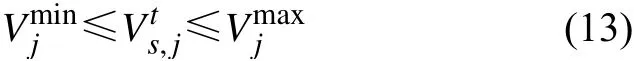
式中:Vmjin和Vmjax分别表示节点j的电压幅值下限和上限。
6)负荷削减量限制。各负荷节点的负荷削减量不能超过其初始负荷。

上述电力市场出清模型(式(3)-(14))是一个复杂的非线性优化问题,内点法在求解非线性优化问题方面具备收敛性强、计算速度快等优点[27-28],因此,可以采用内点法对上述模型进行求解,得到电力市场出清结果。
基于上述电力市场出清模型,得到拉格朗日函数Ls,可以计算节点有功电价ρtp,s,j、节点无功电价ρtp,s,j[14]:

进一步计算系统平均有功电价ρtp,s和系统平均无功电价ρtq,s:

2.2 电价风险评估指标体系
2.1 节可以计算得到各场景s下的节点有功电价ρtp,s,j和节点无功电价ρtq,s,j、系统平均有功电价ρtp,s和系统平均无功电价ρtq,s。由于可再生能源出力具有波动性和间歇性,某些场景下某些时段电价可能会很高,或者不同场景下电价波动较大,都可能会造成电价风险。因此,本文建立电价风险评估体系,包括:节点电价风险指标体系和系统电价风险指标体系,分别评估节点电价和系统电价的风险。另外,本文主要研究有功电价,无特别说明,电价风险指标均指有功电价。
1)节点电价风险指标体系。

式中:Ns为通过场景生成算法最终保留的场景数;ps表 示场景s发生的概率。
节点电价标准差σp,j[14]:用于评估各节点电价在所有可能发生场景下的波动情况。
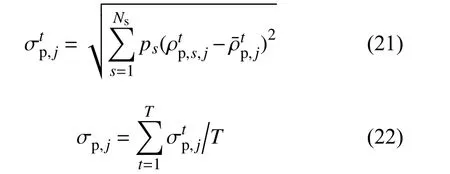
节点尖峰电价概率ζp,j:用于评估各节点电价在所有可能发生场景下出现较高值的可能性。

式中:ρcpap为设定的电价阈值; 1(ρtp,s>ρcpap)为符号函数,当随机事件ρtp,s>ρcpap发生时,函数取值为1,否则为0。
2)分区电价风险指标体系。
分区尖峰电价概率ζp,r:用于评估区域内平均电价在所有可能发生的场景下出现较高值的可能性。

式中:Ωr表示区域r内的节点集合。
3)系统电价风险指标体系。
期望系统电价ρtp:用于评估系统平均电价在所有可能发生场景下的期望水平。

系统电价标准差σtp:用于评估系统平均电价在所有可能发生场景下的波动情况。
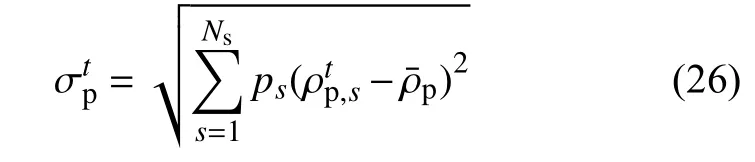
系统尖峰电价概率ζp:用于评估系统平均电价在所有可能发生场景下出现较高值的可能性。
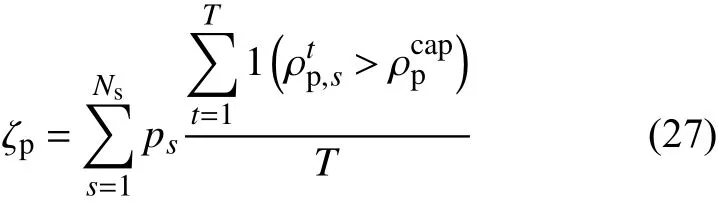
3 算例分析
3.1 算例系统
为了验证本文所提出的电价风险评估方法的有效性,采用改进的IEEE30节点系统作为算例系统进行分析。该系统包含6台常规机组、30个节点、41条线路。负荷数据、机组参数以及报价信息参考文献[29],线路容量参数参照文献[30]。在第20节点和第28节点处分别接入一个风电厂和一个光伏电站,发电容量依据不同的分析环境进行设定。考虑到风电、光伏的边际发电成本很小,报价参数按照最低来设置。风电和光伏历史数据参照文献[21],并折算为本算例数量级。另外,为了保障可再生能源的消纳,且尽量避免系统失负荷,将弃风弃光惩罚价格和失负荷惩罚价格设为远大于发电机组报价的数,其中,所有节点的弃风、弃光惩罚价格统一设为1000元/MW·h,失负荷惩罚价格统一设为5000元/MW·h。
3.2 不同可再生能源渗透率下电价风险计算结果及比较
为了研究不同可再生能源渗透率对电价风险的影响,本文设定6种分析环境,各分析环境下风电、光伏发电容量设置如表1所示。

表1 不同分析环境下可再生能源机组发电容量Table 1 Generating capacity of renewable energy units under different analysis environments
首先计算各环境下的系统电价风险值。根据风电和光伏历史数据[19],利用第1节提出的可再生能源出力场景生成算法得到最终5个典型场景下的风电、光伏出力及场景概率,出力真实值可根据各环境设定的风电、光伏发电容量折算得到。
以环境0—环境3为例,不同可再生能源渗透率下的期望系统电价、系统电价标准差与系统尖峰电价概率ζp的计算结果分别如图1、图2和图3所示。电价阈值根据可再生能源出力预测值得到的市场出清电价最高值而定。
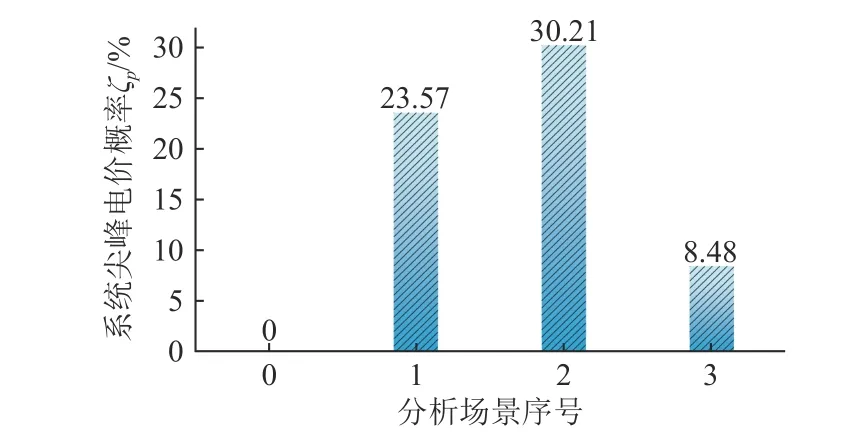
图3 不同可再生能源渗透率下系统尖峰电价概率Fig.3 Probability of system peak price under different renewableenergy penetration
由图1可以看出,可再生能源机组接入电网后,系统整体的电价水平也有所下降,且渗透率越高,电价降低越明显。其中,环境5中的期望电价降低最为明显,这是因为可再生能源相比常规机组发电成本较低,随着渗透率的增大,可再生能源出力也不断增大,而环境5中的可再生能源出力最大,代替高成本机组发电,导致期望系统电价也随之下降。

图1 不同可再生能源渗透率下期望系统电价Fig.1 Expected system price under different renewable energy penetration
由图2可以看出,在不同可再生能源渗透率下,系统电价标准差也存在差异,可再生能源渗透率越高,系统电价标准差越大。比较环境1和环境2,可以看出环境1下的电价标准差更大,表明风电比光伏更容易导致电价的波动性,这是因为在本算例中,风电的预测误差标准差比光伏更大。另外,可以看出在15~22 h时段内,系统电价标准差相对较高,这是因为这段时间内为可再生能源出力的高峰期,电价对可再生能源出力的波动性较为敏感。
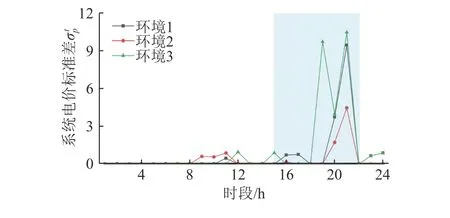
图2 不同可再生能源渗透率下系统电价标准差Fig.2 Standard deviation of system price under different renewableenergy penetration
与系统电价标准差不同,系统尖峰电价概率与可再生能源渗透率的关系恰好相反。由图3可以看出,环境2下的系统尖峰电价概率最高,达到了30.21%,随着可再生能源渗透率的提高,环境3下系统尖峰电价概率有所降低。这是因为可再生能源发电占比的增大,导致电价水平整体下降,因此出现尖峰电价的概率也相应变小。进一步将系统中前7个节点设为区域1,其余节点设为区域2,计算可知2个区域的分区尖峰电价概率分别为21.77%、32.78%,表明区域2存在更高的电价风险。
以上重点对系统和区域层面的电价风险指标进行了分析,下面进一步从节点层面研究可再生能源对电价风险的影响,计算各环境下的节点电价风险指标,不同可再生能源渗透率下的期望节点电价和节点电价标准差分别如图4-6所示。
由图4可以看出,不同环境下各节点的期望电价水平不同,表明系统存在网络阻塞情况,导致不同节点之间的电价存在差异。另外,随着可再生能源渗透率的提高,各节点的期望电价水平有所下降。由图6可以看出,随着可再生能源渗透率的提高,节点出现尖峰电价的概率也有所下降。另外,由图4可以看出,18-20、25-30节点受到可再生能源的影响最明显,电价降低程度最直观。由图5也可以看出,这些节点的电价标准差也远大于其他节点,对可再生能源渗透率的变化也很敏感。根据系统拓扑可知,这些节点处于可再生能源接入点及其附近的位置,表明越靠近可再生能源接入点,节点电价风险可能更高。因此,随着可再生能源发电比例的提高,应重点关注可再生能源接入点附近的节点电价,避免电价剧烈波动。

图4 不同可再生能源渗透率下期望节点电价Fig.4 Expected nodal price under different renewable energy penetration

图5 不同可再生能源渗透率下节点电价标准差Fig.5 Standard deviation of nodal price under different renewable energy penetration

图6 不同可再生能源渗透率下节点尖峰电价概率Fig.6 Probability of system peak price under different renewableenergy penetration
综上所述,随着可再生能源渗透率的提高,可以在一定程度上降低系统和节点的期望电价水平、以及出现尖峰电价的概率,但是可能会增大电价波动程度,对于可再生能源出力高峰时段,系统电价波动较为明显;在靠近可再生能源接入点附近的节点,电价波动程度较为明显。
3.3 不同预测偏差下电价风险计算结果及比较
为了研究不同可再生能源出力预测偏差对电价风险的影响,在3.2节中环境3(风电、光伏发电容量各为50 MW)的基础上,将可再生能源出力预测偏差标准差分别增大5%和10%,计算得到系统电价风险和节点电价风险指标如图7-11和表2所示。

图7 不同预测误差下期望系统电价Fig.7 Expected system price under different forecasting deviations
根据图7-10可以看出,随着可再生能源出力预测偏差的不断增大,期望系统电价和期望节点电价也略微增大,但是增幅不明显,而系统电价标准差在负荷高峰时段增长较大,大多数节点的电价标准差也明显增大。与此同时,根据表2和图11可知,可再生能源出力预测偏差增大也会提高系统尖峰电价概率和节点尖峰电价概率,这是因为由可再生能源出力不足造成的功率缺额由高价机组弥补,导致电价飙升。综上所述,可再生能源出力预测偏差对电价风险的影响主要体现在电价波动程度上,对电价的期望水平影响较小。随着预测误差精度的降低,虽然电价整体的期望水平不会明显变化,但是可能会造成电价波动更加剧烈,增大电价飙升可能性,带来电价风险。因此,提高对可再生能源出力预测的精度,有利于稳定电价水平,降低电价风险。

表2 系统尖峰电价概率Table2 Probability of system peak price
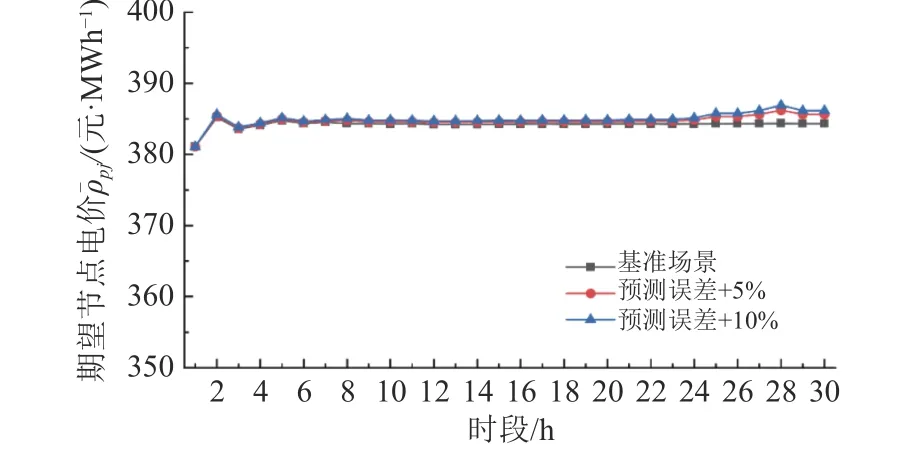
图8 不同预测误差下期望节点电价Fig.8 Expected nodal price under different forecasting deviations

图9 不同预测误差下节点电价标准差Fig.9 Nodal price standard deviation under different forecasting deviations

图10 不同预测误差下节点尖峰电价概率Fig.10 Probability of system peak price under different forecasting deviations
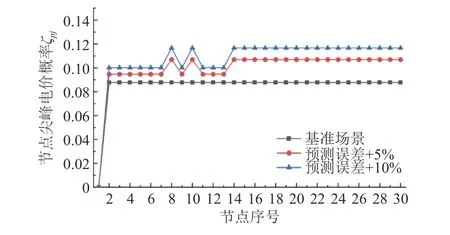
图11 不同预测误差下系统电价标准差Fig.11 System price standard deviation under different forecasting deviations
4 结论
本文所提出的电价风险评估方法可以量化系统整体的电价风险,得到各时段电价的期望水平、波动情况及出现较高值的可能性;同时,也可以从节点层面量化评估各节点的电价风险指标,识别出对可再生能源不确定性较为敏感的关键节点。在促进可再生能源消纳的同时,也要关注由此造成的电价风险,通过提高可再生能源出力预测精度等措施,有效减小出力的不确定性,降低电价风险。
致谢
本文由浙江电力交易中心有限公司科技项目(浙江电力市场大数据分析体系构建研究,SGZJDJ00JYJS2000011)资助,谨此深表感谢。

