基于合作博弈模型的新能源参与电力交易的调控策略

田海青，郭金辉，周瑜，苑芸芸，赵得玮，杨智，刘敦楠，王玲湘

（1.青海电力交易中心有限公司,青海省西宁市 810000；2.华北电力大学经济与管理学院,北京市昌平区 102206）

0 引言

2022年3月22日国家发改委、国家能源局发布《“十四五”现代能源体系规划》，规划十分重视新型电力系统中新能源发展的重要性，在2060年实现碳中和的目标中，风电和太阳能等新能源发电将成为电力系统电能供应主体。新能源具有运营成本低、绿色清洁等优点[1-3]，但同时也具有较高的初始投资、较大的出力波动性、不稳定性等缺点，使得新能源并网过程中存在供需不平衡、电力通道堵塞、电力辅助服务成本过高等问题[4-6]。高占比的新能源并网是实现我国“碳达峰、碳中和”目标的重要途径，但同时也对新型电力系统中新能源的并网和消纳提出了新的挑战。

国内外许多学者针对新能源并网过程中的出力波动性较大、供需不匹配等物理问题展开了研究，目前的主要解决方案可分为两类：一是通过建立配套设施或者提供配套服务以中和新能源的出力波动，实现新能源的并网消纳[7-9]。例如，文献[10]通过储能在源–网侧的优化配置实现新能源的并网消纳，但是要达到较好的新能源协调调度效果，需要有较高的投资建设成本和储能利用效率；文献[11]则提出通过辅助服务市场实现高比例新能源的消纳，但是各类型市场主体之间的杠杆效益平衡，特别是在现阶段中长期发用双侧解耦的条件下的效益分配关系需要进一步梳理。二是通过源网荷储之间的协调互补以平抑新能源的负荷波动，促进新能源的并网消纳[12-14]。文献[15]考虑电力系统中的弃风现象，通过对燃煤电厂进行改造有效消纳了风力弃电节约了生产成本；文献[16]则考虑到我国“三北”地区的弃风问题，通过对柔性负荷进行电能替代改造有效提高了风电对电网渗透率提升了电网的安全稳定运行能力。可见，通过源网荷储互动能够有效提升新能源的并网能力，但是现有研究未充分考虑到电力市场中的主体效益问题和合作方效益分配问题。因此，本文主要考虑基于源网荷储互动的新能源消纳策略，将其划分为基于多能互补的新能源消纳策略和基于源荷互动的新能源消纳策略，并结合电力市场的发展情况做充分的讨论。

考虑到中长期市场和现货市场中新能源的分时段交易和考核各类型资源在与新能源进行协调调度的同时应充分考虑电力市场的履约情况进行设计[17-18]，因此应充分考虑分时段电力耦合需求进行优化调控模型设计。目前针对新能源消纳问题主要是通过建立条件约束模型进行优化求解，一些研究考虑到不同主体之间的关系设计有主从博弈模型、合作博弈模型、非合作博弈模型等。例如，文献[19]通过设计主从博弈模型有效提升配电网的新能源消纳能力并减少了用户成本；文献[20]通过设计常规能源与新能源的合作博弈模型以置换发电权有效缓解了西北地区的弃风弃光现象。在多类型市场主体之间具备协商关系并进行了充分的信息共享时，采用合作博弈模型更符合实际情况且能够获得更高的联盟效益[21-23]。因此本文考虑新能源与其他市场主体之间的互动关系，以最大化综合效益为目标，构建基于合作博弈模型的新能源消纳策略。

本文基于高占比新能源并网的新型电力系统建设需求，结合电力市场背景下新能源厂商、火电厂商和需求侧可调节用户的物理调控能力和市场效益提升目标，首先分析了新能源参与电力市场交易的基本框架，并分析了3种类型的市场主体参与电力市场的电力能源流动和经济效益流动情况；然后考虑新能源厂商和火电厂商的出力耦合性能构建考虑多能互补的合作博弈模型，以提升新能源与火电厂商合作联盟的市场效益并促进新能源消纳；进而考虑新能源厂商和可调节大用户的供需耦合性能构建考虑源荷互动的合作博弈模型，以提升新能源与大用户合作联盟的市场效益并促进新能源消纳；最后通过仿真算例证明了本文所提模型对于新能源并网消纳和电力市场效益提升的有益效果。

1 新能源参与电力市场的交易框架

新能源参与电力市场过程如图1所示交易框架。

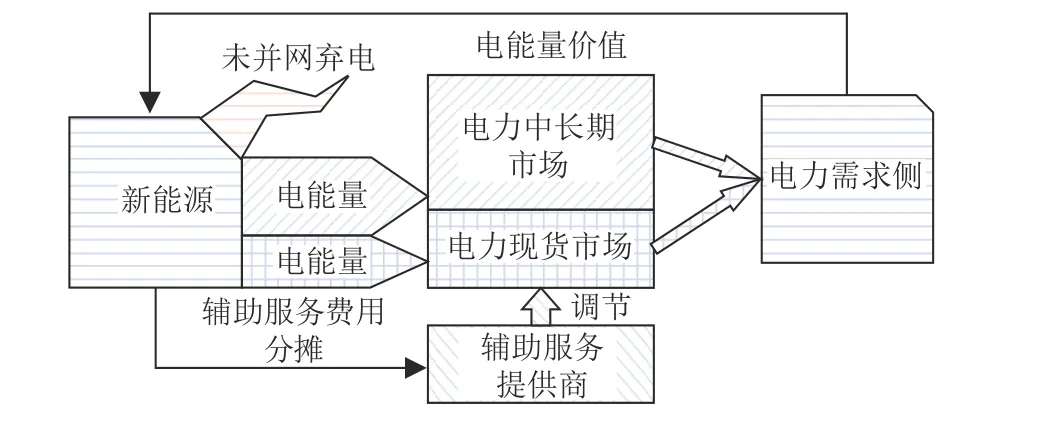
图1 新能源参与电力市场的传统交易框架Fig.1 Traditional transaction framework of new energy participating in electricity market

新能源参与电力市场的过程中，主要是通过参与中长期市场和电力现货市场实现新能源电力的并网交易。该过程中，新能源电力通过电力中长期交易或者现货交易流向电网，最终流向需求侧，然而，新能源固有的波动性和随机性不可避免地给电网带来电力供应波动过大和供需不平衡的问题，为此必须有辅助服务提供商提供上下调服务，调节能力不足时，无法并网消纳的新能源不可避免地产生一部分弃电。该过程中，电力需求侧的电力电量服务费用通过市场流向新能源厂商，新能源厂商则需要向为其提供辅助服务的辅助服务厂商支付一部分辅助服务费用。

为此，考虑到新型电力系统建设过程中不可避免的高比例新能源接入问题，不少地区提出了针对新能源消纳的绿电交易模式。在这种模式下，风光等新能源通过与水火等发电侧能源打捆交易、或者通过与储能、灵活性负荷等需求侧资源互动来降低可再生能源的波动性，在实现高比例新能源的全额消纳，提升了源网荷储多方的市场效益。其能量和效益流动过程如图2所示。

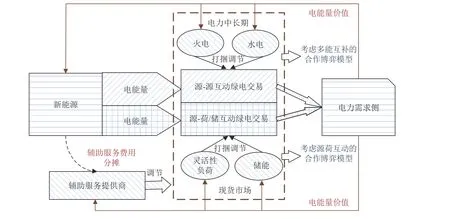
图2 考虑绿电交易的新能源参与电力市场的传统交易框架Fig.2 Traditional transaction framework of new energy participating in electricity market with green electricity transaction considered

该过程中，电能依然是通过中长期和现货市场流向电网进而走向用户，但是可再生能源通过与源侧发电厂商和需求侧灵活性资源之间的互动大幅降低了负荷波动，减少了辅助服务调节压力和弃电规模。该过程中，电力需求侧的电力电量服务费用通过市场流向新能源厂商和其他打捆调节资源，若新能源厂商还有未打捆的波动较大的并网电力则还需支付一部分辅助服务费用。

基于以上分析，可将新能源参与电力市场交易的过程总结以下几点内容：

1）新能源参与电力交易过程的主要难题是新能源出力的不稳定性问题。由于风光等新能源受气候条件的影响较大，在风力资源或者光照资源出现较大波动时，会致使出现较大的出力波动，给电网调控带来困难也提高了输配电成本。

2）供给侧传统能源与新能源的多能互补、需求侧灵活性可调资源与新能源的源荷互动都能在一定程度上缓解新能源波动性大的问题，在该过程中通过构建新能源与传统能源的联盟或者新能源与需求侧可调负荷的联盟形成较为稳定的净出力结构，从而在保障电力供应稳定的同时使得能源供应更加绿色清洁。

3）考虑电力中长期市场和电力现货市场的建设情况，电力联盟在参与电力市场的同时需要考虑分时段价格、偏差考核等多类型关系到电力市场效益的重要问题。在充分考虑市场因素的基础上，设计最优的优化调控方案是本文的主要研究对象。

据此对电动汽车参与电力交易的过程展开优化调控。文章分别针对新能源与供给侧火电资源打捆互动设计考虑多能互补的合作博弈模型；针对新能源与需求侧包括储能在内的可调负荷互动设计考虑源荷互动的合作博弈模型。

2 考虑多能互补的合作博弈模型

2.1 合作博弈基础理论

定义有合作博弈模型通过集体理性行为实现联盟的最大效益，而是否达到联盟的最大效益则通过合作剩余 v({N})、个体的剩余来进行评价v(i)。

稳定的联盟必须创造新的合作剩余，即存在如公式(1)所示的联盟收益创造能力高于个体收益创造能力的基本条件。

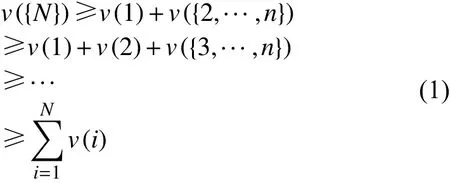
其次，对于联盟内的所有N个成员必须满足每个成员所分得的合作剩余xi高于个体参与时的剩余价值v(i)。即在如公式(2)所示的效益分配关系下，存在有如公式(3)所示的效益提升。

在本文则体现为新能源厂商与传统能源厂商或者需求侧可调负荷之间所形成的联盟，一方面要使得总体效益得到提升，另一方面也需要使各个主体都获得市场效益增量。

2.2 考虑多能互补的合作博弈策略

本节以新能源与火电打捆交易为例研究多能互补的新能源参与电力市场交易策略。在该过程中，通过构建新能源厂商与火电厂商的电力联盟，减少新能源厂商的弃电并增加火电厂商的环保性和经济性，双方都获得了增量收益，满足成立联盟谋取合作剩余的基础条件。

成立发电联盟之后，新能源厂商商定与火电厂商打捆电力交易，在获得新能源预测出力后报给火电厂商，火电厂商则在最大化联盟合作剩余的基础上进行机组功率调整。在该过程中，新能源通过火电厂商的配合调整形成的主要效益变化包括：增加了新能源的并网电力提高了电量收益；减少了负荷波动从而减少了辅助服务费用和分时段交易合同考核费用；减少了火电厂商的出力从而减少了煤耗成本和碳排放成本；同时火电机组的上下调过程中不可避免地有一部分的运行损耗成本的提升，这些内容构成了联盟的合作剩余变化。

据此可以分析出多能互补的合作博弈过程中有如下关键要素。

1)参与者：新能源厂商和火电厂商，通过形成新能源火电多能互补的打捆结构参与电力市场交易，提高新能源消纳能力并推进双碳建设。

2)策略集：新能源厂商与火电厂商的分时段打捆出力。

3)特征函数：新能源厂商与火电厂商的合作收益W最大化。

2.3 合作博弈模型构建

构建新能源厂商与火电厂商的合作博弈模型特征函数如公式(4)所示。

其中：W1为 新能源与火电联盟的总收益；Wn为新能源厂商收益；Wf为火电厂商收益；C为偏差考核成本。

新能源厂商与火电厂商的收益情况分别如公式(5)和公式(6)所示。

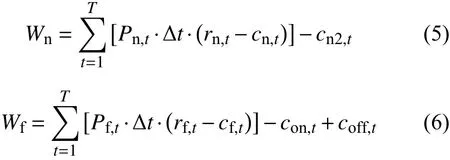
其中：T 为时段t的 总数；Δt为各个时段的时长；Pn,t为可再生能源厂商在t时 段的出力；Pf,t为火电厂商在t时段的出力；rn,t、rf,t分别为新能源与火电在t时段的度电收益，在本文体现为电力市场的分时段电价；cn,t、cf,t分 别为新能源与火电在t时段的度电成本；cn2,t为新能源在t时段的弃电成本，用以体现新能源与火电打捆带来的新能源消纳电力提升效益； con,t为t时 段火电的开机成本； coff,t为t时段火电的停机成本。

对应成本的计算方式如公式(7)—(9)所示。

其中：ε为惩罚系数；Po,t为新能源厂商在t时段的预测出力；gt为火电机组在t时段的开停机状态，开启为1、关闭为0；ron,t、roff,t分别为火电机组在t时段的开机成本和停机成本。

偏差考核成本如公式(10)所示计算方式。

式中：Pl,t为电力市场分时段合约电量；ch、 cl分别为正负偏差的度电考核费用。

同时考虑新能源与火电打捆比例约束如公式(11)所示。

其中：Qn为新能源电量；Qf为火电电量；λ为新能源与火电的打捆比例。

对于火电厂商，出力约束如公式(12)所示；机组爬坡约束如公式(13)所示；开停机时间约束如公式(14)、公式(15)所示。

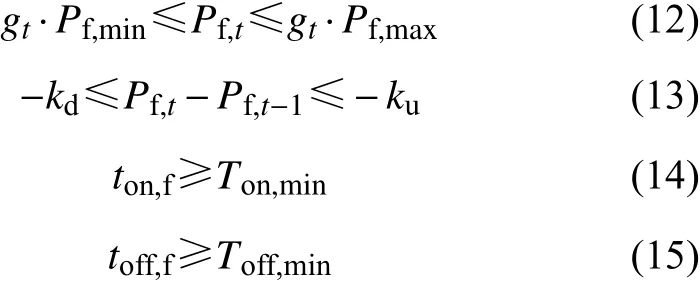
式中： Pf,min、 Pf,max分别为火电机厂商的最大最小出力；-kd、-ku分别为火电厂的上下爬坡速率；ton,f、toff,f分别为机组的开停机持续时间；Ton,min、Toff,min分别为机组的最短开停机持续时间。

对于打捆电量有潮流约束如公式(16)所示。

式中： Pmin、 Pmax分别为新能源厂商和火电厂商传输功率的断面功率传输下限和断面功率传输上限。

2.4 火电厂商和新能源厂商的利益分配策略

在合作博弈过程中，采用Shapley值理论进行效益分配，则有如公式(17)所示效益分配策略。

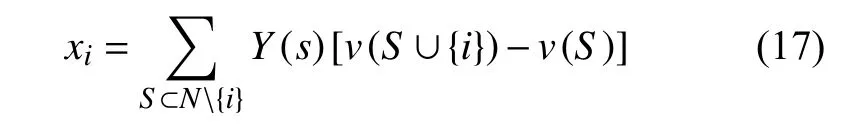
其中：Y(s)为联盟成员的分配系数，其计算公式如公式(18)所示；S 为合作联盟去除成员i后的联盟总成员； N{i}为 去除成员i后的联盟成员。

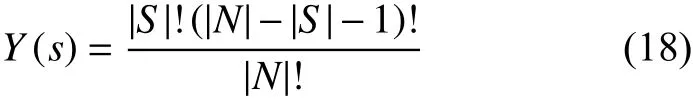
但是考虑到火电厂商在该过程中的贡献问题[24]，引入修正因子进行效益分配调整，则如公式(19)所示的效益分配函数。

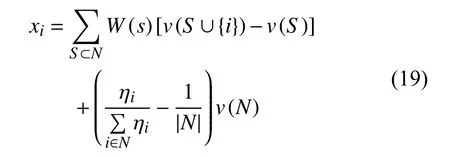
其中：ηi为 联盟成员i的修正系数；代表联 盟成员i的修正值与平均值的差值。

2.5 博弈效果测算

为评价合作博弈过程中带来的效益增量，对联盟形成前的火电厂商和新能源厂商的市场效益进行测算，分别如公式(20)和公式(21)所示的市场剩余。

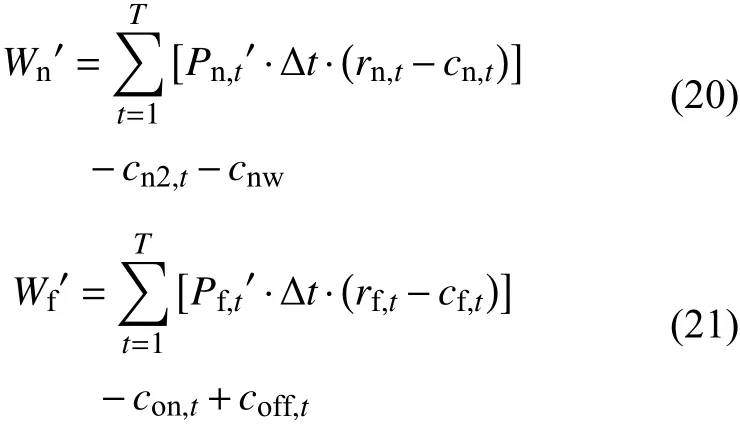
其中：Wn′为原始新能源厂商的市场效益；Pn,t′为原始新能源厂商的并网电力；cnw为新能源厂商的偏差考核费用，其计算方式如公式(22)；Wf′为火电厂商的原始市场效益；Pf,t′为火电厂商的原始并网电力。

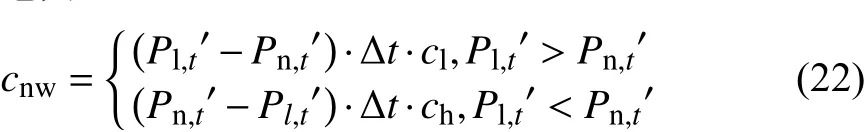
其中 Pl,t′为新能源厂商在t时段的合约电量。

据此计算联盟实现和增量效益Δw1如公式(23)所示。

3 考虑源荷互动的合作博弈模型

3.1 考虑多能互补的博弈策略

本节以可调大用户与新能源厂商之间的协调互补研究基于源荷互动的新能源参与电力市场交易策略。在该过程中，通过构建新能源厂商与可调大用户的电力联盟，降低新能源厂商的弃电损失和偏差考核费用，同时也节约可调大用户的用电成本，双方都获得增量收益，满足成立联盟谋取合作剩余的基础条件。特别说明的是，储能资源作为荷端的一部分，在本节中视作为一种特殊的可调负荷，由于其本身不具备负荷消耗特征并且能储备电力而具备百分百的调节能力。

成立源荷互动联盟之后，新能源厂商根据发电预测电量变化情况与可调大用户商定负荷调节方式，以使得联盟的净出力曲线趋于平稳，并合理调节分时段并网电量的物理执行情况。该过程中，新能源厂商通过与可调大用户的之间的友好互动创造的主要效益变化包括：增加了新能源的并网电力提高了电量收益；减少了负荷波动从而减少了新能源厂商的辅助服务费用和分时段交易合同考核费用；可调大用户消纳弃电节约了用电成本；并通过消纳新能源电力获得绿证和配额效益等，这些内容构成了联盟的合作剩余变化。

据此可以分析出多能互补的合作博弈过程中有如下关键要素。

1)参与者：新能源厂商和可调大用户，通过形成新能源与需求侧用户的源荷互动结构参与电力市场交易，提高新能源消纳能力并推进双碳建设。

2)策略集：新能源厂商与可调大用户的分时段出力和负荷。

3)特征函数：新能源厂商与可调大用户的合作收益W2最大化。

3.2 合作博弈模型构建

构建新能源厂商与可调负荷用户的合作博弈模型特征函数如公式(24)所示。

其中：W2为 新能源与可调负荷联盟的总效益；Wl为可调负荷用户的市场效益，其计算方式如公式(25)所示。

其中：Pl,t为可调负荷在t时段消纳的可再生能源电力；pl,t为 可调负荷在t时 段的原始电价；pr,t为在t时段的弃电消纳电价；Gl为可调负荷实现的绿证收益；CB为可调负荷中储能的运维成本。

在调节过程中，可调大用户有调节容量限制如公式(26)所示；当日总电量需求约束如公式(27)所示。

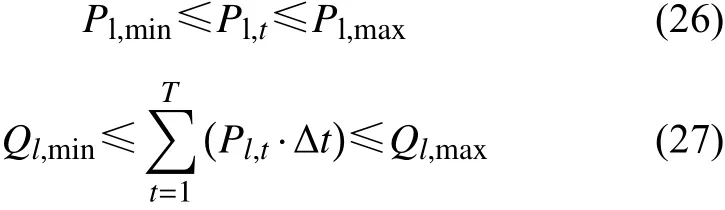
其中：Pl,min为可调大用户的最低消纳功率，对于特殊可调负荷储能资源来说，Pl,min为最大放电功率-PB,out；Pl,max为可调大用户的最高消纳功率，对于特殊可调负荷储能资源来说， Pl,max为最大充电功率PB,in；Ql,min为当日可调大用户的最低电量需求，对于特殊可调负荷储能资源来说，其值为0；Ql,max为当日可调大用户的最高电量需求，对于特殊可调负荷储能资源来说，其值为储能容量B。

3.3 可调大用户和新能源厂商的利益分配策略

在效益分配过程中同样考虑可调大用户的贡献度，引入修正因子进行效益分配调整，则有如公式(28)所示的效益分配函数。

其中：θi为可调大用户与新能源厂商联盟中成员i的修正系数；代 表联盟成员i的修正值与平均值的差值。i∈N

3.4 博弈效果测算

为评价合作博弈过程中带来的效益增量，对联盟形成前的可调大用户和新能源厂商的市场效益进行测算，新能源厂商有如公式(20)所示的市场剩余，可调大用户有如公式(25)所示的市场剩余。

据此计算联盟实现和增量效益Δw2如公式(29)所示。

4 仿真算例

基于多能互补和源荷互动的新能源消纳场景，本文以新能源电厂A与火电企业B以及可调大用户C为例，构建可再生能源消纳的典型场景，对本文所提合作博弈模型进行验证。设置新能源预测出力曲线如图3所示；可调大用户的初始负荷曲线如图4所示；电力市场分分时段电价如表1所示；新能源厂商与火电厂商的分时段电力合约如表2所示。电力市场合约考核费用按5%计算；风火打捆比例按1:5计算；设置火电厂商和新能源厂商的效益分配修正系数ηi分别为0.56和0.44；设置可调大用户厂商和新能源厂商的效益分配修正系数θi分别为0.58和0.42；输配电价及其各项附加费用为170元/MW·h；火电标准煤耗按0.29 kg/MW·h计算；煤价按0.57元/kg计算；考虑到绿证市场和碳市场数据的稳定性较弱，暂时不予考虑。求解过程采用MATLAB约束优化工具箱进行。

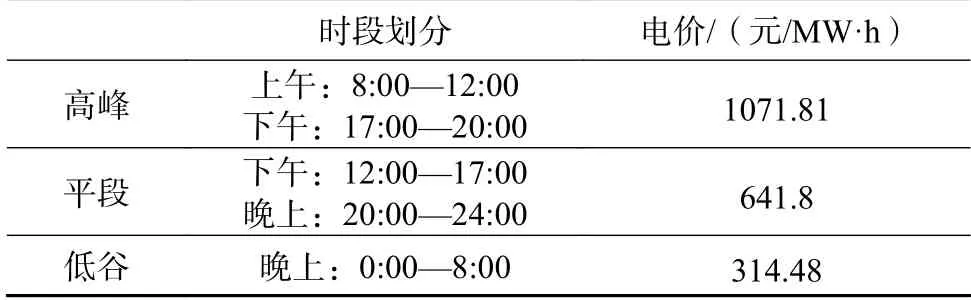
表1 电力市场用户侧分时段电价Table 1 User side TOU price of electricity market

表2 新能源厂商与火电厂商的分时段电力合约Table 2 Time-phased electricity contract between new energy manufacturers and thermal power generation companies

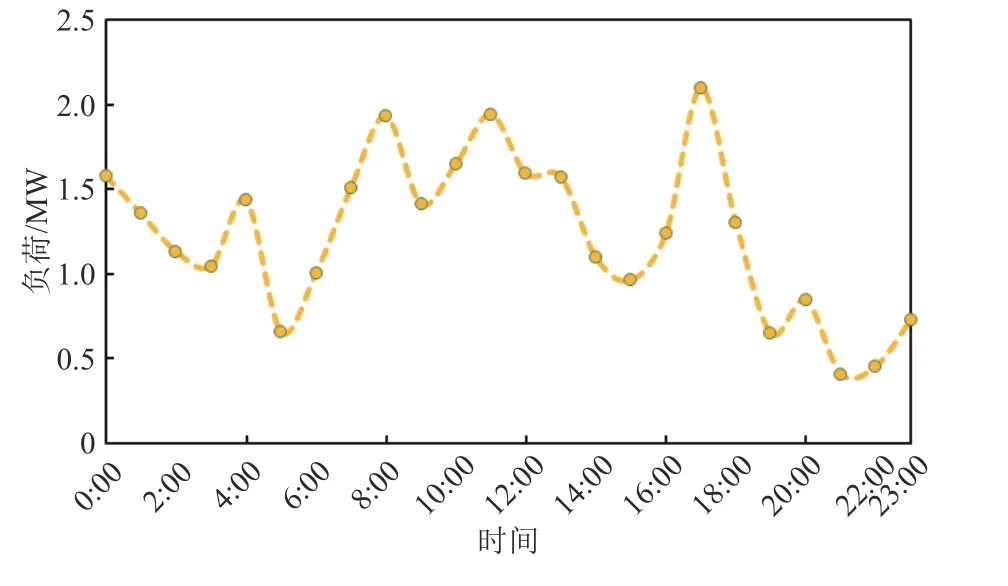
图3 新能源预测出力曲线Fig.3 Forecast output curve of new energy

图4 可调大用户初始负荷曲线Fig.4 Adjustable initial load curve of big consumer

在考虑多能互补的新能源消纳场景中，通过博弈优化得到新能源消纳曲线的变化情况如图5所示，实现火电厂商与新能源厂商打捆分时段电力合约履约情况如表3所示。

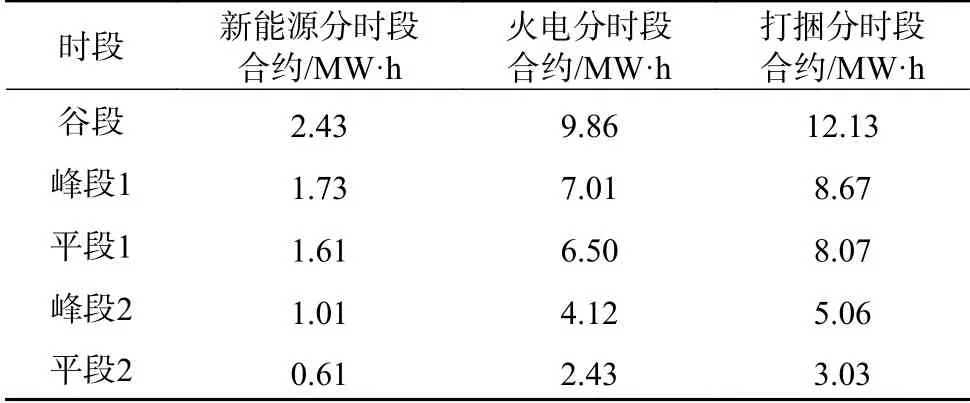
表3 火电厂商与新能源厂商的分时段电力合约履约情况Table 3 Time-phased electricity contract between new energy manufacturersand thermal power generation companies

图5 考虑多能互补的新能源消纳曲线Fig.5 New energy consumption curveconsidering multienergy complementarity

相对于无合作博弈过程中的新能源原始履约收益2846.04元/日以及火电厂商的原始履约15512.97元/日，通过火电协调新能源出力增加了新能源的履约量并提升了整体电力出售水平，实现新能源消纳3872.65元/日，实现火电售电收益15678.16元/日。具体来说，火电厂商及时调整出力实现了新能源电力的全额消纳，增加新能源消纳1.35 MW·h、占比约22.32%；减少新能源厂商的偏差考核费用51.33元/日；实现新能源厂商增量收益547.12元/日，收益提升幅度达19.22%；实现火电厂商增量收益696.34元/日；实现多能互补效益总提升1192.13元/日。可见通过火电与新能源之间的打捆交易，有效促进了新能源的消纳和各方收益的提升。

在考虑源荷互动的新能源消纳场景中，通过博弈优化得到新能源消纳曲线的变化情况如图6所示。

图6 考虑源荷互动的新能源消纳曲线变化Fig.6 Change of new energy accommodation curve considering source-charge interaction

相对于无合作博弈过程中的新能源原始履约收益2846.04元/日以及可调负荷的原始用电成本4930.97元/日，原始用户考核偏差51.33元/日；通过灵活性负荷的协调作用，实现新能源消纳3685.10元/日，实现可调负荷用电成本4544.22元/日，用户考核偏差降低值9.38元/日。具体来说，通过可调大用户及时响应新能源的负荷调节需求，增加了新能源消纳0.98 MW·h、占比约16.21%；减少新能源厂商的偏差考核费用41.95元/日；实现新能源厂商增量收益532.46元/日，收益提升幅度达18.71%；实现可调大用户增量收益735.30元/日；实现源荷互动效益总提升1267.75元/日。可见，通过可调大用户的调节有力地促进了新能源消纳，提升了新能源厂商的售电收益、节约了新能源厂商的考核成本，并提升了可调节大用户的市场收益。

5 结论

高占比新能源消纳是新型电力系统建设过程中不可避免的重要问题。本文从新能源参与电力市场的角度出发，针对新能源并网消纳问题、市场效益问题、偏差考核问题等进行综合考虑，构建基于合作博弈模型的新能源消纳策略，有效提升了新能源的并网消纳能力、提升了市场效益并一定程度上缓解了偏差考核费用。具体来说，有如下几方面的研究成果：

1)构建考虑多能互补的合作博弈模型，通过火电与新能源电力的打捆交易实现打捆电力的稳定输出，避免了新能源厂商高额的偏差考核费用和弃电损失，实现了高比例新能源的消纳，并减少了火电的煤耗成本，实现了多能互补联盟的效益提升。

2)构建考虑源荷互动的合作博弈模型，通过可调大用户与新能源之间的灵活互动实现新能源电力的稳定输出，缓解了新能源厂商的分时段偏差考核成本和弃电损失，实现了高比例新能源的消纳，并为可调大用户提供了更低用电成本，实现了源荷互动联盟的效益提升。

3)结合现阶段分时段中长期交易和绿电交易的市场特征，充分考虑分时段合约的特点、偏差考核和大用户对绿电的需求等多方因素进行优化模型设计和优化效果提升，并应用算例验证了模型对于新能源消纳、市场发展等方面的有益效果。

本文基于现阶段电力市场发展初期的设定，并未对火电、新能源以及可调负荷三方之间的协调互补进行深入分析和研究，充分考虑各方之间的物理联络关系和效益分配关系设计三方合作联盟关系是下一步研究方向。

致谢

本文得到了国家电网公司基于高占比新能源环境的电力曲线中长期交易机制研究项目(SGTYHT/19-JS-215)的资助，在此表示感谢。