基于有效干扰系数的MSK 干扰效能分析

陈增茂，闫倩，孙志国，孙溶辰

（哈尔滨工程大学信息与通信工程学院，黑龙江 哈尔滨 150001）

0 引言

无线电通信对抗已成为现代作战的一种重要手段，在现代战争中发挥着越来越重要的作用。通信对抗表现形式为敌对双方对传输通信信号的破坏和保护，即通信干扰与抗干扰相互博弈的过程[1]。在通信对抗中，干扰效能是评估干扰方破坏能力或削弱通信方通信能力的重要手段。

通信干扰效能的评估指标很多，包括能量、空间、频率等，目前尚无公认的统一标准。根据评估指标数量的多少，通信干扰效能评估可分为多指标评估和单指标评估。在多指标评估中，潘志丽等[2]提出以有效干扰效果评估因子衡量干扰效果，干扰效果评估因子与能量、空间、时间和干扰方式等因素有关；辛晓晟等[3]提出通过干扰距离、通信压制距离、干通比、通信有效区域面积4 个指标评估干扰效能。在单指标评估中，刘广建等[4]通过计算接收信号和有用信号的相关系数来衡量干扰效果；李源等[5]把相关系数的概念引入二维数组，对干扰图像和目标真实图像做相关系数分析，衡量干扰效果。在通信干扰效能评估中，很多学者以被干扰接收机的误码性能作为衡量标准[6-25]。目前，通信干扰效能分析大多针对非相干接收机和非正交接收机，鲜有文献分析正交接收机的误码性能。

通信干扰技术的另一个发展趋势是以相干干扰为代表的高效干扰[18]技术应用越来越广。因此，本文借鉴文献[4-5]中接收信号与通信信号的相关系数思想，提出了将有效干扰系数作为干扰效能评估指标，分析其对正交接收机的影响，通过推导接收机理论误码率进行干扰效能评估。

最小频移键控（MSK,minimum shift keying）广泛应用于各种通信系统，但现有针对MSK 信号的干扰效能分析大多基于传统的单音干扰[17]和多音干扰[14-16]。因此，本文针对相干干扰场景下的MSK 正交接收，利用所提有效干扰系数，通过推导理论误码率进行MSK 干扰效能分析。假设干扰方已通过通信侦察获取了通信信号的部分特征信息，包括载波频率、信号带宽、调制进制，根据侦察所得先验信息，干扰方对通信方施加一系列相干干扰。以干扰信号和通信信号的相关分析为依据，以响应与激励的关系为出发点，分析干扰信号对通信系统造成有效干扰的机理，并推导理想情况下二进制频移键控（2FSK,binary frequency shift keying）、MSK、二进制相移键控（2PSK,binary phase shift keying）和二进制振幅键控（2ASK,binary amplitude shift keying）干扰对MSK 通信系统的影响，以及非理想情况下干扰对MSK 通信系统的影响。

1 干扰响应与干扰效能分析

如图1 所示，将正交接收机看作线性时不变（LTI,linear time invariant）系统，不同激励作用于LTI 系统时会产生不同的响应。当高效干扰和噪声存在时，可将接收机视为多输入多输出的线性时不变系统。设通信信号为s(t)，其经过接收机后输出为通信响应α(t)。干扰信号j(t)与噪声信号n(t)经过接收机后输出为干扰响应β(t)和噪声响应γ(t)。

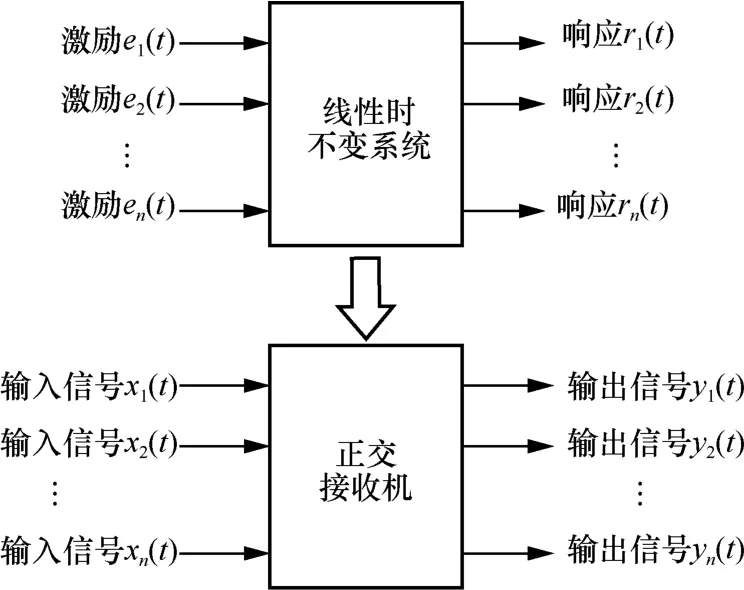
图1 LTI 系统与正交接收机

1.1 正交接收机干扰响应模型分析

信号与多维矢量的表达形式类似，因此可借助二者之间的相似性，将信号中的抽象问题化解为容易理解的矢量问题进行分析，利用数学推导解决实际工程中的问题。假设信号可以分解为x与y二维的形式，且x方向为通信信号的方向。由于通信信号和接收机是合作关系，x方向也是信号能顺利通过接收机的方向。如图2 所示，j1(t)和j2(t)为2 个能量大小相同的干扰信号，其对于x方向的投影分别为x1和x2。尽管2 个干扰信号对通信接收机作用的能量相同，产生的干扰效果却不同。显然j1(t)对通信方的破坏能力更强。

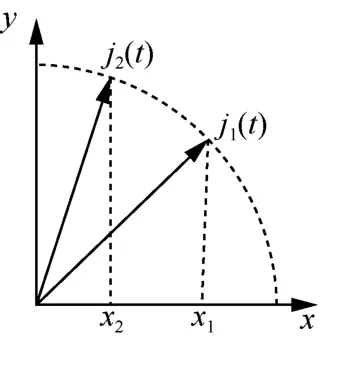
图2 不同干扰的空间映射示意

本文借鉴相关系数理论[4-5]，将干扰与通信信号相关干扰系数cjs定义为

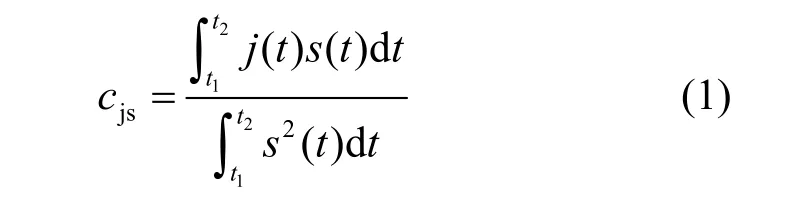
将cjs理解为干扰信号j(t)中含有通信信号s(t)方向的分量，即j(t)在s(t)方向上的投影。因此，干扰信号通过接收机后产生的干扰响应为β(t)=cjsα(t)，接收机的总响应为z(t)=α(t)+cjsα(t)+γ(t)。

当接收机为正交接收机时，应分别考虑I、Q两路接收情况。此时，两路的相关干扰系数组成有效干扰系数共同对接收系统造成影响。本文以MSK信号的正交解调为例做出相关分析。

当通信信号s(t)为MSK 时，已调信号可表示为

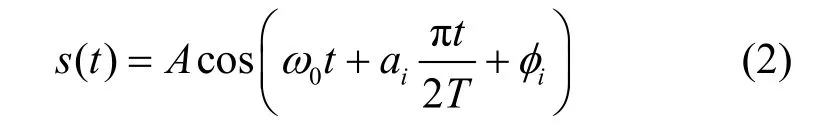
其中，A为调制幅度，ω0=2πf0为中心角频率，ai为第i个码元的双极性数据信息，取值为 ±1，T为基带信号码元宽度，即码元传输速率Rb的倒数，φ i为初始相位。s(t)可以通过正交调制表示为

当接收信号r(t)中包含干扰信号j(t)时，可根据式(1)求得MSK 正交接收机I、Q 路的相关干扰系数分别为

分析MSK 信号误码性能时，分别计算I 路和Q路误码率Pei和Peq，并由差分译码规则得到总误码率为

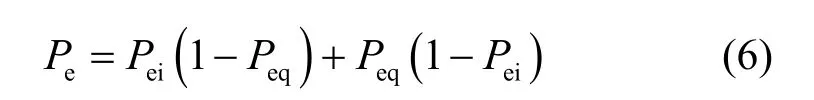
1.2 整体干扰效能分析

为分析MSK 信号在加性白高斯噪声（AWGN,additive white Gaussian noise）下施加高效干扰时的干扰效能，搭建MSK 正交调制解调干扰效能分析整体模型，如图4 所示。

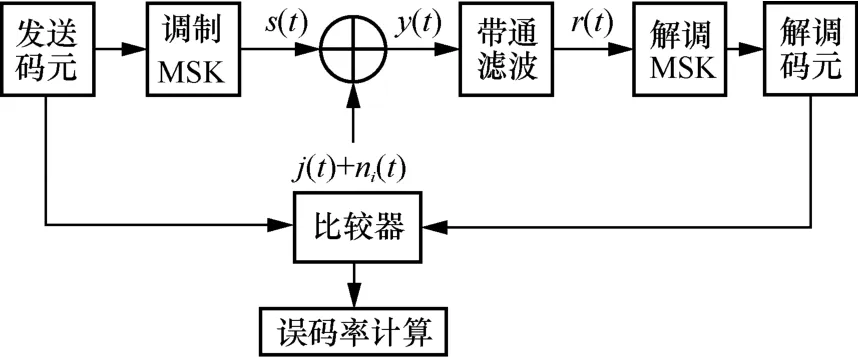
图4 MSK 正交调制解调干扰效能分析整体模型

图4 中，ni(t)为高斯白噪声，经过带通滤波器后为窄带高斯白噪声n(t)，其均值为0、方差为。n(t)可分解为

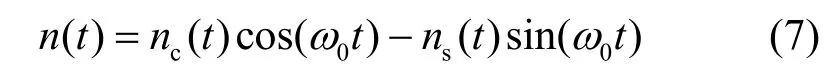
其中，j(t)为施加的干扰信号，则接收机输入端的信号为

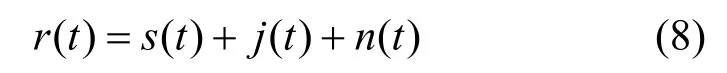
设通信信号、干扰信号经过I 路接收机后产生的响应为ξ，则。噪声信号进入I 路接收机产生的噪声响应为

经计算，γI(t)是均值为0、方差为的高斯白噪声，则图3 中的判决值ZI(t)是均值为ξ、方差为的高斯白噪声。

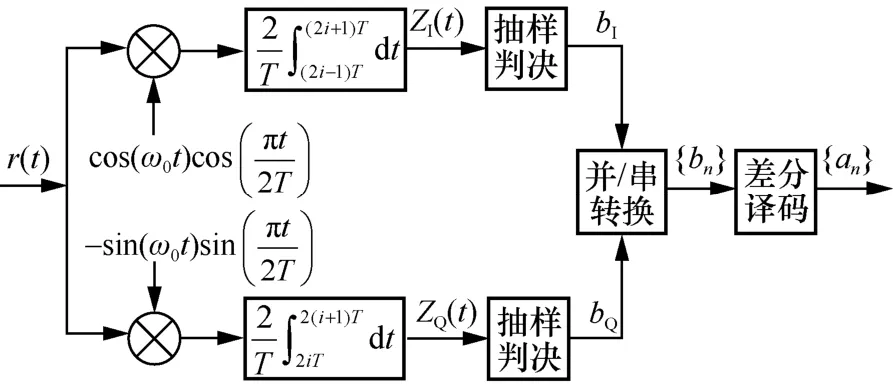
图3 MSK 信号正交解调过程

接收机未能察觉干扰信号存在，仍会按照最佳判决门限判决。因此判决信号的概率密度函数为Q 路接收机的分析与I 路类似，因此可求得Q路信号的误码率为

2 典型数字调制干扰下干扰效能分析

2.1 理想情况下干扰效能分析

对于二进制通信系统，理论上干扰机发送与发射机完全相反的码元可获得最佳干扰效果。但是实际上干扰方无法预知通信方的发送码元信息，因此本文分析典型二进制调制方式的随机码元干扰对通信信号误码性能的影响。当干扰信号为2FSK 时，时域表达式为

MSK 两条支路码元持续时间都为2T，而2FSK干扰信号的码元持续时间为T。因此，在I 路积分区间内干扰信号发送2 个码元信息a1和a2。此时，I 路相关干扰系数cjsI的分子可以拆分成两部分

表1 干扰信号、相关干扰系数以及Q 路误码率关系

当dQ(t)等概率发送 “+1”和“–1”时，Q路接收机的误码率为

当干扰信号为2ASK、2PSK、MSK 时，按照类似的方法可求出误码率通式，如表2 所示。

表2 干扰信号每路误码率通式

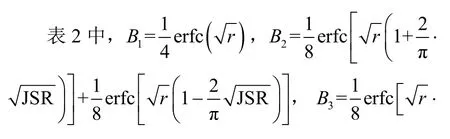
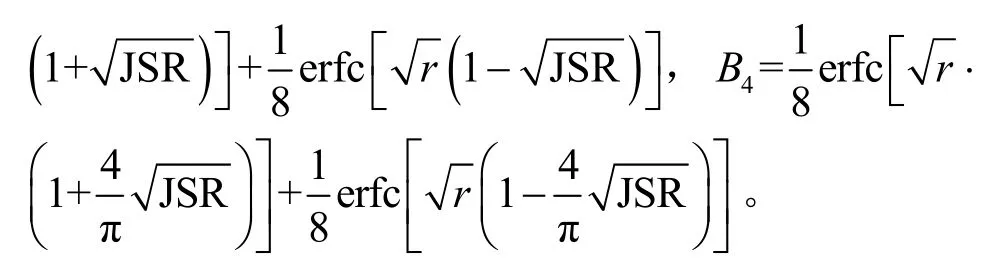
2.2 非理想情况下干扰效能分析

2.1 节是在理想状态下得到的结论，然而在实际情况中干扰信号的传输过程并非理想信道，干扰与通信信号往往存在不完全同步问题，这会影响干扰信号对接收机的干扰效能。为完善数学模型，本节分析干扰信号为MSK 时相位差、频差和时延对干扰效能的影响。

2.2.1 相位差对干扰效能的影响

当干扰信号与通信信号存在相位差时，假设随机相位偏移量为ψ，干扰信号可表示为

其中，ψ在0～2π 随机分布。通信码元与MSK 干扰码元的时序关系如图5 所示。

图5 通信码元与MSK 干扰码元的时序关系

以计算通信码元D4误码率为例进行分析。D4的解调与Q3和 I4有关。首先分析Q3的误码率，当干扰信号存在相位差时，解调Q3与干扰信号的2′、3′、4′码元均有关。因此Q3的相关干扰系数为

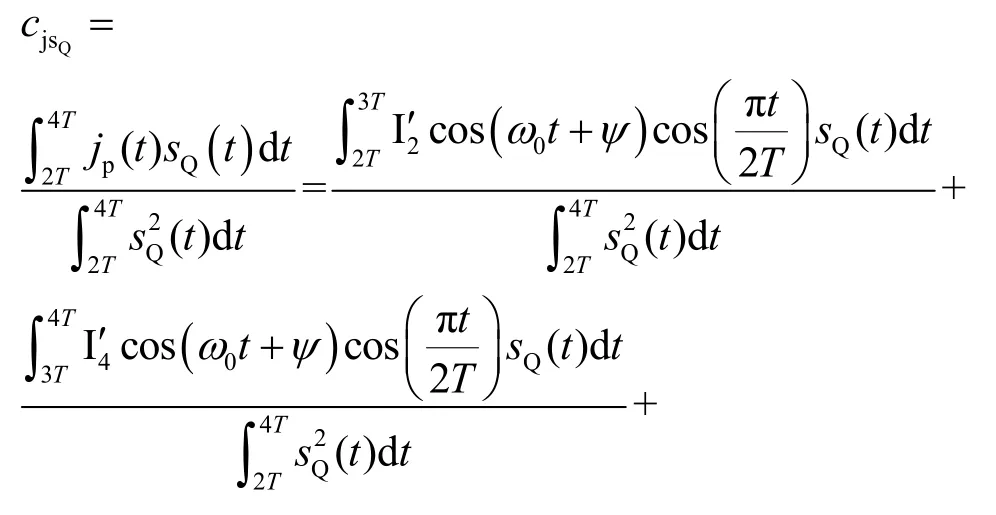
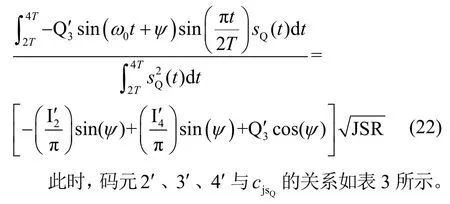
Q 路接收机的误码率为

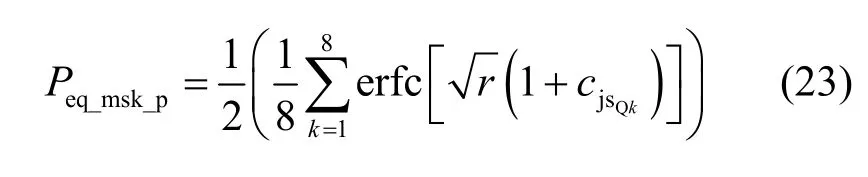
同理，可以求出I 路接收机的误码率与Q 路相同，即

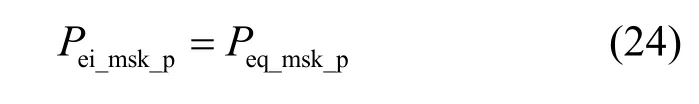
2.2.2 频差对干扰效能的影响

当接收机或干扰机有一方非固定时，多普勒效应接收机接收到的干扰信号频率与干扰机发射频率有所不同。假设在接收机输入端干扰信号与通信信号的频差为Δf，则干扰信号可表示为

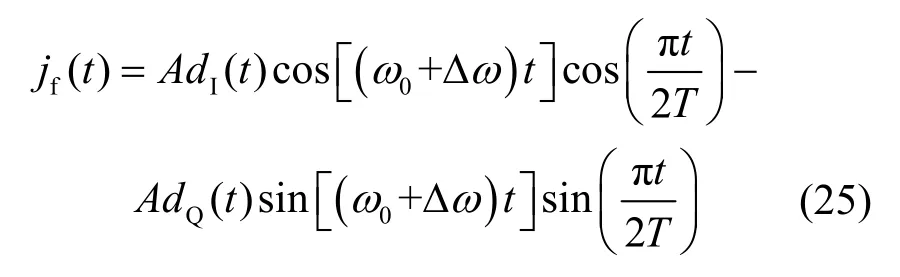
其中，Δω=2πΔf。分析过程与2.2.1 节类似，可求出Q 路接收机的相关干扰系数为

与2.2.1 节计算方法类似，可求出MSK 干扰存在频差时的误码率公式。

2.2.3 时延对干扰效能的影响

虽然干扰机能够获得通信信号的调制方式、载波等关键信息，但是干扰机处理信息需要时间且信道有很多不确定性，干扰信号无法与通信信号完全对齐。假设接收机输入端的干扰信号与通信信号的时延为τ，因此干扰信号可表示为

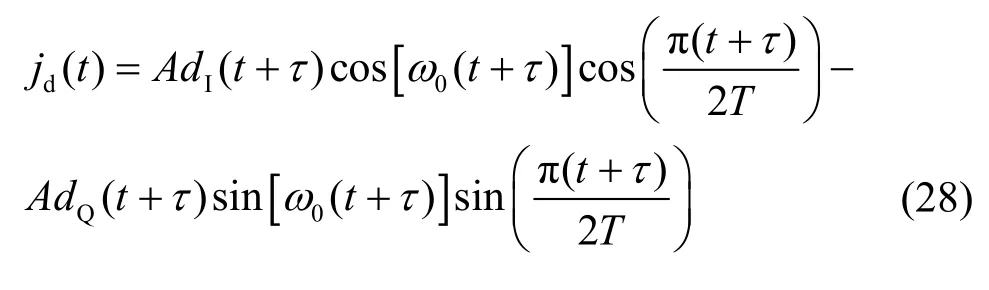
其中，τ在0～2T随机分布。

存在时延的通信码元与MSK 干扰码元的时序关系如图6 所示。设通信信号第一个码元到达接收机时刻为0，干扰信号滞后通信信号τ。与2.2.1 节类似，对通信码元Q3的解调进行分析，由于时延的存在，干扰码元都将对Q3产生影响，且干扰区间分别为[2T,2T+τ]、[2T+τ,4T]、[2T,3T+τ]和[3T+τ,4T]。

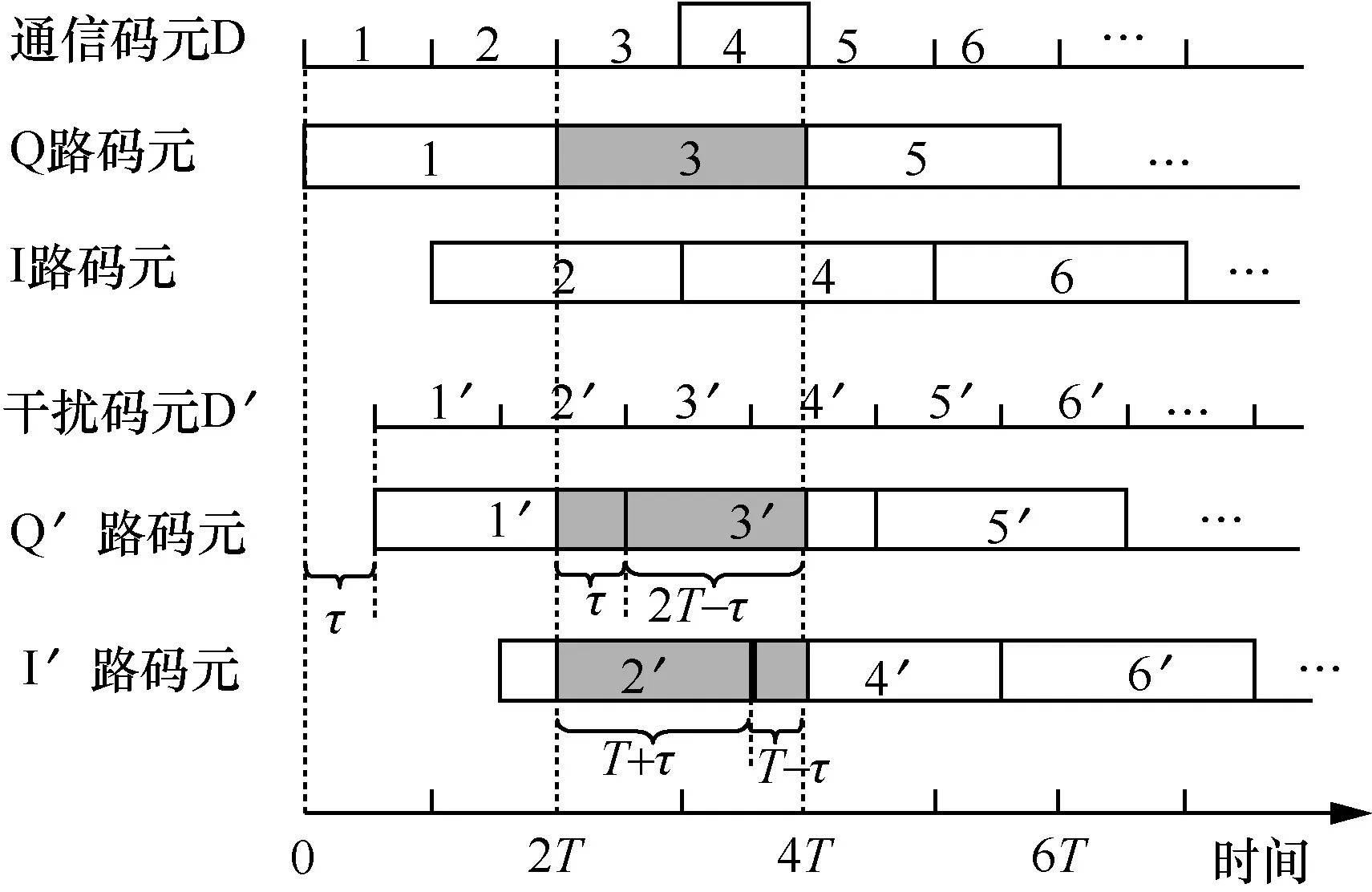
图6 存在时延的通信码元与MSK 干扰码元的时序关系

因此，可求出Q 路相关干扰系数为

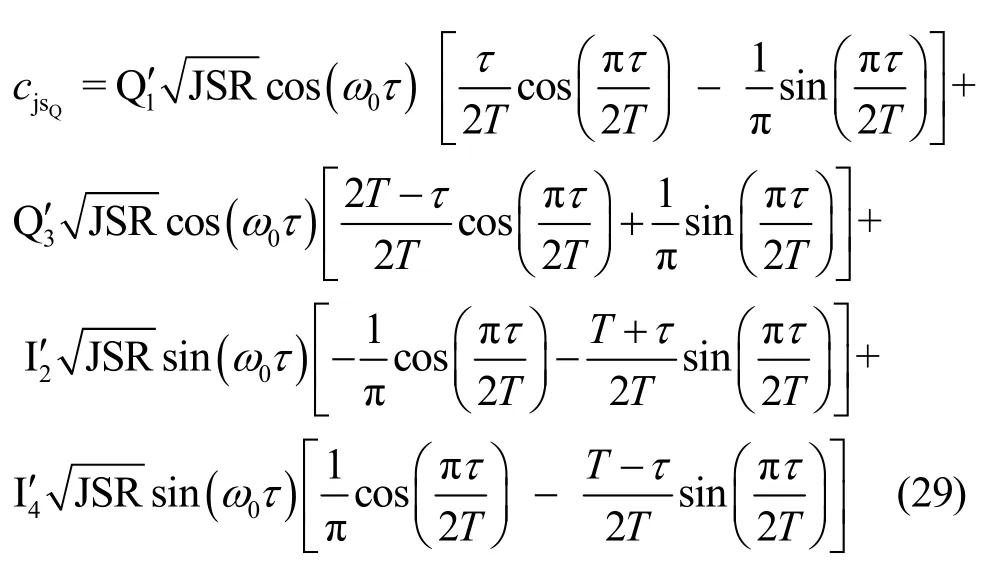
此时，干扰码元共有 24种取值，假设l=1时1′=+1、2′=+1、3′=+1、4′=+1（取值规则与表3类似），则Q 路误码率为

表3 码元 2′、3 ′、4 ′与的关系

表3 码元 2′、3 ′、4 ′与的关系

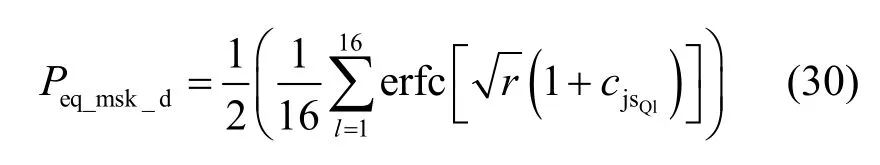
同理，可求得I 路误码率为

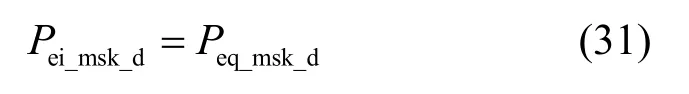
3 仿真分析

为验证本文理论分析的正确性，本节仿真4 种典型数字调制干扰信号在理想情况下通信系统的误码性能，以及MSK 干扰存在频差、相位差和时延情况下通信系统的误码性能。本文仿真中，载波中心频率为1 MHz，码元宽度为1 ms。

不同干信比下干扰样式对干扰效能的影响如图7 所示，具体参数如下：信噪比为0 dB，干信比为-20～20 dB。从图7 可以看到，2ASK 与2PSK干扰效能相近，2FSK 与MSK 干扰效能相近。因此，将干扰分为两组进行对比分析。

图7 不同干信比下干扰样式对干扰效能的影响

1) 2ASK 与2PSK 干扰分析

由表2 可知，2ASK 与2PSK 这2 种干扰样式下的Q 路误码率相同，为AWGN 下的干扰效能。由于这2 种干扰信号均为余弦形式与Q 路的正弦载波正交，因此对Q 路不产生影响。2ASK 与2PSK的干扰效能主要取决于I 路。当JSR 较小时，2PSK的干扰效能优于2ASK。从时域角度分析，对于通信信号的I 路，同样是发送“0”码时，2ASK 信号不会对通信信号产生影响，但是2PSK 信号依然会持续发送波形，从而影响通信信号接收机的接收质量。

2) 2FSK 与MSK 干扰分析

2FSK 与MSK 这2 种干扰对I 路的影响相同，主要区别为Q 路。当JSR 较小时，MSK 的干扰效能优于2FSK，从频域角度分析，2FSK 信号虽然与MSK 信号同频，但因为MSK 信号具有相位连续的特点，能量更加集中，从而在干扰时能对接收机接收到的信号造成更大的干扰。

将信噪比0 dB 代入表2，当JSR 足够大时，干扰信号完全破坏通信系统的传输，接收机将按照干扰机的发送波形解调。此时，MSK 和2FSK 干扰效能相同，误码率约为0.5；2ASK 干扰效能优于2PSK，误码率分别约为0.41 和0.32。

图8 和图9 仿真了干扰样式和信噪比对干扰效能的影响，信噪比为-10～20 dB，干信比分别为0 dB 和–5 dB。从图8 和图9 可以看出，当干信比较大时，干扰效能的主要影响因素为干扰样式。干扰效能由强到弱排序为MSK、2FSK、2PSK、2ASK。

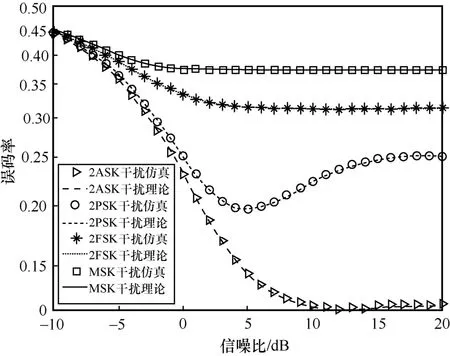
图8 干信比为0 dB 时干扰样式和信噪比对干扰效能的影响

从图9 可以看出，当信噪比小于10 dB 时，4 种干扰样式中MSK 的干扰效能最强；当信噪比大于10 dB 时，2PSK 的干扰效能最强。因此，此分析结论对干扰决策具有重要的指导意义，为获得更佳的干扰效果，应根据被干扰信号的信噪比，选取不同的干扰样式。

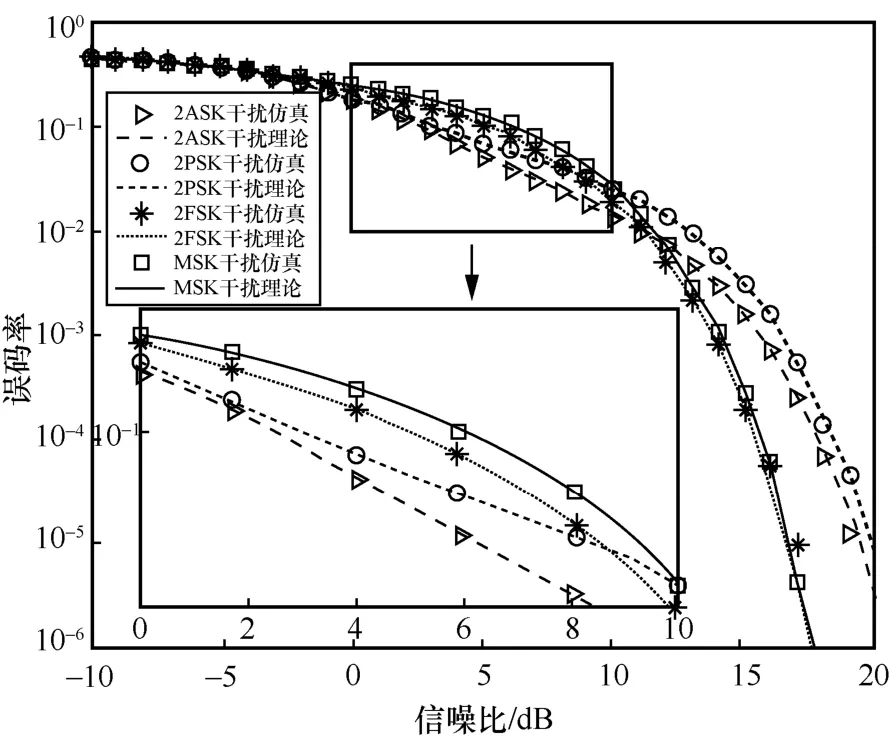
图9 干信比为-5 dB 时干扰样式和信噪比对干扰效能的影响

图10～图12 仿真了非理想情况下通信系统的误码性能，选取MSK 为干扰样式，干信比为–5 dB，信噪比为–10～10 dB。

图10 相位差对干扰效能的影响

图11 为频差对干扰效能的影响，频差分别选取0、0.3f0、0.5f0和0.8f0。从图11 可以看出，当存在频差时，误码率曲线几乎重合，干扰效能逊于无频差时。原因是干扰效能对频差较为敏感，当干扰信号与MSK 通信信号存在频差时，相干接收机几乎可以滤除全部干扰。分析式(26)和式(27)可得，相关干扰系数约为0 时，干扰效能和AWGN时近似。

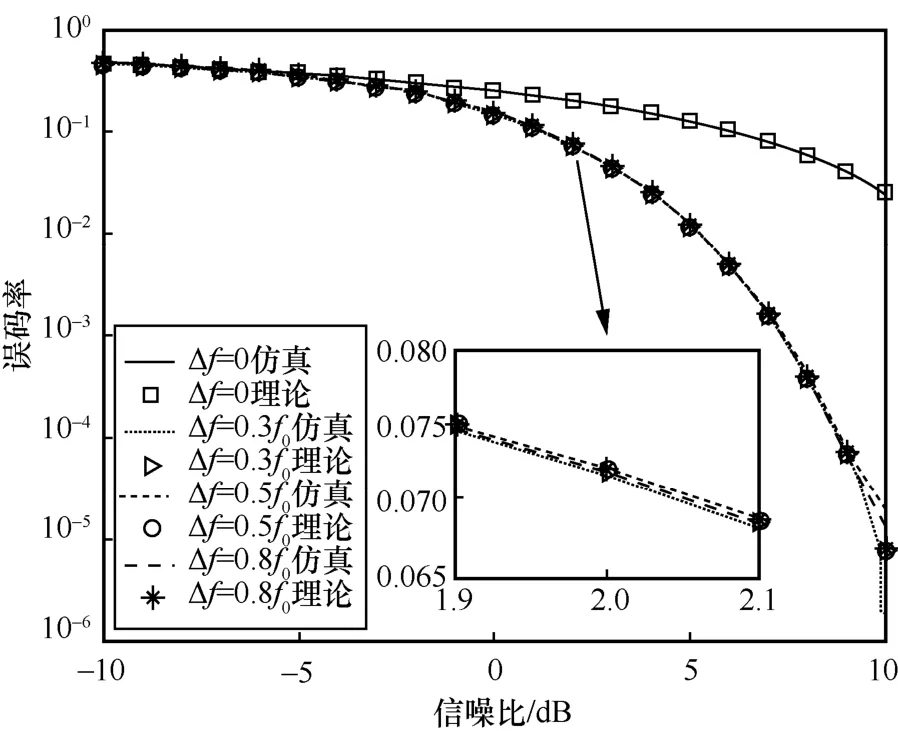
图11 频差对干扰效能的影响

图12 为时延对干扰效能的影响，时延分别选取0、0.3T、0.5T和0.8T。从图12 可以看出，时延对干扰效能的影响较大且比较有规律。随着时延的减小，干扰效能逐渐增强。当时延为0 时，干扰效能最强。

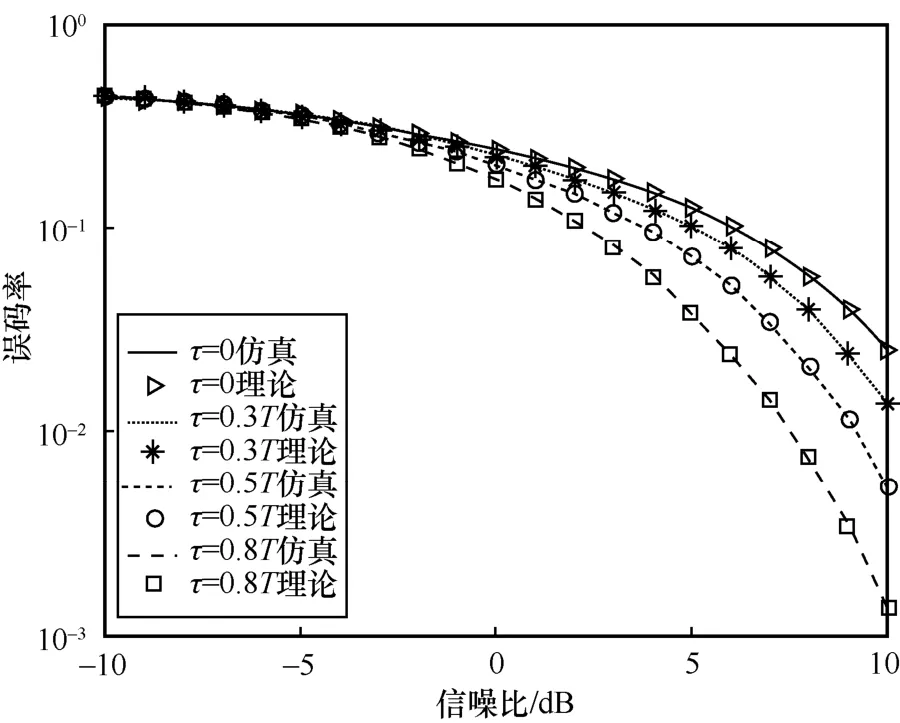
图12 时延对干扰效能的影响

受限于篇幅原因，非理想情况时本文仅仿真干信比为-5 dB 时的情况。当干信比增加或减小时，误码性能整体随干信比增加或减小，但相对误码性能与干信比-5 dB 时基本一致。

4 结束语

本文针对正交接收机干扰效能评估问题，通过计算干扰和通信信号的关联程度，提出了有效干扰系数作为干扰评估参数，进而推导了接收误码率进行干扰效能分析。本文以MSK 通信信号为例，考虑多种典型二进制数字调制信号作为相干干扰源的场景下，利用所提有效干扰系数，进行MSK 干扰效能分析。另外，本文还考虑了非理想通信侦察场景下相干MSK 的干扰效能，推导得到相应误码率修正公式。数值仿真结果验证了本文方法的准确性和有效性。通过分析发现，在典型二进制数字调制干扰中，MSK 并非总是最佳干扰样式；为获得最佳干扰效果，干扰机应根据被干扰MSK 信号的信噪比选择不同的干扰调制样式。本文的研究对通信干扰引导和干扰决策具有较好的现实指导意义。