稀疏图的k-frugal列表染色

房启明，张 莉

（同济大学数学科学学院，上海 200092）

本文仅讨论无向的有限的简单图，未提及的定义和定理参见文献［1］。对于一个点v，用dG(v)、NG(v)（不造成歧义的情况下可以简写为d(v)、N(v)）来定义点v的度数和点v的邻点集合。对于图G，分别用V(G)、E(G)、Δ(G)、δ(G)和g(G)来定义它的点集、边集、最大度、最小度和围长（图G中最小圈的长度）。将平面图嵌入平面后，用F(G)表示其面集，一个k+-点（或k--点）v表示点v的度数至少为k（或至多为k）。类似的，用dG(f)表示面f的度数，一个k+-面（或k--面）f表示点f的度数至少为k（或至多为k）。

图G的一个正常k-染色指的是从点集V(G)到颜色集{1，2，...，k}的映射c，使得图G中任意相邻的两点均不同色。用c(v)定义点v的颜色，用Ci(v)定义在N(v)中出现过i次的颜色所构成的集合。

图G的最大平均度一般记作mad(G)，定义为

图的frugal-染色首先由Hind等人在文献［2］中提出。在图G的一个点染色c中，如果每种颜色在点v的邻点中至多出现k-1次，就称点v是k-frugal的。如果图G中每个点都是k-frugal的，就称图G是k-frugal可染的，这个染色称作图G的k-frugal 染色。图G的kfrugal色数，记作χk(G)，指的是使图G满足k-frugal可染所需的最少的颜色数量。由定义易知，χk(G)≥

图的frugal-染色可以推广到列表染色上。设L为一个函数，它将图G中的每个点v都映射到一个由一些正整数构成的集合L(v)上，L(v)称作点v的列表。如果一个染色c：V→N满足c(v)∈L(v)对于所有v∈V都成立，就称这个染色为图G关于L的列表染色，或L-染色，并且称图G是L-可染的。如果图G中每个点的列表长度均满足|L(v)|=l，就称这个列表为图G的l-列表。如果对于任意l-列表L，图G都是k-frugalL-可染的，则满足这个条件的最小正整数l就称作图G的k-frugal 列表色数，记作chk(G)。

图G的lineark-染色是图的一种特殊的正常k-染色。linear染色的定义是由Yuster［3］首先提出的，要求图G中由任意两种颜色导出的子图，均为若干条内部不相交的路。图G的linear-色数，记作lc(G)，指的是使图G满足lineark-染色所需要的最小整数k。

显然，一个linear染色必定为3-frugal染色，但是反过来并不一定成立，因为linear染色中不允许双色圈的存在。更多关于linear染色的结果参见文献［4-9］。

图G的2-distancek-染色是图的另一种特殊的正常k-染色。2-distance染色的定义是由Wegner［10］首先提出的，要求图G中距离小于等于2的两个点均不同色。图G的2-distance-色数，指的是使图G满足2-distancek-染色所需要的最小整数k。

显然，2-distance染色的定义2-frugal染色的定义相同。更多关于2-distance染色的结果参见文献［11-24］。

关于一般的k-frugal染色，Amini等人在文献［25］中证明了对于任意k≥1，平面图G都满足

1 主要结论

下面讨论稀疏图的k-frugal列表染色，并得出如下结论。

2 定理1.1的证明

下面首先证明图G的一些结构，然后通过Discharging的方法来证明这个结论。

引理2.1.δ(G)≥2。

证明：反证法，假设图G含有一个1-点v。由图G的定义知，G-v有一个k-frugalL-染色c。设NG(v)=u，此时若想把染色扩充到图G上，点v禁用的颜色为c(u)以及在NG(u)中出现过k-1 次的颜色（即Ck-1(u)）。因此禁用的颜色至多为

因此，可以将染色扩充到图G上，矛盾。

由图G的定义知，G-v有一个k-frugalL-染色c。此时若想把染色扩充到图G上，点v禁用的颜色为诸c(vi)以及在NG(vi)中出现过k-1 次的颜色（即Ck-1(vi)）。因此禁用的颜色至多为

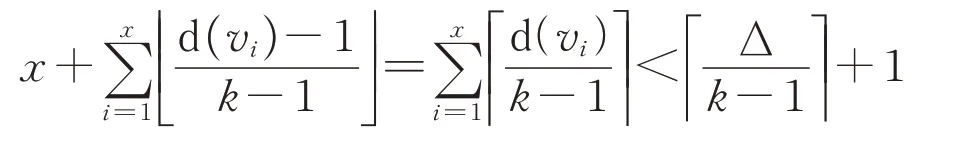
这样就可以将染色扩充到图G上，矛盾。

为了方便证明，下面给出一些定义。

下面通过Discharging的方法得到一个矛盾。给每个点v赋初始权ω(v)=d(v)，因此有

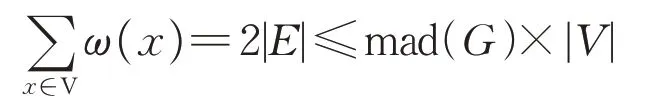
对于每个x∈V，都通过特定的权转移规则（权只能从一个元素转移到另一个元素，故总和不变），得到一个新权ω*(x)，因为在权转移的过程中总和不变，所以仍有

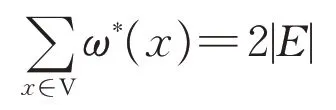
如果在权转移后，得到ω*(x)＞mad(G)对于所有x∈V均成立，则有

这样就得到一个矛盾，从而定理得证。

下面给出权转移规则，Discharging 规则：

综上，得到了一个矛盾，定理得证。

3 定理1.2的证明

下面首先证明图G的一些结构，然后通过discharging的方法来证明这个结论。

引理3.1.δ(G)≥2。

证明：证明方法与引理2.1相同。

引理3.2.G中不含与3--点相邻的2-点。

证明：假设定理不成立，G中存在一个2-点v，且其与一个3--点u相邻。由于图G为极小反例，G-v有一个k-frugalL-染色c。设NG(v)={u，w}，则v禁用的颜色为c(u)，c(w)以及在NG(w)中出现过k-1次的颜色（i.e.Ck-1(w)），所以点v禁用的颜色至多为

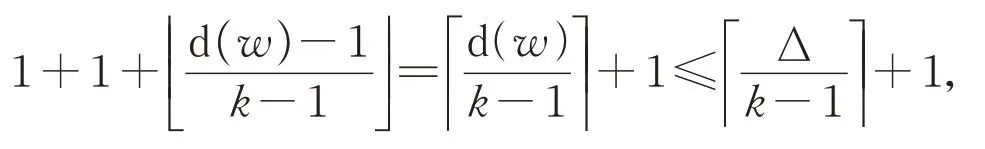
因此，可以将染色c扩充到图G上，矛盾。

引理3.3.G中不含与3个2-点相邻的4-点。

证明：假设定理不成立，G中含有一个4-点v，且其与3个2-点x，y，z相邻。设x1，y1，z1分别为x，y，z的另一个邻点，v1为v的第4个邻点。由于G为极小反例，G-{v，x，y，z} 有 一 个k-frugalL-染 色c。设 点w∈{v，x，y，z}，则w禁用的颜色为c(w1)以及在NG(w1)出现过k-1次的颜色（i.e.Ck-1(w1)），因此点w禁用的颜色为

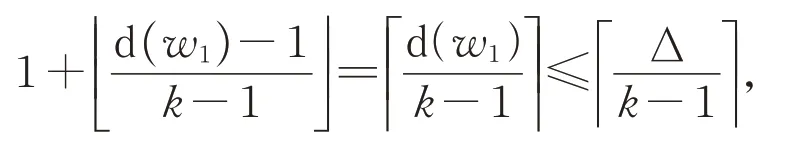
设L*(w)=L(w)({c(w1)}∪Ck-1(w1))，则|L*(w)|≥2，其中，w∈{v，x，y，z}。

首先用c(x)∈L*(x){c(v1)}中的颜色染x，用c(v)∈L*(v){c(x)} 中的颜色染v，用c(y)∈L*(y){c(v)} 中的颜色染y，用c(z)∈L*(z){c(v)}中的颜色染z。容易验证这是图G的一个k-frugalL-染色，矛盾。

引理3.4.G中不含与5个2-点相邻的5-点。

证明：假设定理不成立，G中含有一个5-点v，且NG(v)={x1，x2，…，x5}，dG(xi)=2，yi为xi的另一个邻点（其中i=1，2，…，5）。由于G为极小反例，G{v，x1，x2，…，x5} 有一个k-frugalL-染色c。∀1 ≤i≤5，点xi禁用的颜色为c(yi)和在NG(yi)中出现过k-1 次的颜色（i.e.Ck-1(yi)）。设L*(xi)=L(xi)({c(yi)}∪Ck-1(yi))，易得|L*(xi)|≥对于点v，易得

下面将染色c扩充到图G上。

首先用L*(x1)中的颜色染x1，这个颜色记作a；然后用L*(x2){a}中的颜色染x2，这个颜色记作c(x2)；用L*(v){a，c(x2) }中的颜色染v，这个颜色记作b；最后用L*(xi){b}中的颜色染xi，其中i=3，4，5。容易验证当c(x3)=c(x4)=c(x5)=a和c(x3)=c(x4)=c(x5)=c(x2)均不成立的时候，这个染色为图G的k-frugalL-染色。不失一般性，假定L*(xi)={a，b}且c(xi)=a对于i=3，4，5均成立。

如果L*(x1)≠{a，b}，那么可以用L*(x1){a}中的颜色给x1重新染色，容易验证这是图G的k-frugalL-染色。

下面假设L*(x1)={a，b}。重新给x1和x5染上颜色b，用c(v)∈L(v){a，b}中的颜色重新染v，用L*(x2){c(v)}中的颜色重新染x2，容易验证这是图G的一个k-frugalL-染色，矛盾。

接下来通过discharging的方法来获得一个矛盾，首先给每个点v赋初始权ω(v)=d(v)，设权转移后得到的新权围ω*(v)。

下面给出权转移规则，每个4+-点v转移到相邻的2-点。

下面来验证ω*(x)≥3对于所有x∈V均成立。

设v为一个k-点。

如果k=3，由引理3.2，3点之不与2-点相邻，则ω(v)≥3。

如果k=2，由引理3.2，2-点只能与4+-点相邻，则

综上，得到了一个矛盾，定理得证。

4 定理1.3的证明

下面首先证明图G的一些结构，然后通过discharging的方法来证明这个结论。

引理4.1.δ(G)≥2。

证明：证明方法与引理2.1相同。

证明：证明方法与引理2.2相同。

引理4.3.若v为2-点 且NG(v)={u，w}，d(u)≤d(w)，则d(u)≥2(k-1)+1 ≥7。

证明：假设d(u)≤2(k-1)，带入引理4.2，得d(w)＞Δ，矛盾。

引理4.4.若v为3-点，NG(v)={x，y，z}，且d(x)≤d(y)≤d(z)，则d(z)≥d(y)≥k≥4。

证明：假设d(y)≤k-1，带入引理4.2，得d(z)＞Δ，矛盾。

引理4.5.不存在与6个2-点相邻的7-点。

证明：设v为一个7-点，NG(v)={x1，x2，x3，x4，x5，x6，u}，其中d(xi)=2，NG(xi)={v，yi}（i=1，2，…，6）。

由图G的极小性，图G-{v，x1，x2，x3，x4，x5，x6}有一个k-frugalL-染色c。此时点v被禁用的颜色为c(u)以及在NG(u)中出现k-1次的颜色。因此点v被禁用的颜色至多为

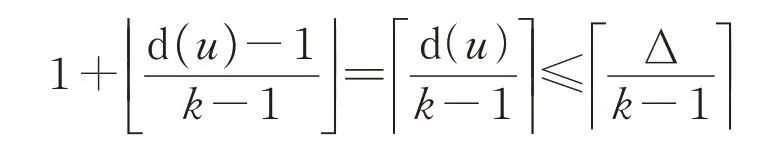
设点v的可用颜色集为L*(v)，则|L*(v)|≥3。

同理可得

点xi∈{x1，x2，x3，x4，x5，x6}的可用颜色集为|L*(xi)|≥3。

下面将这个染色c扩充到图G上。

给x1染颜色c1∈L*(x1){c(u)}，给x2染颜色c2∈L*(x2){c(u)，c1}，给v染颜色c3∈L*(v){c1，c2}。

给x3染颜色a1∈L*(x3){c3}，给x4染颜色b1∈L*(x4){c3，a1}。

给x5染颜色a2∈L*(x5){c3}，给x6染颜色b2∈L*(x6){c3，a2}。

因此，a1≠b1，a2≠b2，c1≠c(u)，c2≠c(u)。

集合c1，c2，a1，b1，a2，b2，c(u)中同种颜色至多出现3次，因此得到的染色为图G的一个k-frugalL-染色，矛盾。

引理4.6.设k为正整数，8 ≤k≤9，则不存在与k个2-点相邻的k-点。

证明：这里不妨假设k=9，因为只要k=9成立，k=8的情况类似可证。

设点v为一个9-点，且与9 个2-点相邻。NG(v)={x1，x2，…，x9}，yi为点xi异于点v的另一个邻点。由G的极小性，图G-{v，x1，x2，…，x9}有一个k-frugalL-染色c。

此时点xi被禁用的颜色为c(yi)以及在NG(yi)中出现k-1次的颜色，点v可以染其本身列表中的任意一种颜色。

设点v的可用颜色集为L*(v)，点xi的可用颜色集为L*(xi)（其 中i=1，2，…，9），则|L*(v)|=|L(v)|≥1+3=4，|L*(xi)|≥3。

下面采用如下方式将这个染色c扩充到原图G上。

给x1染c(x1)∈L*(x1)，

给x2染c(x2)∈L*(x2){c(x1)}，

给x3染c(x3)∈L*(x3){c(x1)，c(x2)}，

给x4染c(x4)∈L*(x4)，

给x5染c(x5)∈L*(x5){c(x4)}，

给x6染c(x6)∈L*(x6){c(x4)，c(x5)}，

给x7染c(x7)∈L*(x7)，

给x8染c(x8)∈L*(x8){c(x7)}，

给x9染c(x9)∈L*(x9){c(x7)，c(x8)}，

此时，点x1，x2，x3的颜色互不相同，点x4，x5，x6的颜色互不相同，点x7，x8，x9的颜色互不相同。

设S=，则3 ≤|S|≤9。

如果L(v)S≠∅，给点v染c(v)∈L(v)S，就可以把这个染色c扩充到图G上，矛盾。

下面设L(v)⊆S，对k进行分类讨论。

情况1.当k=4 时，|L*(v)|=|L(v)|=

此时L(v)中必然存在3种颜色，这3种颜色在S中出现的次数均小于等于1。因为如果只有两种颜色在S中出现不超过一次的话，可以推出S≥4×2+2×1=10，矛盾。

而且，此时必然有Ck-1(v)=C3(v)≤1，因为如果|Ck-1(v)|≥2，可以推出S≥2×3+4×1=10，矛盾。

此时不妨设c(xi)∈L(v)∩C1(v)，首先擦掉xi的颜色，然后给点v染c(xi)，最后用集合L*(xi)[{c(xi) }∪C3(v) ]中的染色给点xi染色，即可将染色扩充到图G上。

情况2.当k≥5 时，|L*(v)|=|L(v)|=

根据前边的染色方法，得知∀c∈L(v)，颜色c在集合S中出现的次数不超过3，即C4(v)=∅。

此时集合L(v)中至多有两种颜色在S中出现的次数等于3（不妨设这两种颜色为{1，2}），因为如果有3种颜色在S中出现的次数等于3，则可以推出|S|≥3×3+1×1=10，矛盾。

因此，L(v)中总有一种颜色，其在S中出现的次数小于等于2，不妨设这个颜色为{3}。

集合S中至多有两个点颜色为3，不妨设为{vi，vj}，首先擦掉这两个点的颜色，给点v染颜色3，然后给点vi染集合L*(vi){1，3}中的颜色，给点vj染集合L*(vj){2，3}中的颜色，容易验证此时染色满足5-frugal 的条件，因此可以将这个染色扩充到图G上。矛盾。

为了方便下列引理的证明，给出几个定义。若一个3-点与3个4+-点相邻，就称其为重3-点，反之称为轻3-点。若一个8-点与7个2-点和一个重3-点相邻，就称其为轻8-点。

引理4.7.不存在与7个2-点和一个轻3-点相邻的8-点。

下面将染色c扩充到原图G上。

给x8染c(x8)∈L*(x8)，

给x1染c(x1)∈L*(x1){c(x8)}，

给x2染c(x2)∈L*(x2){c(x8)，c(x1)}，

给x3染c(x3)∈L*(x3)，

给x4染c(x4)∈L*(x4){c(x3)}，

给x5染c(x5)∈L*(x5){c(x3)，c(x4)}，

给x6染c(x6)∈L*(x6)，

给x7染c(x7)∈L*(x7){c(x6)}，

此时，点x8，x1，x2的颜色互不相同，点x3，x4，x5的颜色互不相同，点x6，x7的颜色互不相同。

设S=，则3 ≤|S|≤8。

如果L(v)S≠∅，令c(v)∈L(v)S，就可以把这个染色扩充到图G上，矛盾。

下面不妨设L(v)⊆S，对k进行分类讨论

情况1.当k=4 时，|L*(v)|=|L(v)|=≥3+3=6从而|S|≥L(v)≥6。

此时L(v)中必然存在3种颜色，这3种颜色在S中出现的次数均小于等于1。因为如果只有两种颜色在S中出现不超过一次的话，可以推出S≥4×2+2×1=10，矛盾。

而且，此时必然有Ck-1(v)=C3(v)≤1，因为如果|Ck-1(v)|≥2，可以推出S≥2×3+4×1=10，矛盾。

此时不妨设c(xi)∈L(v)∩C1(v)，首先擦掉xi的颜色，然后给点v染c(xi)，最后用集合L*(xi)[{c(xi) }∪C3(v) ]中的染色给点xi染色，即可将染色扩充到图G上。

情况2.当k≥5 时，|L*(v)|=|L(v)|=≥4，从而|S|≥L(v)≥4。

根据前边的染色方法，得知∀c∈L(v)，颜色c在集合S中出现的次数不超过3，即C4(v)=∅。

此时集合L(v)中至多有两种颜色在S中出现的次数等于3（不妨设这两种颜色为{1，2}），因为如果有3种颜色在S中出现的次数等于3，则可以推出|S|≥3×3+1×1=10，矛盾。

由于L(v){1，2，c(x8)}≠∅，从该集合中任取一个颜色c1，则集合S中至多有两个点的颜色为c1，不妨设存在两个点的颜色为c1（若只有一个点颜色为c1，证明方法类似），且这两个点均不为x8。设这两个点为{vi，vj}。首先擦掉这两个点的颜色，给点v染颜色c1，然后给点vi染集合L*(vi){c1，1}中的颜色，给点vj染集合L*(vj){c1，2}中的颜色，容易验证此时染色满足5-frugal的条件，因此可以将这个染色扩充到图G上。矛盾。

引理4.8.不存在与两个轻8-点相邻的3-点。

证明：由定义，得知与轻8-点相邻的3-点一定是重3-点。

上述3种染色方案中点v使用的列表均不完全相同，因此cx(v)，cy(v)，cz(v)这3种颜色不可能完全相同，所以总可以找到两个方案，不妨设为cx，cy，满足cx(v)≠cy(v)，这里不妨设cx(v)=a，cy(v)=b。

容易验证此时得到的染色为原图的一个k-frugalL-染色，因此可以将染色c扩充到图G上，矛盾。

这样就通过discharging的方法来获得一个矛盾，首先给每个点v赋初始权ω(v)=d(v)，设权转移后得到的新权为ω*(v)。

下面给出权转移规则：

如果k=8，由引理4.6，点v周围至多存在7个2-点，下面分两种情况讨论。

这样就得到一个矛盾，定理得证。

作者贡献声明：

房启明：提出研究问题，设计研究方案，起草论文；

张莉：对发表文章作最后的审阅和定稿，并在研究的过程中提出诸多启发性观点。