“双碳”目标下绿色双层投资组合研究
徐凤敏,刘文玲,李雪鹏,景 奎
(西安交通大学 a.经济与金融学院;b.马克思主义学院,陕西 西安 710049)
一、引 言
马科维茨均值方差模型作为现代金融理论的基石,最早将资产随机收益的一阶和二阶信息作为收益和风险的客观表达,并由此构建量化模型[1]。此后在投资组合模型纳入并修正传统财务和风险指标成为贯穿投资组合研究的一条重要脉络,在实务界和学术界都取得了丰硕的成果。近年来随着低碳经济发展理念在全球范围的传播演进,越来越多的投资者出于监管需求或者道德准则倾向于在投资中纳入环境、社会责任和综合治理等非财务因素,即ESG(Environment,Social and Governance)投资[2]。
2021年是碳中和发展的元年,绿色金融市场规模的增加令专注投资组合理论和ESG投资理念的整合策略成为研究热点(1)GISA:Global sustainable investment review 2018。。研究者早在21世纪初就尝试在投资组合模型中纳入非财务指标。按照笔者分类,文献可以归纳为两个脉络,即是否基于整合策略设计投资组合模型,见表1。整合策略最显著的特点是在传统投资组合决策中系统地纳入ESG或者其他非财务因素(2)CFA协会:中国的ESG整合:实践指导和案例研究。。而区别于系统性,负面剔除、正面筛选以及ESG倾斜都是基于投资人的先验信息不假思索地对资产池进行排他性筛选、剔除或者倾斜,但在模型层面并没有进行显著改良[3-5]。虽然负面剔除策略是业界应用的主流,但是据GISA预测,未来十年ESG整合策略的市场规模将会彻底超过非整合策略。
当前基于整合策略的绿色投资组合模型可以分为四类。第一类是基于多目标框架的ESG投资组合模型。Chen等运用数据包络分析框架处理ESG因素,并将其嵌入到均值方差模型,提出了三阶段绿色投资框架,其主模型是关于收益、风险和ESG评价的多目标优化模型[6]。Alessandrini等认为正向或负面筛选策略虽然会改善投资组合的ESG质量,但是会导致多样性不足以及过多的风险暴露[7]。在多样性和风险暴露约束下,Alessandrini提出了极大化ESG绩效的投资组合模型。实证结果表明获得组合至少和基准指数相当。Gasser等将ESG得分纳入到投资过程,提出了三目标马科维茨投资组合模型,在大样本求解中依赖最小方差模型构造双重优化过程,即通过构造ESG—风险,以及收益—风险有效前沿得到三维情形的有效前沿曲面[8]。Bilbao-Terol等以共同基金为研究对象,以买卖单位为变量构建了包含ESG目标的多目标的绿色投资组合模型,并设计两步法求得了ε-约束下的近似最优解[9]。第二类是在经典投资组合理论中考虑ESG约束。Herzel等在指数追踪问题中考虑E、S和G三个维度的线性不等式约束,构造了绿色指数追踪模型[10]。Liagkouras等在稀疏均值方差框架下考虑了ESG等式约束,并结合预处理筛选不符合资质的非绿资产。第三类从预期效用理论出发,考虑投资者的绿色效用[11]。Chen等认为投资组合构建中要考虑投资者的可持续价值以达到alpha收益和可持续目标的协调统一[12]。Henriksson等将上市公司按照ESG表现分为优差两组,并由此构造新型ESG因子用以构造投资组合,结果表明该方案倾向配置ESG表现良好的公司,远离ESG业绩差的公司[13]。Schmidt在均值方差模型的目标函数中增加了投资者的绿色效用函数,并用ESG评分和资产收益的偏相关系数修正了风险测度,此外他还定义了带有ESG因子的夏普比率,用以确定最优的ESG偏好参数[14]。此外,一些投资者在完整投资过程中纳入ESG因素。Ballestero等依赖于资产是否符合ESG标准的判断,权衡ESG资产收益效用目标和普通资产收益效用目标,提出了道德—财务双目标的投资组合选择模型[15]。其中ESG属性没有体现在模型中,而是以先验信息的方式嵌入到资产分类。Tsai等从四个评价准则、四个备选方案以及多个底层指标入手,构建了社会责任基金选择的整合框架,其在模型中嵌入了结合DEMATEL方法、分析网络过程和0-1目标规划方法用以最优决策ESG投资组合[16]。Nagy等提出了三种ESG倾斜策略,分别是纳入最坏表现ESG、ESG正向倾斜以及ESG动量策略,结果显示ESG动量具有最佳表现,减持低评级ESG企业可以增强投资组合收益,但是高评级ESG对收益的作用受市场周期波动作用[3]。
现有投资组合模型虽然从约束、目标以及效用函数的角度建立了与ESG投资的联系,但仍然存在两个重要问题需要加以解决。第一,现有整合模型很少考虑组合的规模。随着金融市场的规模日益扩大,以及可供投资产品的爆发式增长,投资者需要控制投资组合成分标的数量,即投资品类,以限制可能带来的额外管理费用和交易成本[17-19]。第二,无论哪一类整合策略模型,都需要引入额外的参数。比如,在约束中考虑ESG因素需要投资者决策最优的ESG配置目标,在目标中考虑ESG效用需要投资者决策对ESG的偏好。在实践中做出类似决策常依赖投资者、基金经理的技术能力或者朴素的问卷调查。
已有学者尝试利用双层规划解决投资组合中的参数估计问题。Stoilov等使用双层规划模型估计风险厌恶系数,其中上层目标是风险调整后收益,下层是只有预算约束的投资组合模型,利用下层问题的最优性条件可以推导参数的闭式解[20]。Stoilov等构造了一个双层投资组合模型用以选择最优的VaR(Value at Risk),其中下层问题是经典的均值方差模型,上层问题是正态分布假定下VaR的表达式[21]。Kalashnikov等将Stoilov等提出模型的上层目标替换为最大化预期收益,并设计混合整数线性规划算法求解最大收益下的风险厌恶系数[22]。Utz等利用逆优化思想构造了一类双层投资组合参数估计模型,并借助非支配有效前沿曲面计算投资者关于风险的厌恶系数[23]。Gonzlez-Díaz等应用双层投资组合模型研究做市商的最优费率设置,在上层问题中做市商控制交易费率获得最大收益,下层问题中投资者得到CVaR(Conditional Value at Risk)度量下的最优投资组合[24]。Jing等为估计稀疏投资组合的稀疏度以及预期收益目标,提出了双层投资组合参数估计模型,其中上层极大化夏普比率,下层为稀疏均值方差模型[25]。基于上述模型,徐凤敏等为双层投资组合模型设计了无导数算法,其中下层问题通过三块ADMM算法高效求解[26]。
针对当前ESG投资组合构建中存在的现实困境,本文利用双层参数规划思想构建绿色投资组合模型。具体而言在下层问题构造含ESG效用的绿色投资组合模型,决策变量是组合权重;上层问题是关于给定基准和绿色组合的极小化误差函数,决策变量是两类风险厌恶系数以及投资组合稀疏位置。在理论层面,本文给出了简单约束下投资组合和参数的闭式解,并在一般条件下通过下层问题的KKT条件将双层规划转化为混合整数二次规划问题。在实务层面,本文提出的双层投资组合模型可以为投资者提供最优参数选择下的投资组合。实证中,我们给出了两类具体的应用:第一,给定市场指数或绿色指数作为基准,本文提出的模型利用逆优化思想反推出不同基准对ESG的偏好,进而对基准指数绿化程度进行横向和纵向的总体评估;第二,基金经理可以借助本模型ESG的偏好自适应构造最优的绿色指数型基金,进而避免复杂的参数决策过程。

表1 ESG投资模型分类和比较
二、模型构建
已有绿色投资组合模型多是在马科维茨均值方差模型基础上通过引入ESG目标、ESG约束或ESG效用等手段纳入ESG因素。本节根据双层规划的思想构造绿色投资组合模型,其中上层决策变量是投资者绿色效用函数中关于收益和ESG的风险厌恶系数,以及组合的稀疏位置;下层变量是投资组合权重。
(一)基于绿色效用的投资组合模型
对由n个资产构成的投资组合,根据冯·诺依曼-摩根斯坦效用函数理论,经典的马科维茨投资组合模型下风险厌恶型投资者的效用函数可以表征为关于风险和收益的二次函数:
U(x)=λ1μTx-xTCx
(1)
其中μTx和xTCx分别是投资组合的预期收益和方差度量的风险,x∈n是投资组合权重向量,μ∈n是投资组合资产的预期收益向量,C∈n×n是资产间的协方差矩阵,λ1是投资者对于收益的容忍程度,以下统称为风险厌恶系数。当λ1≥0时,投资组合预期收益的增加会带来正的效用,当λ1≤0时,投资组合的预期收益的增加会降低总体效用(3)在后文中,我们并不假设风险厌恶系数总是正的,因为对于某些标的组合,尤其是被动型基金,收益能力并不是首要的。。
对于绿色投资者,在期望效用函数中考虑线性ESG效用成分[5,8,17],此时绿色投资者的效用:

图1 绿色均值方差模型——风格定义注:第1象限中的(λ1,λ2),ER越大投资者对ESG的重视程度越高;第3象限中的(λ1,λ2),ER越大投资者对ESG的排斥程度越高;第2象限中的(λ1,λ2),λ2越大投资者对ESG的重视程度越高;第4象限中的(λ1,λ2),λ2越小投资者对ESG的偏好程度越低。
U1(x)=U1(x)-λ2gTx
(2)
其中λ2为关于投资组合ESG水平的容忍程度,以下统称为ESG偏好系数,g∈n是投资组合资产的ESG得分向量。在实际中考虑投资组合上下界约束:
Ω0={x|eTx=1,l≤x≤u}
(3)
其中e∈n是全一向量,l和u分别是投资组合成分的上下界,在本问题中l=0。
在约束条件下极大化投资者的绿色效用,此时投资组合模型:
s.t.x∈Ω
(4)
当Ω=Ω0时,模型(4)被称为绿色均值方差模型[11,16],是一类特殊的二次规划模型。当Ω=n时,模型(4)是考虑投资者绿色效用的无约束优化问题。
图1定义了不同参数空间(λ1,λ2)下模型(4)的投资风格。按照(λ1,λ2)在象限中的位置,参数λ1和λ2的正负体现了投资者的个人偏好,将第1到第4象限中的投资者称为:绿色型投资者,纯绿型投资者,保守型投资者,绿色厌恶型投资者。由此定义参数的相对强度指标ER=|λ2/λ1|,其相对大小体现了不同投资者对收益和ESG水平的关注性强弱。
表2列出模型(4)和一些主流投资组合模型的联系。当λ1→∞时,投资组合关注有最大收益的某几类资产,同理当λ2→∞时,投资组合会优先选择具有最大ESG水平的资产。
以上分析表明,参数(λ1,λ2)的选择不仅影响所获组合的风格,还会影响最终的投资决策。不同需求的投资者可以依据自身收益—风险—ESG追求动态调整模型(4)参数。但凭经验判断或问卷调查得到的参数常会导致投资组合具有显著性差异。

表2 模型(4)和投资组合模型的关系

图2 模型(4)和基准组合的偏差注:x和y轴分别是风险厌恶参数和ESG偏好参数,z轴是基准和绿色组合的二范数(‖x-b‖2)。模型中稀疏度为投资组合规模上限,资产上界为1。资产池为上证50成分股,基准为上证50指数权重,样本为2014年3月到2015年3月,估计方式见实证部分。
当投资者预先设定业绩比较基准时,不妨假设基准投资组合为b∈n。图2给出了(λ1,λ2)取值下,由模型(4)得到的投资组合和基准组合的差别。可以观察到在零点附近随着(λ1,λ2)的变化,投资组合和基准组合的差别会剧烈波动,而当|λ1|或者|λ2|取值较大时,投资者对收益或者ESG水平的偏好或者厌恶会占据主导地位,变化趋于稳定状态。
(二)绿色双层投资组合模型
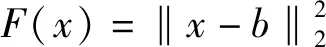
s.t.x∈Ψ1(λ1,λ2,Q),
eTQ≤k,Q∈{0,1}n
(5)
s.t.eTx=1,
Q⊙l≤x≤Q⊙u
(6)
其中,Ψ1(λ1,λ2,Q)是下层问题的最优解集,k是稀疏度,表示投资组合内资产的个数,Q∈n是0-1变量,分量为1表示该资产纳入投资组合,0表示不纳入。模型(5)是一个具有嵌套结构的双层混合整数二次规划问题,其中上层是关于参数(λ1,λ2,Q)的混合整数规划问题。其决策变量包括三方面内容,分别是风险厌恶系数和ESG偏好系数的选择,以及投资组合成分的选择。下层问题(6)是绿色均值方差模型,其中约束由0-1变量Q修正。可以证明该问题一定是NP-Hard[19]。投资者在投资过程面临两个顺序决策,即投资组合的参数选择,以及下层问题的最优组合,两者相互影响。投资者需要在可行空间内做出最优的决策,使得下层问题得到的绿色投资组合和基准组合尽可能趋于一致。文中将双层规划得到的组合称为绿色投资组合。
三、理论分析
通过分析特殊情形下模型(5)显式表达解,并在一般情形下利用子问题的最优性条件将双层问题转化为单层优化问题。
(一)无约束情形
当上下层为无约束优化问题时,可以通过下层问题的最优性条件将双层规划简化为无约束优化问题,进而得到模型(5)在无约束情形的闭式解。
定理1当Ω=n时,模型(5)上层问题最优解为λ=H-1d,此时下层问题最优解:

证明:下层问题的一阶最优性条件:
(7)
代入到上层优化问题,可以得到新的无约束优化问题:
(8)
其中H是对称正定矩阵,此时λ=H-1d,证明完毕。
(二)非稀疏情形
当稀疏度为k=n,此时Q为全一向量,上层问题为无约束优化问题,投资者只需要决策两类偏好。此时可以通过下层问题的最优性条件将双层规划转化为单层的混合整数规划问题。
定理2如果Ω=Ω0={x|eTx=1,l≤x≤u},则模型(5)可以转化为单层规划模型:
s.t.eTx=1;I,P∈{0,1}n
I⊙m≥γ2≥0,P⊙m≥γ3≥0,
2Cx-λ1μ-λ2g+γ1e-γ2+γ3=0,
x≥max{l,u-(1-P)⊙m},
x≤min{u,l+(1-I)⊙m},
x∈n,λ∈2,γ∈3;I,P∈{0,1}n
(9)
其中⊙表示逐点相乘,γ1∈,γ2和γ3∈n,分别是关于预算约束、上下界约束的拉格朗日乘子,I∈n和P∈n是和互补松弛约束相关的0-1变量,m∈是保证互补松弛约束可行的充分大的正数。
证明:考虑下层问题的拉格朗日函数:
L(x|λ,γ)=xTCx-λ1μTx-λ2gTx+γ1(eTx-1)+γ2(l-x)+γ3(x-u)
(10)
引入0-1向量P∈n和I∈n处理互补松弛约束,此时下层问题的最优性条件可以表征为:
x≥max{l,u-(1-P)⊙m},
x≤min{u,l+(1-I)⊙m},
2Cx-λ1μ-λ2g+γ1e-γ2+γ3=0,
I⊙m≥γ2≥0,
P⊙m≥γ3≥0,
eTx=1
(11)
带入最优性条件到上层优化问题,可以得到模型(9),证明完毕。
(三)稀疏约束情形
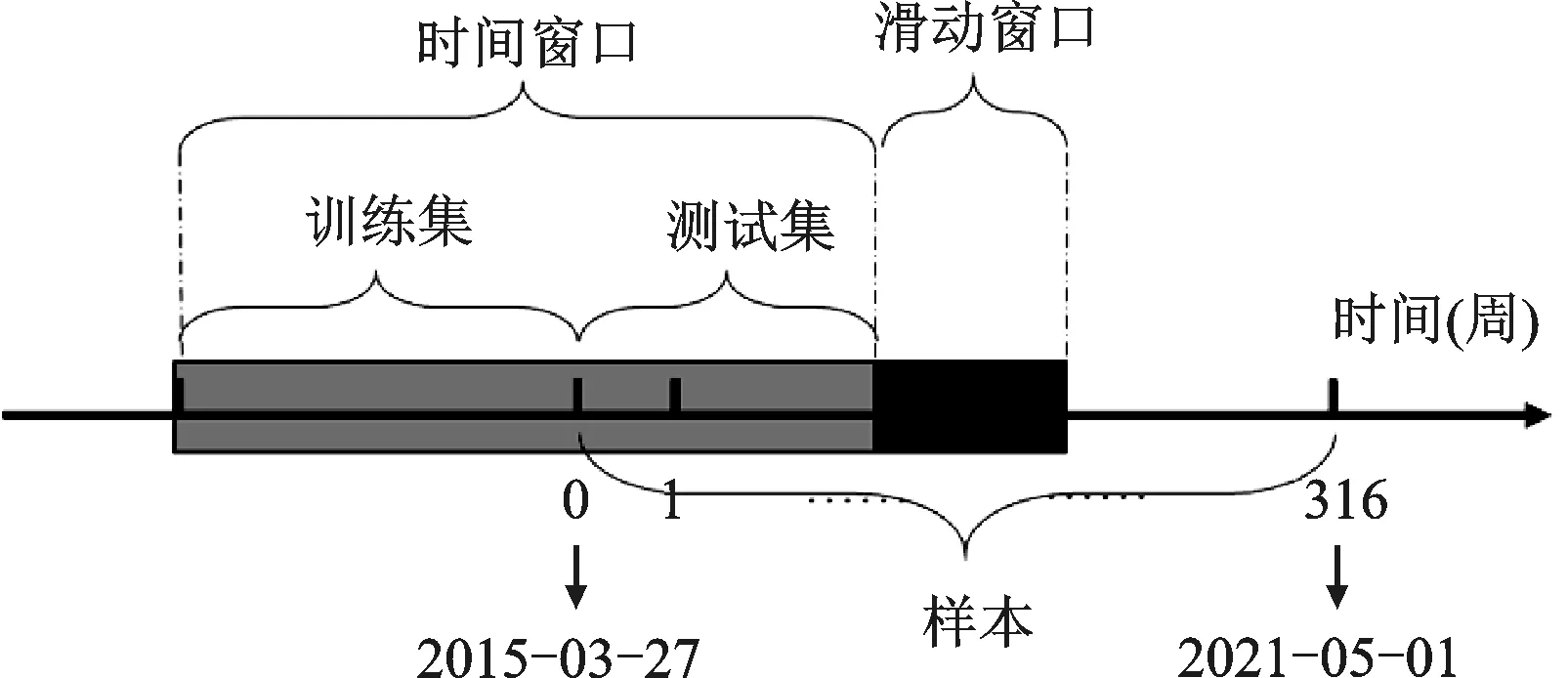
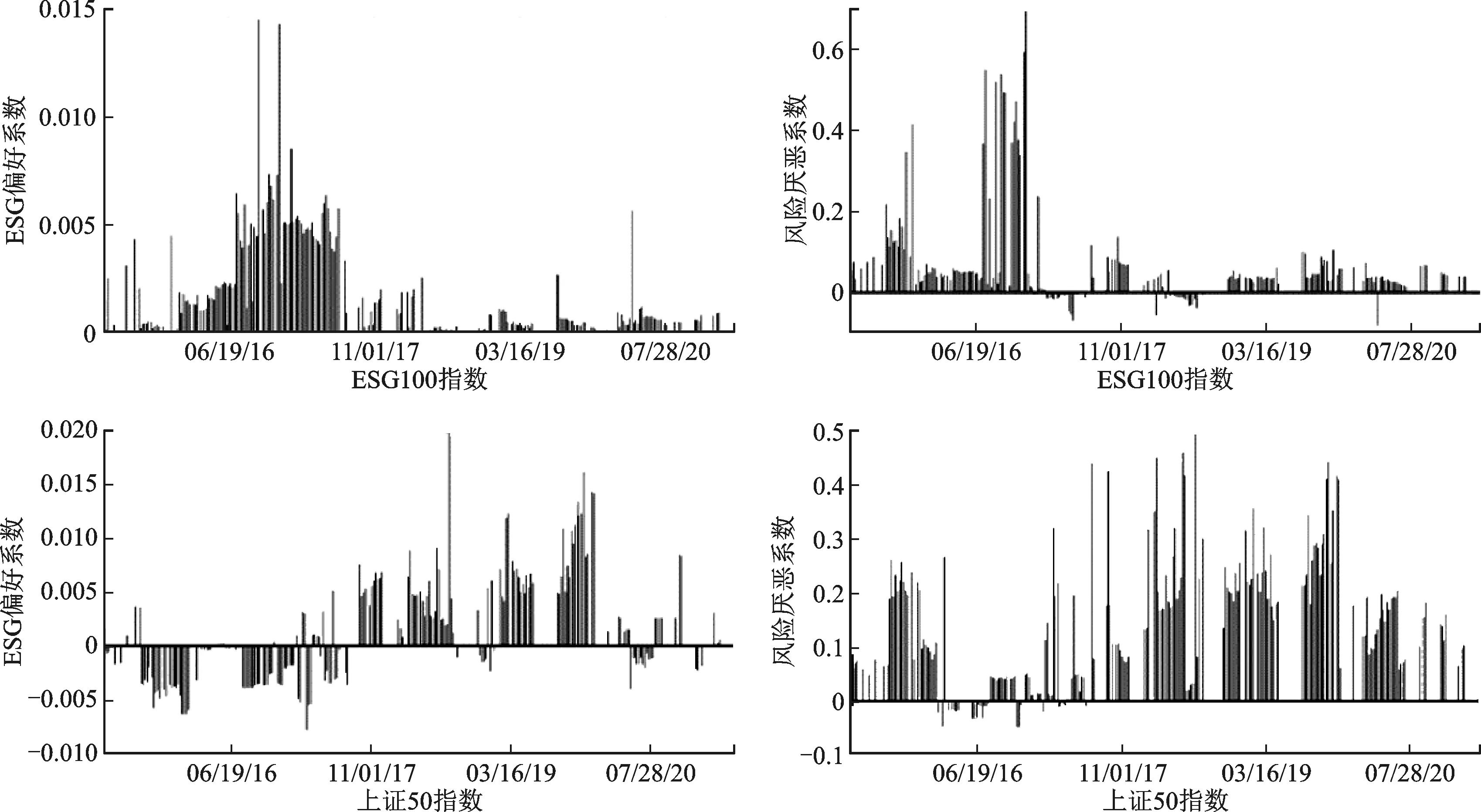
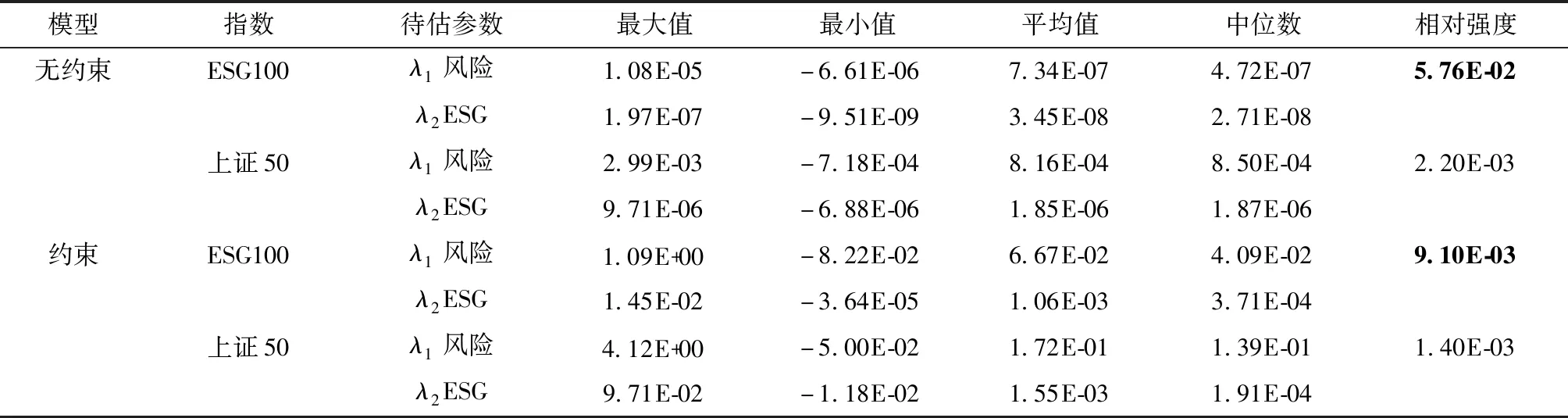
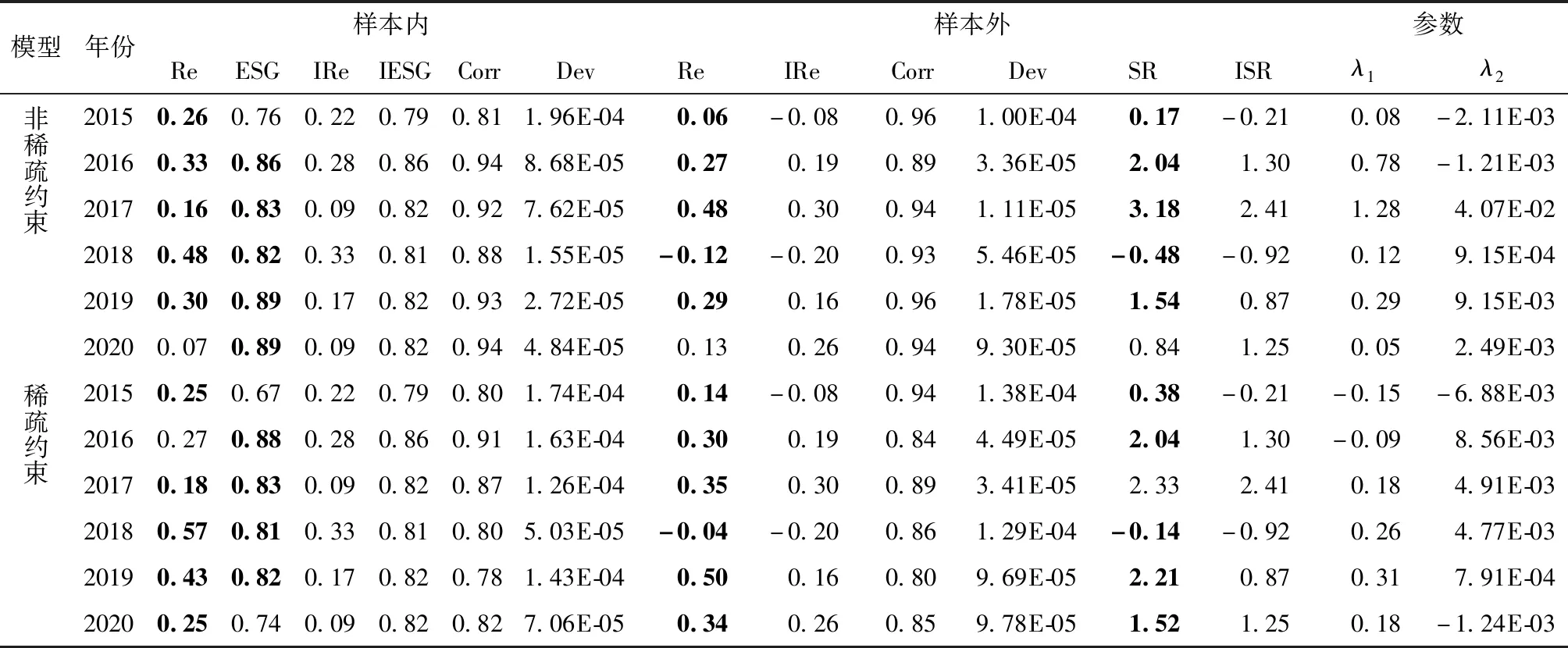
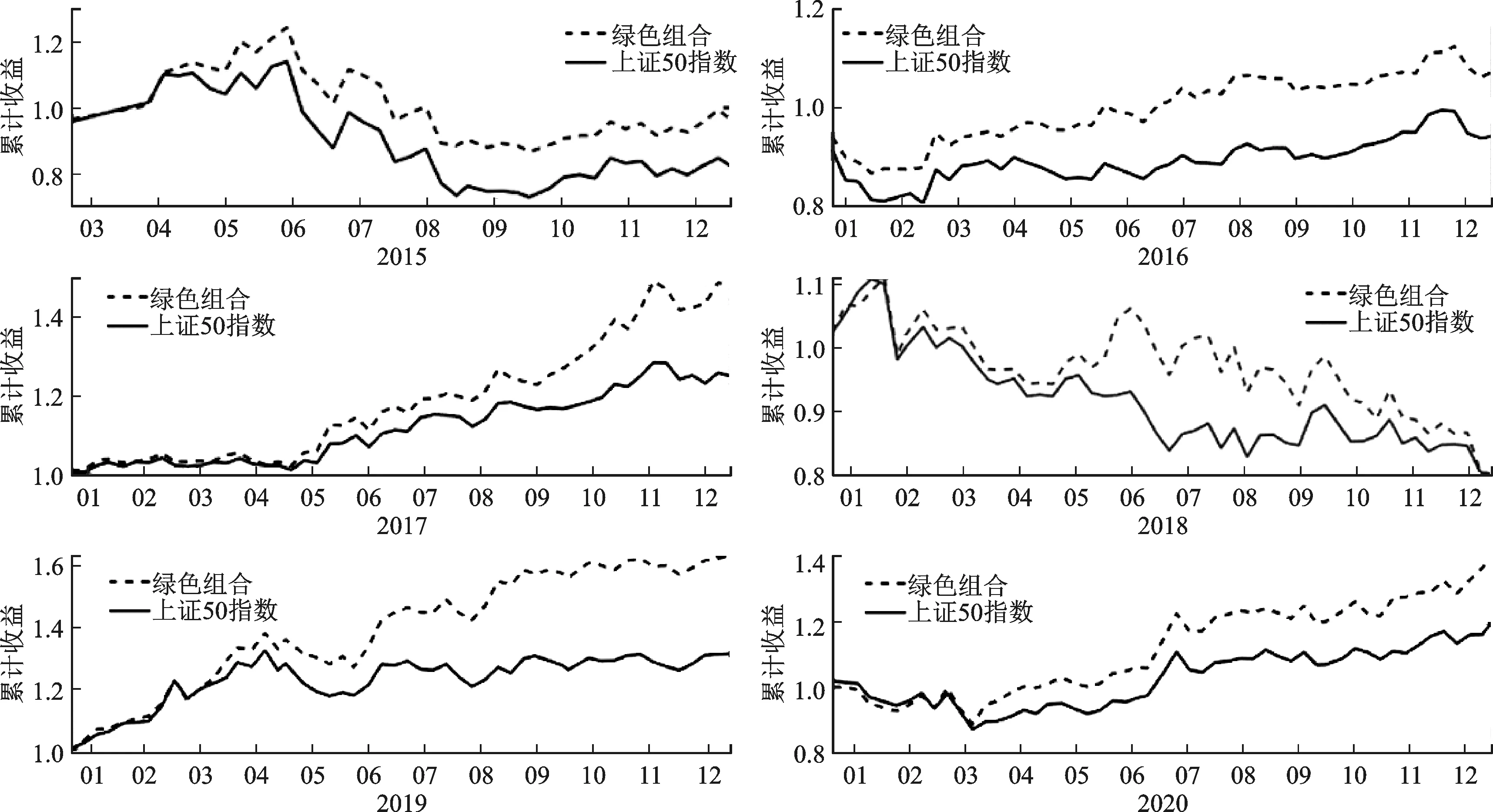
定理3当k s.t.eTx=1,eTQ≤k, I⊙m≥γ2≥0,P⊙m≥γ3≥0, 2Cx-λ1μ-λ2g+γ1e-γ2+γ3=0, x≥max{Q⊙l,Q⊙u-(1-P)⊙m}, x≤min{Q⊙u,Q⊙l+(1-I)⊙m}, x∈n,λ∈2,γ∈3;I,P,Q∈{0,1}n (12) 证明:当上层问题存在稀疏约束时,下层问题的拉格朗日函数: L(x|λ,γ)=xTCx-λ1μTx-λ2gTx+γ1(eTx-1)+γ2(Q⊙l-x)+γ3(x-Q⊙u) (13) 此时KKT(Karush-Kuhn-Tucker)条件为: Q⊙l≤x≤Q⊙u, 2Cx-λ1μ-λ2g+γ1e-γ2+γ3=0, γ2≥0,γ3≥0, γ2⊙(Q⊙l-x)=0,γ3⊙(Q⊙u-x)=0, eTx=1 (14) 引入0-1向量P∈n和I∈n处理互补松弛约束γ2⊙(Q⊙l-x)=0,γ3⊙(Q⊙u-x)=0,则有: I⊙m≥γ2≥0, P⊙m≥γ3≥0, Q⊙u-x≤(1-P)⊙m, Q⊙l-x≥-(1-I)⊙m (15) 整理条件(14)和(15)可以得到模型(12),证明完毕。 模型(9)和模型(12)是一类带有0-1变量的混合整数二次规划问题,可以将模型(5)视为投资者不限制资产个数的特殊形式。目前市场上流行的商业求解器,如CPLEX、GUROBI可以用于求解此类问题。 通过采用中国A股市场价格和ESG数据对上述提出的模型进行实证研究。本文提出的双层投资组合模型有两类重要的应用,其一在于反向推断市场上公开交易指数的ESG偏好系数和风险厌恶系数,进而刻画市场对于资产ESG和收益属性的情绪变化;其二在于可以构造绿色指数型基金。所有数值结果均采用MATLAB R2018b平台上的GUROBI 8.0求解,其中参数保证互补松弛约束成立。对于非稀疏约束情形,根据沪深交易所《证券投资基金业务指引第1号——指数基金开发》(以下称《指引》),投资权重上界选择0.15。对于稀疏模型,为了使得约束问题可行,上界取为0.5。 1.ESG数据 ESG评级体系作为ESG投资发展的基础设施得到了高速发展。当前市场流行的ESG评级体系包括,商道融绿、社会价值投资联盟、富时以及华证评级等。因为华证的ESG评级范围涵盖整个A股市场,按照季度更新,且自2015年持续至今,因此本文中所有ESG评级数据均来自华证评级(Wind)。华证ESG评级自最高的AAA到最低C,一共九个评级区间。本文采用归一化方案将评级映射到[0,1]区间,其中最高一档评分为1,最低一档评分为0。 2.基准指数 中证财通ESG100是以沪深300指数为蓝本选制的ESG指数,也是国内最早发布、最具代表性的ESG指数。本文选择上证50以及中证财通ESG100指数(以下简称ESG100)作为上层目标的绿色和非绿色基准指数。模型中基准指数权重采用训练集内最近一月由平均市值计算得到的权重向量。训练集内新纳入或者剔除的成分不予考虑。 图3 数据集生成方式注:灰色阴影部分为第一个时间窗口,包含测试集和训练集两部分,黑色阴影为滑动窗口,即下一个数据样本需要增删的长度;0表示数据的开始位置,316为数据的终止位置。 3.收益数据 为减少数据估计误差,本文采用2015年3月27日到2021年5月1日ESG100以及上证50成分股的周收益率数据,共计316个交易周,包含431只个股。图3显示了静态实验和动态试验中数据集的生成方式。对于静态实验,测试集长度由投资者遵照投资时限确定,训练集长度为104周。参照基准指数的成分股列表,利用训练集内对应历史周收益估计资产的预期收益、协方差以及ESG评分。训练集内停牌、ST的股票均予以剔除。考虑到ESG按照季度更新,如果最新的评级数据存在,则不做剔除操作。对于动态实验,在每一个时间窗口下采用静态方式计算投资组合,同时按照滑动窗口大小,删除训练集内同样长度的旧样本,并按照时间顺序平移整个时间窗口。在之后的实证中,令滑动窗口和测试集窗口保持同等长度。 4.评价准则 引入皮尔逊相关系数和下半偏差[17-19]描述绿色投资组合和基准的相似性及追踪误差: (16) 其中rp和rb分别是投资组合和基准的收益率,cov(rp,rb)是投资组合和基准的协方差,σ(rp)和σ(rb)分别是投资组合和基准的标准差。相关系数衡量了投资组合和基准组合的一致性,其值越大则追踪效果越好。下半偏差衡量了投资组合落后于基准部分的L2范数,其值越小表明投资组合相对于基准获得超额收益能力越强。 为度量投资组合业绩表现,引入夏普比率、信息比率以及Omega比率三种评价准则[27-29]: (17) 其中E(rp)和σ(rp)分别是投资组合的预期收益和标准差,rf是无风险收益率,rb是投资组合用于比较的基准。夏普比率描述了投资组合在一段时间内单位风险下的超额收益。信息比率描述了投资组合相对于某一基准下的风险调整收益,表示单位主动风险下的超额回报。Omega比率衡量了投资组合相对于基准的收益损失,体现了收益的高阶矩信息,表示为正向收益和负向收益的比值。三类指标数值越大,则投资组合的业绩表现越好。 本节给出一个数值例子验证绿色双层投资组合模型的有效性。考虑包含十个资产的投资组合,其中资产的预期收益、ESG水平和协方差矩阵(4)收益数据和ESG数据利用模拟方法生成,数量级和周类型数据保持一致。为μ,g和C,见表3。 1.稀疏度选择 随机生成2 000个投资组合作为可能的基准(5)利用matlab内置的随机函数生成0-1之间随机数,并利用归一化方法确保权重为1。,利用模型(5)计算最优参数下2 000个投资组合。图4展示了上层目标函数最优值的频数分布直方图。可以发现引入稀疏约束后,由模型(5)得到的绿色投资组合成分和基准的偏差进一步增大。这点可以由稀疏模型的理论性质解释,即随着投资组合样本内个数的减少,双层规划的诱导集被进一步压缩,造成最优目标函数的下降。如果投资者过于严苛地要求稀疏性,有可能会导致绿色投资组合和基准追踪误差扩大,影响投资组合绩效。实证中我们采用资产池10%到30%之间作为稀疏度的取值范围。 表3 模拟例子:协方差、预期收益率、ESG水平 图4 数值模拟——上层目标函数最优值注:每个直方图对应2 000个绿色投资组合,黑色柱形为模型(8)结果,浅色柱形为模型(5)统计结果;资产上界为0.5,其中模型(5)中稀疏度为3。 2.投资者偏好系数 已有学者从金融市场角度研究其隐含的风险偏好,但现实中仍缺乏估计指数的有效手段[30]。为了检验模型是否可以利用逆优化思想得到最优参数,基于模拟数据事先给定两类风险参数(见表4,第2列),将单层绿色投资组合模型(4)的结果作为模型(5)以及模型(8)的基准。表4考虑图1中不同象限的投资风格以及稀疏要求,给出了十五组模拟实验的结果。 针对非稀疏情形,比较表4中第6~10列的相对误差可以发现,由模型(5)求解得到的绿色投资组合准确还原了基准对应的风险厌恶系数以及ESG偏好系数,上层目标函数在10-14水平接近于零,说明绿色投资组合成分和基准完全一致(6)因为事先给定了最优参数,并由此构造基准组合,因此在理论上最优组合和基准的成分应该完全一致。。当考虑上层目标中的稀疏要求时,此时有效组合对应的最优参数和指数出现偏离,上层目标以及相对误差对比非稀疏情形显著增大。此时得到的投资组合和基准指数相比已经有所不同,对应于图4关于稀疏度选择的结果,随着对稀疏性的强调,有效组合和基准指数的偏离(表4,第10列)将会进一步加大。《指引》中强调了组合的多样性,故在实际中稀疏度的选择不宜过少。 在后面部分,进一步分析本文提出模型的两个应用,其一是利用绿色投资组合度量市场指数蕴含的风险和ESG态度;其二在于利用绿色投资组合构建绿色指数型基金。 表4 投资者偏好系数的估计误差 Utz等利用逆优化思想估计了美股市场上SRI基金和非SRI基金的隐含ESG重要性,结果表明SRI基金会更加关注ESG[23]。本节针对市场上主流的绿色指数(ESG100)以及非绿色指数(上证50),由本文提出的双层规划模型构造绿色投资组合,采用逆优化思想反向估计指数的隐含ESG偏好和风险厌恶系数。换言之,我们将绿色投资组合作为指数的近似组合,用估计的最优参数度量基准的隐含ESG偏好和风险厌恶程度。 本应用考虑上下层无约束和上层无约束两种情形。将下层问题最优投资组合定义为相对于基准的绿色投资组合。令时间窗口长度为104周,滑动窗口为1周,共生成316组绿色投资组合以及相应参数。 (1)针对无约束情形下的绿色投资组合,实证比较ESG100指数和上证50指数的风险厌恶系数,以及ESG偏好系数的变化。 图5中展示了由模型(5)逆优化得到的ESG100指数和上证50指数的隐含ESG偏好系数λ2以及风险厌恶系数λ1。对于ESG100指数,ESG偏好几乎处处为正值,而风险厌恶则随着时间在正负波动。与之形成对比的是上证50指数,其ESG偏好系数并不总是为正的,在2015—2018年间,λ2在正负之间波动,意味着上证50指数并不总是关注ESG水平。随着《关于构建绿色金融体系的指导意见》在2016年9月正式发布,上证50指数作为市场指数的代表越发关注投资中的ESG内容,体现为λ2数值不断达到高点值,而λ1值虽然为正,大小则持续降低。由于指数的成分数量不同无法直接比较,利用第二节定义的相对强度指标(表5,最后一列),可以发现在361个样本中,ESG100指数的相对强度显著大于上证50指数。 图5 无约束:中证财通ESG100指数及上证50指数隐含情绪估计注:左子图为ESG偏好系数,右子图为风险厌恶系数;第一行为ESG100指数,第二行为上证50指数;横轴为时间的域流,纵轴为具体数值。下同。 (2)针对非稀疏约束情形下的绿色投资组合,实验比较了中证财通ESG100指数和上证50指数的风险厌恶系数,以及ESG偏好系数的变化。 图5和图6的区别在于估计隐含参数时考虑了投资组合的约束情形,包括上下界约束以及预算约束,因此更加贴近现实情况。对比两种情况,可以发现ESG100指数的隐含ESG偏好参数为正,代表该指数在构造中始终对ESG投资有正的效用。ESG100指数的隐含ESG偏好在时间上呈现出明显的集聚效应,这一点在无约束情况下没有体现。而上证50指数作为优质大盘股的代表,总体上看对ESG有正向的偏好,但注意到在2018年之前,上证50指数对ESG的偏好并不总是为正。和无约束情形的第二处不同在于ESG100指数的风险厌恶系数总体上为正,说明ESG100指数在实际投资中兼顾了收益性。 图6 约束:中证财通ESG100指数及上证50指数隐含情绪估计 表5列出了图5和图6关于参数的描述性统计结果。由于可供对比的指数样本规模有差距,且成分股不同,直接比较系数的绝对大小缺乏公允。从总体均值的角度分析,无论是绿色指数还是非绿色指数都显示出了对收益和ESG的正向偏好。绿色指数除了关注投资的ESG属性外,同样关注收益性。而对于非绿色指数,除却关于收益性外也关注ESG属性。两者最大的区别在于对ESG和收益属性的关注强度。无论是约束还是无约束情形,相对强度的大小表明ESG100指数相对于上证50指数更偏好资产的绿色因素,换言之,上证50指数相对于ESG100指数更关注收益性。 1.静态投资组合 考虑投资者执行买入持有策略,且投资时限为一年(52周)的静态投资过程。依据模型(5)的计算结果,表6显示了以上证50为基准的绿色投资组合在2015—2020年间的业绩表现,其中黑色加粗表明该指标相对于指数更高。现实中投资组合预期收益及ESG水平的设定依赖于投资者的经验,表6中利用本文提出的稀疏和非稀疏情形的投资组合双层规划模型可以在决策最优参数的条件下,获得符合绿色投资效用的投资组合。在非稀疏情形下可以推测2015—2016年间最优参数下的投资组合属于偏好收益、ESG厌恶类型,即第四象限风格;而在2017—2020年间,则属于第一象限投资风格。稀疏情形下的投资风格分别属于:第三象限(2015),第二象限(2016),第一象限(2017—2019),第四象限(2020)。 表5 风险厌恶系数和ESG偏好系数的描述性统计分析 表6 绿色投资组合描述(上证50指数) 与基准指数的收益(第5列,表6)和ESG水平(第6列,表6)相比,绿色投资组合的预期收益和ESG水平在多数情形下获得了显著的增强。但投资组合的绿色水平绝不仅是越高越好,以2015年为例,投资组合的绿色水平虽然低于指数,但是样本外的平均收益(第9列,表6)和夏普比率(第13列,表6)均超过了同时期基准指数的水平。该结论对于风险厌恶系数同样成立。错误的参数选择可能会导致极端的风险损失,现有的绿色投资组合模型并没有给出参数选择的机制,本文利用双层规划模型给出了估计最优参数的有效方案。 在收益的相关性(平均在0.85以上)和下半追踪误差(数量级在10-4)度量下,表6中投资组合的样本内外保持了高度的一致性。同时,绿色指数的样本外收益以及夏普比率表明,该投资组合显著增强了指数的收益属性,因此由模型(5)得到的绿色投资组合可以用于增强型指数基金的配置。 2.动态投资组合 本部分允许投资者在持有期间按照月度调仓,利用滚动时间窗口的方式由模型(5)构造2015—2020年间动态投资组合。图7和图8分别显示了2015—2020年间以上证50以及ESG100指数为基准构造的绿色投资组合累计收益。 图7 上证50指数和绿色投资组合累积收益比较注:训练集和测试集分别为104周和4周,时间窗口按照4周滚动,即按照月度调仓。以图6中2015年为例,指数的月末权重为基准,利用滚动实验方式计算稀疏模型(5)共12次,图形中虚线累计收益率为绿色投资组合,实线为上证50指数。模型(5)稀疏度为5,上界为0.5。 图8 ESG100指数和绿色投资组合累计收益比较注:训练集和测试集分别为104周和4周,图形中虚线累积收益率为绿色投资组合,实线为ESG指数。模型(5)稀疏度为10,上界为0.2。 可以发现,无论是上证50还是ESG100指数,虚线代表的动态有效组合不仅较好地跟踪了指数的趋势,并且除却ESG100指数在2015年和上证50指数在2018年不及预期,在累计收益率上更是超过指数。本文采用的ESG评级在2015年第一季度上线,受限于底层数据和认知,造成绿色组合在2015年表现不佳的原因可能是机构的评级质量。 表7列出了图7~8中动态投资组合和指数的评价指标,同时引入1/n策略(7)又称为天真策略(naive strategy),即将资金等额分配到投资组合内各个资产,是迄今为止金融市场应用最早的组合配置策略。增加横向对比提高结果的说服力。表中黑色加粗数值表示横向比较中的最佳表现。从平均收益视角(表7,第二列),以上证50指数为基准的绿色投资组合模型在样本外显示出更高的超额收益。绿色组合和基准在ESG属性上保持了一致性,注意到和指数的最大差别出现在2015年,相对误差(8)ESG相对误差的计算方法:|0.77-0.81|/0.81=4.94%。只有4.94%。除却2017和2018年,绿色投资组合在其余时间内最大回撤都是最低的。由于平均收益在2018年为负值,此时夏普比率失效,但是绿色组合在其余年份都获得了最佳表现。按照信息比率(IRR)和Omega比率(OR),绿色组合在4个年份(4/6)超过了1/n策略。对于ESG100指数,除却2015年,绿色组合全面战胜了指数和1/n策略,说明了上述分析的稳健性。图7~8以及表7的数值结果说明了本文提出的双层投资组合模型在实际投资中的有效性,通过决策最优风险厌恶系数和ESG偏好系数得到的绿色投资组合不仅可以稳定地跟踪指数趋势,同时也可以获得超额收益。 表7 动态投资组合样本外表现 “双碳”目标下ESG投资方兴未艾,本文针对预期效用理论中风险和ESG偏好参数难以估计的难题,构建了考虑ESG因素和稀疏约束的双层投资组合模型,为绿色投资组合理论和ESG整合策略的研究提供了新思路。利用双层规划的嵌套决策机制,投资者在上层问题中决策风险厌恶系数和ESG偏好系数,以及投资组合的稀疏位置;在下层问题中则要在最大化绿色效用目标下,根据上层给定参数构建绿色投资组合。在求解层面,针对不同约束情形,利用下层问题的最优性条件将双层规划问题转化为混合整数二次规划,并通过模拟算例验证了所提模型的有效性,即可以在给定基准下估计ESG偏好系数和风险厌恶系数。本文给出该双层投资组合模型在实践中的两类重要应用,即推断资产组合的隐含ESG偏好与风险厌恶情绪,以及构造绿色指数型基金。在ESG偏好与风险偏好推断中,通过验证2015—2021年间编制ESG100指数和上证50指数的341个投资组合,研究发现金融市场上的绿色指数隐含正向的ESG偏好,而非绿指数关于ESG的偏好受环境政策影响;在相对强度指标度量下,绿色指数相比于收益更加偏好资产的绿色属性,换言之非绿色指数对收益属性的偏好胜过绿色属性。在绿色指数型基金构建中,以上证50和ESG100指数为基准构造的静态和动态投资组合在2015—2021年间不仅较好地实现了对基准的追踪,更获得了稳定的超额收益,从夏普比率、信息比率以及Omega比率等指标来看,普遍战胜了基准指数以及1/n策略。 针对上述研究结论,提出以下政策建议: 第一,在“双碳”目标的引导下,公众和机构投资者对绿色投资的关注度和需求与日俱增。对绿色属性有偏好的投资者通常选择持有金融市场上绿色指数的一篮子资产组合作为投资标的。由此带来的关键性问题是:绿色金融指数真的关注绿色么?本文对ESG100指数和上证50指数的隐含ESG偏好和风险厌恶的测算结果表明,按照绿色属性编制的ESG100指数比一般的金融指数更加偏好绿色投资。换言之,投资者持有以绿色金融指数为标的的基金组合会比持有市场组合带来更多的绿色效用。因此,对于市场上专注于绿色投资的散户而言,可以投资某些金融指数编制的指数型基金来支持“双碳”政策,促进产业的绿色升级和转型。当前绿色金融产品缺口较大,对于监管机构,应该加快出台相关政策支持建立基于绿色金融指数的交易型开放式指数基金等金融产品,发挥金融市场的杠杆作用,带动社会存量资金流入绿色生产、转型、创新等领域。 第二,二级市场的投资者倾向于持有多样化的组合分散风险,但是当前金融市场缺乏代表性绿色金融投资者工具,其中的关键性问题在于传统的投资组合理论并没有纳入资产的非财务因素,因而理论和实际存在脱钩。本文构建的绿色双层投资组合模型在传统的投资组合理论中纳入了ESG因素以及双层决策机制,且2015—2021年间的实证结果表明由该模型得到的绿色投资组合在回测中各项指标突出,从而为绿色金融产品的构建提供了一套行之有效的解决方案。机构投资者可以应用本文所提出的绿色双层投资组合模型反向推测市场上公开交易指数的ESG偏好系数,进而刻画指数的ESG情绪变化,对基准指数绿化程度进行横向和纵向的总体评估,进而为绿色投资决策提供量化依据。此外,机构投资者可以应用本文所提出的绿色双层投资组合模型来构造绿色指数型基金,有效避免复杂的参数决策过程,并根据具体的资金募集规模、运营能力等现实约束进行差异化调整,从而服务于当前日益旺盛和多样的绿色投资需求。 未来研究包括以下几个方面:首先,本模型的上层目标实质上是有效组合和基准的马氏距离,在接下来的研究中可以引入其他测度来度量组合和基准的相似性。此外在下层问题中,可以考虑更一般的绿色投资组合模型,将待估参数集合推广至更一般的情况。在求解算法层面,精确算法在大规模问题上力有未逮,而金融市场的待选资产通常是以千计的,在后续工作中可以引入人工智能算法,如遗传算法、粒子群算法等为该问题设计大规模全局优化算法。四、实证研究
(一)数据及评价准则
(二)两类参数估计



(三)应用1:指数的ESG偏好及风险厌恶

(四)应用2:绿色型指数基金

五、结 论

