经济政策不确定性对中国股市波动率的影响
邢艳春,廖 晗
(吉林财经大学 统计学院,吉林 长春 130117)
一、引 言
金融市场的表现并不能总是与有效市场理论一致,波动最剧烈的股票市场尤为显著。中国股市出现大幅波动时,政府会及时调整或推出政策以干预股市走向,故中国股市时常被称为“政策驱动型市场”。因此,政策变动必然会对中国股市波动率产生一定影响,同时衍生出经济政策不确定性这种不能被直接或预期观测到的特性,这使得经济政策不确定性正逐渐成为市场关注重点。研究经济政策不确定性与股市波动率的影响对于探索股市异常波动原因以及预测股市波动提供了很大帮助,同时也为广大投资者以及政策制定者提供新视角。
经济政策不确定性影响研究是宏观经济研究领域的重要关注点之一。Baker等提出了经济政策不确定性指数(EPU),而后香港浸会大学Huang等编制了中国经济政策不确定性指数及其细化指数,该指数选取中国权威报纸并且利用114份报纸的数据进行了稳健性检验,其较Baker等构建的中国政策不确定性指数更具代表性和稳健性[1-2]。量化工作得到一定进展后,国内外的研究者对经济政策不确定性与股市波动关系的研究增加。在众多关系研究模型中,VAR框架和GARCH-MIDAS框架类模型最为主流。VAR类模型主要是使用低频数据,通过分时段进行脉冲响应分析经济政策不确定性对股市波动率影响效应。李成等构建了AB-SVAR模型,发现货币政策不确定性增长不利于经济的平稳增长,并且其不仅在短期内影响显著,在中长期也有显著体现[3]。陈乐一和杨依筠利用TVAR模型验证得出经济政策不确定性在常规经济增长环境下会对投资者情绪和股票价格产生负面影响[4]。
由于低频模型使用数据的限制,会将高频数据转换为低频数据,从而会损失一定的样本有效信息,故国内外学者开始研究并使用将低频和高频数据结合的混频模型。首先是Engle和Rangel等提出了将条件方差分解为短期和长期分量的乘数分量模型,此后Engle等结合Ghysels等提出的混频数据抽样模型(MIDAS)结构以及乘数模型构建了GARCH-MIDAS混频模型[5-7]。围绕着GARCH-MIDAS框架模型的改进研究越来越多,Borup和Jakobsen结合Hansen和Huang提出的REGARCH模型构建了REGARCH-MIDAS模型[8-9],随后Wu和Xie发现新息分布事实上更接近Gram-Charlier分布,结合Wu等构建的REGARCH SK模型衍生构建了REGARCH-MIDAS SK模型,提高了现有混频模型的预测精度[10-11]。由于模型的拟合效果和预测精度不断精进,国内外使用该类模型进行的宏观经济相关研究越来越多,其中不乏经济政策不确定性对股市的影响效应研究,游士兵和吴欢喜采用GARCH-MIDAS模型分析不同层面的政策不确定性对中国股市的影响,发现中国股市只受本国政策不确定性的影响[12]。如夏婷和闻岳春也利用GARCH-MIDAS模型发现货币政策和经济政策不确定性对B股的长期波动趋势有显著影响[13]。Yu和Huang将经济政策不确定性分解为水平和波动部分构建多因子GARCH-MIDAS模型,发现其能提供超出实际波动率的有用信息[14]。王莉莉采用了REGARCH-MIDAS模型发现经济政策不确定性对股市长期波动影响显著[15]。上述研究均验证了总体经济政策不确定性在一定程度上会对股市波动产生促进效应,对股市稳定发展有着阻碍作用。
基于以上分析,笔者发现国内鲜有利用REGARCH-MIDAS SK模型框架拟合股市波动率的研究,并且发现分析不同经济政策不确定性对股市波动率影响机理的研究也很少。因此,本文将以Wu和Xie提出的REGARCH-MIDAS SK模型为基础[10],引入中国经济政策不确定性指数(CEPU)构建REGARCH-MIDAS-CEPU SK双因素模型,与现有双因素模型进行拟合效果和预测精度对比,最后为了进行经济政策不确定性全面分析以及模型实际应用效果的探究,将CEPU细化指数引入该模型,以此研究中国各类经济政策不确定性与中国股市波动率的影响效应和作用机理。
二、REGARCH-MIDAS-CEPU SK模型
(一)REGARCH-MIDAS模型
Borup和Jakobsen提出的REGARCH-MIDAS模型是本文构建模型的框架基础,该模型能够有效表达波动率的杠杆效应和高持续性,且利用MIDAS技术将低频数据引入高频分析模型中,使得模型能够利用低频数据对高频数据进行更精准的分析与预测,该模型具体表达形式如下[8]:
(1)
ht=τtgt
(2)
logxt=ξ+φloght+v(zt)+ut
(3)
loggt=βloggt-1+δ(zt-1)+γut-1
(4)
(5)
其中rt为股票t日收益率,μ为股票收益率的条件均值,zt为t时刻的股票收益率新息,xt为已实现测度,为了对日内波动率更好地估计,本文采用Parzen已实现核估计值作为已实现测度的代理变量。ht为条件方差,根据乘数模型将ht分解为短期波动gt和长期成分τt两部分,其中gt使用REGARCH框架刻画,τt基于MIDAS模型构成,RV是已实现波动率,在多数研究中τt的权重梯度函数多使用Beta权重函数,具体形式为:
(6)
其中K是MIDAS模型的滞后阶数,为了保证滞后变量权重呈衰减形式,此处将ω1视为1,简化后的Beta权重函数为:
(7)
此外相较于GARCH模型,该模型方程(3)、(4)中添加了杠杆函数以捕捉股票数据的杠杆效应,其成立条件为E[δ(zt)]=0,E[v(zt)]=0,其中杠杆函数δ(zt-1)和v(zt)具体展开公式为:
(8)
(9)
由上文可知股票收益率分布通常表现为尖峰厚尾,且往往表现出时变特性,因此本文为解决时变的高阶矩问题,选择使用的高阶矩结构为:
st=ρ1+ρ2st-1+ρ3zt-1
(10)
kt=λ1+λ2kt-1+λ3|zt-1|
(11)
方程(1)~(11)定义了REGARCH-MIDAS SK模型基本框架,其中新息zt服从分布D(0,1,st,kt),偏度st和峰度kt都基于GARCH(1,1)结构形成,并有条件地依赖于收益率新息zt历史值,故zt的概率密度函数可表示为:
(12)
其中,φ(zt)服从标准正态分布。zt概率密度函数方程中的ψ(zt)与Γt展开公式如下:
(13)
(14)
由上述ψ(zt)的密度函数可知,当st=0以及kt=3时,ψ(zt)服从标准正态分布。以上方程(1)~(14)构成了REGARCH-MIDAS SK模型,其中式(1)~(5)分别为条件均值方程、测度方程、条件方差短期波动条件和方差长期成分方程,条件均值方程反映了股市收益率与其扰动项的关系,测度方程将以实现测度与条件方差进行结合联系,条件方差短期波动方程刻画了股市波动率的短期波动成分,条件方差长期成分方程结合低频数据刻画了股市波动率的长期波动成分。
(二)REGARCH-MIDAS-CEPU SK模型构建
为了研究中国各类经济政策不确定性对中国股市波动率的影响,本文在方程(5)中增加一项政策不确定性月度数据的MIDAS过程,构成了双因素REGARCH-MIDAS-CEPU SK模型的长期成分方程,其表示为:
(15)
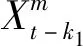
方程(1)~(4)和式(6)~(15)构成了REGARCH-MIDAS-CEPU SK模型,该模型可直接通过极大似然估计方法进行参数估计,其对数似然函数可以写为:
(16)
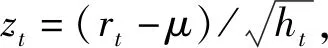
三、实证结果
(一)数据选择及描述
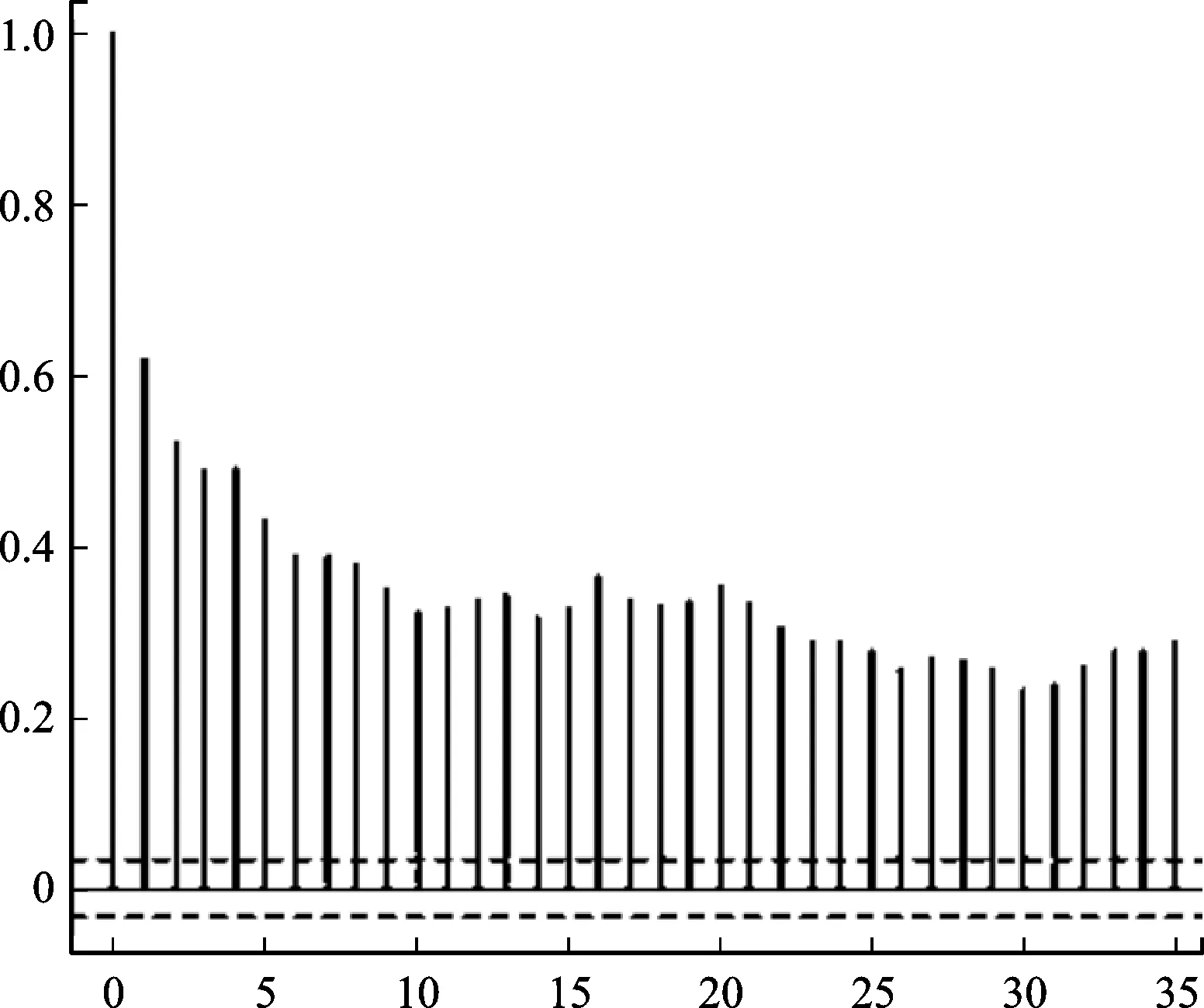
图1 RK自相关图
本文基于REGARCH-MIDAS-CEPU SK模型研究各类经济政策不确定性对中国股市波动率的影响及预测作用。实证分析部分将采用上证综指收盘价和中国经济政策不确定性细分指数,其中上证收盘价数据选取范围为2006年1月5日到2021年4月30日,共3 722个交易日数据,数据来源于Oxford-Man机构的“realised library” (https:∥realized.oxford-man.ox.ac.uk),而后对上证综指的日度收盘价进行对数化一阶差分处理,得到股市收益率(rt)数据。中国经济政策不确定性细分指数来源于Huang等的研究,抽样阶段选取为2006年1月到2021年4月,共184个月度数据[2]。已实现测度代理变量为Barndorff-Nielsen等基于5分钟已实现波动率得到的Parzen_rk数据,数据来源于Oxford-Man机构[16]。
图1为RK自相关图,可看出其以很缓慢的速度衰减,由此说明波动率具有高持续性,解决该问题需要使用REGARCH模型框架[7]。
表1为各变量描述性统计结果,股票收益率序列(rt)的偏度为-0.651 63,峰度为7.725 36,说明序列分布具有明显的尖峰厚尾特征,初步判断序列不服从正态分布,并从JB检验结果可证明rt序列不服从正态分布,即使用正态分布拟合新息分布并不准确,故本文假定新息服从Gram-Charlier分布。
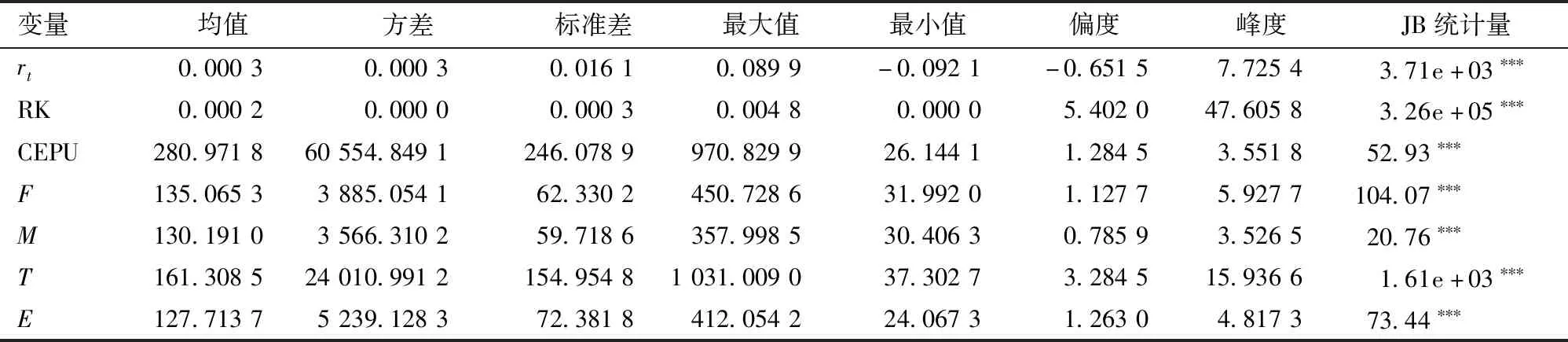
表1 各变量描述性统计
图2和图3分别为中国经济政策不确定性指数和四类政策不确定性指数时序图,图2和图3中数据来源于Huang等人研究成果[2],由图1可以看到共有三个剧烈波动时段,分别是2008年左右、2015—2017年和2019年至今。2008年的金融危机席卷全球,全球性经济动荡对中国经济造成了巨大的影响,而后中国实行了“双松”的财政和货币政策,财政和货币政策不确定性上升,也带动了中国经济政策不确定性上升。而2013年提出了“稳中求进”并将其作为今后中国经济发展主题,因此2013年后财政政策和货币政策趋于稳健,从而致使总体经济政策不确定性保持较为稳定趋势,此外观察财政政策和货币政策不确定性曲线的变动趋势,不难发现两者具有一定的同步性。2015年的“811汇改”使人民币波动摆脱受单一美元汇率影响,同时引起人民币汇率大幅波动,使得外汇和资本账户政策不确定性曲线在2015年后发生剧烈变动,使得总体经济政策不确定性随之上升。波动最为剧烈的时段为2019年至今,其中很大一部分原因是受中美贸易摩擦影响,美方贸易政策变动频繁致使中国贸易政策调整推新频次增加,使得贸易不确定性指数陡增并一直处于剧烈波动状态,从而带动了总体经济政策不确定性产生剧烈浮动。综上所述,Huang等构建的经济政策不确定性指数能及时捕捉政策变动情况,可为下文分析提供支撑[2]。
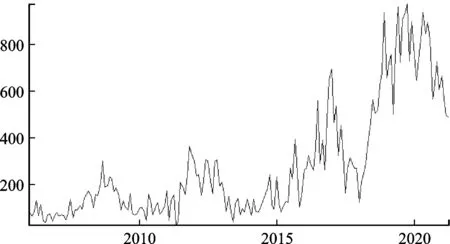
图2 中国经济政策不确定性时序图
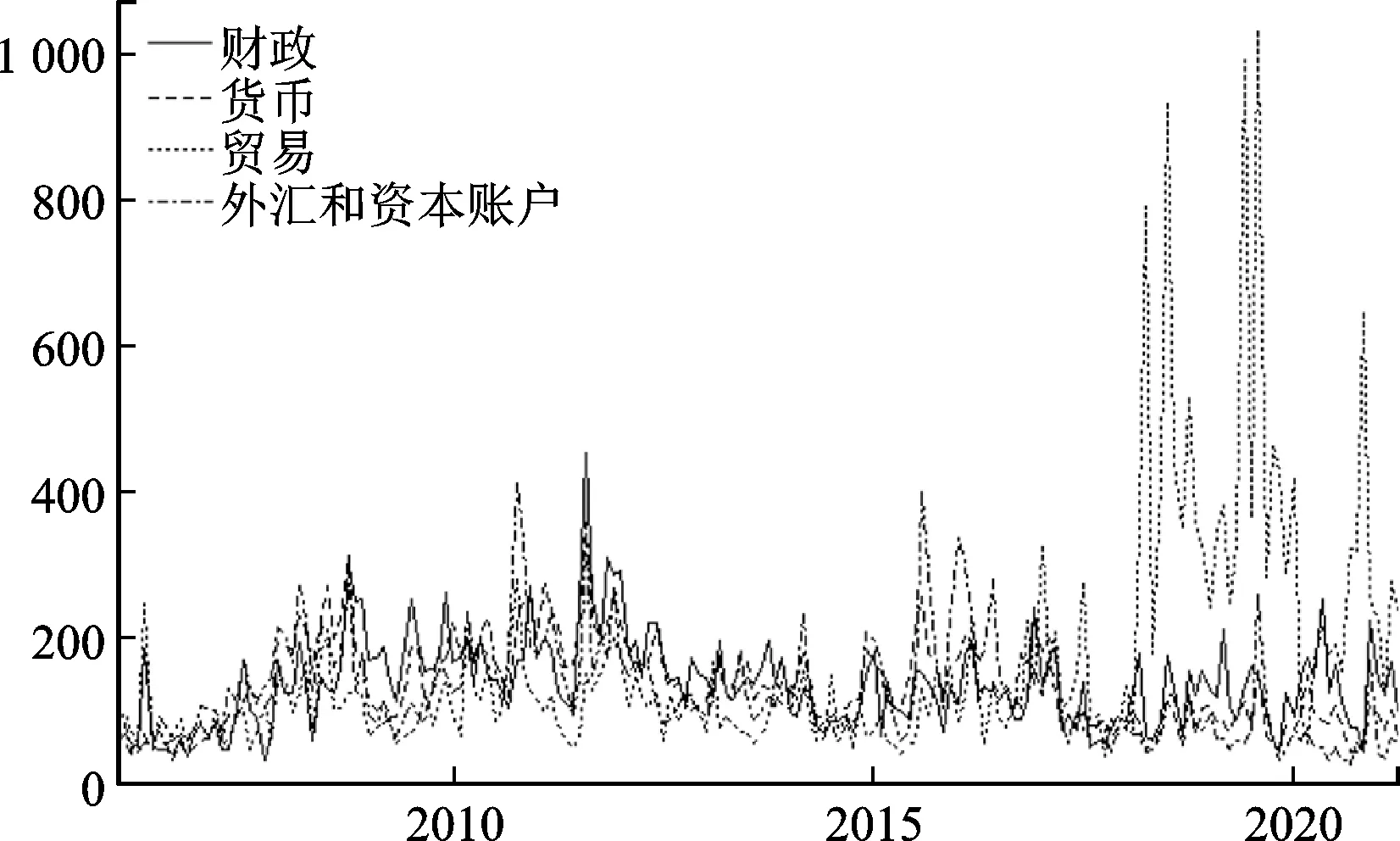
图3 各类经济政策不确定性时序图
(二)实证结果
1.引入中国整体经济政策不确定性的双因素模型
REGARCH-MIDAS SK模型是Wu和Xie在REGARCH-MIDAS模型基础上构建的,其研究证明新息分布中加入时变峰度和偏度能有效提高预测精度[10]。但单一因素模型只考虑了单个已实现波动率变量对股市波动率的影响,并未考虑对股市波动率有长期影响的其他变量,为了避免忽视长期影响因素产生的模型误设问题,本文将经济政策不确定性指数作为长期因素变量引入其中构建REGARCH-MIDAS-CEPU SK模型,并利用该模型研究各类经济政策不确定性对股市波动率的影响机理。
一是提供可以直接服务于教学、科研过程的知识传播学习与互动共享空间,比如各实习基地、教学实践课堂、创新团队的构建等;
为了验证该模型的拟合效果较已有双因素模型有所提升,本文选取了前人构建的GARCH-MIDAS-CEPU以及REGARCH -MIDAS-CEPU两种双因素模型作为对比验证模型,研究模型拟合改进情况[14-15]。
表2为模型参数估计结果。所有模型β值的估计结果均显著,并且估计值接近于1,满足β<1的约束条件,说明模型具有平稳性且波动率趋于收敛,同时也表明上证综指的波动率具有较高的持续性。δ1、δ2、v1、v2显著不为零,并且δ1和v1都为负,说明上证综指波动率具有杠杆效应。其中,θ1参数估计结果均显著为正,可得政策不确定性对股市波动具有一定的促进作用,这符合当今股票市场的经济规律[17]。
REGARCH-MIDAS-CEPU SK模型的滞后偏态参数ρ2、偏度冲击参数ρ3、滞后峰度参数λ2和峰度冲击参数λ3均为正值,其中偏态参数ρ2、偏度冲击参数ρ3显著为正,这说明收益率数据的偏态及峰度能够被模型识别并处理,证明引入SK结构有效。另外从似然值、AIC和BIC的估计结果可知,REGARCH-MIDAS-CEPU SK模型的似然值较其他两个模型大,并且AIC和BIC值较其他两个模型小,这说明该双因素模型的拟合效果较好,说明考虑了股市波动各项特性所构建的模型更加符合实际股市波动情况。

表2 GARCH-MIDAS类双因素模型拟合结果
2.双因素模型样本外预测与MCS检验结果
基于上述参数估计结果可知,本文构建的双因素REGARCH-MIDAS-CEPU SK模型拟合效果较好,为了考察该模型是否能够提高预测精度,需对上文的双因素模型进行样本外预测以及MCS检验。
本文选择向前一步滚动时间窗预测技术对股市波动率进行样本外预测[10],其中样本内预测区间为2006年1月5日到2018年12月31日共3 156个日交易数据,样本外预测区间为2019年1月2日到2021年4月30日共566个日交易数据,滚动时间窗步长为K=1。由于波动率真实值不能被直接观测,故使用已实现核估计值(RK)作为波动率的代理变量。
估计前先根据Hansen和Lunde处理方法对波动率代理变量数据进行处理[17],使其波动率代理变量值更近似于实际波动率数值,提高样本外预测准确性,计算公式为:
(17)
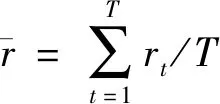
(18)
(19)
(20)
(21)
(22)
(23)
由表3的MCS检验结果可知,REGARCH-MIDAS-CEPU SK模型在六类损失函数的MCS检验中没有被剔除,并且获得了较高的MCS检验P-value(P=1),这也说明该模型的样本外预测效果稍高于其他双因素模型。
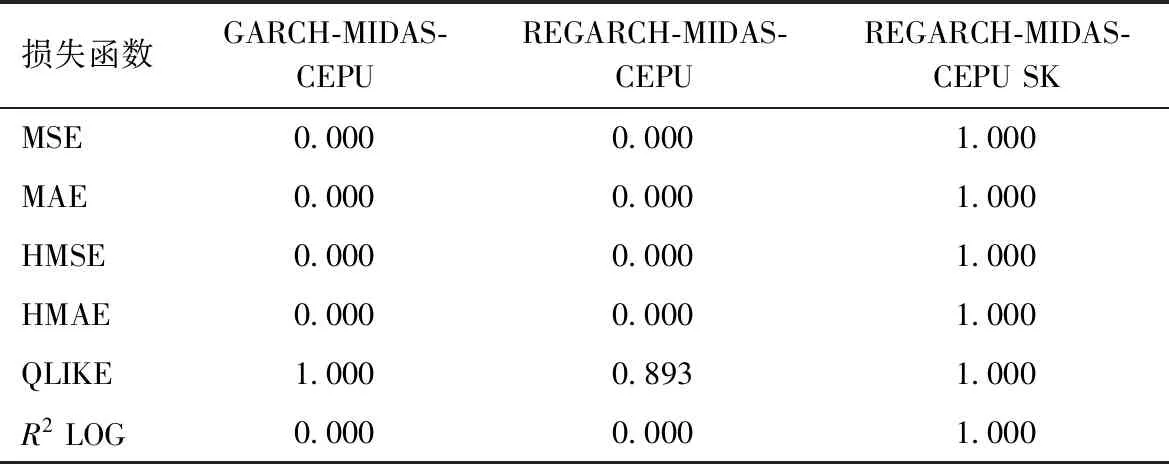
表3 MCS检验结果
(三)引入各类经济政策不确定性的双因素模型
由上文估计与检验结果可知,REGARCH-MIDAS-CEPU SK模型在研究经济政策不确定性对股市波动的影响的GARCH-MIDAS类双因素模型中,其拟合效果与预测精度都较现有双因素模型有一定提升。中国经济政策不确定性指数由多种政策不确定性综合得来,且各类经济政策不确定性的波动情况和所含信息各不相同,因此研究不同经济政策不确定性对股市波动的影响情况具有重要现实意义。故本文应用前文所构建的REGARCH-MIDAS-CEPU SK双因素模型对该问题进行研究,深入了解各类经济政策不确定性对股市波动率的影响机理。在此模型基础上将中国经济政策不确定性替换为各类政策不确定性指数构建双因素REGARCH-MIDAS-X SK模型,探究其拟合效果和不同经济政策不确定性对股市波动率的影响情况。
表4为各类经济政策不确定性双因素模型参数估计结果,可结合表2中引入中国经济政策不确定性的三种双因素模型的拟合结果分析,引入财政政策和贸易政策不确定性的双因素模型在拟合效果上依旧有所提高,以引入财政政策不确定性的双因素模型的条件方差拟合图(图4)为例,可知该模型的长期拟合值基本贴合条件方差涨幅趋势,并且能较好地捕捉股市波动长期成分。
同时从估计结果中可知四个模型的θ1参数估计结果均为正,且除了REGARCH-MIDAS-F SK模型的θ1估计值不显著外,其他三个模型均显著,财政政策不确定性模型的系数为0.042,货币政策不确定性模型的系数为0.514,贸易政策不确定性模型的系数为1.185,外汇和资本账户不确定指数模型的系数为0.267,可得各类政策不确定性都对股市波动率的波动都有一定促进作用,但每种政策对股市波动率的影响程度并不相同,其中货币政策和贸易政策不确定性对股市波动的影响程度稍大[15]。通过以上四个模型的Beta权重衰减图(图5)可知,各类经济政策不确定性对长期波动趋势的影响存在一定差异性。其中财政政策不确定性Beta权重曲线的斜率最大,说明该政策不确定性的冲击对股市波动率的长期成分的影响时间能够持续8个月左右,货币政策与外汇和资本账户政策不确定性的冲击对股市波动率的长期成分的影响时间在25个月左右,而贸易政策不确定性的衰减速度缓慢,持续时间在四类政策不确定性中最长,并且至36个月其影响还没有明显下降趋势,这证明贸易政策不确定性对股市波动率影响的时间较长。
股市波动对四类经济政策不确定性敏感程度由四类经济政策不确定性模型的权重参数ω1的估计值知晓,估计值分别为21.980、3.739、1.155和5.083,模型的估计值并不趋近,即股市波动率对四类政策的敏感变动程度不尽相同,其中财政以及外汇和资本账户政策的估计值较高,可知这两类政策不确定性发生变动引起股市出现波动的速度更快。
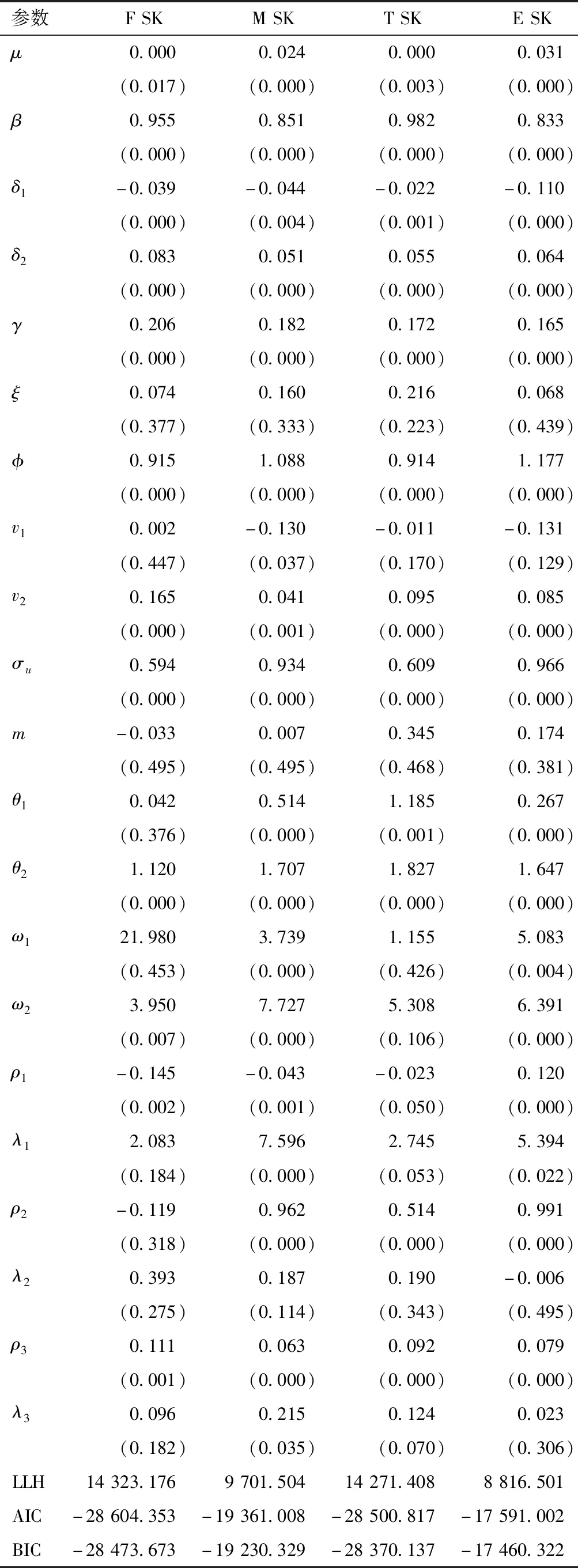
表4 各类经济政策不确定性双因素模型估计结果
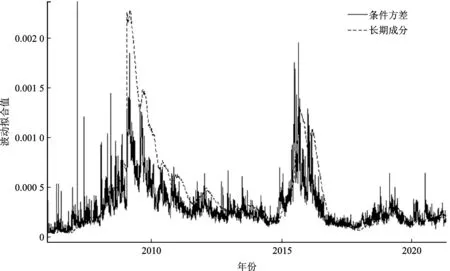
图4 REGARCH-MIDAS-F SK模型的条件方差与长期成分拟合时序图
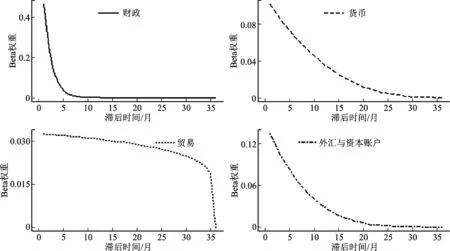
图5 Beta权重衰减图
四、结 论
本文在Wu和Xie所构建的REGARCH-MIDAS SK模型的基础上引入经济政策不确定性,提出了双因素REGARCH-MIDAS-CEPU SK模型,并将其运用于各类经济政策不确定性对股市波动的影响研究当中[10]。本文选取上证综指开盘价作为中国股市收益代理变量,中国经济政策不确定性指数及其细分指数来源于Huang等的研究,细分指数分别为财政政策、货币政策、贸易政策、外汇和资本账户四类政策不确定性指数[2]。
在此基础之上,首先将本文构建双因素REGARCH-MIDAS-CEPU SK模型与前人构建的GARCH-MIDAS-CEPU和REGARCH-MIDAS-CEPU模型进行拟合效果和预测精度对比,实证证明本文构建的双因素模型的性能较高。为了全面分析经济政策不确定性以及探究模型实际应用效果,将经济政策不确定性指数细化的四类政策不确定性指数引入构建的模型中,实证分析可得财政政策、货币政策、贸易政策、外汇和资本账户政策不确定性对股市波动均有促进作用,即不确定性水平越高股市的波动越大,这意味着不确定性的发生不利于股市保持稳定状态。影响程度方面,货币政策和贸易政策不确定性对股市波动的影响较大,财政政策与外汇和资本账户政策次之;影响持续时间方面,贸易政策不确定性对股市波动率的影响持续时间较长,货币政策与外汇和资本账户政策次之。股市波动敏感程度方面,在同等条件下,股市波动率对四类政策不确定性的敏感程度并不相同,其中对财政政策以及外汇和资本账户政策不确定性变动的敏感程度较高。
本研究为经济政策不确定性及细化政策不确定性对股市波动率的影响研究提供了更准确的理论与方法借鉴,明晰了各类经济政策不确定性对股市波动率的影响大小、持续情况以及敏感程度,对于学术研究、实际工作者和股市投资者都具有重要意义。值得一提的是,本文的研究工作还有一定的进步空间,比如各类经济政策不确定性对债券、期货市场波动影响分析,或探究各类经济政策不确定性及其他相关因素是否会在三大金融市场中有相关联动效应等等,今后将对以上问题重点关注并进行相关研究。

