基于新型滑模趋近律的风机类负载永磁同步电机控制研究

单军宝，王汉文，张 兴，贾 铭，周堂鑫，何微波

（1.安徽省电机产品及零部件质量监督检验中心，安徽 宣城 242500；2.安徽工业大学电气与信息工程学院，安徽 马鞍山 243002）

目前中国对于电机用量比较大的几种机械设备分别是压缩机、水泵、风机、搅拌机、机床等[1]。其中风机负载用电量在中国工业用电中占了很大的份额。传统的电机驱动风机负载，采用阀门控制或者挡板控制的方式来调节风量，这种方法会在管道上消耗大量的能量，会使系统效率低[2-4]。随着目前社会对于节能和高效率的要求，对于风机负载的驱动多采用功率密度高、速度稳定性强、高转矩惯性比的永磁同步电机。

风机应用场合十分广泛，常见的风机有2种，即离心式风机和轴流式风机。风机常见的应用领域有通风换气、锅炉、矿井、输送热带站煤粉、工业炉等，根据应用场合的不同，其风机的尺寸和规格也有所不同[5]。

工业炉风机的作用是连续不断地提供燃料燃烧所需的氧气，并及时将锅炉燃烧的烟气排除。这就需要风机能够提供稳定的风速和风量，从而能够满足工业锅炉对于风机的要求。风机能否可靠地运行，会直接影响工业炉的运行性能。

在风叶确定的情况下，风量是以稳定的转速来维持的，这就要求电机能为风机提供稳定的转速。工业炉风机运行期间，主要是为工业炉提供风力，若工业炉的风机不能及时达到给定转速，会造成风量偏小，从而使燃烧室缺氧，导致燃烧效率低下，降低了锅炉的效率，直接影响锅炉的产热量，因此电机转速还应具备良好的跟随性和快速性[6]。

为此本文提出了一种全新的趋近律滑模控制SMC（Sliding Mode Control）控制算法，在原指数趋近律的基础上，为能更好地实现速度跟随，加快系统的响应速度，将传统控制算法中的切换函数用终端吸引子来取代，并且使终端吸引子与控制系统中状态量的幂函数相关联，能够更好地提高对系统的控制能力，将此趋近律运用在系统的转速环中，并将传统的PI控制结果和传统滑膜控制方法进行了对比分析。

1 电机及风机类负载建模

为了便于控制器的设计，采用id=0的控制方式，建立d-q坐标系下的表贴式PMSM（Permanent Magent Synchoronous Motor）电机数学模型，公式为：

式（1）中：iq为q轴上的定子电流；Ls为定子电感；R为定子电阻；Pn为极对数；φf为磁链；wm为电机角速度；uq为q轴上的定子电压；J为转动惯量；TL为负载转矩。

风机依靠电机输入的机械能，将气体的压力提高后将其排出。因此风机是一种从动的用于气体输送的流体机械。在一定转速范围内，风机类负载的输出转矩TL是一种变负载转矩，其与转速的平方成正比[7-8]，即：

式（2）中：C是常数，根据负载的情况而定。

2 新型趋近律设计

2.1 传统指数趋近律

典型的指数趋近律为：

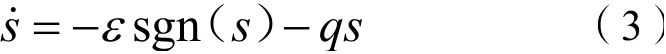
由式（3）可以看出，典型指数趋近律是由等速趋近环节和指数环节组成。可以通过控制ε和q来降低抖振状态并提高对系统的趋近速度，但是当增大q时，通常也必须降低ε，要不然会使系统的抖振增大，因此需要设计合理的ε和q值。

2.2 终端吸引子

为了能够得到更好的控制效果，本文引入了终端吸引子来替代原本的sgn（s）函数，利用终端吸引子能够在滑模面附近快速收敛的特性，使系统能够在有限时间内快速收敛到平衡点，来改善系统的控制品质[9]。

终端吸引子基本表达式为：

式（4）中：x为系统的状态变量；p、q为自定义参数。

2.3 新型趋近律的设计

为克服传统控制算法的缺点，本文在引入终端吸引子的情况下设计了一种新型的趋近律，新型趋近律为：式（5）（6）中：k1、k2、k3、m、n、q、p、a、d为自定义参数，k1、k2、k3均大于0，m、n也大于0，p＞q＞0（且p和q均为正奇数），a、d均大于0小于1。

图1 μ函数结构图

2.4 稳定性分析

为证明本文中所提出趋近律的稳定性，定义李雅普诺夫函数为：对式（7）求导得：

因此当S不为0时，；当S=0时，满足李雅普诺夫判稳条件因此该趋近律存在且稳定。

2.5 滑模控制器的设计

定义永磁同步电机的状态变量为：

式（9）中：wref为电机的参考转速；wm为电机实际的转速。

从式（1）和式（9）可以得到：

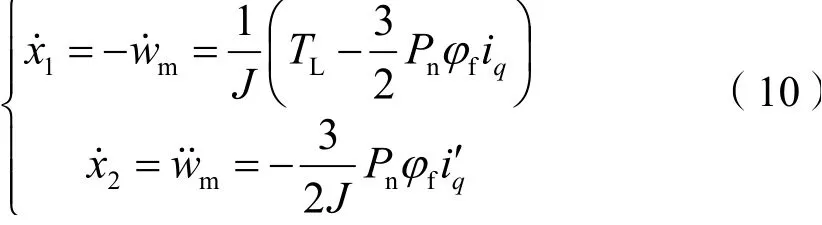
将式（10）中的iq′定义为u，定义为D，此时定义滑模面为：

对式（11）进行求导可得：

将式（5）和式（6）代入式（12）可得控制器的表达式为：

由式（13）可得滑模环的输出电流为：

2.6 抗积分饱和器设计

系统中滑膜输出值是送给电流环的，对电机来说，当电流值超过电机的承受能力时，会使电机遭受一定的损坏，会使系统出现较大的超调。因此，有必要在系统的滑模环中设置一定的抗积分饱和处理措施，这样系统能够得到良好的结果[10]。对此，本文在滑模控制环节引入了一种抗积分饱和方案，其具体函数表达式为：

此时可得到滑模环输出的电流为：

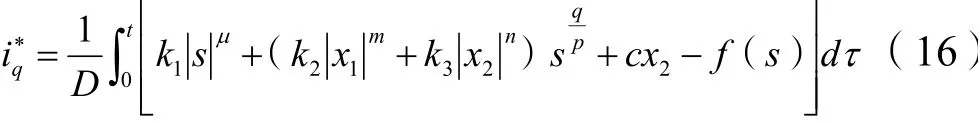
3 仿真及结果分析

3.1 仿真模型的搭建

在Matlab/Simulink中搭建仿真模型，其中改进的趋近律各参数选取为a=0.001，d=0.1，p=7，q=5，c=100，k1=100，k2=4 000，k3=100，k4=5 000，m=0.05，n=0.2。永磁同步电机新型滑膜调速控制框图如图2所示。

图2 基于新型滑模的PMSM矢量控制框图

在Simulink中将直流侧电压输出设置成311 V，仿真时间为1 s，电机初始给定转速设置为200 r/min，0.5 s时将转速从200 r/min变到300 r/min，并将风机类负载的常数C根据实际负载设置为5×10-6。

电机参数设置如表1所示。

表1 PMSM参数

表1 （续）

3.2 仿真结果分析

为验证本文所提新型滑模趋近律算法能够满足工业炉对于风机快速达到稳定转速的要求，故对转速、输出转矩和A相定子电流仿真波形进行分析。

图3为永磁同步电机转速突变波形图。从图中可以看出，与传统的指数趋近律控制和传统的PI转速控制相比，新型趋近律控制能够更好地削弱系统抖振，且达到稳定的时间更短，在启动阶段PI控制算法的转速达到225 r/min，有25 r/min的超调，超调率达到12.5%，转速突变时有5 r/min的超调，超调率为2.5%，而新型趋近律无超调现象。传统的趋近律控制算法虽没有超调现象，但趋于稳定时间比新型趋近律慢了0.05 s。新型趋近律稳定后的波动范围为199.9～200.1 r/min，传统PI控制算法稳定后的波动范围为199.65～200.35 r/min，传统趋近律稳定后的波动范围为199.7～200.3 r/min。相比于另外2种传统方法，新型趋近律在稳定后的波动范围比传统PI少了0.5 r/min，比传统趋近律少了0.4 r/min，因此可得出新型趋近律控制精度更高，响应速度更快。

图3 电机转速对比波形图

图4为在3种控制方法下的电机转矩波形图。从图中可以看出，基于本文所提的新型趋近律控制下的效果较其他2种控制动态性能更好，系统能够迅速地跟随指定转矩，且在转矩发生突变时，波形更加平滑，启动瞬间超调更小。

图4 电机转矩对比波形图

图5为3种控制方法下的电机A相电流对比波形图。从图中可以看出，基于新型趋近律控制下的A相电流谐波更小，波形更加平滑，且在电机启动瞬间和电流发生变化时，波形稳定性更好，电流谐波降低，使无功损耗降低，从而能够减少控制系统的能量损耗，可以达到节能的目的。

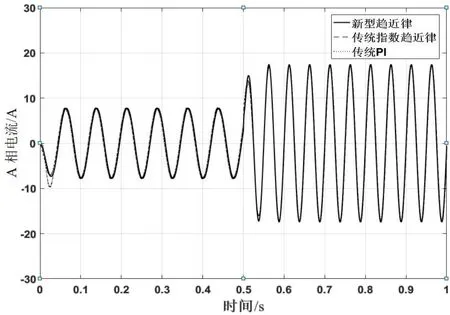
图5 A相电流对比波形图

综上可得，本文设计的新型趋近律控制算法更优，控制系统的响应速度更快，控制精度更高，系统动态性能更好，能够满足工业炉对于风机的要求。

4 结论

为满足工业炉对于风机快速稳定转速的要求，本文设计了一种新型的滑模趋近律函数。通过Matlab/Simulink仿真结果即可得出，新型趋近律相比于传统的PI控制算法和传统的滑模控制算法能够更好地减小超调、削弱抖振，响应速度更快，动、静态性能更好，跟踪性能更优。且与传统的控制算法相比，电流谐波含量的降低可以减少损耗、提高效率。这些优点使其能够满足工业炉对于风机的要求。